hi, pls help.
Why do Jews consider the Western Wall in Jerusalem a sacred place? *
1. It was built by King Solomon.
2. It was all that was left of the Second Temple after the Romans destroyed it.
3. It was the place where Abraham settled.
4. It was constructed with the stones that held the Ten Commandments.

Answers
Answer:
Hope that helps
Step-by-step explanation:
It was constructed with the stones that held the Ten Commandments.
Answer:
all that was left of the second temple after the roans destroyed it
Step-by-step explanation:
Related Questions
What is the value of c in the equation below?
2 Superscript negative 4 Baseline times 2 squared = a Superscript b Baseline = c
Answers
Answer:
c
Step-by-step explanation:
Answer:
1/4
Step-by-step explanation:
If a + b= 29, b + c = 45, a + c = 44
Find a + b + c = ?
Answers
Answer:
a+b+c=59
Step-by-step explanation:
a+b=29
b+c=45
a+c=44
Therefore we know that a and b are each equal to less than 29. And c must be equal to less than 44. By messing around with those numbers I got that if a is equal to 14 and b is equal to 15, that gives us 29. And if b is equal to 15, then 15 minus 45 is equal to 30. Meaning that c would equal 30. And if we add c + a, or 30+14, that is equal to 44. So then a+b+c=? can be written as 14+15+30=59
show that a tree has at most n/2 many vertices that have degree 3 or higher
Answers
To show that a tree has at most \(n/2\)many vertices that have degree 3 or higher, we will use proof by contradiction.
Assume that there exists a tree with more than \(n/2\) vertices that have a degree of 3 or higher. Let V be the set of vertices in the tree, and let \(V_3\) be the set of vertices in V that have a degree 3 or higher. Let k be the number of vertices in\(V_3.\)
Since the tree has n vertices, there are n-k vertices in V that have degree 1 or 2. Since each vertex in the tree has degree at least 1, we have \(n-k ≤ n\), which implies that k ≥ 0.
Now, consider the sum of degrees of all vertices in the tree. By definition of a tree, this sum is twice the number of edges in the tree, which is n-1. Therefore, we have:
\(2(n-1) = Σ_degrees\)
where \(Σ_degrees\) is the sum of degrees of all vertices in the tree.
Let d_i be the degree of the i-th vertex in V_3. Since each vertex in V_3 has degree 3 or higher, we have d_i ≥ 3 for all i. Therefore, the sum of degrees of vertices in V_3 is at least 3k.
Let m be the number of vertices in V that have degree 1 or 2. Let d_j be the degree of the j-th vertex in V that has degree 1 or 2. Since each vertex in V that has degree 1 or 2 has degree at most 2, we have d_j ≤ 2 for all j. Therefore, the sum of degrees of vertices in V that have degree 1 or 2 is at most 2m.
Since V is the disjoint union of \(V_3\) and the set of vertices in V that have degree 1 or 2, we have:
\(Σ_degrees = Σ_{i=1}^k d_i + Σ_{j=1}^m d_j\)
Combining the inequalities \(3k ≤ Σ_{i=1}^k d_i and Σ_{j=1}^m d_j ≤ 2m, we get:\\Σ_degrees ≥ 3k + Σ_{j=1}^m d_j ≥ 3k\)
where the last inequality follows from for all j.
To know more about vertices here
https://brainly.com/question/24772274
#SPJ4
Mike painted a tabletop that is shaped like a circle. The circumference of the tabletop is 8π feet. Which measurement is closest to the area of the tabletop in square feet.
Answers
A measurement that is closest to the area of the tabletop in square feet is 50 ft².
How to calculate the circumference of a circle?Mathematically, the circumference of a circle can be calculated by using this mathematical expression:
C = 2πr or C = πD
Where:
C represents the circumference of a circle.D represents the diameter of a circle.r represents the radius of a circle.Substituting the given parameters into the circumference of a circle formula, we have the following radius;
8π = 2πr
r = 8π/2π
Radius, r = 4 feet.
Mathematically, the area of a circle can be calculated by using this formula:
Area of a circle = πr²
Area of a circle = 3.14(4)²
Area of a circle = 50.24 ≈ 50 ft².
Read more on area of circle here: https://brainly.com/question/8644160
#SPJ1
Find the slope and y-internet.

Answers
Y-intercept: first one
Explanation
Slop is rise over run so how much it goes up or down on the top and how much it goes our right on the bottom
Y-intercept is where the point intersects with the y line so what point is on the y line
What is the slope of the line graphed below

Answers
Answer:
\(\frac{3}{4}\) or 0.75
Step-by-step explanation:
I apologize if I'm incorrect
help please !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!111

Answers
Jenna and Mia arrived at the same answer because both the methods they have adopted are correct.
Given solution of a question done by two people.
Jenna's method
5(30+4)
(5)(30)+(5)(4)
150+20=170
Mia's method
5(30+4)
5(34)=170
We are required to find why they have achieved at the same answer.
Jenna and Mia have achieved at the same answer because they both have adopted the right method.Jenna's method is the equation in its simplest form. Addition of that is easily understood. While Mia's method is just valid as Jenna's some people may have trouble remembering the steps of multiplication within parantheses as well as being able to look at large multiplication problem and automatically knowing the answer or being able to get the answer as fast as simple addition.
Hence Jenna and Mia arrived at the same answer because both the methods they have adopted are correct.
Learn more about multiplication at https://brainly.com/question/10873737
#SPJ1
Can someone please tell me if the following relations are functions please?

Answers
the slope of the simple linear regression equation represents the average change in the value of the dependent variable per unit change in the independent variable (x).
Answers
The slope of the simple linear regression equation represents the average change in the value of the dependent variable per unit change in the independent variable (x).
A linear regression equation is the formula for the straight line that best represents a given dataset in statistics. The equation represents the relationship between the dependent and independent variables with the help of a straight line.
It is often used to predict or forecast the dependent variable values based on the independent variable values.A slope is a measure of the steepness of the line in the linear regression equation.
It refers to the rate of change of the dependent variable concerning the independent variable.
The slope of the equation is denoted by the symbol “m”.In conclusion, the slope of the simple linear regression equation represents the average change in the value of the dependent variable per unit change in the independent variable (x).
To know more about linear regression visit:
https://brainly.com/question/30401933
#SPJ11
Solve the following inequality.
7(6 - 4n) + 4n > 138
Answers
Answer:
n <−4
42 - 28n + 4n >138
42 - 24n >138
-24n > 138 - 42
-24n >96
n <−96/24
N <−4
Can someone help me with this question?

Answers
Prove, using the definition of the derivative, that if f(x) = cos (x), then f'(x) = -sinx.
Answers
The derivative of a function represents the rate of change of the function with respect to its variable. This rate of change is described as the slope of the tangent line to the curve of the function at a specific point. The derivative of the cosine function can be found by applying the limit definition of the derivative to the cosine function.
\(f(x) = cos(x) then f'(x) = -sin(x)\).
Let's proceed with the proof. Definition of the Derivative: The derivative of a function f(x) at x is defined as the limit as h approaches zero of the difference quotient \(f(x + h) - f(x) / h\) if this limit exists. Using this definition, we can find the derivative of the cosine function as follows:
\(f(x) = cos(x) f(x + h) = cos(x + h)\)
Now, we can substitute these expressions into the difference quotient: \(f'(x) = lim h→0 [cos(x + h) - cos(x)] / h\)
We can then simplify the expression by using the trigonometric identity for the difference of two angles:
\(cos(a - b) = cos(a)cos(b) + sin(a)sin(b)\)
Applying this identity to the numerator of the difference quotient, we obtain:
\(f'(x) = lim h→0 [cos(x)cos(h) - sin(x)sin(h) - cos(x)] / h\)
We can then factor out a cos(x) term from the numerator:
\(f'(x) = lim h→0 [cos(x)(cos(h) - 1) - sin(x)sin(h)] / h\)
We can then apply the limit laws to separate the limit into two limits:
\(f'(x) = lim h→0 cos(x) [lim h→0 (cos(h) - 1) / h] - lim h→0 sin(x) [lim h→0 sin(h) / h]\)
The first limit can be evaluated using L'Hopital's rule:
\(lim h→0 (cos(h) - 1) / h = lim h→0 -sin(h) / 1 = 0\)
Therefore, the first limit becomes zero:
\(f'(x) = lim h→0 - sin(x) [lim h→0 sin(h) / h]\)
Applying L'Hopital's rule to the second limit, we obtain:
\(lim h→0 sin(h) / h = lim h→0 cos(h) / 1 = 1\)
Therefore, the second limit becomes 1:
\(f'(x) = -sin(x)\)
Thus, we have proved that if \(f(x) = cos(x), then f'(x) = -sin(x)\).
To know more about expressions visit :
https://brainly.com/question/28170201
#SPJ11
A plastic pool gets filled up with 10L of water per hour.
a) After 2 hours how much water is in the pool? Write an equation.
b) After how many hours will the pool be 80L?
c) Is part b) linear or nonlinear?
Answers
a) The amount of water in the pool after 2 hours can be calculated using the equation.
Water in pool = 10L/hour × 2 hours = 20L.
b) The pool will be 80L when the equation is satisfied: 80L = 10L/hour × Time.
Solving for Time, we find Time = 8 hours.
c) Part b) is linear.
a) To calculate the amount of water in the pool after 2 hours, we can use the equation:
Water in pool = Water filling rate × Time
Since the pool gets filled up with 10L of water per hour, we can substitute the values:
Water in pool = 10 L/hour × 2 hours = 20L
Therefore, after 2 hours, there will be 20 liters of water in the pool.
b) To determine the number of hours it takes for the pool to reach 80 liters, we can set up the equation:
Water in pool = Water filling rate × Time
We want the water in the pool to be 80 liters, so the equation becomes:
80L = 10 L/hour × Time
Dividing both sides by 10 L/hour, we get:
Time = 80L / 10 L/hour = 8 hours
Therefore, it will take 8 hours for the pool to contain 80 liters of water.
c) Part b) is linear.
The equation Water in pool = Water filling rate × Time represents a linear relationship because the amount of water in the pool increases linearly with respect to time.
Each hour, the pool fills up with a constant rate of 10 liters, leading to a proportional increase in the total volume of water in the pool.
For similar question on amount.
https://brainly.com/question/25720319
#SPJ8
A store is having a sale on jellybeans in trail mix. For 2 pounds of jellybeans and 12 pounds of trail mix, the total cost is $23. For 5 pounds of jellybeans and 3 pounds of trail mix, the total cost $17 find the cost for each pound of jellybeans in each pound of trail mix
Answers
Answer:
The jelly beans cost $2.25 / pound
The trail mix costs $1.25 / pound
Step-by-step explanation:
Let +a+ = cost/pound of jelly beans
Let +b+ = cost/pound of trail mix
(1) 6a + 2b =16
(2) 3a + 5b =13
Multiply both sides by 2
and subtract (1) from (2)
(2) 6a -2b = -16
(1) -6a -2b = -16
8b=10
b=1.25
and
(1) 6a+2b=16
(1) +3a+b=8
(1) 3a+1.25=8
(1) +3a=6.75
(1) a=2.25
read the picture plsssssssssss

Answers
2. 2x - 5(3x^2)
3. 8x + 2x/3 +6
4. x + 3 - y - 6
in which age classes do the median and quartiles fall?
Answers
The median and quartiles fall in the middle age classes.
The median is the middle value in a set of data, meaning that half of the data falls below the median and half falls above it. The quartiles divide the data into four equal parts, with the first quartile (Q1) being the 25th percentile, the second quartile (Q2) being the median or 50th percentile, and the third quartile (Q3) being the 75th percentile.
In terms of age classes, the median and quartiles would fall in the middle age classes. For example, if the age classes were 0-10, 11-20, 21-30, 31-40, 41-50, 51-60, 61-70, 71-80, and 81-90, the median and quartiles would fall in the 21-30, 31-40, and 41-50 age classes.
It is important to note that the specific age classes that the median and quartiles fall in will depend on the distribution of the data. However, they will always fall in the middle age classes, as they represent the middle values of the data set.
Know more about median here:
https://brainly.com/question/26151333
#SPJ11
A direct relationship between two variables is reflected in a(n) _____ correlation coefficient.
Answers
A direct relationship between two variables is reflected in a "POSITIVE" correlation coefficient.
Correlation is a statistical technique for measuring and describing the relationship between two variables.
The variables move in the same direction when they have a positive correlation. In other words, as one variable increases, so does the other, and conversely, as one variable decreases, so does the other.
Typically, the two variables are simply observed rather than manipulated. Two scores from the same individuals are required for the correlation.
Find more on correlation coefficient at : https://brainly.com/question/28213588
#SPJ4
which polynomial function is graphed below? A. f(x)=(x-4)(x+2)2
B. f(x)=(x+4)(x-2)2
C. f(x)=(x+4)2(x-2)
D. f(x)=(x-4)2(x+2)

Answers
Answer:
b) f(x)=(x+4)(x-2) 2.....
The zeros on the graph satisfy the function f(x)=(x+4)(x-2)². Therefore, option B is the correct answer.
In the given graph, the function is plotted.
What is the function?Functions are the fundamental part of the calculus in mathematics. The functions are the special types of relations. A function in math is visualized as a rule, which gives a unique output for every input x.
The zero of a polynomial is (2, 0) and (-4, 0)
A. f(x)=(x-4)(x+2)²
Put (2, 0) in y=(x-4)(x+2)², we get 0=(2-4)(2+2)²
LHS≠RHS
B) f(x)=(x+4)(x-2)²
Put (2, 0) in y=(x+4)(x-2)², we get 0=(2+4)(2-2)²
LHS=RHS
Put (-4, 0) in y=(x+4)(x-2)², we get 0=(-4+4)(-4-2)²
LHS=RHS
C) f(x)=(x+4)²(x-2)
Put (2, 0) in y=(x+4)²(x+2), we get 0=(2+4)²(2+2)
LHS≠RHS
D) f(x)=(x-4)²(x+2)
Put (2, 0) in y=(x-4)²(x+2), we get 0=(2-4)²(2+2)
LHS≠RHS
The zeros on the graph satisfy the function f(x)=(x+4)(x-2)². Therefore, option B is the correct answer.
To learn more about the function visit:
https://brainly.com/question/28303908.
#SPJ2
Jaime says that the value of -1 x n is always equal to the value of n divided (-1) for all values of n. Explain whether Jaime is correct or incorrect.
Answers
Answer:
James is correct.
Step-by-step explanation:
We want to see if -1*n is equivalent to n/(-1).
We will see that these operations are equivalent, so Jaime is correct.
So, let's start with the original equation:
-1*n
Notice that we can rewrite:
-1 = -1/1 = -(1/1) = 1/(-1)
Then if we write:
-1*n = (1/(-1))*n = (1*n)/(-1) = n/(-1)
So Jaime is actually correct, this happens because when we multiply or divide by -1 we do not change the value of n, we only change the sign, so these two operations are equivalent.
If you want to learn more, you can read:
https://brainly.com/question/15439350
Which expressions are equivalent to the given expression?

Answers
Answer:
(a). and (b).
Step-by-step explanation:
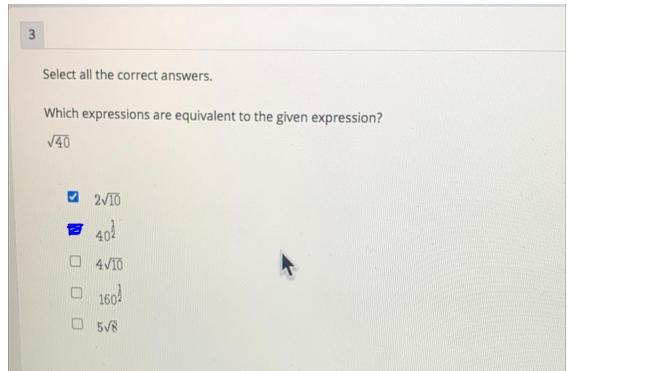
Simplify Square Roots -
Find one perfect square and one imperfect square to multiply to the square root.
\( \sqrt{4 \times 10} = 2 \sqrt{10} \)
\(40^{ \frac{1}{2} } = \sqrt[2]{(40) ^{1} } = \sqrt{40} \)
\( \sqrt{40} \neq 4 \sqrt{10} \)
\(160 ^{ \frac{1}{2} } = \sqrt[2]{160 ^{1} } = \sqrt{160} \neq \: \sqrt{40} \)
\(5 \sqrt{8} \neq \: \sqrt{40} \)
shows a two reservoir water supply system. the water level in reservoir 1 drops at thje rate of 0.01 m/min
Answers
The rate at which the water level in reservoir 1 drops can be calculated as follows:
Let the volume of reservoir 1 be V1, and the surface area be A1. The volume of water that is flowing out of reservoir 1 per minute is given by;
V = A1 x h
where h is the height of water that flows out of reservoir 1 per minute. Since the water level in reservoir 1 drops at a rate of 0.01 m/min, then the height of water that flows out of reservoir 1 per minute is 0.01 m/min. Therefore, the volume of water that flows out of reservoir 1 per minute is given by;
V = A1 x hV = A1 x 0.01 .
Assuming that the cross-sectional area of the pipe that connects the two reservoirs is the same as that of reservoir 1 (A1), then the volume of water that flows into reservoir 2 per minute is also given by;
V = A2 x h
where A2 is the surface area of reservoir 2.
Therefore, the rate at which the water level in reservoir 2 rises can be calculated as follows:
Let the volume of reservoir 2 be V2. The volume of water that flows into reservoir 2 per minute is given by;
V = A2 x hA1 x 0.01 = A2 x h = (A1 / A2) x 0.01
Since the height of water that flows out of reservoir 1 per minute is 0.01 m/min, then the height of water that flows into reservoir 2 per minute is (A1 / A2) x 0.01. Therefore, the rate at which the water level in reservoir 2 rises is given by;
(A1 / A2) x 0.01 m/min.
To view a similar solved question : https://brainly.com/question/29575599
#SPJ11
Does someone mind helping me with this? Thank you!

Answers
Answer:
Step-by-step explanation:
Just plug each value of x into the equation to get y:
f(-2) = (√-(-2) - 2) + 2 = √0 + 2 = 2
f(-3) = (√-(-3) - 2) + 2 = √1 + 2 = 3
f(-6) = (√-(-6) - 2) + 2 = √4 + 2 = 4
f(-11) = (-(-11) - 2) + 2 = √9 + 2 = 5
wich expression shows a way to factor 15+18
Answers
3(5+6) can also be written as 3 x (5+6) or in a more simpler form, 5+6= is 11. So when we multiply 11 x 3, we get 33 which is also equal to 3(5+6) = 33. Hope this helps.
Change 890cm into meters
Answers
Answer:
8.9
Step-by-step explanation:
the height of basketball players is considered a continuous variable. group of answer choices true false
Answers
TRUE: Basketball players' height is seen as a continuous variable.
Explain the term Continuous Random Variable?For any statistical researcher, the precise estimation of random variables including their classification are crucial.For instance, the type of distribution we can employ with a random variable depends on the nature of a random variable.Yes, as lengths are continuous variables, the random variable does indeed refer to length.
It should be noted that a length value may include as many decimal places is necessary without producing an error. A basketball player, for instance, can be 180 cm, 180.9 cm, or 188.99 cm tall.Thus, Basketball players' height is seen as a continuous variable
To know more about the Continuous Random Variable, here
https://brainly.com/question/17217746
#SPJ4
17. Carol and Cathy are each saving money for a vacation. Carol started with $25 and saves
$7.50 a week. Cathy started with $10 and saves $10 a week. When will they have saved
the same amount?
Answers
Answer:
6 weeks
Step-by-step explanation:
Let x represent the weeks
\(25=10+ (10x-7.5x = 2.5)\)
\(25-10=2.5x = 15\)
\(\frac{15}{2.5}=x \\(150/25)\\x=6\)
Carol and Cathy will have same saved amount after 6 weeks.
What do you mean by algebraic expressions ?
Algebraic expression is an equation which consists of variables and the arithmetic operations such as division , multiplication , etc.
It is given that Carol started with $25 and saved per week an amount of $7.50 whereas Cathy started with $10 and saved per week amount of $10.
Let's assume that after x no. of weeks they will have same saved amount.
So , we can write an algebraic expression which is :
25 + (7.5 × x) = 10 + (10 × x)
Now , reordering the like terms we get :
10x - 7.5 x = 25 - 10
Simplifying this we get :
2.5 x = 15
or
x = 15 ÷2.5
or
x = 6 weeks
Therefore , Carol and Cathy will have same saved amount after 6 weeks.
Learn more about algebraic expressions here :
brainly.com/question/27882730
#SPJ5
- 1 = 2m - n; solve for n
Answers
Answer:
n = 2m + 1
Step-by-step explanation:
\(-1=2m-n\\\\-1+n=2m-n+n\\\\-1+n=2m\\\\-1+1=n=2m+1\\\\\boxed{n=2m+1}\)
Hope this helps.
Can somone help me:)

Answers
Answer:
$6
Step-by-step explanation:
Select the expression that results in a rational number.

Answers
The correct answer is A.\(\((5 \frac{1}{\overline{9}}) \times (-0.\overline{3})\)\), as it involves the multiplication of two rational numbers, resulting in a rational number.
The expression that results in a rational number is A. \(\((5 \frac{1}{\overline{9}}) \times (-0.\overline{3})\)\). To determine if an expression yields a rational number, we need to check if it involves the multiplication of two rational numbers. In option A, \(\(5 \frac{1}{\overline{9}}\)\) represents a mixed fraction, which can be expressed as the sum of a whole number and a fraction, both of which are rational. Similarly, \(\(-0.\overline{3}\)\) is a repeating decimal, which can be expressed as a fraction, also a rational number.Therefore, the product of these two rational numbers in option A will yield a rational number.
For more questions on rational numbers:
https://brainly.com/question/19079438
#SPJ8
Find the inverse function. 1 f(x) = 1 = 2x+2 + f-1(x) = [? ]x + [
![Find the inverse function. 1 f(x) = 1 = 2x+2 + f-1(x) = [? ]x + [](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/28y81xbb988owHxSh6WATvMqEkhqDGkO.jpeg)
Answers
Answer:
y= 2x - 1
Step-by-step explanation:
i hope that helps