How do i figure out (4x -14)
Answers
Related Questions
BC is tangent to circle A. Determine the length of AC.

Answers
Answer:
5
Step-by-step explanation:
AC=√(3^2+4^2)=√(9+16)=√(25)=5
suppose p, q,and r are three independent and identically distributed poisson random variables with mean k. let w = 20p – 5q 10r. if the coefficient of variation of w is 0.8739, find k.
Answers
If the coefficient of variation of w is 0.8739, then the value of k is 1.1.
Given that, P, Q and R are three independent and identically distributed Poisson random variables with mean k.
Here,
\(E(P)=E(Q)=E(R)=k\)
\(V(P)=V(Q)=V(R)=k\)
Let \(W=20p-5Q+10R\)
\(= 20E(P)-5E(Q)+10E(R)\)
\(= 20k-5k+10k\)
\(= 25k\)
\(V(W)=V(20p-5Q+10R)\)
\(=400V(P)+25V(Q)+100V(R)\)
\(= 400k+25k+100k\)
\(= 525k\)
We know that, coefficient of variance is
\(C.V=\frac{\sigma}{\mu}\)
\(\frac{\sqrt{525k}}{25k}=0.8739\)
\(\sqrt{525k}=21.8475 k\)
\(525k = 477.313256 k^2\)
\(k=\frac{525}{477.313256}\)
\(k = 1.0999066\)
\(k\approx1.1\)
Therefore, the value of k is 1.1.
Learn more about the coefficient of variation here:
https://brainly.com/question/30992240.
#SPJ12
If 5 + 6i is a root of the polynomial function f(x), which of the following must also be a root of f(x)?
Answers
Answer:
5-6i
Step-by-step explanation:
The complex conjugate root theorem states that if (a+bi) is a root, then (a-bi) must also be a root and vice versa.
We know that (5+6i) is a root.
Then by the above theorem, (5-6i) must also be a root.
Hence, our solution is (5-6i).
The answer is (B).
Took the review test and passed.
The vertices of triangle ABC are
A (-3, -2), B (-5, -7), and C (-7, -6).
Reflect the triangle over the y-axis,
and then translate it 6 units up to form
triangle A"B"C".
Answers
Answer:
See steps below
Step-by-step explanation:
First you need you know that your pre-imagine is in the quadrant III because both x-axis and y-axis is negative and when you reflect them, the prime number would be in quadrant IV which is negative y and positive x so:
A' (3, -2)
B' (5, -7)
C'( 7, -6)
After you translate 6 unit up means y+6 so double prime will be in quadrant I and quadrant IV.
A''(3, 4)
B''(5, -1)
C''(7, 0)
\((4^{-3} )^{-2}\)
Answers
Answer:
\(4^{6}\) = 4096
Step-by-step explanation:
The rule is \((a^{b})^c\) = \(a^{bc}\).
So you can just multiply the exponents together.
-3* -2 = 6
So the answer is \(4^{6}\) which is 4096. I don't know how your professor wants you to write the answer.
A property agent sells a house for $320 000, of which he receives a commission of 1.5 %.
Calculate the amount of commission the agent receives.
Answers
Given the figure below, find the values of x and z.

Answers
Answer:
x=9 z=108
Step-by-step explanation:
72+9=81
81/9=9
x=9
72+72=144
360-144=216
216/2=108
z=108
Convert the polar equation to rectangular coordinates. (use variables x and y as needed. )
Answers
The rectangular coordinates will be (x=7cot(θ), y=7).
What are polar coordinates?A pair of coordinates locating the position of a point in a plane, the first being the length of the straight line ( r ) connecting the point to the origin, and the second the angle ( θ ) made by this line with a fixed line.
We have the standard conversion toolbox:
\(x=rcos(\theta)\\\\y=rsin(\theta)\)
Here it is given that
\(r=7cosec(\theta)\)
so
\(x=7cosec(\theta)\times cos(\theta)=\dfrac{7cos(\theta)}{sin(\theta )}=7cot(\theta)\\\\\\y=7cosec(\theta)\times sin(\theta)=\dfrac{7sin(\theta)}{sin(\theta)} = 7\)
therefore the rectangular coordinates are (7cot(θ), 7)
To know more about polar coordinates follow
https://brainly.com/question/14965899
#SPJ4
I WILL GIVE BRAINLEST
Angela has 5 fewer quarters than twice the number of her dimes. If d represents
the number of dimes Angela has, which expression represents the total number of
Angela’s quarters and dimes
PLSSS SHOW YOUR WORK PLSSSSSS
Answers
Answer:
2d-5=Q ?
Step-by-step explanation:
Am I supposed to be representing quarters too? I think this should solve it though. Lmk if somethings wrong :)
regression analysis involving one dependent variable and more than one independent variable is known as
Answers
Multiple Regression is the regression analysis involving one dependent variable and more than one independent variable.
A regression is a technique that relates a dependent variable [response] to one or more independent (explanatory) variables.
The linear regression equation is in the form, y = mx + b ., where X is an Independent variable and Y is a Dependent variable.
Multiple regression is a technique that can be used to analyze the relationship between a single dependent variable and several independent variables.
The objective of multiple regression analysis is to use the independent variables whose values are known to predict the value of the single dependent value.
Y = a + b₁X₁+ b₂X₂ + .........+ bₙXₙ
Hence, Multiple Regression analysis involving one dependent variable and more than one independent variable.
To know more about Regression analysis refer -
https://brainly.com/question/25987747
#SPJ4
anyone can help me ?
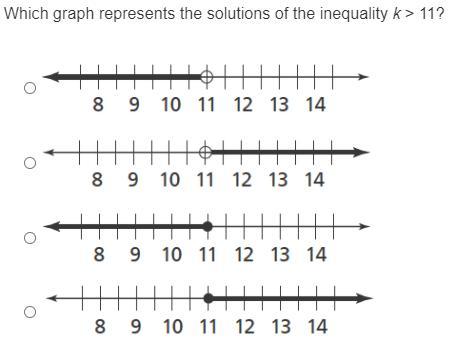
Answers
Answer:
the 4th one
Step-by-step explanation:
it shows that k is greater than 11
Peyton completed her quiz and received a score of 80%. The quiz was out of a total of 40 questions, how many questions did she get correct?
Answers
a box contains 90 balls numbered from 1 to 90. if 8 balls are drawn with replacement, what is the probability that at least two of them have the same number?
Answers
The probability that at least two of the balls have the same number is 27.40%
What is probability?Probability is the function that measures the chances that an outcome of a random event will be as expected. In this way you can measure how likely it is that an event will happen.
Probability requested is equivalent to:
P(at least 2 have same number) = 1 - P(no 2 have the same number)
P(no 2 have same number) = No. of ways to succeed / No. of possible outcomes
No. of ways to succeed = 90P8
No. of possible outcomes = 90^8
No. of ways to succeed =
nPr = n! / (n-r)!
90P8 = 90! / (90-8)!
90P8 = 90! / (82)!
90P8 = 90*89*88*87*86*85*84*83*82! / [(82)!
90P8 = 90*89*88*87*86*85*84*83
90P8 = 3.13x10^15
P(no 2 have same number) = 3.13x10^15 / 90^8
P(no 2 have same number) = 0.73
P(at least 2 have same number) = 1 - P(no 2 have the same number)
P(at least 2 have same number) = 1 - 0.73
P(at least 2 have same number) = 0.2740 = 27.40%
Learn more about probability at: brainly.com/question/251701
#SPJ4
) What is the probability that a randomly chosen miniature Tootsie Roll will weigh more than 3.50 grams
Answers
The probability that a randomly chosen miniature Tootsie Roll will weigh more than 3.50 grams is 0.1587 or 16%.
The probability of a randomly chosen miniature Tootsie Roll weighing more than 3.50 grams can be determined through statistical analysis.
To do this, we need to consider the mean and standard deviation of the weight of Tootsie Rolls.
Assuming that the weight of Tootsie Rolls follows a normal distribution, we can use the z-score formula to find the probability of a randomly chosen Tootsie Roll weighing more than 3.50 grams.
The formula for calculating the z-score is:
z = (x - μ) / σ
where x is the observed weight, μ is the mean weight, and σ is the standard deviation.
Let's assume that the mean weight of miniature Tootsie Rolls is 3 grams and the standard deviation is 0.5 grams.
To find the z-score for a weight of 3.5 grams, we can plug in the values:
z = (3.5 - 3) / 0.5
z = 1
Using a z-score table, we can find that the probability of a z-score of 1 (or a Tootsie Roll weighing more than 3.5 grams) is 0.1587.
Therefore, the probability of a randomly chosen miniature Tootsie Roll weighing more than 3.50 grams is 0.1587 or approximately 16%.
It is important to note that this is an estimate based on assumptions about the distribution of Tootsie Roll weights. The actual probability may differ depending on factors such as batch variability, production methods, and storage conditions.
know more about probability here:
https://brainly.com/question/24756209
#SPJ11
Solve for m 5m+35=70
Answers
Answer:
m=7
Step-by-step explanation:
subract 35 from both sides to isolate the variable. Then you should be left with 5m=35. From there, divide both sides to isolate the variable even more, and you should be left with m=35/5 which is 7.
Answer: m=7
Step-by-step explanation:
\(5m+35=70\)
subtract 35 on both sides
\(5m+35-35=70-35\)
\(5m=35\)
divide 5 on both sides
\(35/5=7\)
\(m=7\)
Can somebody help ??

Answers
Step-by-step explanation:
the correct answer is 1/7
1/10( x + 130) = -2(3-X)
I need help
Answers
Answer:
x = 10
Step-by-step explanation:
1/10(x + 130) = -2(3 - x)
x + 130 = -20(3-x)
x + 130 = -60 + 20x
x - 20x = -60 - 130
-19x = -190
x = 10
the employees of a company were surveyed on questions regarding their educational background and marital status. of the 600 employees, 400 had college degrees, 100 were single, and 60 were single college graduates. the probability that an employee of the company is single or has a college degree is:
Answers
The probability that an employee of the company is single or has a college degree is 7/5 or 1.4.
The probability that an employee of the company is single or has a college degree can be calculated using the principle of inclusion-exclusion.
From the given information, we know that there are 600 employees in total, 400 of whom have college degrees and 100 of whom are single. We are also given that 60 employees are both single and college graduates.
To find the probability that an employee is single or has a college degree, we can add the probabilities of being single and having a college degree and then subtract the probability of being both single and a college graduate, since we would be counting those employees twice.
Let's denote the event of an employee being single as S, and the event of an employee having a college degree as C. Using these notations, we can calculate the probability as follows:
P(S or C) = P(S) + P(C) - P(S and C)
P(S or C) = 100/600 + 400/600 - 60/600
P(S or C) = 1/6 + 2/3 - 1/10
P(S or C) = 5/10 + 10/10 - 1/10
P(S or C) = 14/10
P(S or C) = 7/5
Therefore, the probability that an employee of the company is single or has a college degree is 7/5 or 1.4.
In other words, there is a 1.4 probability that a randomly selected employee is either single or has a college degree.
To understand the calculation, we can break it down into individual probabilities. Out of the 600 employees, 100 are single, which gives us a probability of 100/600 or 1/6. Additionally, out of the 600 employees, 400 have college degrees, so the probability of having a college degree is 400/600 or 2/3.
However, if we simply add these probabilities, we would be counting the employees who are both single and college graduates twice. To correct this, we need to subtract the probability of being both single and a college graduate. From the given information, we know that there are 60 employees who fall into this category, which gives us a probability of 60/600 or 1/10.
By applying the principle of inclusion-exclusion, we add the probabilities of being single and having a college degree, and then subtract the probability of being both single and a college graduate to obtain the final probability of 7/5 or 1.4.
Learn more about principle of inclusion-exclusion here:
brainly.com/question/32375490
#SPJ11
Topic: Determining if given values are solutions to a two variable equation

Answers
Answer:
2. a & c
3. a, b & c
Step-by-step explanation:
Substitute each solutions to the question to see if you get the answer
a. 5(2)-0=10 -- so (2,0) is the solution
b. 5(3)-0=15 -- (3,0) is not the solution
c. 5(0)-(-10)=10 -- (0,-10) is the solution
d. 5(1)-(1)=4 -- (1,1) is not the solution
a. -(-4)+ 6(1) = 10 -- so (-4,1) is the solution
b. -(-22)+ 6(-2) = 10 -- so (-22,-2) is the solution
c. -(2)+ 6(2) = 10 -- so (2,2) is the solution
d. -(10)+ 6(0) = - 10 -- so (10,0) is not the solution
Which types of triangles can always be used as a counterexample to the statement "all angles in a triangle are acute"? Select all that apply.
obtuse
scalene
right
isosceles
acute
equilateral
Answers
The types of triangles which can be used as a counterexample to the statement " all angles in a triangle are acute " are:
Obtuse
Right
How to find the counter example?Counter example in math's is defined as an attempt at showing that a mathematical statement is false.
Now, in this case we want to find the counter example that all angles in a triangle are acute angles.
Now, an acute angle is defined as an angle that is less than 90 degrees.
Now, A right angle fits the counter example statement because at least one angle is not less than 90 degrees.
Similarly, an Isosceles triangle does not fit the counter example argument because in an isosceles triangle, two angles are equal and it is possible for three of the angles to be less than 90 degrees.
An obtuse triangle means that one of the angles are greater than 90 degrees and as such this fits our counter example.
Read more about Counter Example at; https://brainly.com/question/3637836
#SPJ1
wich of the following numbers are greater than -185/100 -1.08190/100-35/20
Answers
-185/100 = -1.85
a) -1.08 this number id greater than -1.85
b) 190/100 = 1.9 this number is greater than -1.85
c) -35/20 = -1.75 this number is greater than -1.85
All these numbers are greater than -185/100
How is mathematical thinking established? How can we have mathematical thinking?
修改翻译结果
Answers
Translate How is mathematical thinking established? How can we have mathematical thinking? in to Chinese.
数学思维是如何建立的? 怎样才能有数学思维?
what makes 3+7+2= +2true?
Answers
The equation 3+7+2=+2 is actually not true, but false.
Is the 3+7+2= +2true?The equation 3+7+2=+2 is actually not true, but false. This is because the sum of 3, 7, and 2 is 12, not 2.
In general, an equation is considered true if the expressions on both sides of the equal sign are equivalent in value. In this case, the expressions on the left-hand side (3+7+2) and the right-hand side (+2) are not equivalent, and therefore the equation is false.
Learn more about equation at https://brainly.com/question/14107099
#SPJ1
yo who here likes kpop give me some recs . current groups i stan are shinee , txt , stray kids , bts , and enhypen
Answers
Answer:
ITZY, BLACKPINK, TWICE, NCT, MAMAMOO, EXO, MONSTA X, LOONA, Dreamcatcher, MCND, GOT7, Red velvet, (G)I-DLE, ATEEZ, OH MY GIRL, APRIL, IZ*ONE, Super Junior, Pentagon, ASTRO, X1, EVERGLOW, IKON, WINNER, Treasure, SNSD, APINK, GFRIEND, BIG BANG, BTOB, F(x), The Rose, CNBLUE, and i have many more. :) ❤
∂²p/∂r² + 1/r ∂p/∂r = ϕμC/k ∂p/∂t
derivation of equations
1-partial derivative diffusivity equation spherical flow
2- partial derivative diffusivity equation hemi- spherical flow
Answers
The partial derivative diffusivity equation for spherical flow is ∂²p/∂r² + (1/r) ∂p/∂r = ϕμC/k ∂p/∂t, and for hemispherical flow, it is the same equation.
1. The partial derivative diffusivity equation for spherical flow is derived from the spherical coordinate system and applies to radial flow in a spherical geometry. It can be expressed as ∂²p/∂r² + (1/r) ∂p/∂r = ϕμC/k ∂p/∂t.
2. The partial derivative diffusivity equation for hemispherical flow is derived from the hemispherical coordinate system and applies to radial flow in a hemispherical geometry. It can be expressed as ∂²p/∂r² + (1/r) ∂p/∂r = ϕμC/k ∂p/∂t.
1. For the derivation of the partial derivative diffusivity equation for spherical flow, we consider a spherical coordinate system with the radial direction (r), the azimuthal angle (θ), and the polar angle (φ). By assuming steady-state flow and neglecting the other coordinate directions, we focus on radial flow. Applying the Laplace operator (∇²) in spherical coordinates, we obtain ∇²p = (1/r²) (∂/∂r) (r² ∂p/∂r). Simplifying this expression, we arrive at ∂²p/∂r² + (1/r) ∂p/∂r.
2. Similarly, for the derivation of the partial derivative diffusivity equation for hemispherical flow, we consider a hemispherical coordinate system with the radial direction (r), the azimuthal angle (θ), and the elevation angle (ε). Again, assuming steady-state flow and neglecting the other coordinate directions, we focus on radial flow. Applying the Laplace operator (∇²) in hemispherical coordinates, we obtain ∇²p = (1/r²) (∂/∂r) (r² ∂p/∂r). Simplifying this expression, we arrive at ∂²p/∂r² + (1/r) ∂p/∂r.
In both cases, the term ϕμC/k ∂p/∂t represents the source or sink term, where ϕ is the porosity, μ is the fluid viscosity, C is the compressibility, k is the permeability, and ∂p/∂t is the change in pressure over time.
These equations are commonly used in fluid mechanics and petroleum engineering to describe radial flow behavior in spherical and hemispherical geometries, respectively.
To learn more about partial derivative, click here: brainly.com/question/2293382
#SPJ11
if a student is chosen at random, what is the probability that the student prefers the zoo or the water park?
Answers
Without specific data on the number of students who prefer each option, we cannot calculate the probability.
To determine the probability that a student prefers the zoo or the water park, we need to know the total number of students and the number of students who prefer each option. Without this information, it is not possible to calculate the probability accurately.
To calculate the probability, we would need to divide the number of students who prefer the zoo or the water park by the total number of students. For example, if there are 50 students in total and 30 prefer the zoo and 20 prefer the water park, the probability would be:
P(prefer zoo or water park) = (30 + 20) / 50 = 50 / 50 = 1
However, without specific data on the number of students who prefer each option, we cannot calculate the probability.
For more questions on probability
https://brainly.com/question/251701
#SPJ8
Problem 2 (21 points) The random variables X and Y have joint pdf fX,Y(x,y)=2e−x−y,0
Answers
1. P(X + Y ≤ 2) = -e⁻² - 2e⁻², 2. Marginal PDF for X: fₓ(x) = -2e⁻ˣ and marginal PDF for Y: fᵧ(y) = 2e⁻ʸ - 2e⁻ˣ⁻ʸ.
1. To find P(X + Y ≤ 2), we need to integrate the joint PDF over the region where X + Y is less than or equal to 2. Since X and Y are non-negative random variables, the region of interest is the triangle bounded by the lines X = 0, Y = 0, and X + Y = 2. Integrating the joint PDF over this region gives:
P(X + Y ≤ 2) = ∫∫ fₓᵧ(x, y) dx dy
The integral bounds can be determined by considering the constraints 0 ≤ X ≤ Y ≤ ∞:
0 ≤ x ≤ y
0 ≤ y ≤ ∞
Setting up the integral,
P(X + Y ≤ 2) = ∫[0,∞] ∫[x,2-x] 2e⁻ˣ⁻ʸ dy dx
Solving the integral,
P(X + Y ≤ 2) = ∫[0,∞] -2e⁻ˣ⁻ʸ ∣ x to 2-x dx
Simplifying the integral bounds,
P(X + Y ≤ 2) = ∫[0,∞] -2e⁻ˣ⁻²⁻ˣ + 2e⁻²⁻ˣ dx
Evaluating the integral,
P(X + Y ≤ 2) = -e⁻²⁻ˣ - 2e⁻²⁻ˣ ∣ 0 to ∞
As x approaches infinity, e⁻²⁻ˣ approaches 0, so the second term in the integral becomes zero.
P(X + Y ≤ 2) = -e⁻²⁻⁰ - 2e⁻²⁻⁰
P(X + Y ≤ 2) = -e⁻² - 2e⁻²
Therefore, P(X + Y ≤ 2) = -e⁻² - 2e⁻².
2. To find the marginal PDFs for X and Y, we integrate the joint PDF over the respective variable while treating the other variable as a constant. The marginal PDF for X, denoted as fₓ(x), is obtained by integrating the joint PDF fₓᵧ(x, y) over the range of Y:
fₓ(x) = ∫[x,∞] fₓᵧ(x, y) dy
Substituting the given joint PDF,
fₓ(x) = ∫[x,∞] 2e⁻ˣ⁻ʸ dy
Simplifying the integral,
fₓ(x) = -2e⁻ˣ⁻ʸ ∣ x to ∞
As y approaches infinity, e⁻ˣ⁻ʸ approaches 0, so the integral becomes,
fₓ(x) = -2e⁻ˣ⁻ˣ
Simplifying further,
fₓ(x) = -2e⁻ˣ
Therefore, the marginal PDF for X is fₓ(x) = -2e⁻ˣ.
Similarly, the marginal PDF for Y, denoted as fᵧ(y), is obtained by integrating the joint PDF fₓᵧ(x, y) over the range of X,
fᵧ(y) = ∫[0,y] fₓᵧ(x, y) dx
Substituting the given joint PDF,
fᵧ(y) = ∫[0,y] 2e⁻ˣ⁻ʸ dx
Simplifying the integral,
fᵧ(y) = 2e⁻ˣ⁻ʸ ∣ 0 to y
fᵧ(y) = 2e⁻ʸ - 2e⁻ˣ⁻ʸ
Therefore, the marginal PDF for Y is fᵧ(y) = 2e⁻ʸ - 2e⁻ˣ⁻ʸ.
To know more about Probability density function (PDF), visit,
https://brainly.com/question/30403935
#SPJ4
Complete question - Let the random variables X and Y have the joint PDF given below:
fₓᵧ(x, y) = 2e⁻ˣ⁻ʸ when 0 ≤ X ≤ Y ≤ ∞
fₓᵧ(x, y) = 0 otherwise.
1. Find P(X + Y ≤ 2)
2. Find the marginal PDF for X and Y.
What is the diffrent between statistical significance and practical significance
Answers
The concept of statistical significance is mathematically defined and widely accepted by those who use it to assess the usefulness of scientific claims.
However, there is no single definition for practical significance. It is subjective in nature, experiential, and each person decides what it is based on their own experiences.
Thus, it is clear that while Practical significance lacks a common definition, statistical significance has a mathematical definition and is widely accepted by those who use it to assess the usefulness of scientific claims. It is a subjective concept that each person decides for themselves based on their personal experiences.
To learn more about statistical significance visit link :
brainly.com/question/8362659
#SPJ4
solve this equation
4f+2=6f-12
Answers
Let's try to understand how we can solve this equation
Given equation,4f+2=6f-12
Now we will take the terms on one side and constants on the other.
=> 2+12=6f-4f
=> 14=2f
=>7=f
So, the value of f would be 7. Remember that while bringing value to another side, the sign of that value changes. If it is a positive sign then it is going to be transformed into a negative one and vice versa.
Question
Ms. Ellis expected 50 families to attend parent–teacher conferences, but 60 families attended. What is the percent error?
Answers
Answer: 20%
Step-by-step explanation:
The expected value was 50, the value in reality was 60, so
(60 - 50) / 50
= 10/50
= 1/5
To convert to a percent we multiply by 100:
= 20%.