How do you solve: 4/5 ÷ 10
Answers
Answer:
8
Step-by-step explanation:
4/5 ÷ 10
4/5 ÷ 10/1 Multiply the denominators and numerators
= 40/5 then Simplify
8
Related Questions
37.
An express train travelled at a certain average speed from Town X to Town Y which was
150 km away. It then continued its journey to Town Z at an average speed 20 km/h faster than
its initial average speed. Town Ywas 200 km from Town Z. If it took the same time to travel for
both parts of the journey, what was the train's average speed for the first part of the journey?
Answers
Answer:
60 km/hr
Step-by-step explanation:
Let the speed at the initial average speed from Town X to Town Y be a.
We are told that it journeyed to Town Z at an average speed 20 km/h faster than its initial average speed. Thus, its average speed here is (a + 20) km/hr.
Town Y was 200 km from Town Z.
Thus, time spent here is;
t_2 = 200/(a + 20)
Time from X to Y is; t_1 = 150/a
We are told that it took the same time to travel for both parts of the journey.
Thus; t_1 = t_2
150/a = 200/(a + 20)
Cross multiply to get;
150(a + 20) = 200a
150a + 3000 = 200a
200a - 150a = 3000
50a = 3000
a = 3000/50
a = 60 km/hr
Find the nature of the roots of 4x ^ 2 + 6x - 7 = 0
a. complex
b. irrational
c. rational
d. real and equal
Answers
Answer:
b
Step-by-step explanation:
given a quadratic equation in standard form
ax² + bx + c = 0 (a ≠ 0 )
the discriminant b² - 4ac informs us about the nature of the roots
• If b² - 4ac > 0 then roots are real and irrational
• If b² - 4ac > 0 abd a perfect square then roots are real and rational
• If b² - 4ac = 0 then roots are real and equal
• If b² - 4ac < 0 the roots are complex
4x² + 6x - 7 = 0 ← is in standard form
with a = 4, b = 6, c = - 7 , then
b² - 4ac = 6² - (4 × 4 × - 7) = 36 - (- 112) = 36 + 112 = 148
since b² - 4ac > 0 then roots are real and irrational
Write a function rule for the given situation. Do not use spaces in your answers and use x and y as your variables.
(help me out pls )
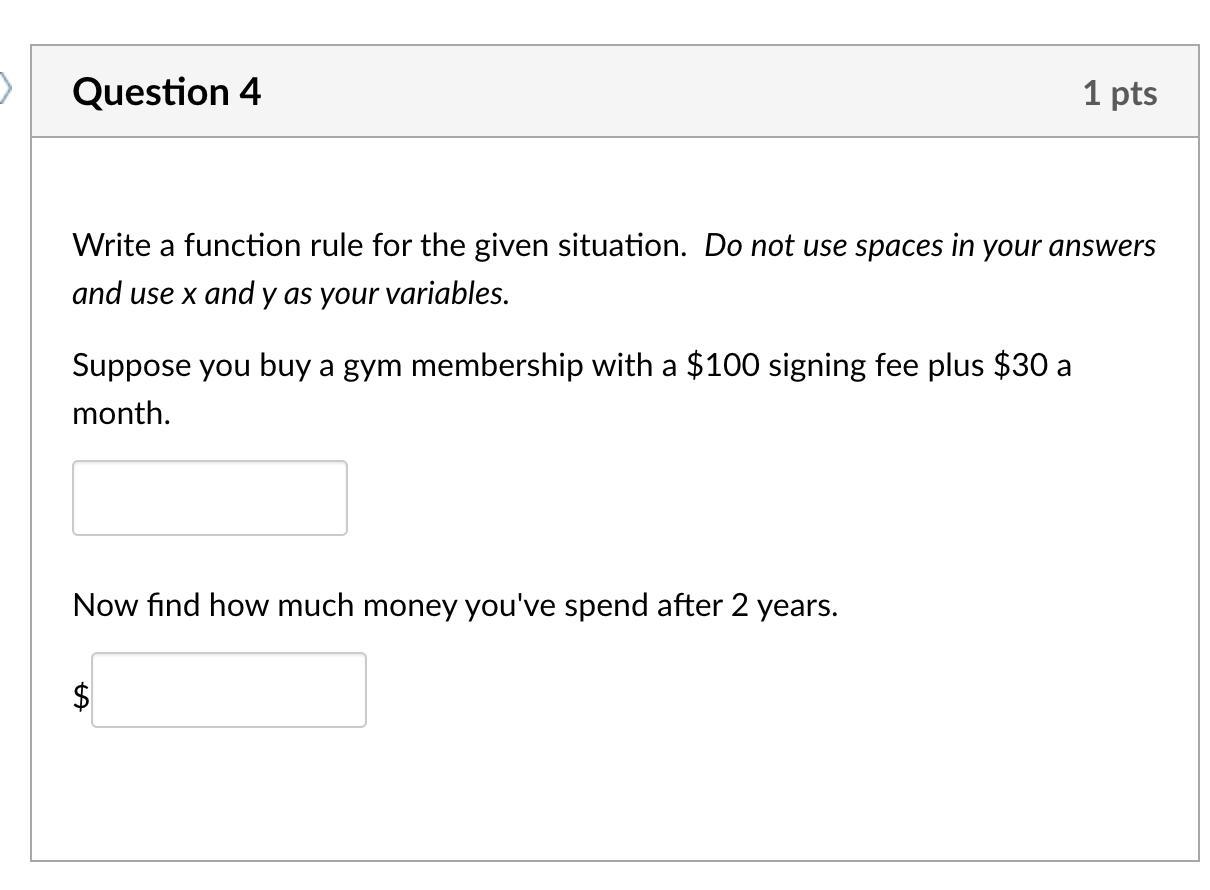
Answers
The situation can be modeled with the linear function:
f(x) = $30*x + $100
Evaluating that, we can see that after two years you will pay $820.
How to write a function rule for the situation?Here we know that you buy a gym membership for $100 plus $30 per month.
So, the cost after x months can be modeled by the linear function:
f(x) = $30*x + $100
Where x is the number of months and f(x) is the amount of money that you pay after x months.
We want to find how much you will pay after 2 years, there are 24 months in two years, then we will get:
f(24) = $30*24 + $100 = $820
Learn more about linear functions:
https://brainly.com/question/4025726
#SPJ1
A car drove 10/45 miles in 0.4 hours. How fast was the car traveling in miles per hour?
Answers
Answer:
1.2 hours equal to 30mph
Step-by-step explanation:
Pls mark brainliest
Name the property of addition modeled here.
If a = b, then a + c = b + c.
A. Addition Property of Equality
B. Commutative Property of Addition
C. Associative Property of Addition
D. None of the above
Answers
Answer:
Addition Property of Equality, or A
Step-by-step explanation:
This is the definition of addition property of equality
Solve the initial value problemf’(x) = 1/x - 2x + x^1/2; f(4) = 2

Answers
SOLUTION:
Case: Initial value problem
An initial value problem is an ordinary differential equation together with an initial condition that specifies the value of the unknown function at a given point in the domain
To solve the initial value problem, we have a value of the derivative of y when x is known.
y'(x)= value
Given:
f(4)=2
\(\begin{gathered} f^{\prime}(x)=\frac{1}{x}-2x+x^{\frac{1}{2}} \\ Integrating \\ f(x)=ln(x)-\frac{2x^2}{2}+\frac{2x^{\frac{3}{2}}}{3}+C \\ f(x)=ln(x)-x^2+\frac{2x^{\frac{3}{2}}}{3}+C \\ f(4)=2 \\ f(4)=ln(4)-2(4)^2+\frac{2(2)^{\frac{3}{2}}}{3}+C \\ 2=1.386-32+1.8856+C \\ C=2-1.3863+32-1.8856 \\ C=30.7281 \end{gathered}\)The resulting equation will be:
\(f(x)=\ln x-x^2+\frac{2x^{\frac{3}{2}}}{3}+30.7281\)Final answer:
\(f(x)=\operatorname{\ln}x-x^2+\frac{2x^{\frac{3}{2}}}{3}+30.7281\)Ron bought a cycle for $800 and sold it at a loss of $160. What is his selling price?
Answers
Answer:
640
Step-by-step explanation:
800-160=640...............................
Answer:
$800-$160
=$640
Hope it helps.
3) [14pts] Find the horizontal and vertical asymptotes of the graph of the function f(x)=x+3) [14pts] Find the horizontal and vertical asymptotes of the graph of the function f(x)=x+x2+∣x∣+ln∣x∣1.2+∣x∣+ln∣x∣1.
Answers
For the function f(x) = x + 3, there is a horizontal asymptote at y = 3 and no vertical asymptotes. For the function f(x) = x + x^2 + |x| + ln(|x|^(1/2) + |x| + ln(|x|^(1/2), there are no horizontal asymptotes and no vertical asymptotes.
For the function f(x) = x + 3, as x approaches positive or negative infinity, the value of f(x) approaches infinity. Therefore, there is no horizontal asymptote. Additionally, since the function does not contain any terms that cause division by zero or undefined behavior, there are no vertical asymptotes.
For the function f(x) = x + x^2 + |x| + ln(|x|^(1/2) + |x| + ln(|x|^(1/2), we need to analyze the behavior as x approaches positive or negative infinity.
As x approaches positive or negative infinity, the dominant term in the function is x^2. Therefore, as x goes to positive or negative infinity, the value of f(x) approaches infinity. This means there is no horizontal asymptote.
Regarding vertical asymptotes, we need to check if there are any values of x for which the function is undefined. In this case, the function is defined for all real numbers except x = 0, where the term ln(|x|^(1/2) is not defined. Therefore, there is no vertical asymptote.
In conclusion, the function f(x) = x + 3 has a horizontal asymptote at y = 3 and no vertical asymptotes. The function f(x) = x + x^2 + |x| + ln(|x|^(1/2) + |x| + ln(|x|^(1/2) has no horizontal asymptotes and no vertical asymptotes.
Learn more about function here:
brainly.com/question/30721594
#SPJ11
Solve for x. Figures are not necessarily drawn to scale.

Answers
Check the picture below.
\(\cfrac{17.5+14}{17.5}~~ = ~~\cfrac{x}{12.5}\implies \cfrac{(17.5+14)(12.5)}{17.5}~~ = ~~x\implies 22.5=x\)

Suppose that you want to design an experiment to study the proportion of unpopped kernels of popcorn.
(i)State and explain the pre-experimental planning for this experiment designs
(ii) State two major sources of variation that would be difficult to control in this experiment.
Answers
(i) The pre-experimental planning is clear research, précised sample size, sampling method, experimental design and protocol. (ii) Two major sources of variation that would be difficult to control are Environmental factors and Variation in the quality.
(i) The pre-experimental planning for this experiment design would include the following steps:
Clearly define the research question and the population of interest.
Determine the sample size required to achieve a desired level of precision and confidence.
Identify the appropriate sampling method to use (e.g., simple random sampling, stratified sampling, cluster sampling).
Determine the appropriate experimental design to use (e.g., randomized controlled trial, quasi-experimental design).
Develop a detailed experimental protocol, including the procedures for collecting and recording data, as well as any necessary ethical considerations.
(ii) Two major sources of variation that would be difficult to control in this experiment are:
Environmental factors, such as temperature, humidity, and atmospheric pressure, which can affect the popping rate of popcorn kernels.
Variation in the quality of the popcorn kernels themselves, such as differences in moisture content, size, and shape, which can affect the popping rate.
Know more about Variation here:
https://brainly.com/question/31108545
#SPJ11
is -6 greater than 3
Answers
Answer: no 3 is grade then -6 as 3 is positive number and 6 is negative number so positive is greater then negative number.
Step-by-step explanation:
In order to indicate if a number is greater than or less than another, we use the symbols > and <. For example, 10 is greater than 3, so we write it 10 > 3.
a survey of 130 college graduates was conducted. students were asked whether they were employed and if they were looking for a job. the following table shows the results. job searching no job searching total employed 28 61 89 not employed 18 23 41 total 46 84 130 according to the table, what is the probability that a randomly chosen student is not employed given that they are job searching? give your answer as a fraction in simplest form.
Answers
The probability that a randomly chosen student is not employed given that they are job searching is 9/23.
What is the probability that a randomly chosen person is not employed despite job searching
The probability of a student not being employed given that they are job searching is given by the conditional probability:
P(not employed | job searching) = P(not employed and job searching) / P(job searching)
We can find the probabilities for the numerator and denominator from the table:
P(not employed and job searching) = 18
P(job searching) = 46
Therefore, the conditional probability is:
P(not employed | job searching) = 18 / 46
We can simplify this fraction by dividing both the numerator and denominator by their greatest common factor, which is 2:
P(not employed | job searching) = 9 / 23
Learn more probability here;
https://brainly.com/question/23286309
#SPJ1
How many cents are in n nickels and c cents?
Answers
Using proportions, it is found that there are c + 0.25n cents in n nickels and c cents.
What is a proportion?A proportion is a fraction of a total amount. To solve problems involving proportions, such as this one, multiplications of the amounts and their values are made.
In this problem, we consider that each nickel has 0.25 cents, hence, there are c + 0.25n cents in n nickels and c cents.
More can be learned about proportions at https://brainly.com/question/24372153
#SPJ1
c+0.25n cents is the answer.
Solve for x. Thank you

Answers
Answer:
20
Step-by-step explanation:
Let the angle at the left corner is A, so the angle at the rIght corner should be (180-90-A) = (90-A).
In the left triangle:
tanA = 8√5/16 = √(5)/2
Thus,
cotA = 1/tanA = 2/√5
In the right triangle:
tan(90-A) = 8√5/x
cotA = 8√5/x [tan(90-x) = cotx]
2/√5 = 8√5/x
x = 20
Find the value of x
Thank you!

Answers
24/x = 3
X=24/3 = 8
Answer:X is 8
Step-by-step explanation:
24º and 36º,what is 24 of 36? It is 2/3.
Then what is 2/3 of 12?It is 8 .
So X is 8.
Hope this helped!
Good luck !
Tell me if it’s wrong!
lfu29
Differentiation
Please help me!

Answers
Answer:
\( \frac{dy}{dx} = - 1 \frac{5}{9} \)
Step-by-step explanation:
Please see the attached picture for the full solution.
☆ \(\frac{1}{x} = x^{ - 1} \)

Please help me.
2 ^ (2x - 3) * .5 ^ (x - 1) = 200
Answers
Answer:
x = 3
Step-by-step explanation:
\( {2}^{(2x - 3)} \ast {5}^{(x - 1)} = 200 \\ \\ \implies \: {2}^{(2x - 3)} \ast {5}^{(x - 1)} =8 \ast \: 25 \\ \\\implies \: {2}^{(2x - 3)} \ast {5}^{(x - 1)} = {2}^{3} \ast {5}^{2} \)
Comparing like terms on both sides, we find:
\({2}^{(2x - 3)}= {2}^{3}\: \: or \:\:{5}^{(x - 1)} = {5}^{2} \)
\(\implies \:2x - 3 = 3 \: \: or \: \:x - 1 = 2 \\ \\ \implies \:2x = 3 + 3 \: \: or \: \: x = 1 + 2\\ \\ \implies \:2x = 6 \: \: or \: \: x = 3 \\ \\ \implies \:x = \frac{6}{3} \: \: or \: \: x = 3 \\ \\ \implies \:x = 3 \: \: or \: \: x = 3 \\ \\ \implies \huge \:x = 3 \)
If we invest $100,000 today in an account earning 7% per year,
how many years until we have $500,000? Round to two decimals.
Answers
It would take approximately 19.65 years for an investment of $100,000 at a 7% annual interest rate to grow to $500,000. Rounded to two decimal places, the answer is 19.65 years.
To determine the number of years it will take for an investment of $100,000 at a 7% annual interest rate to grow to $500,000, we can use the compound interest formula:
A = P(1 + r/n)^(nt)
Where:
A = the future value of the investment ($500,000)
P = the initial principal amount ($100,000)
r = the annual interest rate (7% or 0.07)
n = the number of times that interest is compounded per year (assuming annually, so n = 1)
t = the number of years
Plugging in the values we know, we get:
$500,000 = $100,000(1 + 0.07/1)^(1*t)
Dividing both sides of the equation by $100,000 and simplifying:
5 = (1.07)^t
To solve for t, we can take the logarithm of both sides:
log(5) = log[(1.07)^t]
Using logarithmic properties, we can bring down the exponent:
log(5) = t * log(1.07)
Finally, we can solve for t by dividing both sides by log(1.07):
t = log(5) / log(1.07)
Using a calculator, we find:
t ≈ 19.65
Therefore, it would take approximately 19.65 years for an investment of $100,000 at a 7% annual interest rate to grow to $500,000. Rounded to two decimal places, the answer is 19.65 years.
Learn more about investment from
https://brainly.com/question/24703884
#SPJ11
A 3 foot-wide wood deck will be built around a rectangular-shaped pool that measures 15 feet by 30 feet. The resulting shape is also rectangular. If the lumber cost $10 per square yard, what is the cost of the wood for the deck?
Answers
The answer is $1500.00
\(\begin{gathered} \text{Area of the rectangular shped pool=L}\times B \\ \text{Area}=30\times15=450ft^2 \\ \text{Note: 3 f}eet=1\text{ yard} \\ So,\text{ }\frac{450}{3}=150persquare\text{ yards} \\ 150\text{ Yards =10}\times150=\text{ \$1500.00} \end{gathered}\)Suppose that 20% of voters are in favor of certain legislation- A large number n of voters are polled and a relative frequency estimate £3111} for the above proportion is obtained. a) Use the Chebyshev inequality to determine 1101? many voters should be polled in order that the probability is at least 0.95 that fan) differs from 0.20 by less than 0.02. b} Use central limit theorem to determine how many voters should be polled in order that the probability is at least 0.95 that £311: 11} differs from 0.20 by less than 0.02.
Answers
A. To ensure that the probability is at least 0.95 that the relative frequency estimate differs from 0.20 by less than 0.02, at least 7976 voters should be polled.
b. We find the z-score corresponding to a cumulative probability of 0.95 to be approximately 1.96.
n > 2401
a) Using the Chebyshev inequality, we can determine the minimum number of voters that should be polled to ensure that the probability is at least 0.95 that the relative frequency estimate differs from 0.20 by less than 0.02.
The Chebyshev inequality states that for any random variable X with mean μ and standard deviation σ, the probability of X deviating from the mean by k standard deviations is at least 1 - 1/k^2.
In this case, we want the relative frequency estimate to deviate from 0.20 by less than 0.02, which means we want the difference to be within 0.02 standard deviations of the mean. Since the relative frequency estimate is a sample proportion, its standard deviation can be approximated by sqrt(p(1-p)/n), where p is the true proportion (0.20) and n is the sample size.
We can set up the inequality as follows:
1 - 1/k^2 ≥ 0.95
Solving for k:
1/k^2 ≤ 0.05
k^2 ≥ 1/0.05
k^2 ≥ 20
Taking the square root of both sides:
k ≥ sqrt(20)
k ≥ 4.47
To ensure that the difference between the relative frequency estimate and 0.20 is within 0.02, we need k standard deviations to be less than 0.02. So, we have:
k * sqrt(p(1-p)/n) < 0.02
4.47 * sqrt(0.20(1-0.20)/n) < 0.02
Simplifying:
sqrt(0.20(1-0.20)/n) < 0.02/4.47
sqrt(0.16/n) < 0.00448
0.4/sqrt(n) < 0.00448
sqrt(n) > 0.4/0.00448
sqrt(n) > 89.29
n > 89.29^2
n > 7975.84
Therefore, to ensure that the probability is at least 0.95 that the relative frequency estimate differs from 0.20 by less than 0.02, at least 7976 voters should be polled.
b) Using the central limit theorem, we can determine the minimum number of voters that should be polled to ensure that the probability is at least 0.95 that the sample mean differs from 0.20 by less than 0.02.
According to the central limit theorem, the sample mean follows a normal distribution with mean μ and standard deviation σ/sqrt(n), where σ is the population standard deviation (unknown in this case), and n is the sample size.
To ensure that the difference between the sample mean and 0.20 is within 0.02, we can set up the following inequality:
z * (σ/sqrt(n)) < 0.02
Since the population standard deviation σ is unknown, we can use a conservative estimate by assuming the worst-case scenario, which is p(1-p) = 0.25. Therefore, σ = sqrt(0.25) = 0.5.
Using the standard normal distribution table, we find the z-score corresponding to a cumulative probability of 0.95 to be approximately 1.96.
1.96 * (0.5/sqrt(n)) < 0.02
0.98/sqrt(n) < 0.02
sqrt(n) > 0.98/0.02
sqrt(n) > 49
n > 49^2
n > 2401
Learn more about probability from
https://brainly.com/question/30390037
#SPJ11
6. Find (a) the domain, (b) all the critical points, and (c) use The Second Derivative Test to classify them. g(x) = 6x + sin(3x), 0
Answers
The domain of the function g(x) = 6x + sin(3x) is all real numbers since both the linear term 6x and the sine term sin(3x) are defined for any value of x.
To find the critical points of g(x), we need to find the values of x where the derivative of g(x) is equal to zero or undefined. Taking the derivative of g(x), we have g'(x) = 6 + 3cos(3x). Setting this derivative equal to zero, we solve the equation 6 + 3cos(3x) = 0 to find the critical points.
To classify the critical points, we can use the Second Derivative Test. Taking the second derivative of g(x), we have g''(x) = -9sin(3x). Evaluating g''(x) at each critical point found in step (b), we can determine the concavity of the function at those points.
Learn more about critical points here :
https://brainly.com/question/32077588
#SPJ11
Which comparison is not correct?
8 > -9
-7 > -9
-8 < -4
-2 < -9
Answers
Answer:
-2>-9
The larger the negative numbers , the smaller it is
Helppp ...............

Answers
Answer:
i think its B
Step-by-step explanation:
im not sure but im pretty sure if its wrong im sorry but im pretty sure its correct
Why does the base matter when simplifying negative exponents?
Answers
Answer:
A negative exponent just means that the base is on the wrong side of the fraction line, so you need to flip the base to the other side. For instance, "x–2" (pronounced as "ecks to the minus two") just means "x2, but underneath, as in 1 x 2 \frac{1}{x^2} x21 ".
Step-by-step explanation:
the letters of the word `sixteen' are randomly arranged. what is the probability that the two e's are not next to each other?
Answers
The probability of getting e's not next to each other is 0.05.
What is probability?Probability is defined as the ratio of the number of favourable outcomes to the total number of outcomes in other words the probability is the number that shows the happening of the event.
Probability = Number of favourable outcomes / Number of sample
Given that the letters of the word `sixteen' are randomly arranged.
The arrangement of the e's not to come next to each other is, 3! and the total arrangement will be 5!
The probability will be calculated as,
P = (3!/5!)
P = (3x 2) / (5x4x3x2x1)
P = 1 / 20
P = 0.05
Therefore, the probability of getting e's not next to each other is 0.05.
To know more about probability follow
https://brainly.com/question/25870256
#SPJ1
jam's preferences over (x
1
,x
2
) bundles are described by the utility function, U(x
1
,x
2
)=x
1
1/2
+x
2
=
x
1
+x
2
. Which is the correct expression for Sam's MRS function?
MRS=
x
2
x
1
MRS=2
x
1
MRS=
x
1
x
2
MRS=
2
x
1
1
Answers
The correct expression for Sam's MRS function, based on Jam's utility function, is MRS = 1/2 * x₁⁻¹/₂.
The marginal rate of substitution (MRS) measures the rate at which an individual is willing to give up one good in exchange for another while keeping the utility constant. It represents the slope of the indifference curve, which shows the combinations of goods that yield the same level of utility.
Let's start by finding the partial derivatives of Jam's utility function with respect to x₁ and x₂:
∂U/∂x₁ = 1/2 * x₁⁻¹/₂ (partial derivative of x₁^(1/2) with respect to x₁)
∂U/∂x₂ = 1 (partial derivative of x₂ with respect to x₂)
Now, to calculate the MRS, we need to find the ratio of these partial derivatives:
MRS = (∂U/∂x₁) / (∂U/∂x₂)
Substituting the partial derivatives we calculated earlier, we get:
MRS = (1/2 * x₁⁻¹/₂) / 1
Simplifying further, we can rewrite it as:
MRS = 1/2 * x₁⁻¹/₂
To know more about expression here
https://brainly.com/question/14083225
#SPJ4
use the shell method to find the volume of the solid generated by revolving the region bounded by y =4x-3, y =√x, and x = 0 about the y-axis.
the volume is _____ cubic units.
Answers
The volume of the solid produced by revolving the region limited by y = 4x - 3, y = √x, and x = 0 about the y-axis is 13.122 cubic units.
To determine the volume of the solid produced by revolving the region limited by y = 4x - 3, y = √x, and x = 0 about the y-axis, use the shell method.
When using the shell approach, use vertical shells for the variable being rotated around the y-axis. The volume of the shell can be determined using the following formula:2πrhΔx, where h is the height of the shell, r is the distance between the shell's axis of rotation and the curve, and Δx is the thickness of the shell.
To calculate the volume, first locate the limits of integration, which in this case are 0 to 1. To obtain the height and radius of the shell, solve for x in terms of y.
The volume is obtained by summing the volumes of the shells. Substitute the given values in the formula, to get the required answer.
To know more about shell method click on below link:
https://brainly.com/question/30401636#
#SPJ11
QUESTION 14 How long does it take for $14050 to grow to $26500, if interest rates are set at 15%? O 4.54 years O 423.33 years O 0.59 years O 12.23 years
Answers
To calculate the time it takes for $14,050 to grow to $26,500 with an interest rate of 15%, we can use the formula for compound interest and solve for time. The correct answer is 12.23 years.
The formula for compound interest is given by the formula: A = P(1 + r/n)^(n*t), where A is the final amount, P is the principal amount, r is the interest rate, n is the number of times interest is compounded per year, and t is the time in years.
In this case, the initial amount (P) is $14,050, the final amount (A) is $26,500, and the interest rate (r) is 15%. We need to solve for time (t).
\($26,500= $ 14,050(1 + 0.15/n)^{(n*t)}\)
By substituting values into the equation and solving for t, we find:
t ≈ 12.23 years
Therefore, it will take approximately 12.23 years for $14,050 to grow to $26,500 with an interest rate of 15%.
Learn more about rates here:
https://brainly.com/question/199664
#SPJ11
h(s)=u
0
k
s
What is the name of this function? What is the argument of the function? (aka independent variable) What are the parameters of this functions?
Answers
The function h(s) = u0k(s) represents the velocity distribution in a channel or pipe flow, where k(s) is the hydraulic gradient, and u0 is the mean velocity. This function is also known as the power law velocity profile or non-Newtonian velocity profile.
h(s) represents the velocity at a particular point s, where s is the independent variable or argument of the function. The parameters of this function are u0 and k(s), which vary depending on the fluid's properties and the geometry of the channel or pipe. The function h(s) = u0k(s) represents the velocity distribution in a channel or pipe flow. This function is also known as the power law velocity profile or non-Newtonian velocity profile. Non-Newtonian fluids are those whose viscosity varies with the rate of deformation. These fluids are often encountered in many industrial processes such as polymer processing, petroleum production, food processing, and wastewater treatment.The power law velocity profile is an important model for describing the flow of these fluids. This model is based on the assumption that the fluid behaves like a power-law fluid. A power-law fluid is a fluid whose viscosity is proportional to a power law of the shear rate. The power law index, n, is a measure of the fluid's shear-thinning or shear-thickening behavior.In the power law velocity profile, the velocity at a particular point s is given by the product of the mean velocity u0 and the hydraulic gradient k(s). The hydraulic gradient is the slope of the energy line, which is a measure of the energy dissipation rate due to friction. The hydraulic gradient varies along the length of the channel or pipe, and it depends on the geometry of the flow domain and the fluid's properties.The power law velocity profile has several important properties. First, it provides a good fit to the experimental data for non-Newtonian fluids. Second, it allows for the prediction of the velocity distribution in complex geometries, which is important in many engineering applications. Finally, it provides insight into the physics of the flow, which is important for understanding the behavior of non-Newtonian fluids.
In conclusion, the function h(s) = u0k(s) represents the power law velocity profile or non-Newtonian velocity profile. The argument of the function is s, which represents the distance along the length of the channel or pipe. The parameters of the function are u0 and k(s), which vary depending on the fluid's properties and the geometry of the channel or pipe. The power law velocity profile is an important model for describing the flow of non-Newtonian fluids. This model is based on the assumption that the fluid behaves like a power-law fluid, and it provides a good fit to the experimental data for non-Newtonian fluids.
To learn more about non-Newtonian velocity profile visit:
brainly.com/question/13348313
#SPJ11
Examine the Graph.
HELP FOR POINTS

Answers
Step-by-step explanation:
I will definitely explain you if you follow me