How is 19-2 equal to 20
Answers
Answer:
It is not.
Step-by-step explanation:
19-2 is equal to 17.
This is because when subtracting, we go backwards on a number line, so if we start at 19 and go back 2 spaces, we'll land at 17.
The left side 17 does not equal to the right side 20, which means that the given statement is false.
False.
Not possible.
Related Questions
sketch the graphs using 3 points that belong to it y = -3x +2
Answers
Answer:
Step-by-step explanation:

Answer:
0,2
1,-1
2,-4
Step-by-step explanation:
If eggs cost $3 per dozen, how much would 8 eggs cost?
Answers
Answer:
$2
Step-by-step explanation:
Because 3/12 is 0.25 and then you multiply it by 8 to get 2.
A scientist has two solutions, which she has labeled Solution A and Solution B. Each contains salt. She knows that Solution A is 45% salt and Solution B is
95% salt. She wants to obtain 60 ounces of a mixture that is 85% salt. How many ounces of each solution should she use?
Answers
we know A is 45% salt, so the amount of salt in A is (45/100)*A or 0.45A.
likewise we know that B is 95% salt, so the salt amount in it is (95/100)*B or 0.95B.
\(\begin{array}{lcccl} &\stackrel{solution}{quantity}&\stackrel{\textit{\% of }}{amount}&\stackrel{\textit{oz of }}{amount}\\ \cline{2-4}&\\ A&x&0.45&0.45x\\ B&y&0.95&0.95y\\ \cline{2-4}&\\ mixture&60&0.85&51 \end{array}~\hfill \begin{cases} x+y=60\\ 0.45x+0.95y=51\\[-0.5em] \hrulefill\\ y = 60 -x \end{cases}\)
\(\stackrel{\textit{substituting on the 2nd equation}}{0.45x+0.95(60-x) = 51}\implies 0.45x+57-0.95x=51 \\\\\\ 0.45x-0.95x=-6\implies -0.5x=-6\implies x = \cfrac{-6}{-0.5} \\\\\\ \boxed{x = 12}~\hfill \stackrel{\textit{we know that}}{y = 60 -x}\implies \boxed{y=48}\)
Evaluate. 10/1·(−4) Enter your answer in the box.
I’ll give brainliest if its correct on the test! (And if i can figure out how)
Answers
Step-by-step explanation:
10/1(-4)
10(-4)
=-2.5 or 5/-2
What is the solution to |x-2| + 3 > 17?
Ox<-12 or x > 16
Ox<-14 or x>7
O-12
O-14
Answers
Answer:
x<-12 or x>16
Step-by-step explanation:
Answer:
|x - 2| + 3 > 17
|x - 2| > 14
x - 2 < -14 or x - 2 > 14
x < -12 or x > 16
5. Apply Math Models A science teacher uses a fair spinner
simulate choosing 1 of 5 different field trips for her classes.
spinner has 5 equal sections, each representing a different
trip. The teacher spins the spinner 50 times and records the
results in the table below.
Answers
Experimental and theoretical probabilities do not match; Field Trip B is the most popular with 32% relative frequency.
What is frequency?
Frequency refers to the number of times an event or observation occurs within a given period, sample size, or population. In the context of data analysis, frequency is often used to describe how often a particular value or category appears in a dataset or sample. It can be expressed as an absolute frequency (the actual number of times an event occurred) or a relative frequency (the proportion or percentage of times an event occurred compared to the total number of observations).
The experimental probability of selecting each field trip can be calculated by dividing the number of times each trip was selected by the total number of spins. For example, the experimental probability of selecting Field Trip A is 8/50 = 0.16 or 16%, the experimental probability of selecting Field Trip B is 16/50 = 0.32 or 32%, and so on.
The theoretical probability of selecting each field trip is 1/5 or 0.2 or 20%. This is because the spinner has 5 equal sections, and each section represents a different trip.
The experimental and theoretical probabilities do not match exactly. For example, the experimental of selecting Field Trip B is 0.32 or 32%, while the theoretical probability is only 0.2 or 20%. This could be due to chance or random variation, as the teacher only spun the spinner 50 times. With a larger sample size, the experimental and theoretical probabilities should converge closer to each other.
The relative frequency of selecting each field trip can be calculated by dividing the number of times each trip was selected by the total number of spins, and then multiplying by 100 to express it as a percentage. For example, the relative frequency of selecting Field Trip A is (8/50) x 100 = 16%, the relative frequency of selecting Field Trip B is (16/50) x 100 = 32%, and so on.
Based on the data, Field Trip B appears to be the most popular, as it was selected the most number of times (16 times out of 50 spins).
To know more about frequency visit:
https://brainly.com/question/254161
#SPJ1
Commplete Question:
A science teacher uses a fair spinner to simulate choosing one of five different field trips for her classes. The spinner has 5 equal sections, each representing a different trip. The teacher spins the spinner 50 times and records the results in the table below:
Field Trip Number of times selected
A 8
B 16
C 9
D 12
E 5
Apply math models to analyze the data and answer the following questions:
What is the experimental probability of selecting each field trip?
What is the theoretical probability of selecting each field trip?
Do the experimental and theoretical probabilities match? If not, what could be the reason for the difference?
What is the relative frequency of selecting each field trip?
Based on the data, which field trip appears to be the most popular?
The table and corresponding image show the proof of the relationship
between the slopes of two parallel lines. What is the missing statement in
step 4?
A. c-d=b-a
B. b-c=d-a
OC. c-0=a-b
OD. d-0=8-a
Answers
Option A. c - 0 = b - a is the missing statement in Step 4 of the proof.
To determine the missing statement in Step 4 of the proof, let's examine the given table and image related to the relationship between the slopes of two parallel lines.
Step 1: Given the slopes of two parallel lines, m₁ and m₂.
Step 2: Assume two points on each line: (0, a) and (c, b).
Step 3: Calculate the slopes using the slope formula: m₁ = (b - a) / (c - 0) and m₂ = (d - a) / (0 - c).
Step 4: ??? (Missing Statement)
Step 5: Since the lines are parallel, the slopes are equal, so m₁ = m₂.
By analyzing the given information, we can identify the missing statement by comparing the calculated slopes:
From Step 3, we have:
m₁ = (b - a) / (c - 0)
m₂ = (d - a) / (0 - c)
Comparing the two slopes, we can see that (b - a) / (c - 0) = (d - a) / (0 - c).
To express this relationship, the missing statement in Step 4 should be:
A. c - 0 = b - a
For similar question on missing statement.
https://brainly.com/question/30113873
#SPJ8
there are 50 people in a coffee shop fourteen are tourist.what percent of people in the shop are tourist and non tourist
Answers
Answer:
tourist: 28%
non-tourist: 72%
Step-by-step explanation:
total: 50
tourists: 14
non-tourists:50 - 14 = 36
tourist percentage: 14/50 × 100% = 28%
non-tourist percentage: 36/50 × 100 = 72%
x⁵+x³-5 is divided by x-2
Answers
The Polynomial x⁵ + x³ - 5 is divided by x - 2, the quotient is x⁴ + 3x³ + 6x² + 12x + 24, and the remainder is 48.
The quotient and remainder when the polynomial x⁵ + x³ - 5 is divided by x - 2, we can use polynomial long division. Here's the step-by-step process:
1. Write the dividend (x⁵ + x³ - 5) and the divisor (x - 2).
x - 2 | x⁵ + x³ + 0x² + 0x - 5
2. Divide the first term of the dividend (x⁵) by the first term of the divisor (x) to get x⁴. Write x⁴ above the line. x⁴
x - 2 | x⁵ + x³ + 0x² + 0x - 5
3. Multiply the divisor (x - 2) by the quotient term (x⁴) to get x⁵ - 2x⁴. Write this under the dividend and subtract it. x⁴
x - 2 | x⁵ + x³ + 0x² + 0x - 5
- (x⁵ - 2x⁴)
3x⁴ + 0x³ + 0x² + 0x - 5
4. Bring down the next term (-5) from the dividend.
x⁴ + 3x³
x - 2 | x⁵ + x³ + 0x² + 0x - 5
- (x⁵ - 2x⁴)
3x⁴ + 0x³ + 0x² + 0x - 5
5. Divide the first term of the new dividend (3x⁴) by the first term of the divisor (x) to get 3x³. Write 3x³ above the line.
x⁴ + 3x³
x - 2 | x⁵ + x³ + 0x² + 0x - 5
- (x⁵ - 2x⁴)
3x⁴ + 0x³ + 0x² + 0x - 5
6. Multiply the divisor (x - 2) by the new quotient term (3x³) to get 3x⁴ - 6x³. Write this under the new dividend and subtract it.
x⁴ + 3x³
x - 2 | x⁵ + x³ + 0x² + 0x - 5
- (x⁵ - 2x⁴)
3x⁴ + 0x³ + 0x² + 0x - 5
- (3x⁴ - 6x³)
6x³ + 0x² + 0x - 5
7. Repeat steps 4-6 until you have subtracted all terms.
x⁴ + 3x³ + 6x² + 12x + 24
x - 2 | x⁵ + x³ + 0x² + 0x - 5
- (x⁵ - 2x⁴)
3x⁴ + 0x³ + 0x² + 0x - 5
- (3x⁴ - 6x³)
6x³ + 0x² + 0x - 5
- (6x³ - 12x²)
12x² + 0x + 0
- (12x² - 24x)
24x + 0
- (24x - 48)
48
8. The quotient is x⁴ + 3x³ + 6x² + 12x + 24, and the remainder is 48.
Therefore, when the polynomial x⁵ + x³ - 5 is divided by x - 2, the quotient is x⁴ + 3x³ + 6x² + 12x + 24, and the remainder is 48.
For more questions on Polynomial .
https://brainly.com/question/2833285
#SPJ8
Write an equation of the line perpendicular to line MN that goes through point Q.
Francisco has solved the problem for you, but made a mistake.
Find the error in the work and correct the mistake. Show your work for full credit.
Francisco’s work:
Step 1: Slope of MN: 1/4
Step 2: Slope of the line perpendicular: 4
Step 3: y - y = m(x - x) Q(6, -2)
y - (- 2) = 4 (x - 6)
Step 4: y + 2 = 4x - 24
Step 5: y + 2 - 2 = 4x - 24 - 2
Step 6: y = 4x - 26
Step completed incorrectly: ___
(I believe the step completed incorrectly is 2? But I’m not very sure on the showing my work part as well.)
Answers
Answer:
Step completed incorrectly: 2
Correct Answer: y = -4x + 22
Step-by-step explanation:
The graph is a straight line through points M(4, -1) and N(8, 0). Point Q is located at (6, -2).
To calculate the slope of the line, substitute the points into the slope formula:
\(\textsf{Slope $(m)$}=\dfrac{y_2-y_1}{x_2-x_1}=\dfrac{0-(-1)}{8-4}=\dfrac{1}{4}\)
Therefore, the slope of MN is 1/4, so step 1 of Francisco's calculations is correct.
If two lines are perpendicular to each other, the slopes of these lines are negative reciprocals. The negative reciprocal of a number is its negative inverse.
The negative reciprocal of 1/4 is -4.
Therefore, the slope of the perpendicular line is -4.
So Francisco has made an error in his calculation in step 2 by not making the perpendicular slope negative.
Corrected work
\(\textsf{Step 1:} \quad \sf slope\;of\;MN:\; \dfrac{1}{4}\)
\(\textsf{Step 2:} \quad \sf slope\;of\;the\;line\;perpendicular:\; -4\)
\(\begin{aligned}\textsf{Step 3:} \quad y-y_1&=m(x-x_1)\;\; \sf Q(6,-2)\\y-(-2)&=-4(x-6)\end{aligned}\)
\(\textsf{Step 4:} \quad y+2=-4x+24\)
\(\textsf{Step 5:} \quad y+2-2=-4x+24-2\)
\(\textsf{Step 6:} \quad y=-4x+22\)
Therefore, step 2 has been completed incorrectly.
The correct answer is y = -4x + 22.

What point lies on the graph y=x2-5
Answers
The point (0, -5) lies on the graph of the quadratic equation y = x² - 5. The shape of the graph is a parabola.
How to solve an equation?An equation is an expression containing numbers and variables linked together by mathematical operations such as addition, subtraction, division, multiplication and exponents.
The equation y = x² - 5 represents a quadratic equation. A quadratic equation have the shape of a parabola.
When x = 0;
y = 0² - 5
y = -5
The point (0, -5) lies on the graph of y = x² - 5
Find out more on equation at: https://brainly.com/question/25841119
#SPJ1

which expression below is equal to -18 -8(2)+5_8+2(-5)_8+2(5)-8(5)+2
Answers
- 8 + 2(- 5)
- 8 - 10
= - 18
The correct answer is the second option
List all the subsets of the given set.
{e, n, t}
Answers
The subsets of the set {e, n, t} are given as follows:
{{}, {e}, {n}, {t}, {e,n}, {e,t}, {n,t}, {e,n,t}}.
How to obtain the number of subsets in a set?Considering a set with n elements, the number of subsets in the set is the nth power of 2, that is:
\(2^n\)
The set for this problem is given as follows:
{e, n, t}
The cardinality is given as follows:
n = 3.
Hence the number of subsets is given as follows:
2³ = 8.
The subsets are given as follows:
{{}, {e}, {n}, {t}, {e,n}, {e,t}, {n,t}, {e,n,t}}.
In which {} is the empty set.
More can be learned about the subsets of a set at brainly.com/question/13458417
#SPJ1
Please help me the question

Answers
The polynomials completely factorized have the following expressions;
50). x³ - 3x² - 26x - 12 = (x - 6)(x + 1)(x + 2)
51). x³ - 12x² + 12x + 80 = (x - 10)(x + 2)(x - 4)
52). x³ - 18x² + 95x + 126 = (x - 9)(x - 2)(x - 7)
53). x³ - x² + 21x + 45 = (x + 5)(x - 3)(x - 3)
How to factorise the polynomials completelyFor the polynomial x³ - 3x² - 26x - 12 divisible by x - 6;
(x³ - 3x² - 26x - 12)/(x - 6) = x² + 3x + 2
x² + 3x + 2 = (x + 1)(x + 2)
so;
x³ - 3x² - 26x - 12 = (x - 6)(x + 1)(x + 2)
For the polynomial x³ - 12x² + 12x + 80 divisible by x - 10;
(x³ - 12x² + 12x + 80)/(x - 10) = x² - 2x - 8
x² - 2x - 8 = (x + 2)(x - 4)
so;
x³ - 12x² + 12x + 80 = (x - 10)(x + 2)(x - 4)
For the polynomial x³ - 18x² + 95x + 126 divisible by x - 9;
(x³ - 12x² + 12x + 80)/(x - 9) = x² - 9x + 14
x² - 9x + 14 = (x - 2)(x - 7)
so;
x³ - 18x² + 95x + 126 = (x - 9)(x - 2)(x - 7)
For the polynomial x³ - x² + 21x + 45 divisible by x + 5;
(x³ - x² + 21x + 45)/(x + 5) = x² - 6x + 9
x² - 6x + 9 = (x - 3)(x - 3)
so;
x³ - x² + 21x + 45 = (x + 5)(x - 3)(x - 3)
Therefore, by complete factorization the expressions (x - 6)(x + 1)(x + 2), (x - 10)(x + 2)(x - 4), (x - 9)(x - 2)(x - 7), and (x + 5)(x - 3)(x - 3) are the factors of their respective polynomial.
Read more about polynomial here:https://brainly.com/question/8021175
#SPJ1
The revenue, in thousands of dollars, of a new flavor of liquor is given below as function of the number of gallons (in hundreds), x, sold:
\(r(x) = 50x - {x}^{2} \)
What is the maximum revenue? Use units
Answers
Answer:
$625,000
Step-by-step explanation:
The maximum revenue will be found where the derivative of the revenue function is zero.
r'(x) = 50 -2x = 0
50 = 2x
x = 25
When 2500 gallons are sold, the revenue is ...
r(25) = 50(25) -25(25) = (50 -25)(25) = 25(25) = 625 . . . thousands
The maximum revenue is $625,000.
What is the perimeter of rectangle EFGH?
Answers
Answer:
But where are the rectangles??
A bag contains 10 green,8 blue, and 2 white balls. Naomi seclets 2 balls from the bag at random, one at a time, without replacing them. What is the probability that she selects all two white balls?
E.) 2/95
F.) 1/95
G.) 1/190
H.) 1/380
Answers
To find the probability that Naomi selects both white balls, we need to consider the total number of possible outcomes and the number of favorable outcomes.
Total number of outcomes:
Naomi selects 2 balls without replacement, so the total number of outcomes is the number of ways she can choose 2 balls out of the total number of balls in the bag. This can be calculated using combinations:
Total outcomes = C(20, 2) = (20!)/(2!(20-2)!) = (20 * 19)/(2 * 1) = 190
Number of favorable outcomes:
Naomi needs to select 2 white balls. There are 2 white balls in the bag, so the number of favorable outcomes is the number of ways she can choose 2 white balls out of the 2 white balls in the bag:
Favorable outcomes = C(2, 2) = 1
Probability = Favorable outcomes / Total outcomes = 1/190
Therefore, the correct answer is (G) 1/190.
7.
Find all solutions to the following triangle. (Round your answers for angles A, C, A', and to the nearest minute. Round your answers for sides a and a'to two decimal places. If either triangle is not
possible, enter NONE In each corresponding answer blank.)
B = 65° 20', b = 5.38 inches, c = 4.88 inches
First triangle (assume C greater than or equal to 90°):
A= ____ degrees ____’
C=____ degrees ____’
a= ____ in
Answers
The measures of the angles and the lengths of the sides of the triangle can
be found using sine rule.
The correct responses are;
A = 59 degrees 9'C = Nonea = 5.083 in.Reasons:
The given parameter are;
∠B = 65°20', b = 5.38 inches, c = 4.88 inches
∠C ≥ 90°
By sine rule, we have;
\(\dfrac{5.38}{sin(65^{\circ} 20')} = \mathbf{ \dfrac{4.88}{sin(\angle C)}}\)
\(sin(\angle C) = \mathbf{ \dfrac{sin(65^{\circ} 20') \times 4.88}{5.38}}\)
\(\angle C = arcsin \left(\dfrac{sin(65^{\circ} 20') \times 4.88}{5.38} \right) \approx \mathbf{ 55.517 ^{\circ}}\)
∠C = 55.517° < 90°, therefore, the correct response is; None
\(\dfrac{sin(65^{\circ} 20')}{5.38} = \dfrac{4.88}{sin(\angle C)}\)
∠A = 180° - 65°20' - 55.517° = 59.15° = 59°9'
∠A = 59°9'
Therefore;
\(\dfrac{5.38}{sin(65^{\circ} 20')} = \mathbf{ \dfrac{a}{sin(59.15^{})}}\)
\(a = \dfrac{5.38 \times sin(59.15^{\circ}) }{sin(65^{\circ} 20')} \approx \mathbf{ 5.083}\)
a ≈ 5.083 inches
Learn more here:
https://brainly.com/question/15018190
A CEO of Awesome Coolers owns 10 pairs of pants, 7 shirts, 3 ties and 5 jackets. How many different outfits can he wear to the office if he must wear one of each item?
Answers
The number of outfits that the CEO can wear to his office would be = 1050
What is combination?Combination can be defined as the number of possible arrangements that can be gotten from a number of a given value of item.
From the question,
The number of pairs of pants owned by the CEO = 10
The number of shirts owned by the CEO= 7
The number of ties owned by the CEO = 3
The number of jackets owned by CEO = 5
Therefore the different types of outfit that the CEO can wear to the office = 10×7×3×5 = 1050
Learn more about combination here:
https://brainly.com/question/26852614
#SPJ1
QUICK ANSWER WILL GIVE BRAINLIEST AND 100 POINTS:
Explain the following in complete sentences:
How is the base of a rectangular pyramid related to the lateral faces?
Answers
Answer:
the base of a lateral pyramid is related to lateral faces because though it is not a lateral face itself is connected to the sides of the pyramid and the side of the pyramid is connected to the vertex of the shape
Step-by-step explanation:
the base of a lateral pyramid is related to lateral faces because though it is not a lateral face itself is connected to the sides of the pyramid and the side of the pyramid is connected to the vertex of the shape
Answer:
The net of a triangular pyramid with an equilateral triangle for the base consists of four triangles, and at least three are congruent.
Step-by-step explanation:
I just got born again I'm a Christian
What is thirty-five and seven thousandths in decimal?
Answers
Answer:
Question: What is thirty-five and seven thousandths in decimal?
Answer: is 35.007
NO LINKS!!! URGENT HELP PLEASE!!!
Solve ΔABC using the Law of Sines
1. A = 29°, C = 63°, c = 24
2. A = 72°, B= 35°, c = 21
Answers
Answer:
1) B = 88°, a = 13.1, b = 26.9
2) C = 73°, a = 20.9, b = 12.6
Step-by-step explanation:
To solve for the remaining sides and angles of the triangle, given two sides and an adjacent angle, use the Law of Sines formula:
\(\boxed{\begin{minipage}{7.6 cm}\underline{Law of Sines} \\\\$\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}$\\\\\\where:\\ \phantom{ww}$\bullet$ $A, B$ and $C$ are the angles. \\ \phantom{ww}$\bullet$ $a, b$ and $c$ are the sides opposite the angles.\\\end{minipage}}\)
Question 1Given values:
A = 29°C = 63°c = 24As the interior angles of a triangle sum to 180°:
\(\implies A+B+C=180^{\circ}\)
\(\implies B=180^{\circ}-A-C\)
\(\implies B=180^{\circ}-29^{\circ}-63^{\circ}\)
\(\implies B=88^{\circ}\)
Substitute the values of A, B, C and c into the Law of Sines formula and solve for sides a and b:
\(\implies \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\)
\(\implies \dfrac{a}{\sin 29^{\circ}}=\dfrac{b}{\sin 88^{\circ}}=\dfrac{24}{\sin 63^{\circ}}\)
Solve for a:
\(\implies \dfrac{a}{\sin 29^{\circ}}=\dfrac{24}{\sin 63^{\circ}}\)
\(\implies a=\dfrac{24\sin 29^{\circ}}{\sin 63^{\circ}}\)
\(\implies a=13.0876493...\)
\(\implies a=13.1\)
Solve for b:
\(\implies \dfrac{b}{\sin 88^{\circ}}=\dfrac{24}{\sin 63^{\circ}}\)
\(\implies b=\dfrac{24\sin 88^{\circ}}{\sin 63^{\circ}}\)
\(\implies b=26.9194211...\)
\(\implies b=26.9\)
\(\hrulefill\)
Question 2Given values:
A = 72°B = 35°c = 21As the interior angles of a triangle sum to 180°:
\(\implies A+B+C=180^{\circ}\)
\(\implies C=180^{\circ}-A-B\)
\(\implies C=180^{\circ}-72^{\circ}-35^{\circ}\)
\(\implies C=73^{\circ}\)
Substitute the values of A, B, C and c into the Law of Sines formula and solve for sides a and b:
\(\implies \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\)
\(\implies \dfrac{a}{\sin 72^{\circ}}=\dfrac{b}{\sin 35^{\circ}}=\dfrac{21}{\sin 73^{\circ}}\)
Solve for a:
\(\implies \dfrac{a}{\sin 72^{\circ}}=\dfrac{21}{\sin 73^{\circ}}\)
\(\implies a=\dfrac{21\sin 72^{\circ}}{\sin 73^{\circ}}\)
\(\implies a=20.8847511...\)
\(\implies a=20.9\)
Solve for b:
\(\implies \dfrac{b}{\sin 35^{\circ}}=\dfrac{21}{\sin 73^{\circ}}\)
\(\implies b=\dfrac{21\sin 35^{\circ}}{\sin 73^{\circ}}\)
\(\implies b=12.5954671...\)
\(\implies b=12.6\)
The side length of an equilateral triangle is 4X +2 which expression represents the perimeter of the triangle
Answers
Answer:
12x + 6
Step-by-step explanation:
perimeter equals the sum of all sides
if each side is 4x+2 then 3(4x+2) = 12x+6
Maths question help pls !!!!!

Answers
Given that the coordinates of the points A and B are ( -6, - 9) and ( -4, - 9) respectively. What are the coordinates of the midpoint of AB?
A ( -2, 0)
B ( - 5, - 9)
C ( 5, 9 )
D ( -10, - 18)
Answers
Answer:
B
Step-by-step explanation:
The midpoint formula is \((\frac{x1+x2}{2} ,\frac{y1+y2}{2} )\)
Lets plug in our points:
\(\frac{(-6)+(-4)}{2}\)=-5 (the x value)
\(\frac{(-9)+(-9)}{2}\)=-9 (the y value)
What is the simplified form of the following expression
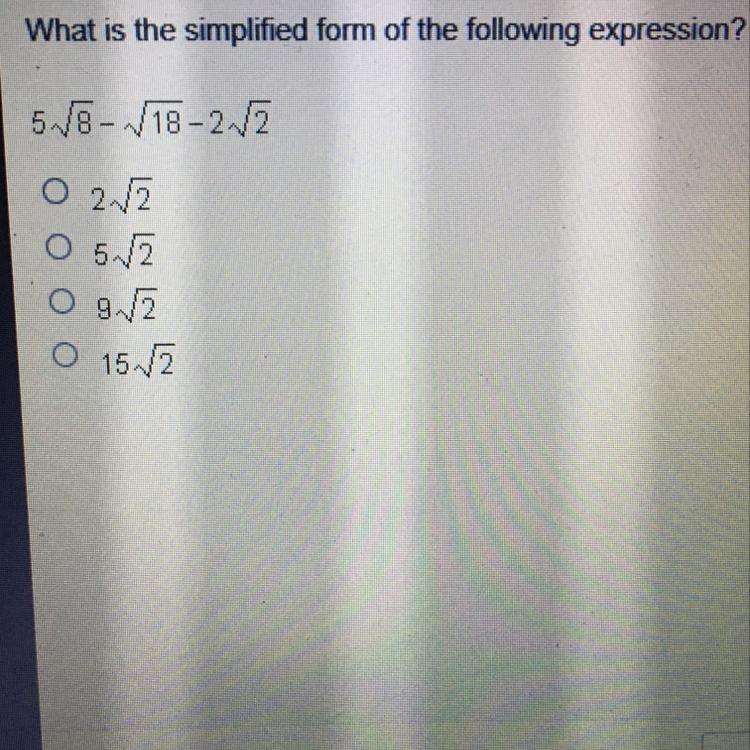
Answers
Point A is the original point before rotating. Which point represents A′ after A(4, 1) is rotated 90° counterclockwise: B, C, D, E, F, G, or H?

Answers
Answer:
Point G
Step-by-step explanation:
The mapping rule for a 90° counterclockwise rotation is:
(x, y) → (-y, x)
Therefore, if A = (4, 1):
A' = (-1, 4)The point that represents A' after A(4, 1) is rotated 90° counterclockwise is:
Point G
Sarah lives in Ruthin and works in Oswestry for 5 days a week. each day she travel to and from work. Work how many miles does she commute a week
Answers
Answer: 330 miles
Step-by-step explanation:
The distance provided for the question is:
Wrexham
18 Ruthin
21 12 Cornwen
15 33 23 Oswestry
What this means is that Ruthin and Oswestry are 33 miles apart.
Each day, Jane travels back and forth for a total of:
= 33 * 2
= 66 miles
In 5 days she would have travelled:
= 5 * 66
= 330 miles
The model shows the expression 219 Which expression is equivalent to this sum? O 3(7+3) O 307)+ 3 O 3+7+3 O 7(3+3) Mark this and retum Me
Answers
Answer:
a
Step-by-step explanation:
A 2-quart carton of yogurt costs $5.36. What is the price per cup?
need correct answer.
Answers
The price per cup when a 2-quart carton of yogurt costs $5.36 is $0.67.
How to illustrate the word problem?A word problem in mathematics simply refers to a question that is written as a sentence or in some cases more than one sentence which requires an individual to use his or her mathematics knowledge to solve the real.life scenario given.
In this case, a 2-quart carton of yogurt costs $5.36. It should be noted that 1 quart = 4 cups.
Therefore, 2 quarts will be:
= 2 × 4.
= 8 cups
Therefore, the price per cup will be:
= $5.36 / 8
= $0.67
Learn more about word problem on:
brainly.com/question/21405634
#SPJ1