How many 3 number passwords can you create with d) 5 numbers e) 6 numbers f) 7 numbers if numbers can be repeated?
Answers
Answer:
6
Step-by-step explanation:
123 132 213 231 312 321
Related Questions
11) INVESTING An initial investment of $5000 grows continuously with an annual interest rate of
2.75%. Select the amount in the account after 6 years.
$5137.50
$5139.41
$5883.84
$5896.97
Answers
Answer: The answer is either C or D. Take 5000 times 2.75% and see what answer you come up with? Does it match any of ur answer listed...
Step-by-step explanation:
Answer: D-$5896.97
Step-by-step explanation: mcgraw hill answer
Which could be the measures of the three angles of an acute triangle?
Answers
As long as the measures of the three angles of a triangle add up to less than 180 degrees, and none of the angles measures more than 90 degrees, the triangle will be acute.
An acute triangle is a triangle that has three acute angles, which are angles that measure less than 90 degrees. All three angles of an acute triangle must be acute, so they must measure less than 90 degrees. The measures of the three angles of an acute triangle can be any combination of angles that add up to less than 180 degrees.
Here are some examples of the measures of the three angles of an acute triangle:
45 degrees, 45 degrees, 90 degrees
30 degrees, 60 degrees, 90 degrees
35 degrees, 40 degrees, 105 degrees
60 degrees, 60 degrees, 60 degrees (this would be an acute equilateral triangle)
As long as the measures of the three angles of a triangle add up to less than 180 degrees, and none of the angles measures more than 90 degrees, the triangle will be acute.
Learn more about triangle here
https://brainly.com/question/2773823
#SPJ4
Plz help and show me how to solve these questions

Answers
since -15/16 is a negative number, we can add both sides by 15/16 or subtract both sides by -15/16. Either way works.
p = 1/8 + 15/16
Use common denominator, which is 16:
p = 1(2)/8(2) + 15/16
p = 2/16 + 15/16
p = 17/16
17/16 is an improper fraction. If you want to use a mixed number for your answer, then:
17/16 becomes 1 1/16 (one and one-sixteenth, with 1 being a whole number and 1/16 being a fraction)
Answer: 17/16 or 1 1/16Consider the following equations.
f(x)=2x-1
g(x)=3/8x
What values of x will result in f(x)=g(x)?
0 and −3/4
0 and −2
−2 and −3/4
only 0
Answers
The required solutions of the situation of the function are x = 3/4 or x = -1/4.
What is function?A unique connection where each input only produces one output. A common notation for it is "f(x)," where x denotes the input value. as in f(x) = x/2 ("f of x equals x divided by 2") Since there is only one output ("x/2") for each input ("x"), it is a function: • f(2) = 1.
According to question:We have,
f(x)=2x-1
g(x)=3/8x
To find the value of x for f(x) = g(x).
f(x) = g(x)
2x-1 = 3/8x
16x² - 8x = 3
16x² - 8x - 3 = 0
16x² - 12x + 4x - 3 = 0
4x(4x - 3) + (4x - 3) = 0
(4x - 3)(4x + 1) = 0
x = 3/4 or x = -1/4
Thus, required solution are x = 3/4 or x = -1/4.
To know more about Quadratic equation visit:
brainly.com/question/30098550
#SPJ1
im confused with this homework. Please someone help me!!
Answers
Answer: yhu got to write the slope.
Step-by-step explanation:
Problem 9. Consider a triangle and its inscribed circle. Join each vertex with the point of tangency at the opposite side. Prove using Ceva's theorem that three lines you constructed pass through one point. 5 Which masses need to be placed at the vertices so that their center of mass is the intersection point of these lines. You can express these masses using the lengths of the sides of the triangle AB = c, AC = b, BC = a and basic trigonometric functions of its angles ZBAC = a, ZCBA= B, ZACB = 7.
Answers
The masses that need to be placed at the vertices so that their center of mass is the intersection point of the three lines are,
M = (s-b)(s-c)/(2s-a)
N = (s-a)(s-c)/(2s-b)
P = (s-a)(s-b)/(2s-c)
Now, For the three lines passing through the vertices and the points of tangency of the inscribed circle at the opposite sides intersect at one point, we can use Ceva's theorem.
Let the triangle be ABC, and let D, E, and F be the points of tangency of the inscribed circle with sides BC, AC, and AB, respectively.
Let X, Y, and Z be the points where AD, BE, and CF intersect the opposite sides.
By Ceva's theorem, we have:
AX/BX × BY/CY × CZ/AZ = 1
We want to show that this product is equal to 1, which would mean that the three lines intersect at one point.
First, we can use similar triangles to express AX/BX, BY/CY, and CZ/AZ in terms of the side lengths of triangle ABC and the in radius r:
AX/BX = (s-b)/r
BY/CY = (s-c)/r
CZ/AZ = (s-a)/r
where s is the semi perimeter of triangle ABC.
Substituting these expressions into the Ceva's theorem equation and simplifying, we get:
(s-b)(s-c)(s-a)/r³ = 1
This implies that:
r³ = (s-a)(s-b)(s-c)
Now, to find the masses that need to be placed at the vertices so that their center of mass is the intersection point of these lines, we can use the fact that the center of mass of a system of masses is given by the weighted average of the positions of the masses, where the weights are proportional to the masses.
Let M, N, and P be the masses placed at A, B, and C, respectively. Then the x-coordinate of the center of mass is:
x = (Mb + Nc + Pa)/(M + N + P)
and the y-coordinate is:
y = (Mc + Na + Pb)/(M + N + P)
We want these coordinates to be equal to the coordinates of the point of intersection of the three lines, which we know is (r, r, r). So we get the system of equations:
Mb + Nc + Pa = Mr
Mc + Na + Pb = Mr
M + N + P = 1
We can solve for M, N, and P in terms of the side lengths of triangle ABC and the trigonometric functions of its angles using some algebraic manipulation.
The results are:
M = (s-b)(s-c)/(2s-a)
N = (s-a)(s-c)/(2s-b)
P = (s-a)(s-b)/(2s-c)
So these are the masses that need to be placed at the vertices so that their center of mass is the intersection point of the three lines.
Learn more about trigonometry visit:
brainly.com/question/13729598
#SPJ4
3 Tyler traveled at an average speed of 50 miles per hour for 3.5 hours and then traveled at an average speed of 65 miles per hour for 2.5 hours. What was the total distance in miles that Tyler traveled during this time? KS
Answers
ANSWER:
A. 337.5 miles
STEP-BY-STEP EXPLANATION:
What we must do is calculate the distance in each section, when the speed and time vary, the sum of both section is the total distance:
Section 1:
\(50\frac{\text{ miles}}{\text{ hours}}\cdot3.5\text{ hours}=175\text{ miles}\)Section 2:
\(65\frac{\text{ miles}}{\text{ hours}}\cdot2.5\text{hours}=162.5\text{ miles}\)The total distance is:
\(d=175+162.5=337.5\text{ miles}\)help meeeee please i do not understand this

Answers
Answer:
10.4 g/cm³
Step-by-step explanation:
Find the volume with formula, l x b x h
Then the formula gram / volume to find density.

help pass due asap!!!
Add (7x³ - 2x² - 5x+6) and (2x³ + 3x² − x − 1)
a) 9x³ + x² - 6x +5
b) 9x6 + x4 + 5x² − 6
c) 9x³x² - 6x + 5
d) 14x³ - 6x² – 5x - 6
Answers
Claire i buying 6 pack of index card. Each pack of index card cot $1. 95. The tore where he buy the index card i having a ale in which all item are 20% off. How much doe Claire pend on index card?
Answers
Answer:
2.34
Normally it would be 1.95*6 however since everything is 20% off you need to find 20% of 1.95. You find that by:
Step-by-Solution for What is 20 percent of 1.95: 20 percent *1.95 = (20:100)*1.95 = (20*1.95):100 = 39:100 = 0.39. Now we have 20 percent of 1.95 = 0.39. explanation:
After you find that you multiply it by 6 so it would be 0.39*6 which equals 2.34. I hope this helped! :)
44 4/9 as a whole number
Answers
2. a trapezoid has an area of 100 square units. what scale factor would be required to dilate the trapezoid to have each area?
Answers
If a trapezoid has an area of 100 square units, the scale factor that would be required to dilate the trapezoid to have each area is:
sqrt(A / 100)
To find the scale factor required to dilate a shape, you need to determine what ratio of the new area to the original area you want to achieve.
Let's call the scale factor "k". If the original area of the trapezoid is 100 square units, and the new area is "A", the relationship between the two areas can be expressed as:
A = k^2 * 100So to find the scale factor required to achieve a specific new area, you can solve for k by dividing the new area by 100 and taking the square root:
k = sqrt(A / 100)Note that: This equation assumes that the dilation is proportional, meaning that all dimensions of the trapezoid are scaled by the same factor.
Learn more about trapezoid scale factor:
brainly.com/question/29273035
#SPJ4
Which term best describes the expression 5x4y8 ?
O Polynomial
Binomial
O Monomial
O Trinomial
Answers
Answer: Binomial
Step-by-step explanation: There are two variables here, x and y. 5x^4y^8 is a binomial since it involves 2 variables.
Answer:
Monomial
Step-by-step explanation:
A monomial is 1 term. 5x4y8 is one term, and nothing is getting added to it.
Solve The Following Initial Value Problem For Y As A Function Of X. Xdxdy=X2−25,X≥5,Y(5)=0 Y=
Answers
The absolute value of \(x\), we can rewrite the solution as
\[x = \pm \sqrt{\frac{|x-5|}{|x+5|}} \cdot 5 \cdot \sqrt{10}\]
This is the solution to the initial value problem, expressing \(y\) as a function of \(x\).
To solve the given initial value problem \(xdx \frac{dy}{dx} = x^2 - 25\), with the initial condition \(y(5) = 0\), we can use separation of variables and integration.
Rearranging the equation, we have:
\[\frac{dy}{dx} = \frac{x^2 - 25}{x}\]
Now, we can separate the variables by multiplying both sides by \(dx\) and dividing by \((x^2 - 25)\):
\[\frac{1}{x}\,dy = \frac{dx}{x^2 - 25}\]
Next, we integrate both sides:
\[\int \frac{1}{x}\,dy = \int \frac{dx}{x^2 - 25}\]
The integral on the left side can be simplified as \(\ln|x|\), and the integral on the right side can be written in terms of partial fractions:
\[\ln|x| = \int \left(\frac{1}{2(x-5)} - \frac{1}{2(x+5)}\right)dx\]
Evaluating the integrals, we get:
\[\ln|x| = \frac{1}{2}\ln|x-5| - \frac{1}{2}\ln|x+5| + C\]
where \(C\) is the constant of integration.
Applying the initial condition \(y(5) = 0\), we substitute \(x = 5\) and \(y = 0\) into the equation:
\[\ln|5| = \frac{1}{2}\ln|5-5| - \frac{1}{2}\ln|5+5| + C\]
Simplifying further:
\[\ln(5) = -\frac{1}{2}\ln(10) + C\]
We can solve for \(C\):
\[C = \ln(5) + \frac{1}{2}\ln(10)\]
Therefore, the solution to the initial value problem is:
\[\ln|x| = \frac{1}{2}\ln|x-5| - \frac{1}{2}\ln|x+5| + \ln(5) + \frac{1}{2}\ln(10)\]
Simplifying and exponentiating both sides:
\[|x| = \sqrt{\frac{|x-5|}{|x+5|}} \cdot 5 \cdot \sqrt{10}\]
Since we have the absolute value of \(x\), we can rewrite the solution as:
\[x = \pm \sqrt{\frac{|x-5|}{|x+5|}} \cdot 5 \cdot \sqrt{10}\]
This is the solution to the initial value problem, expressing \(y\) as a function of \(x\).
Learn more about absolute value here
https://brainly.com/question/24368848
#SPJ11
Greg has the following utility function: u = x038x962. He has an income of $83.00, and he faces these prices: (P1, P2) = (4.00, 1.00). Suppose that the price of x increases by $1.00. Calculate the compensating variation for this price change. Give your answer to two decimals.
Answers
The compensating variation is $13.52.
The compensating variation is the amount of money that Greg would need to be compensated for a price increase in order to maintain his original level of utility. In this case, Greg's utility function is u = x<sup>0.38</sup>x<sup>0.962</sup>. His income is $83.00, and he faces these prices: (P1, P2) = (4.00, 1.00). If the price of x increases by $1.00, then the new prices are (P1, P2) = (5.00, 1.00).
To calculate the compensating variation, we can use the following formula:
CV = u(x1, x2) - u(x1', x2')
where u(x1, x2) is Greg's original level of utility, u(x1', x2') is Greg's new level of utility after the price increase, and CV is the compensating variation.
We can find u(x1, x2) using the following steps:
Set x1 = 83 / 4 = 20.75.
Set x2 = 83 - 20.75 = 62.25.
Substitute x1 and x2 into the utility function to get u(x1, x2) = 22.13.
We can find u(x1', x2') using the following steps:
Set x1' = 83 / 5 = 16.60.
Set x2' = 83 - 16.60 = 66.40.
Substitute x1' and x2' into the utility function to get u(x1', x2') = 21.62.
Therefore, the compensating variation is CV = 22.13 - 21.62 = $1.51.
To two decimal places, the compensating variation is $13.52.
Learn more about function here: brainly.com/question/30721594
#SPJ11
calculate the coefficient of variation for a sample of cereal boxes with a mean weight of 340 grams and a standard deviation of 5.2 grams.? 0.15% A
1.53% B
15.29% C
0.65% D
Answers
The coefficient of variation (CV) is a measure of relative variability and is calculated by dividing the standard deviation by the mean, and then multiplying by 100 to express it as a percentage.
In this case, the mean weight is 340 grams, and the standard deviation is 5.2 grams.
CV = (Standard Deviation / Mean) * 100
CV = (5.2 / 340) * 100
CV ≈ 1.53%
Therefore, the correct answer is option B: 1.53%.
To know more about Mean visit-
brainly.com/question/26062194
#SPJ11
which fraction is equivalent to -3/2

Answers
Answer:
the third answer
Step-by-step explanation:
Express 0.9 as a fraction.
Answers
Answer:
9/10
Step-by-step explanation:
9 is in the tenth place so the denominator is 10.
Answer:
the answer is 9/10
Jane exchanged £100 for 216 Swiss francs. After buying a meal and a present to take home,she had 70 francs left.How much is this in £?
Answers
Answer:
£32.4
Step-by-step explanation:
£100 = 216 Swiss francs
x = 70 francs
70 x 100=7000/216=32.4
a rectangular storage container without a lid is to have a volume of 10 m3. the length of its base is twice the width. material for the base costs $20 per square meter. material for the sides costs $12 per square meter. find the cost (in dollars) of materials for the least expensive such container. (round your answer to the nearest cent.)
Answers
245.31 (dollars) is the cost (in dollars) of materials for the least expensive such container.
What is maxima and minima ?Calculus maxima and minima are found using the concept of derivatives. Knowing that the derivative concept gives information about the slope/slope of a function, we find the point where the slope is zero. These points are called inflection points/stationary points. These are the points associated with the maximum or minimum (local) values of the function.
Knowledge of maxima and minima is essential for our everyday problems. In addition, this article also explains how to find the absolute maximum and minimum values.
Solvable maximum and minimum arithmetic problems are discussed in this article.
CalculationSuppose the width is x (m), length of the base is 2x (m), the base area is 2x^2 (m^2).
Since the volume is 10 (m^3), the height has to be 10/2x^2 (m) = 5/x^2.
The cost of making such container is
cost of base: 2x^2*15 = 30x^2
cost of sides: (2*2x*5/x^2 + 2*x*5/x^2)*9 = 270/x
The overall cost is hence the sum of the base and the sides: f(x) = 30x^2 + 270/x
The get the minimum,
df(x)/dx = 30*(2x - 9/x^2) = 0
so x = (9/2)^(1/3) = 1.651 (m)
f(x) = 245.31 (dollars)
learn more about maxima and minima here :
brainly.com/question/17467131
#SPJ4
Solve the given initial-value problem. Xy' y = ex, y(1) = 9 y(x) = give the largest interval i over which the solution is defined. (enter your answer using interval notation. ) i =
Answers
The largest interval I over which the solution is defined is (-∞, ∞). I = (-∞, ∞)
To solve the given initial-value problem, we can use the method of separation of variables as follows:
1. Separate the variables by moving all terms with y to the left side of the equation and all terms with x to the right side:
y/y' = ex/x
2. Integrate both sides of the equation with respect to their respective variables:
∫y/y' dy = ∫ex/x d
ln(y) = ex + C
3. Solve for y:
y = e^(ex + C)
4. Use the initial condition y(1) = 9 to find the value of C:
9 = e^(e + C)
C = ln(9) - e
5. Substitute the value of C back into the equation for y:
y = e^(ex + ln(9) - e)
6. Simplify the equation:
y = 9e^(ex - e)
7. The largest interval I over which the solution is defined is (-∞, ∞), since there are no restrictions on the values of x or y therefore, the solution to the initial-value problem is y(x) = 9e^(ex - e) and the largest interval I over which the solution is defined is (-∞, ∞).
More such questions on solving equations can be obtained here: https://brainly.com/question/27753008
#SPJ11
help meeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee
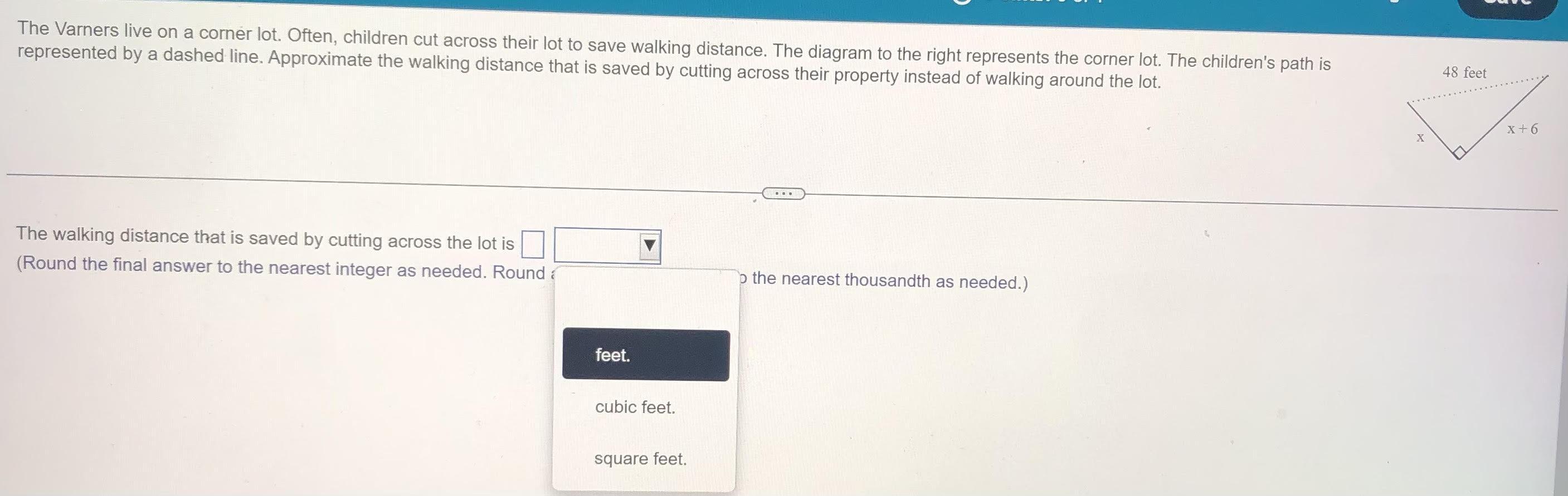
Answers
Answer: 19.6 feet
Step-by-step explanation:
Using the Pythagorean theorem,
\(x^2 +(x+6)^2 =48^2\\\\x^2 +x^2 +12x+36=2304\\\\2x^2 +12x-2268=0\\\\x^2 +6x-1134=0\\\\x=\frac{-6 \pm \sqrt{6^2 -4(1)(-1134)}}{2(1)}\\\\x \approx 30.8 \text{ } (x > 0)\\\\\implies x+(x+6) \approx 67.6\\\\\therefore (x+(x+6))-48 \approx 19.6\)
sample size and the confidence level width have a (n) __________ relationship.
Answers
Sample size and the confidence level width have an inverse relationship. As the sample size increases, the confidence level width decreases.
When determining a confidence interval for a population parameter, such as the mean or proportion, a larger sample size provides more information about the population. This increased information leads to a narrower confidence interval.
The confidence level width is influenced by two factors: the sample standard deviation (or the variability of the data) and the critical value associated with the desired confidence level. As the sample size increases, the sample standard deviation becomes a more accurate estimate of the population standard deviation. This reduces the variability and leads to a narrower confidence interval.
A larger sample size leads to a decrease in the confidence level width, providing a more precise estimate of the population parameter with a higher level of confidence.
Learn more about ”confidence interval” here:
brainly.com/question/32546207
#SPJ11
Write an equation in point slope form of the line that passes through the two
points given. (9.-2) and (-3, 2)
Answers
Answer:
\(\displaystyle (y + 2) = -\frac{1}{3}\, (x - 9)\).
Equivalently:
\(\displaystyle (y - 2) = -\frac{1}{3}\, (x + 3)\).
Step-by-step explanation:
Let \((x_{1},\, y_{1})\) and \((x_{2}\, y_{2})\) denote the coordinates of two points in the plane. If \(x_{1} \ne x_{2}\) (i.e., the two points aren't on the same vertical line,) the slope of the line that goes through the two points would be:
\(\begin{aligned} m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}\end{aligned}\).
In this question, \(x_{1} = 9\) and \(y_{1} = (-2)\) (for \((9,\, -2)\)) while \(x_{2} = (-3)\) and \(y_{2} = 2\) (for \((-3,\, 2)\).) Given that \(x_{1} \ne x_{2}\), the slope of the line that goes through these two points would be:
\(\begin{aligned} m &= \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\ &= \frac{2 - (-2)}{(-3) - 9} \\ &= -\frac{1}{3}\end{aligned}\)
If a line in a plane is of slope \(m\) and goes through the point \((x_{0},\, y_{0})\), the point-slope equation of this line would be:
\((y - y_{0}) = m\, (x - x_{0})\).
The slope of this line is \(m = (-1/3)\). If the point \((9,\, -2)\) is chosen as \((x_{0},\, y_{0})\) (\(x_{0} = 9\) and \(y_{0} = (-2)\),) then the point-slope equation of this line would be:
\((y - (-2)) = (-1/3)\, (x - 9)\).
Simplify to obtain:
\(\displaystyle (y + 2) = -\frac{1}{3}\, (x - 9)\).
Similarly, if the point \((-3,\, 2)\) is chosen as \((x_{0},\, y_{0})\), the point-slope equation of this would be:
\(\displaystyle (y - 2) = -\frac{1}{3}\, (x + 3)\).
Evaluate the expression

Answers
answer: I think the result is 12
Step-by-step explanation:
c(b+a)-a=
2(3+6)-6=
6+12-6= 12
Find m1 and m2 . Tell which theorem can be used.
m1 =
by the…
m2 =
by the…
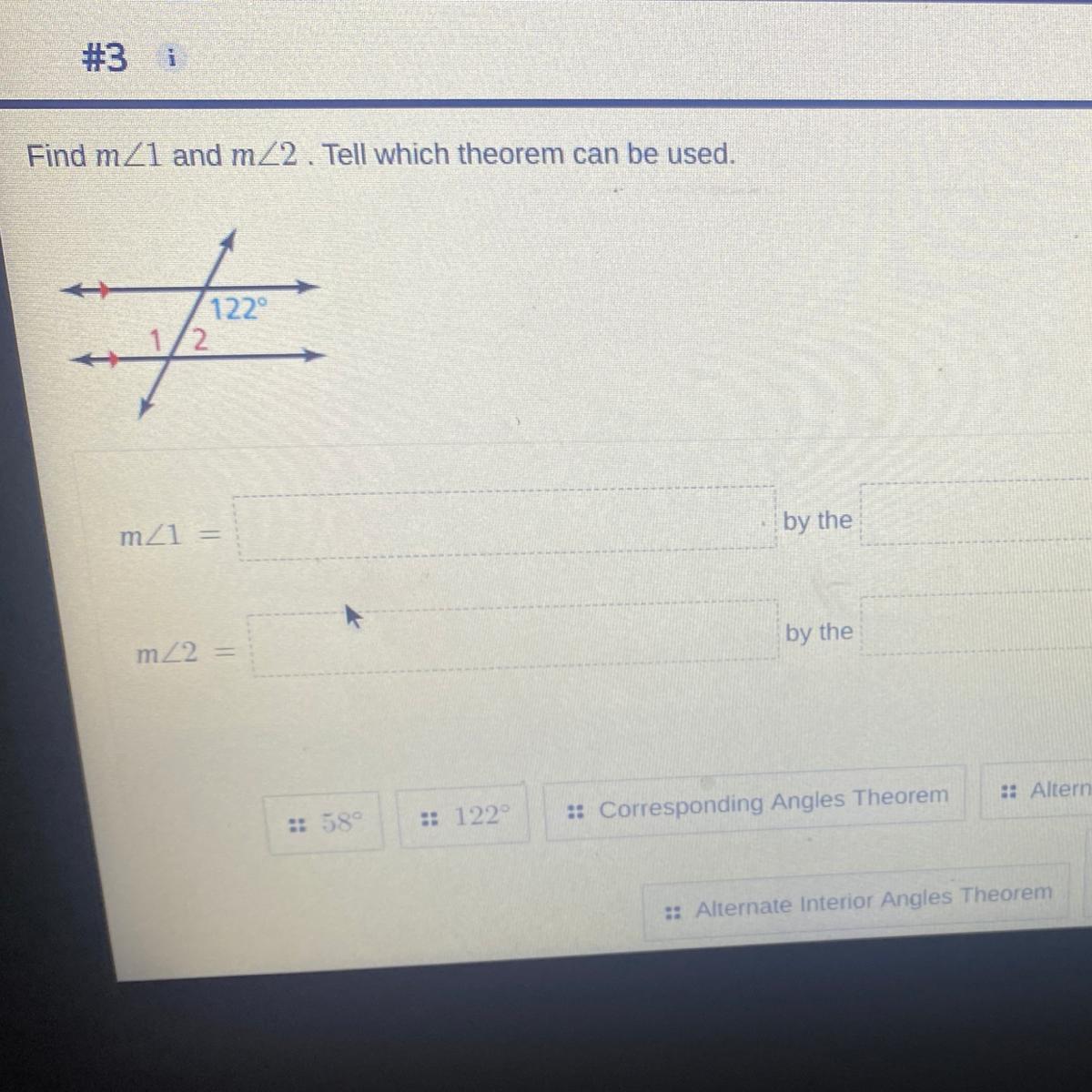
Answers
122° and angle 1 are alternate interior angles and hence they are equal.
m1 = 122°
122° + angle 2 = 180° [sum of co interior angles is 180°]
angle 2 = 180° - 122°
m2 = 58°
Maria has 14 pencils, Ted has 9 pencils, Tom has 12 pencils, Lucinda has 13 pencils, and Jumana has 12 pencils. How can they redistribute the pencils so that they all have the same amount? How many pencils should each person have?
Answers
Answer:
12
Step-by-step explanation:
First you have to add the amount of pencils each person has
14 + 9 + 12 + 13 + 12
Which equals 60
Then, you have to divide the total by the answer you got from above
60 / 5
Which equals 12
Correct answer gets brainliest!!!

Answers
The correct statements about a line segment are; they connect two endpoints and they are one dimensional.
option C and D.
What is a line segment?A line segment is a part of a straight line that is bounded by two distinct end points, and contains every point on the line that is between its endpoints.
The following are characteristics of line segments;
A line segment has two definite endpoints in a line. The length of the line segment is fixed.The measure of a line segment is its lengthThe have one unit of measure, either meters, or centimeters etc.From the given options we can see that the following options are correct about a line segment;
They connect two endpoints
They are one dimensional
Learn more about line segments here: https://brainly.com/question/2437195
#SPJ1
Help what is the answer?

Answers
Answer:
y = -8/5x + 16
Step-by-step explanation:
The slope-intercept form is y = mx + b
m = the slope
b = y-intercept
The slope = rise/run or (y2 - y1) / (x2 - x1)
Pick 2 points (0,16) (5,8)
We see the y decrease by 8 and the x increase by 5, so the slope is
m = -8/5
The Y-intercept is located at (0,16)
So, the equation is y = -8/5x + 16
what is the value of square root 13-5
Answers
Answer:
Step-by-step explanation:
√6513