how many arrangements of the letters of the word trigonal can be made if only two vowels and three continents are used
Answers
Using combinations, we know that we can have (B) 3600 arrangements of the word TRIGONAL using only 2 vowels and 3 constants.
What are combinations?A combination in mathematics is a choice made from a group of separate elements where the order of the selection is irrelevant. Combinations are mathematical operations that count the number of potential configurations for a set of elements when the order of the selection is irrelevant. You can choose the components of combos in any order. Permutations and combinations can be mixed up.So, the letter is: TRIGONAL
We know that we have to use:
2 vowels
3 constants
Then, we have:
2 vowels: 3C₂
3 constants: 5C₃
Ways to be arranged in: 5
3C₂ × 5C₃ × 5! = 3600
Therefore, using combinations, we know that we can have (B) 3600 arrangements of the word TRIGONAL using only 2 vowels and 3 constants.
Know more about combinations here:
https://brainly.com/question/28065038
#SPJ4
Complete question:
How many arrangements of the word TRIGONAL can be made if only two vowels and three consonants are used?
A) 6300 B) 3600
C) 6400 D) 7200
Related Questions
There are 60 species of animals at the Wiley Zoo that need a forest habitat. They make up 75% of the animals at the Wiley Zoo. How many species of animals are at the Wiley Zoo in all? Pick the model that represents the problem.
Answers
The total species of animals based on the information given is 80.
What is a percentage?A percentage is a value or ratio that may be stated as a fraction of 100. If we need to calculate a percentage of a number, we should divide it's entirety and then multiply it by 100. The percentage therefore refers to a component per hundred. Per 100 is what the word percent means. It is represented by %.
Let the number of species be represented by x.
This will be illustrated as:
75% × x = 60
0.75 × x = 60
0.75x = 60
Divide
x = 60 / 0.75
x = 80
The total species is 80.
Learn more about percentages on:
brainly.com/question/24877689
SPJ1
What is the value of the x-coordinate of the solution to the system of equations below?
y = 2x+8
y = -3x + 3
AND NO ITS NOT -1 I keep getting it wrong when I put -1 please I need helppp
Answers
I regret to inform you the answer is x = -1 :/
We can solve this three different ways.
First, because both equations are equal to variable y, we can set them equal to each other, isolate variables and constants, simplify, and then solve for x.
2x + 8 = -3x + 3
- 2x - 2x
8 = -5x + 3
-3 - 3
5 = - 5x
Divide both sides by -5
5 / (-5) = -5x / (-5)
-1 = x or x = -1
Second, we can isolate both variables x and y on one side and constants on the other and solve for x by adding and simplifying the system of equations.
y = 2x + 8
y = -3x + 3
2x - y = -8
3x - y = -3
Pick one of equations to multiply by -1 such that we can cancel out a variable and solve for the other.
2x - y = -8
-1(3x - y = -3)
2x - y = -8
3x + y = 3
Combine like terms
2x + 3x - y + y = -8 + 3
5x + 0 = -5
5x = -5
Divide both sides by 5
5x / 5 = (-5) / 5
x = -1
In this method, you could also solve for y and then plug it into one of the equations in order to solve for x.
The third way is to place both of these equations on a graph and observe where they cross paths. This image is included below. The first equation is represented by the red line; the second equation represented by the blue. As you can see, they intersect at point (-1, 6) where the x-value is -1 and the y-value is 6.
I suggest re-reading the question once more to see if it is, indeed, asking for the x-value or if these are the equations used. If it is, try possibly placing a space between the negative and the number 1. If this also does not work, consider screenshotting and reaching out to an instructor with the mistake in the system.

simplify
(3 − 6n5 − 8n4) − (−6n4 − 3n − 8n5)
Answers
Answer:
Simplify the expression.
2n⁵−2n⁴+3n+3
Express in the form 1 : n . Give n as a fully simplified fraction. 6 : 4
Answers
Answer:
3/2
Step-by-step explanation:
Given:
The given ratio is 6:4
To find:
The simplified fraction.
Solution:
Simple fraction is the rational number which is written in the form p/q ; where p = numerator, q = denominator and they both are integers.
Denominator can never be zero.
Simple fraction can also be called as Common or Vulgar fraction.
The given ratio can be written in the fractional form as follows:
6 : 4 = 6/4
Prime factorization of 6 : 2 x 3
Prime factorization of 4 : 2 x 2
6/4 = (2 x 3) / (2 x 2) [ Cancelling 2s]
= 3/2
Therefore, the fully simplest fraction of the given ratio 6:4 is 3/2.
What is the actual distance around the garden?It took Clare 30 minutes to walk around the garden at a constant speed
Answers
Answer:
f she walks for 30 minutes, that means she was traveling at about 280 feet per minute (8,400÷30=280), or about 16,800 feet per hour
Step-by-step explanation:
f(x) = x2 − x − ln(x)
(a) Find the interval on which f is increasing. (Enter your answer using interval notation.)
Find the interval on which f is decreasing. (Enter your answer using interval notation.)
(b) Find the local minimum and maximum value of f.
(c) Find the inflection point.
Answers
(a) The interval on which f is increasing: (0, ∞)
The interval on which f is decreasing: (0, 1)
(b) Local minimum: At x = 1, f(x) has a local minimum value of -1.
There is no local maximum value.
(c) Inflection point: At x ≈ 0.293, f(x) has an inflection point.
The function f(x) = x^2 - x - ln(x) is a quadratic function combined with a logarithmic function.
To find the interval on which f is increasing, we need to determine where the derivative of f(x) is positive. Taking the derivative of f(x), we get f'(x) = 2x - 1 - 1/x. Setting f'(x) > 0, we solve the inequality 2x - 1 - 1/x > 0. Simplifying it further, we obtain x > 1. Therefore, the interval on which f is increasing is (0, ∞).
To find the interval on which f is decreasing, we need to determine where the derivative of f(x) is negative. Solving the inequality 2x - 1 - 1/x < 0, we get 0 < x < 1. Thus, the interval on which f is decreasing is (0, 1).
The local minimum is found by locating the critical point where f'(x) changes from negative to positive. In this case, it occurs at x = 1. Evaluating f(1), we find that the local minimum value is -1.
There is no local maximum in this function since the derivative does not change from positive to negative.
The inflection point is the point where the concavity of the function changes. To find it, we need to determine where the second derivative of f(x) changes sign. Taking the second derivative, we get f''(x) = 2 + 1/x^2. Setting f''(x) = 0, we find x = 0. Taking the sign of f''(x) for values less than and greater than x = 0, we observe that the concavity changes at x ≈ 0.293. Therefore, this is the inflection point of the function.
Visit here to learn more about Inflection point:
brainly.com/question/30763521
#SPJ11
What is the value of x?
x + 5
X
X-2
x + 1

Answers
The most appropriate choice for Basic Proportionality Theorem will be given by -
x = 5 is the correct answer
What is Basic Proportionality Theorem?
If a line is drawn parallel to third side of a triangle, intersecting the other two sides of the triangle, the other two sides are divided in the same ratio.
Here,
In the figure, two parallel lines are given
By Basic Proportionality Theorem,
\(\frac{x}{x+5} = \frac{x-2}{x+1}\\\)
\(x(x +1) = (x - 2)(x + 5)\\x^2 +x = x^2 + 5x - 2x -10\\x = 3x -10\\3x - x = 10 \\ 2x = 10\\x = \frac{10}{2}\\x = 5\)
x = 5 is the correct answer
To learn more about Basic Proportionality Theorem, refer to the link-
https://brainly.com/question/14417137
#SPJ13
Patrick has $5300 in his college savings account. When he starts college, he withdraws $870 from his account every month. Based on this information, which equation best represents the relationship between the number of months, x, and the amount of money left in his savings account, y?
y=−870x+5300
y=870x−5300
y=5300870x
y=870x+5300
Answers
Answer:
its the second one y=870x-5300
Step-by-step explanation:
Question 20 of 40
Anna thinks of a number. She subtracts 5 from the number, multiplies the
result by 2, and then adds 6. The number she ends up with is 14. What
number did Anna start with?
If you work backward to solve this problem, what do you do first?
A. Divide 14 by 2
OB. Add 5 to 14
C. Subtract 5 from 14
D. Subtract 6 from 14
What’s the first steps when doing it backwards ?
Answers
Answer:
2(x-5)+6=14 is your starting equation, and then we solve:
2(x-5)+6=14
2(x-5)/2 +6=14/2
x-5+6=7
the first step is to divide by 2, so A :)))
Suppose the supply equation is Q=−2+P and the demand equation is given by Q=7− 0.5 where price is measured by dollars per unit.
(a) Find the effect of a $3 per unit subsidy on consumer surplus, producer surplus and total surplus.
(b) Suppose a price floor of $8 per unit is imposed. Find the effect of this price ceiling on CS,PS, and TS.
Answers
The $3 per unit subsidy will increase consumer surplus, decrease producer surplus, and increase total surplus. The $8 price floor will decrease consumer surplus, increase producer surplus, and decrease total surplus.
(a) To find the effect of a $3 per unit subsidy, we need to compare the equilibrium price and quantity before and after the subsidy. In the absence of the subsidy, the equilibrium price is determined by setting the demand equation equal to the supply equation:
7 - 0.5P = -2 + P
Solving for P, we find the equilibrium price P_eq = $5. The equilibrium quantity can be obtained by substituting this price back into either the supply or demand equation:
Q_eq = -2 + P_eq = -2 + 5 = 3 units
With the $3 per unit subsidy, the supply equation becomes Q = -2 + P - 3 = -5 + P. The new equilibrium price and quantity are determined by setting the demand equation equal to the new supply equation:
7 - 0.5P = -5 + P
Solving for P, we find P_subsidy = $6. The equilibrium quantity can be obtained by substituting this price back into the supply equation:
Q_subsidy = -5 + P_subsidy = -5 + 6 = 1 unit
To calculate the effects on consumer surplus (CS), producer surplus (PS), and total surplus (TS), we need to compare the areas of the relevant triangles. Before the subsidy, CS is the area above the demand curve and below the equilibrium price, PS is the area below the supply curve and above the equilibrium price, and TS is the sum of CS and PS. After the subsidy, CS expands, PS contracts, and TS increases.
(b) To find the effect of a $8 price floor, we need to compare the equilibrium price and quantity before and after the price floor. In the absence of the price floor, the equilibrium price and quantity remain the same as calculated in part (a): P_eq = $5 and Q_eq = 3 units.
With the $8 price floor, the market price cannot fall below $8. If the price floor is above the equilibrium price, it does not have any effect on the market. In this case, the price floor is below the equilibrium price, so it becomes binding. The new equilibrium price and quantity are determined by setting the supply equation equal to the price floor:
-2 + P_floor = 8
Solving for P_floor, we find P_floor = $10. The equilibrium quantity remains the same as Q_eq = 3 units.
To calculate the effects on CS, PS, and TS, we compare the areas of the relevant triangles. Before the price floor, CS is the area above the demand curve and below the equilibrium price, PS is zero because no units are being supplied, and TS is equal to CS. After the price floor, CS contracts, PS expands to include the entire area below the price floor and above the equilibrium quantity, and TS decreases.
In conclusion, the $3 per unit subsidy increases consumer surplus, decreases producer surplus, and increases total surplus. On the other hand, the $8 price floor decreases consumer surplus, increases producer surplus, and decreases total surplus. These effects can be visualized by comparing the areas of the relevant triangles in each scenario.
Learn more about total surplus here:
https://brainly.com/question/28557855
#SPJ11
Please help ASAP !!!!!!!

Answers
when group a loses an item or items to group b even though group a's population grew at a faster rate than group b's, the _______ paradox occurs.
Answers
When Group A loses an item or items to Group B even though Group A's population grew at a faster rate than Group B's, the Simpson's Paradox occurs.
This statistical anomaly happens when a trend appears in different groups of data, but disappears or reverses when the groups are combined. It is crucial to consider the context and variables involved when analyzing data, as the Simpson's Paradox may lead to incorrect conclusions if only aggregate data is examined.
This paradox serves as a reminder to always investigate the underlying factors that may influence statistical results.
Learn more about Simpson's paradox at
https://brainly.com/question/31679249
#SPJ11
Identify the slope from the equation: y = 13x-5
Answers
the given expression is'
y = 13x - 5
compare this equation with the standard equation
y = mx + c
here m is slope
so m = 13
thus, the slope of the equation is m = 13
the number of home runs hit per game for the millard girls' softball team are: 1, 2, 4, 3, 2, 4, 3, 0, 1, 2, 3, 5, 2, 1, and 5. a)what is the main number of home runs hit?
b) what is the median?
c) what is the mode?
Answers
(a) The main number of home runs hit per game is 2.6.
(b) The median number of home runs hit per game is 3.
(c) The mode(s) of the number of home runs hit per game are 2 and 3.
How to find main number of home runs hit?a) To find the main number of home runs hit, we need to calculate the mean of the data set.
Mean = (1+2+4+3+2+4+3+0+1+2+3+5+2+1+5) / 15 = 2.6
Therefore, the main number of home runs hit per game is 2.6.
How to find the median?b) To find the median, we need to arrange the data set in order from smallest to largest:
0, 1, 1, 2, 2, 2, 3, 3, 4, 4, 5, 5
Since there are an odd number of data points, the median is the middle value, which is 3.
Therefore, the median number of home runs hit per game is 3.
How to find the mode?c) To find the mode, we need to determine which value appears most frequently in the data set. In this case, 2 and 3 each appear three times, which means that there are two modes: 2 and 3.
Therefore, the mode(s) of the number of home runs hit per game for the Millard Girls' Softball team are 2 and 3.
Learn more about mean and mode
brainly.com/question/6813742
#SPJ11
A bag has 25 beads in it.the probability of picking a white bead is 3/5.how many white beads are in the bag
Answers
2/3 divided by 5 please help me I'm bad at math (it needs to be a fraction)
Answers
Answer:
The answer is 4
Step-by-step explanation: I did the work and it works out like that I hope this helps
Suppose that n balls are tossed into n bins, where each toss is independent and the ball is equally likely to end up in any bin. What is the expected number of empty bins
Answers
The expected number of empty bins when tossing n balls into n bins, with each toss being independent and equally likely, can be determined using the concept of probability.
Let's define the probability that a specific bin remains empty after n tosses as P(empty). Since each ball has n choices, there are n^n possible ways to distribute the balls. To find the probability that a specific bin is empty, we can consider the situation where balls can be tossed into the remaining n-1 bins, resulting in (n-1)^n possible distributions. Therefore, P(empty) = ((n-1)^n) / (n^n).
Now, to calculate the expected number of empty bins, we can use the concept of linearity of expectation. The expected value of the sum of random variables is equal to the sum of the expected values of the individual random variables. In this case, the random variables represent the empty status of each bin (1 if empty, 0 if not).
The expected number of empty bins is the sum of the probabilities of each bin being empty, which is n * P(empty). So, the expected number of empty bins = n * (((n-1)^n) / (n^n)).
Using this formula, you can determine the expected number of empty bins when n balls are tossed into n bins independently and with equal likelihood.
Learn more about independent here:
https://brainly.com/question/15375461
#SPJ11
Which function has an inverse that is also a function
Answers
In order for a function to have an inverse that is also a function there are 2 main requirements:
1. The function should be bijective (ie) the function should be one-one ( each element in codomain has not more than 1 pre image in domain) and onto ( Range should be equal to codomain)
2. The inverse function should be defined by a suitable domain and range
Hope this answer helps you..
Described how to use the area to find the quotient 2/3 ÷ 1/5. Check your work by also finding the quotient 2/3÷ 1/5 using numerical operation only.
Answers
Answer: = 2/15
Step-by-step explanation:
Select the product that shows the correct placement of the decimal point
30.76
x 0.08
0 2.4608
0 24.608
X 246.08
2460.8
Answers
Answer:
0 2.4608
Step-by-step explanation:
Answer:
A
Step-by-step explanation:
hope this helps
trust me
Obtain the equation for the least-squares regression line for this data. What is the average chance of admission for a student who scores a 305 on the GRE?
a) 45% (or 0.45)
b) 51% (or 0.51)
c) 61% (or 0.61)
d) 70% (or 0.71)
Answers
The equation for the least-squares regression line for the given data and the average chance of admission for a student who scores a 305 on the GRE are options b) 51% (or 0.51).
To find the equation for the least-squares regression line, we need to first calculate the slope and y-intercept. Let x be the predictor variable (GRE score) and y be the response variable (admission chance). Then, we have:
n = 10 (number of data points)
Σx = 3100
Σy = 52.1
Σxy = 161750
Σx^2 = 96100
Σy^2 = 24.71
The slope, b, can be calculated as:
b = (nΣxy - ΣxΣy) / (nΣx^2 - Σx^2)
= (10(161750) - (3100)(52.1)) / (10(96100) - 3100^2)
= 0.0644
The y-intercept, a, can be calculated as:
a = (Σy - bΣx) / n
= (52.1 - (0.0644)(3100)) / 10
= 0.336
Therefore, the equation for the least-squares regression line is:
y = 0.0644x + 0.336
To find the average chance of admission for a student who scores a 305 on the GRE, we simply substitute x = 305 into the equation and solve for y:
y = 0.0644(305) + 0.336
= 0.5136
So the average chance of admission for a student who scores a 305 on the GRE is b) 51% (or 0.51).
For more questions like Regression click the link below:
https://brainly.com/question/28178214
#SPJ11
Factor the polynomial completely.
3y3 + y2 + 9y + 3
A. y2(3y + 1) + 3(3y + 1)
B. (y + 3)(y + 1)(3y + 1)
C. (y2 + 3)(3y + 1)
D. will not factor
Answers
The completely factorised form of the given polynomial as required to be determined is; Choice C; (y² + 3) (3y + 1).
What is the completely factorised form of the polynomial?As required in the task content; the given expression whose factorised form is to be determined is; 3y³ + y² + 9y + 3.
The completely factorised form can be determined as follows;
y² (3y + 1) + 3 (3y + 1).
Therefore, we have that;
(y² + 3) (3y + 1)
Ultimately, the completely factorised form of the given expression is; Choice C; (y² + 3) (3y + 1).
Read more on factorisation;
https://brainly.com/question/25829061
#SPJ1
the measurement of the edge of a cube is found to be 15 inches, with a possible error of 0.03 inch. (a) use differentials to approximate the possible propagated error in computing the volume of the cube. (b) use differentials to approximate the possible propagated error in computing the surface area of the cube.
Answers
The approximated possible propagated error in computing the volume of the cube is 20.25 .
The approximated possible propagated error in computing the surface area of the cube is 5.4.
The formula's for volume and surface area of cube is as follows,
\(V=a^3\\S=6a^2\)
Where a is the side of the cube.
When you utilize those questionable measurements to calculate something else, error propagation (or uncertainty propagation) occurs to measurement mistakes.
The error in the edge of the cube is 0.03 inch, so
\(a=15\pm0.03\)
Δa=0.03 inches
Now, differentiating the volume function of cube,
\(\frac{dV}{da} =3a^2\\dV=3a^2da\)
Putting the values,
Δ\(dV=3(15)^2\times0.03\\dV=20.25\)
Now, differentiating the surface area function of cube,
\(\frac{dS}{da}=12a\)
Putting the values,
\(dS=12\times15\times da\\dS=12\times15\times 0.03\\dS=5.4\)
Therefore, The approximated possible propagated error in computing the volume of the cube is 20.25 and The approximated possible propagated error in computing the surface area of the cube is 5.4.
To learn more about the propagated error visit here:
https://brainly.com/question/13120993
#SPJ4
how to find the marked price of an article
Answers
Answer:
I don't really know what you mean so I would say to just look on the tag but if you gave more info then I could help you out
Find the lateral surface area of the figure.
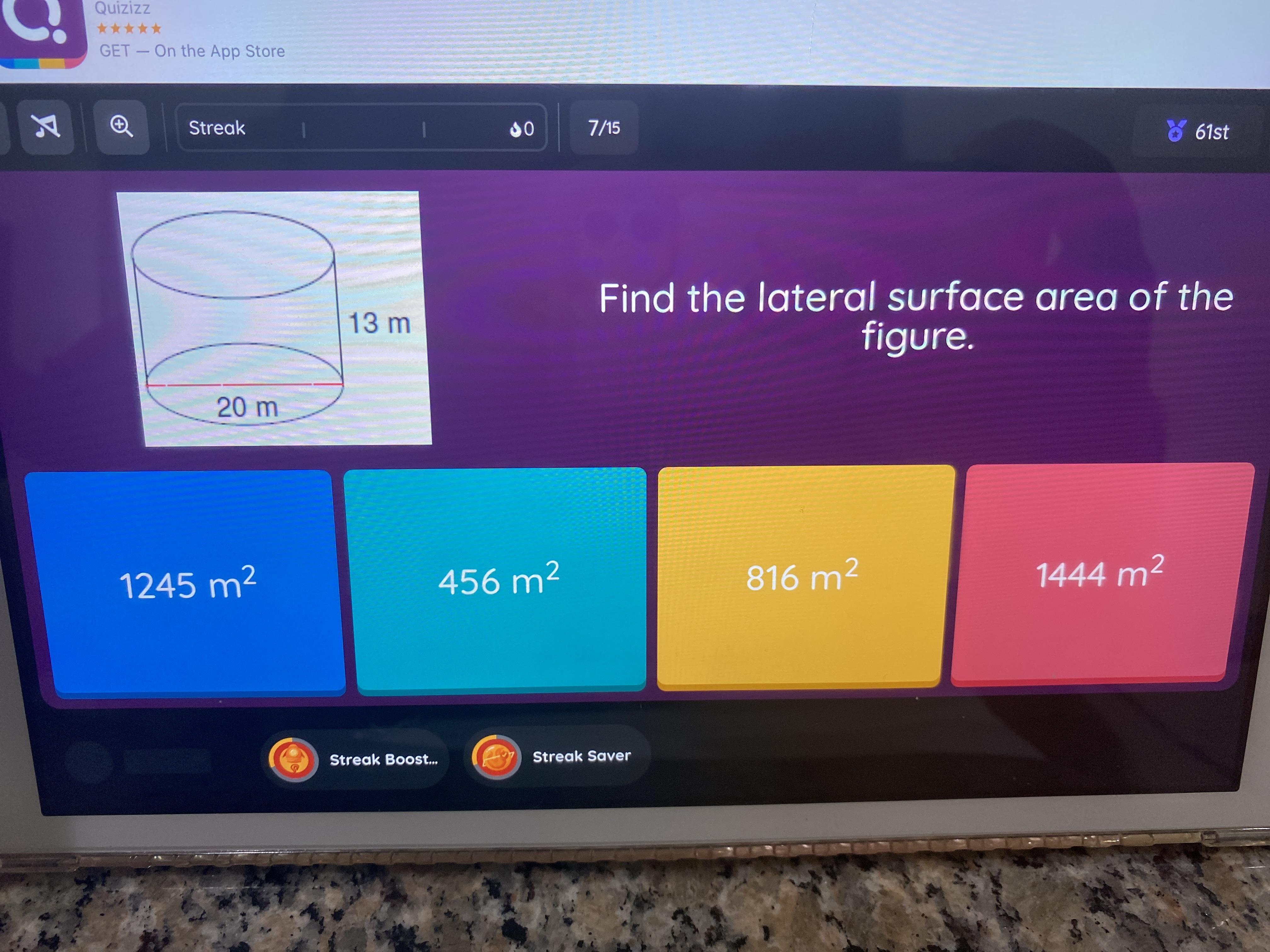
Answers
The evaluated lateral surface area is 261.8 square meters, under the condition that the base length is 20 m and height is 13 m.
The lateral surface area of a cylinder is given by the formula 2πrh
Here,
r = radius of the base
h = height of the cylinder.
For the given case, the base length is 20 m and height is 13 m. Then the base length is stated instead of the radius, we have to evaluate the radius first.
The radius of a cylinder can be found applying the formula r = l/2π
Here,
l = base length.
So, staging l = 20 m
, we get
r = 20/(2π)
≈ 3.18 m
Now that we have received the radius and height, we can evaluate the lateral surface area applying the formula mentioned above.
Staging
r = 3.18 m
h = 13 m,
we get:
Lateral surface area
= 2πrh
≈ 261.8 m²
Then, the lateral surface area of the given cylinder is approximately 261.8 square meters.
To learn more about surface area
https://brainly.com/question/951562
#SPJ1
Solve the equations.
\(\sqrt{x^{2} } =14\)
\(\sqrt{x^{2} } =17\)
\(\sqrt{y^{2} } =5\)
Answers
Answer:
\(x=\pm14\\x=\pm17\\y=\pm5\)
Step-by-step explanation:
Generally, equations in the form \(\sqrt{x^2}=c\) where \(c\) is some constant, would have \(x=\pm c\) as its solution.
This is because the square of a number is always positive regardless of the sign of \(x\).
BRAINLIEST GURANTEED

Answers
Given:
The function is
\(h=3+25t-5t^2\)
To find:
The values of t where h is 8 meters.
Solution:
We have,
\(h=3+25t-5t^2\)
Putting h=8, we get
\(8=3+25t-5t^2\)
\(0=3+25t-5t^2-8\)
\(0=-5+25t-5t^2\)
\(0=-5(1-5t+t^2)\)
Dividing both sides by -5 and interchanging the sides, we get
\(1-5t+t^2=0\)
\(t^2-5t+1=0\)
Here, \(a=1,b=-5,c=1\).
Using quadratic formula, we get
\(t=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}\)
\(t=\dfrac{-(-5)\pm \sqrt{(-5)^2-4(1)(1)}}{2(1)}\)
\(t=\dfrac{5\pm \sqrt{25-4}}{2}\)
\(t=\dfrac{5\pm \sqrt{21}}{2}\)
It can be written as
\(t=\dfrac{5-\sqrt{21}}{2}\) and \(t=\dfrac{5+\sqrt{21}}{2}\)
\(t=0.20871215\) and \(t=4.7912878\)
\(t\approx 0.21\) and \(t\approx 4.79\)
Therefore, the required values of t are 0.21 and 4.79.
You buy a baseball card that goes up in value each year at 12%. You original bought the card for $25. How much will it be worth in 10 years?
Answers
Answer:12 to 25 yrs
Step-by-step explanation:
convert 12% to a decimal
1- In Euclidean space, the locus of points equidistant from the origin of a plane is a circle What is the locus of points equidistant (in the spacetime distance seme) from the origin of a spacetime plane? 151 2. A ruler of length L. In at rest in with its left and at the origin. O moves from left to right with speed relative to o along the length of the ruler. The two origins coincide ut time zero for both, at which time a photon is emitted toward the other end of the rulut. What are the coordinates in Olof the event at which the photon maches the other end? (10) 3. The Earth and Alpha Centauri are 43 light years apart. Ignore their relative motion Events A and B occur att on Earth and at 1 year on Alpha Centauri, respectively. (a) What is the time difference between the events according to an observer moving at B - 0.98 from Earth to Alpha Centauri? (b) What is the time difference between the events according to an observer moving at 3 = 0.98 from Alpha Centauri to Earth? (c) What is the speed of a spacecraft that makes the trip from Alpha Centauri to Earth in 2.5 years according to the spacecraft clocks? (d) What is the trip time in the Earth rest frame? [5+5+5+51 + Plane polar coordinates are related to cartesian coordinates by x=rcos and y = rsin. Describe the transformation matrix that maps cartesian coordinates to polar coordinates, and write down the polar coordinate basis vectors in terms of the basis vectors of cartesian coordinates. [51 5- suppose that we are given a basis ei, es consisting of a pair of vectors making a 45° angle with one another, such that ei hus length 2 and ez has length 1. Find the dual basis vectors for the case of covariant components of the vectors. [101
Answers
1. In the context of spacetime, the locus of points equidistant from the origin of a spacetime plane is a hyperbola.
In Euclidean space, the distance between two points is given by the Pythagorean theorem, which only considers spatial dimensions. However, in spacetime, the concept of distance is extended to include both spatial and temporal components. The spacetime distance, also known as the interval, is given by the Minkowski metric:
ds^2 = -c^2*dt^2 + dx^2 + dy^2 + dz^2,
where c is the speed of light, dt represents the temporal component, and dx, dy, dz represent the spatial components.
To determine the locus of points equidistant from the origin, we need to find the set of points where the spacetime interval from the origin is constant. Setting ds^2 equal to a constant value, say k^2, we have:
-c^2*dt^2 + dx^2 + dy^2 + dz^2 = k^2.
If we focus on a spacetime plane where dy = dz = 0, the equation simplifies to:
-c^2*dt^2 + dx^2 = k^2.
This equation represents a hyperbola in the spacetime plane. It differs from a circle in Euclidean space due to the presence of the negative sign in front of the temporal component, which introduces a difference in the geometry.
Therefore, the locus of points equidistant from the origin in a spacetime plane is a hyperbola.
(Note: The explanation provided assumes a flat spacetime geometry described by the Minkowski metric. In the case of a curved spacetime, such as that described by general relativity, the shape of the locus of equidistant points would be more complex and depend on the specific curvature of spacetime.)
To know more about equidistant, refer here:
https://brainly.com/question/29886221#
#SPJ11
How long does it take for $150 to grow to $450 at 7% annual percentage rate compounded continuously?
Answers
It takes 15.69 years for $150 to grow to $450 at 7% annual percentage rate compounded continuously
what is compound interest?
Interest that is added to a loan or deposit sum is known as compound interest. In our daily lives, it is the notion that is employed the most frequently. Compound interest is calculated for a sum using the principal and interest accrued over time. Compound interest and simple interest differ primarily in this way.
Initial amount = P = $150
Final amount = A= $450
rate , r= 7% = 0.07
t = ?
Formula:
A=Pe^(rt)
450=150(2.7183)^(0.07*t)
(2.7183)^(0.07*t) = 450/150 = 3
Taking Ln on both sides, we get
(0.07*t) Ln(2.7183) = Ln(3)
=> t= Ln(3) /[ 0.07Ln(2.7183) ] = 15.69 years
It takes 15.69 years for $150 to grow to $450 at 7% annual percentage rate compounded continuously
To learn more about compound interest from the link
https://brainly.com/question/24274034
#SPJ1