Answers
Answer:
1
Step-by-step explanation:
two zeros. If we change C from -1 to plus 1, the parabola is completely above the X-axis, so it has no zeros. If we change the value of A from positive 1 to -1, the parabola will open downward, and it will have . The B value can also change the number of zeros.
Answer:
2
Step-by-step explanation:
The zeros are the number of times that the graph crosses the x axis
This parabola crosses the x axis 2 times so it has two zeros
Related Questions
Is it Linear, exponential, quadratic or neither

Answers
Answer:
exponential
Step-by-step explanation:
put it on a graphing calculator and you'll see
The line y = 5x + 2 is shown. -22- 20 18 16 14 12 10- 8 6 0 6 8 Eva wants to use the line to solve the equation 5x + 2 = 11 a) Explain how Eva could do this.
Answers
She will plot a graph using the given points and trace the point y = 11 to the x-axis.
What is a linear equation?A linear equation is an equation in which the highest power of the variable is always 1. It is also known as a one-degree equation. The standard form of a linear equation in one variable is of the form Ax + B = 0. Here, x is a variable, A is a coefficient and B is constant.
Firstly she would have form tables of values for x and y using y = 5x + 2 x-values had been given as -22- 20 18 16 14 12 10- 8 6 0 6 8 .
Then plot a graph of the line y =5x + 2 with y on the vertical and x on the horizontal.
After plotting the graph, on the vertical axis trace y = 11, draw a horizontal line from y = 11 until it just touches the straight line graph from that point drop a vertical line until it touches the x-axis. the value of x there is the solution of the equation y = 5x +2.
Learn more about Linear graphs: htps://brainly.com/question/14323743
#SPJ1
3. Why do communities need healthy citizens?
Citizens who are healthy watch T.V. a lot and buy what they see in commercials.
O Citizens who are healthy contribute more to their communities.
Citizens who are healthy create more problems for their communities.
Citizens who are healthy move from place to place.
Answers
Answer:
B
Step-by-step explanation:
O Citizens who are healthy contribute more to their communities.
( I don't think this is math related).
Encontrar la magnitud de la velocidad angular de un disco de 0.75 rev/así como la magnitud de su desplazamiento angular Si su movimiento duró 180 segundos
Answers
Answer:
La magnitud de la velocidad angular es 0.026 rad/s y la magnitud del desplazamiento angular es 4.71 rad.
Step-by-step explanation:
Podemos encontrar la magnitud de la velocidad angular (ω) del disco con la siguiente ecuación:
\( \omega = \frac{\theta}{t} \)
En donde:
θ: es el desplazamiento angular = 0.75 rev
t: es el tiempo = 180 s
Primero debemos cambiar las unidades del desplazamiento angular de revoluciones a radianes:
\( \theta = 0.75 rev*\frac{2\pi rad}{1 rev} = 4.71 rad \)
Entonces, la velocidad angular es:
\( \omega = \frac{4.71 rad}{180 s} = 0.026 rad/s \)
Por lo tanto, la magnitud de la velocidad angular es 0.026 rad/s y la magnitud del desplazamiento angular es 4.71 rad.
Espero que te sea de utilidad!
PLEASE help me understand the steps to solve this i feel like crying i dont understand

Answers
Answer:
4
Step-by-step explanation:
First:
(-2 1/2)*(-1 3/5) = 2.5*1.6
Second:
2.5*1.6=5/2*8/5
Third:
5/2*8/5=
4
The mass of a red blood cell is about 2.7 X 10−112.7 X 10 −11 grams. There are about 2.5 X 10132.5 X 10 13 red blood cell in a human body. What is the total mass, in grams, of the red blood cells in a human body? Express your answer in standard form
Answers
Answer:
6.75 x 10^2 g
Step-by-step explanation:
Mass of Red Blood Cells
The mass of a red blood cell is about 2.7 X 10−112.7 X 10 −11 grams. There are about 2.5 X 10132.5 X 10 13 red blood cell in a human body. What is the total mass, in grams, of the red blood cells in a human body? Express your answer in standard form
To find the total mass of red blood cells in a human body, we need to multiply the mass of one red blood cell by the total number of red blood cells in the body:
Total mass = (mass of one red blood cell) x (total number of red blood cells)
Total mass = (2.7 x 10^-11 grams) x (2.5 x 10^13 red blood cells)
Multiplying these two numbers gives:
Total mass = 6.75 x 10^2 grams
In standard form, this is:
Total mass = 6.75 x 10^2 g
Find r, T, N, and B at the given value of t. Then find the equations for the osculating, normal, and rectifying planes at that value of t. r(t) = (cos t)i + (sin t)j - 5k, t = pi/2 r(pi/2) = (0)i + (1)j + (-5)k (Type exact answer, using radicals as needed.) T(pi/2) = (-1)i + (0)j + (0) k (Type exact answer, using radicals as needed.) N(pi/2) = (0)i + (-)j + (0)k (Type exact answer, using radicals as needed.) B(pi/2) = (0)i + (0)j + (1)k (Type exact answer, using radicals as needed.) Choose the correct equation for the osculating plane at t = pi/2. -y = -1 -x = 0 z = -5 Squareroot 3/2 x + 1/2 y = 5
Answers
the equations for the osculating, normal, and rectifying planes at t = pi/2 are:
Osculating plane: z = -j * (t - pi/2) - 5
Normal plane: y = -i * (t - pi/2) + 1
Rectifying plane: x = 1.
To find the values of r, T, N, and B at t = pi/2, we first need to calculate r(pi/2) and its derivatives.
r(t) = (cos t)i + (sin t)j - 5k
r(pi/2) = (cos(pi/2))i + (sin(pi/2))j - 5k
= 0i + 1j - 5k
= <0, 1, -5>
To find T(pi/2), we need to take the derivative of r(t) and evaluate it at t = pi/2.
r'(t) = (-sin t)i + (cos t)j + 0k
r'(pi/2) = (-sin(pi/2))i + (cos(pi/2))j + 0k
= -i
Since T(pi/2) is the unit tangent vector at t = pi/2, we need to normalize r'(pi/2) to get T(pi/2).
|T(pi/2)| = |r'(pi/2)| = |-i| = 1
T(pi/2) = r'(pi/2) / |r'(pi/2)|
= (-i) / 1
= -i
= <-1, 0, 0>
To find N(pi/2), we need to take the second derivative of r(t) and evaluate it at t = pi/2.
r''(t) = (-cos t)i - (sin t)j + 0k
r''(pi/2) = (-cos(pi/2))i - (sin(pi/2))j + 0k
= 0i - 1j + 0k
= <0, -1, 0>
Since N(pi/2) is the unit normal vector at t = pi/2, we need to normalize r''(pi/2) to get N(pi/2).
|N(pi/2)| = |r''(pi/2)| = |<0, -1, 0>| = 1
N(pi/2) = r''(pi/2) / |r''(pi/2)|
= <0, -1, 0> / 1
= <0, -1, 0>
To find B(pi/2), we can use the formula B = T x N, where x denotes the cross product.
B(pi/2) = T(pi/2) x N(pi/2)
= <-1, 0, 0> x <0, -1, 0>
= <0*0 - (-1)*0, 0*0 - 0*0, (-1)*(-1) - 0*0>
= <0, 0, 1>
Therefore, we have:
r(pi/2) = <0, 1, -5>
T(pi/2) = <-1, 0, 0>
N(pi/2) = <0, -1, 0>
B(pi/2) = <0, 0, 1>
To find the equations of the osculating, normal, and rectifying planes at t = pi/2, we can use the following formulas:
Osculating plane: r(pi/2) + [r'(pi/2) x r''(pi/2)] / |r'(pi/2)|^2 * (t - pi/2)
Normal plane: r(pi/2) + [r''(pi/2) x [r'(pi/2) x r''(pi/2)]] / |r''(pi/2)|^2 * (t - pi/2)
Rectifying plane: r(pi/2) x [r'(pi/2) x r''(pi/2)] / |r'(pi/2)|^2
Plugging in the values we found earlier, we get:
Osculating plane: (0)i + (1)j + (-5)k + [(-i) x <0, -1, 0>] / |-i|^2 * (t - pi/2)
= (0)i + (1)j + (-5)k - j * (t - pi/2)
Normal plane: (0)i + (1)j + (-5)k + [<0, -1, 0> x [-i x <0, -1, 0>]] / |<0, -1, 0>|^2 * (t - pi/2)
= (0)i + (1)j + (-5)k + (-i*(t - pi/2)
Rectifying plane: <0, 1, -5> x [-i x <0, -1, 0>] / |-i|^2
= <0, 1, -5> x <0, 0, -1>
= <1, 0, 0>
Therefore, the equations for the osculating, normal, and rectifying planes at t = pi/2 are:
Osculating plane: z = -j * (t - pi/2) - 5
Normal plane: y = -i * (t - pi/2) + 1
Rectifying plane: x = 1.
Note that these equations are in the form of a plane equation ax + by + cz = d, where a, b, c are the components of the normal vector to the plane, and d is the distance from the origin to the plane.
Visit to know more about Osculating plane:-
https://brainly.com/question/30781925
#SPJ11
6 the standard deviation of human body temperatures is equal to 0. 62 F. Identify the null hypothesis and alternative hypothesis in symbolic form
Answers
The null hypothesis exists that the standard deviation σ exists equivalent to 0.62. The alternative hypothesis exists that it does not equivalent 0.62.
What are null and alternative hypotheses?Statistical hypothesis testing employs null and alternate hypotheses. While the alternative hypothesis states your research's prediction of an effect or relationship, the null hypothesis of a test always predicts no effect or no association between variables.
A proposed claim or defense in the hypothesis test is referred to as an alternative hypothesis in statistics. In most cases, it supports the research premise and shows that there is a statistical relationship between the variables. It is one of the two statements in statistical hypothesis testing that are mutually exclusive.
H₀: σ = 0.62
H₁: σ ≠ 0.62
The null hypothesis exists that the standard deviation σ exists equivalent to 0.62.
The alternative hypothesis exists that it does not equivalent 0.62.
To learn more about null and alternative hypothesis refer to:
https://brainly.com/question/25263462
#SPJ4
Type the correct answer in each box.
What values of a and b make this equation true?
(4 + ✓–49) – 2(/(-4)2 + V–324) = a + bi
Answers
Answer:
-4 , -29
Step-by-step explanation:
The values of a and b that make the equation true are -28 and -9, respectively
How to determine the true values of a and b?The equation is given as:
(4 + √-49) – 2((-4)² + √–324) = a + bi
Evaluate the exponents
(4 + 7i) – 2(16 + 18i) = a + bi
Expand the bracket
4 + 7i – 32 - 16i = a + bi
Collect like terms
4 – 32 + 7i - 16i = a + bi
Evaluate like terms
-28 -9i = a + bi
By comparison, we have:
a = -28 and b = -9
Hence, the values of a and b that make the equation true are -28 and -9, respectively
Read more about complex numbers at:
https://brainly.com/question/10662770
#SPJ2
i am equivalent to 5/6 . the sum of my numerator and my denominator is 44. the sum of the digits in my denominator is 6. what fraction am i?
Answers
The fraction that satisfies the problem is 20/24.
Equivalent fractions are fractions that have the same value, but different numerators and denominators.
If the fraction is equivalent to 5/6, then the numerator and denominator of the fraction is a multiple of 5 and 6, respectively.
Let x be the factor
fraction = 5x / 6x
If the sum of my numerator and my denominator is 44, then:
5x + 6x = 44
11x = 44
x = 4
fraction = 5x / 6x = 20/24
The final statement says that the sum of the digits in the denominator is 6.
2 + 4 = 6
Hence, the fraction is 20/24.
Learn more about Equivalent fractions here: https://brainly.com/question/18456272
#SPJ4
Given the function f(x)= 23-2x, if f(x) =9, find x
Answers
Answer: 7
Step-by-step explanation:
If f(x) = 9, we can substitute it in the function and solve for x:
f(x) = 23 - 2x = 9
Subtracting 23 from both sides, we get:
-2x = 9 - 23 = -14
Dividing both sides by -2, we get:
x = -14/-2 = 7
Therefore, the value of x when f(x) = 9 is 7.
Chamoy drove 585 miles in 9 hours. Freddy drove 605 miles in 11 hours. Who drove at a faster rate?
Answers
Answer:
Chamoy
Step-by-step explanation:
585/9= 65
605/11= 55
Please help NEEDED ASAP!!!!
taxi cab tariffs in London, England, are as follows.
For the first 234.8 metres or 50.4 seconds (whichever is reached first)
there is a minimum charge of 2.60 GBP.
For each additional 117.4 metres or 25.2 seconds (whichever is reached first), if the distance travelled is less than 9656.1 metres there is a charge of 0.20 GBP.
Once the distance has reached 9656.1 metres then there is a charge of 0.20 GBP for each additional 86.9 metres or 18.7 seconds (whichever is reached first)
1. Develop a piecewise linear model for the cost, C, of a taxi ride based on the distance travelled, m, in metres.
2. Find the cost of 0.2 km, 5 km, and 15 km rides.
3. Develop a piecewise linear model for the cost, D, of a taxi ride based on the time taken, t, in seconds, ignoring distance.
4. Find the cost of 0.5 minute, 5 minute, and 15 minute rides.
5. Given that the actual taxi fare is always the greater of the two models, find:
(i) the cost of a ride that takes 10 minutes to go 4 km (if) the cost of a ride that takes 5 minutes to go 4 km
Answers
Answer:
1. A piecewise linear model for the cost, C, of a taxi ride based on the distance travelled, m, in meters can be represented as:
C = 2.60 (m<234.8)
C = 2.60 + 0.20(m-234.8) (234.8<=m<9656.1)
C = 2.60 + 0.20(9656.1-234.8) + 0.20(m-9656.1) (m>=9656.1)
2.To find the cost of 0.2 km, 5 km, and 15 km rides:
0.2 km = 200 m, the cost would be 2.60 GBP
5 km = 5000 m, the cost would be 2.60 + (0.20 * (5000-234.8)) GBP = 2.60 + 858 GBP = 1118 GBP
15 km = 15,000 m, the cost would be 2.60 + (0.20 * (9656.1-234.8)) + 0.20(15,000-9656.1) GBP = 2.60 + (0.20 * 9656.1-234.8) + 0.20(15,000-9656.1) = 2.60 + 1712.2 + 2040 = 3964.8 GBP
3. A piecewise linear model for the cost, D, of a taxi ride based on the time taken, t, in seconds, ignoring distance can be represented as:
D = 2.60 (t<50.4)
D = 2.60 + 0.20(t-50.4) (50.4<=t<1260)
D = 2.60 + 0.20(1260-50.4) + 0.20(t-1260) (t>=1260)
4. To find the cost of 0.5 minute, 5 minute, and 15 minute rides:
0.5 minute = 30 seconds, the cost would be 2.60 GBP
5 minutes = 300 seconds, the cost would be 2.60 + (0.20 * (300-50.4)) GBP = 2.60 + 44 GBP = 2.60+44 = 3.04 GBP
15 minutes = 900 seconds, the cost would be 2.60 + (0.20 * (1260-50.4)) + 0.20(900-1260) GBP = 2.60 + (0.20 * 1260-50.4) + 0.20(900-1260) = 2.60 + 252 + -12 GBP = 2.48 GBP
5. Given that the actual taxi fare is always the greater of the two models, find:
(i) the cost of a ride that takes 10 minutes to go 4 km is 1118 GBP (by distance model)
(ii) the cost of a ride that takes 5 minutes to go 4 km is 3.04 GBP (by time model)
It is important to
Helpppp help helppppppp

Answers
Answer:
56 degrees
Step-by-step explanation:
Answer:
They are a linear pair so m<B is 56 degrees
Step-by-step explanation:
In order to make a profit, a retailer will mark up the cost of an item. If the cost of the item is $42 but it is sold for
$89, what is the mark up rate for the item?
Round your answer to the whole percent.
Answers
you may not use the break and continue statements within the same set of nested loops. t/f
Answers
The given statement is false because In programming, the break and continue statements serve different purposes and can be used independently or together within nested loops.
The break statement is used to exit the current loop prematurely. When encountered, it terminates the loop and continues with the next statement after the loop. This can be useful when a specific condition is met, and you want to stop the execution of the loop immediately.
The continue statement, on the other hand, is used to skip the current iteration of a loop and move on to the next iteration. It allows you to skip certain iterations based on a specific condition without terminating the entire loop.
Both break and continue statements can be used within nested loops. In such cases, the break statement will exit only the innermost loop it is placed in, while the continue statement will skip to the next iteration of the innermost loop.
By using break and continue strategically within nested loops, you can control the flow of execution based on specific conditions. This flexibility allows you to fine-tune the behavior of your program and optimize its efficiency.
For more such questions on programming visit:
https://brainly.com/question/23275071
#SPJ11
Note : This is a computer science question
Please, can someone help me with this math? I would greatly appreciate it!
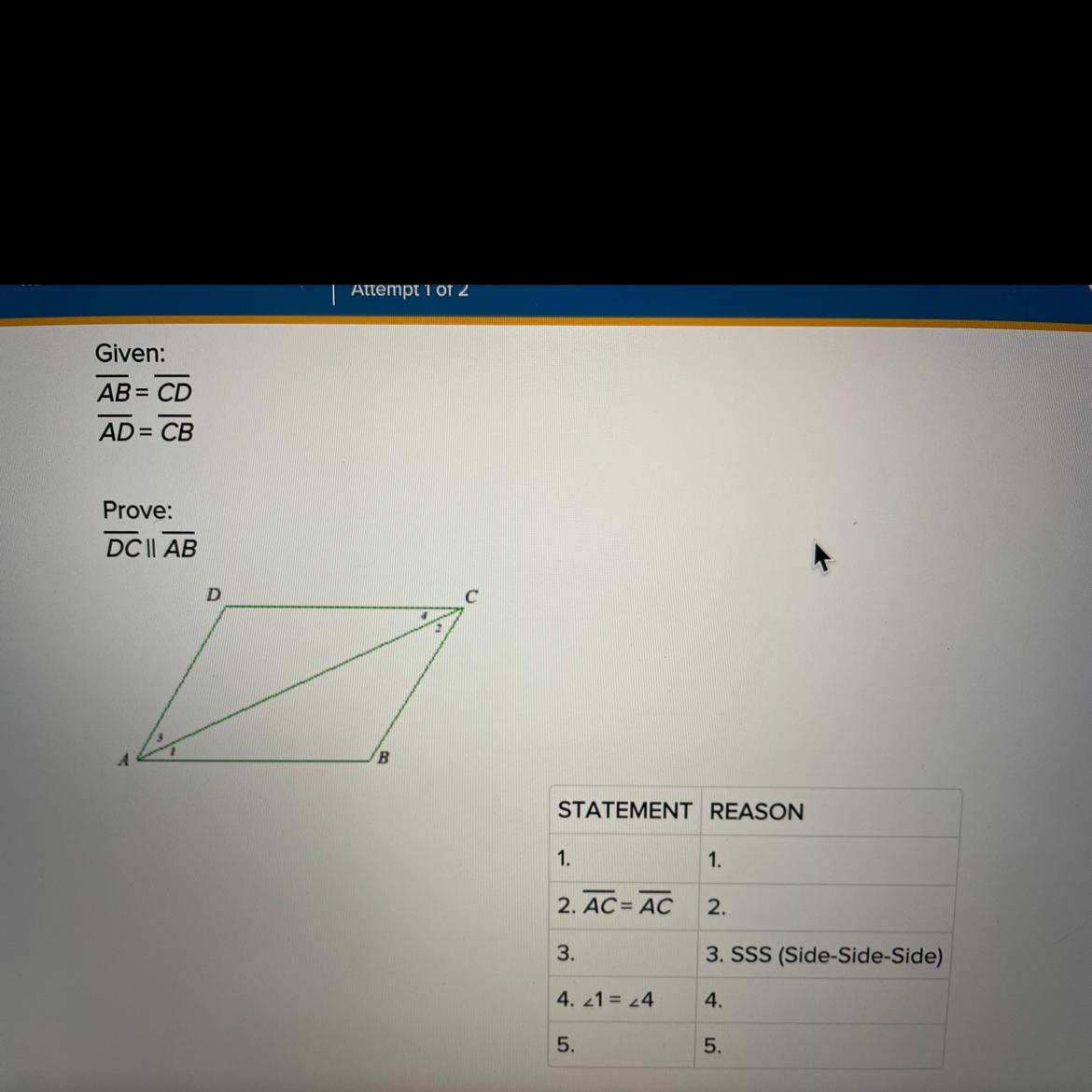
Answers
The proof that shows that lines DC and AB are parallel is shown below.
What is the SSS Congruence Theorem?The SSS congruence theorem states that two triangles that have three corresponding congruent sides are congruent to each other.
When two triangles are proven to be congruent triangles, invariably, we can state that the corresponding parts of both triangles are also equal to each other by CPCTC.
The following proof shows lines DC and AB are parallel lines:
Statement Reasons
1. AB = CD 1. Given
AD = CB
2. Line AC = Line AC 2. Reflexive property
3. Triangle ADC ≅ Triangle ABC 3. SSS
4. Angle 1 ≅ Angle 4 4. CPCTC
5. DC║AB 5. Converse of alternate interior ∠s theorem
Learn more about the SSS theorem on:
https://brainly.com/question/2102943
#SPJ1
A boat is 122 meters from the base of a lighthouse. The lighthouse is 34 meters tall. The angle formed with the lighthouse and sea level is 90 degrees. A boat is 122 meters from the base of a lighthouse that is 34 meters above sea level. What is the angle of elevation from the boat to the top of the lighthouse? Round to the nearest degree. °.
Answers
The angle is 29.1234 degree
Height and distanceIt is an application of trigonometric by which we can find the height, distance, and angle.
Given(x) = 122 m
Height of lighthouse (h) = 34
The base of a lighthouse that is 34 meters above sea level (l) = 34
To findThe angle of elevation from the boat to the top of the lighthouse.
Step by step explanationTotal height of the tower from the sea level = 34 + 34
Total height of the tower from the sea level = 68
Then
\(\begin{aligned} tan \theta &= \dfrac{Total height of tower from the sea level}{Distance between boat and light and lighthouse} \\tan \theta &= \dfrac{68}{122} \\\theta &= tan^{-1} (\dfrac{68}{122} )\\\theta &= 29.132429^{o} \\\end{aligned}\)
Thus, the angle is 29.1234 degree
More about the Height and distance link is given below.
https://brainly.com/question/10681300
16 is the answer edge 2022
A rectangle has a perimeter, P, length, l, and width, w. Which of the following represents l in terms of P and w?
Answers
Answer: l = P/2 - w
Step-by-step explanation:
Perimeter formula for rectangle :
P = 2( l + w )
We have to write l in terms of P and W.
P/2 = ( l + w)
P/2 - w = l
Now, flip the equation and you'll get :
l = P/2 - w
Can someone please give me the answer for this?

Answers
Answer:
y=(6,3)+(-2,1)
;) theres ur answer bby girlhow many solutions are there to square root x =9
Answers
Answer:
There are 2 solutions to square root x = 9
They are 3, and -3
Step-by-step explanation:
The square root of x=9 has 2 solutions,
The square root means, for a given number, (in our case 9) what number times itself equals the given number,
Or, squaring (i.e multiplying with itself) what number would give the given number,
so, we have to find the solutions to \(\sqrt{9}\)
since we know that,
\((3)(3) = 9\\and,\\(-3)(-3) = 9\)
hence if we square either 3 or -3, we get 9
Hence the solutions are 3, and -3
Write in standard form and in both expanded forms 6x10°-4-10-1+3x10-3+7x10 ++2x10-5
Answers
Answer: 6x10°+97
Step-by-step explanation:
6x10°-4-10-1+30-3+7x10+2x10-5
6x10°-4-10-1+30-3+70+2x10-5
6x10°-4-10-1+30-3+70+20-5
6x10°+97
can someone help me ?

Answers
Answer:
c
Step-by-step explanation:
How are the properties of exponents used when dividing a polynomial by a monomial?
Answers
Answer:
a couple different obes
Step-by-step explanation:
there are five
9. The length of a rectangle is 6 inches more than its width. If the perimeter of the
rectangle is 24 inches, find its dimensions
Answers
Answer:
Width is 3 length is 9 :)
Step-by-step explanation:
I'm doing this stuff right now
Define the functions f,g:R→R as f(x):=e
−x
2
and g(x):=e
−2x
2
. Use the Fourier transform in order to compute the convolution f∗g. You may (and should) use the table in Kreyszig, p. 536, for the computation of the Fourier transform of e
−ax
2
.
Answers
The convolution of f and g is\(f * g(x) = 1 / sqrt(3pi) * e^(-2x^2 / (3pi)).\)
To compute the convolution of two functions f and g using the Fourier transform, we'll follow these steps:
Find the Fourier transforms of f(x) and g(x).
Use the convolution theorem, which states that the Fourier transform of the convolution of two functions is the product of their individual Fourier transforms.
Take the inverse Fourier transform to obtain the convolution.
Let's start by finding the Fourier transforms of f(x) and g(x):
Fourier transform of\(f(x): f(x) = e^(-x^2)\)
According to the table in Kreyszig (p. 536), the Fourier transform of e^(-ax^2) is given by:
\(F{e^(-ax^2)} = sqrt(pi/a) * e^(-pi^2 * xi^2 / a)\)
For f(x) with a = 1:
\(F{f(x)} = sqrt(pi) * e^(-pi^2 * xi^2)\)
Fourier transform of\(g(x): g(x) = e^(-2x^2)\)
For g(x) with a = 2:
\(F{g(x)} = sqrt(pi/2) * e^(-pi^2 * xi^2 / 2)\)
Now, we apply the convolution theorem:
Convolution theorem: If F{f(x)} = F_f(xi) and F{g(x)} = F_g(xi), then the Fourier transform of the convolution f * g is given by F{f * g} = F_f(xi) * F_g(xi).
Therefore, the Fourier transform of the convolution f * g is:
\(F{f * g} = (sqrt(pi) * e^(-pi^2 * xi^2)) * (sqrt(pi/2) * e^(-pi^2 * xi^2 / 2))\)
=\(sqrt(pi^3 / 2) * e^(-3pi^2 * xi^2 / 2)\)
Now, we need to take the inverse Fourier transform to find the convolution result:
Inverse Fourier transform of\(F{f * g} = F_f * F_g = sqrt(pi^3 / 2) * e^(-3pi^2 * xi^2 / 2)\)
According to the table in Kreyszig (p. 536), the inverse Fourier transform of e^(-ax^2) is given by:
\(F^(-1){e^(-ax^2)} = 1 / sqrt(2a) * e^(-x^2 / 4a)\)
Therefore, the convolution of f and g, denoted as f * g, is given by:
\(f * g (x) = F^(-1){F{f * g}}\)
=\(1 / sqrt(2 * (3pi^2 / 2)) * e^(-x^2 / (4 * (3pi^2 / 2)))\)
=\(1 / sqrt(3pi) * e^(-2x^2 / (3pi))\)
So, the convolution of f and g is\(f * g(x) = 1 / sqrt(3pi) * e^(-2x^2 / (3pi)).\)
Learn more about convolution
https://brainly.com/question/32643048
#SPJ11
Complete the fraction that is equivalent to . = ¯¯¯¯¯ 24
Answers
Answer:
24 is equivalent to 24/1
Step-by-step explanation: Hope this helped you feel free to ask questions in comments.
The diameter of a Ferris wheel is 80 feet.
a. If the Ferris wheel makes one revolution every 45 seconds, find the linear velocity of a person riding in the Ferris wheel.
b. Suppose the linear velocity of a person riding in the Ferris wheel is 8 feet/second. What is the time for one revolution of the Ferris wheel?
a. v=5.6 ft/s
b. t=31 seconds
Answers
Linear velocity of a person riding is 5.6 ft/s and time for one revolution of ferries wheel is 31.8 sec.
What is linear velocity?
Linear velocity, v, is defined as the rate of change of linear displacement, s, with respect to time, t.
On a ferries wheel, displacement = circumference of the wheel = 2πr
Hence linear velocity, v = 2πr/T
According to the given question:
Diameter of the wheel is 80 feet
So, radius of wheel = 40 feet
If Ferris wheel makes one revolution is 45 seconds
Then linear velocity
v = 2πr/T = 2 x 3.14 x 40/45
v = 5.6 ft/s
If linear velocity of a person riding on wheel is 8 ft/s then time for one revolution
T = 2πr/v = 2 x 3.14 x 40/ 8
T = 31.8 sec
To know more about linear velocity visit
https://brainly.com/question/16123156
#SPJ4
suppose that 30% of the applicants for a certain industrial job possess advanced training in computer programming. applicants are interviewed sequentially and are selected at random from the pool. find the probability that the first applicant with advanced training in programming is found on the fifth interview.
Answers
The probability of finding the first applicant with advanced training in programming on the fifth interview is approximately 0.072.
To solve this problem, we can use the geometric distribution, which models the probability of a certain event (in this case, finding an applicant with advanced training in programming) occurring for the first time after a certain number of trials (in this case, interviews).
The probability of finding an applicant with advanced training in programming on any given interview is 0.3, since 30% of the applicants possess this qualification. Therefore, the probability of not finding an applicant with advanced training in programming on any given interview is 0.7.
To find the probability that the first applicant with advanced training in programming is found on the fifth interview, we need to calculate the probability of not finding any such applicant on the first four interviews (which is (0.7)^4) and then finding one on the fifth interview (which is 0.3).
Therefore, the probability that the first applicant with advanced training in programming is found on the fifth interview is:
(0.7)^4 * 0.3 = 0.07203 (rounded to five decimal places)
So the answer is that the probability of finding the first applicant with advanced training in programming on the fifth interview is approximately 0.072.
Learn more about probability here
https://brainly.com/question/25839839
#SPJ11
Find the area of the figure. Use 3.14 for π.

Answers
Answer:
146.93 m^2
Step-by-step explanation:
1. Area of the triangle plus the area of the semicircle.
2. Triangle: b x h x .5 14 x 10 x .5= 70
3. area of semicircle: (πr^2).5 7^2 x π x .5 = 76.93
We halved the area of a circle since we have half a circle.
4. 76.93+70= 146.93
