How often does always never sometimes
1. a parallelogram is equilateral.
2. two pairs of consecutive sides of a rhombus are congruent
3. kies have at least one pair of congruent : opposite angles.
Answers
1) sometimes
2) always
3) always
Related Questions
What is the value of the expression below?
-(-4)(-6)-3/5(10+15)
______________
1/3
A) -117
B) -13
C) 3
D) 27
Answers
Answer:
Answer is A
- 117
_______________________________________
Answer:
ay wee tologo bo sharmaine?
show the following equations on a number line. a) -16 < 4x _ x÷2
Answers
Step-by-step explanation:
-16(2)<4x(2)-x/2(2)
-32<8x-x
-32<7x
-32/7<7x/7
-32/7<x
-4.5714285714285714<x
~-4.56<x
So after drawing the number line, indicate it starting from negative 4.6 and pointing the arrow towards the right. Do not shade
Find x and Angle EFG.

Answers
2. What was the volume of each small cube?
1/32
1/64
1/128
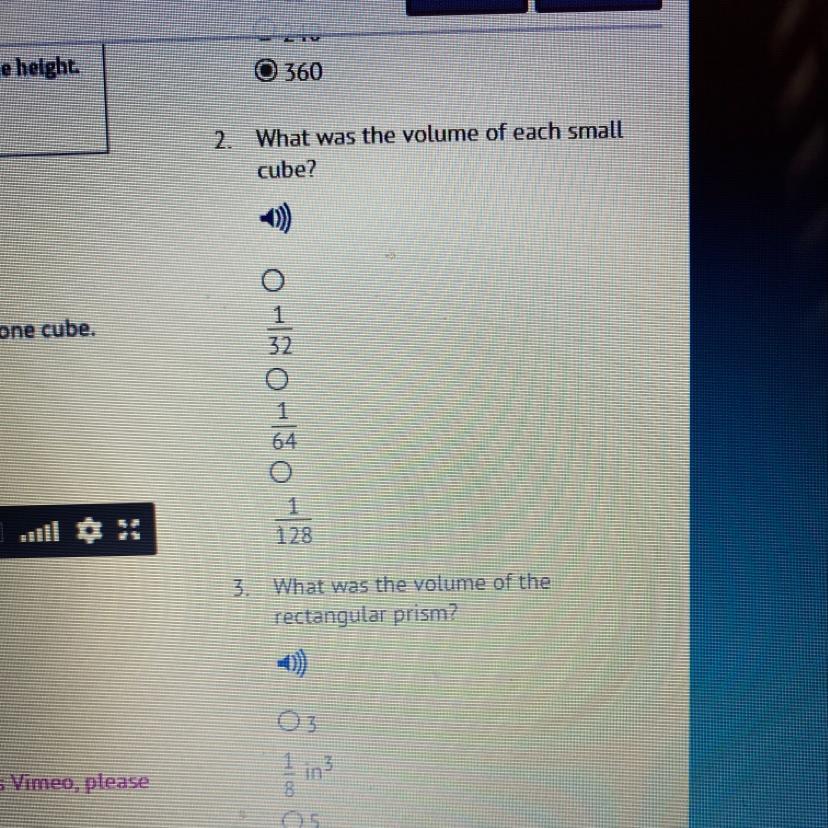
Answers
Answer:
1/64
Step-by-step explanation:
math help pls! i’m not sure how to solve this

Answers
Answer:
-sin(x)
Step-by-step explanation:
im not sure what the 'difference quotient' means, but the derivative of cos(x) is just -sin(x).
A walkway forms one diagonal of a square playground. The walkway is 32m long. How long is a side of the playground
Answers
Answer:14 meters
Step-by-step explanation:
Function A is given by the equation y = 3 x + 10 . Function is given by the example show. When x = 1, y =10. When x = 2, y = 13. When x = 3, y = 16. When x = 4, y = 19.
Function A has a..
A. Greater rate of change
B. Smaller rate of change
C. Greater y-intercept
D. Smaller y- intercept
Answers
Answer: both of you have a lead yet but you can get it right away if I can see you guys again in a developer way but I have a game pass
Step-by-step explanation: yes
Is Brainly a cheating website? Pretty sure it is. Just curious. Let me know so I can figure it out.
Answers
Because students put links that are irrelevant question or answer
If you take it in a positive manner then it’s no
Because many students share their own relevant answers that helps someone to understand something properly
which expression has the same value as -8 + (4)
Answers
Answer:
the answer would be -4 because that's the simplified version of -8+(4)
Sal's Sandwich Shop sells wraps and sandwiches as part of its lunch specials. The profit on every sandwich is $2, and
last month. The equation 2x + 3y = 1,470 represents Sal's profits last month, where x is the number of sandwich lunch
1. Change the equation to slope-intercept form. Identify the slope and y-intercept of the equation. Be sure to show
2. Describe how you would graph this line using the slope-intercept method. Be sure to write using complete sente
3. Write the equation in function notation. Explain what the graph of the function represents. Be sure to use comples
4. Graph the function. On the graph, make sure to label the intercepts. You may graph your equation by hand on a
5. Suppose Sal's total profit on lunch specials for the next month is $1,593. The profit amounts are the same: $2 for
sentences, explain how the graphs of the functions for the two months are similar and how they are different.
02.03 Key Features of Linear Functions-Option 1 Rubric
Requirements
Student changes equation to slope-intercept form. Student shows all work and identifies the slope and y-intercept of the
Student writes a description, which is clear, precise, and correct, of how to graph the line using the slope-intercept meth
Student changes equation to function notation. Student explains clearly what the graph of the equation represents.
Student graphs the equation and labels the intercepts correctly.
Student writes at least three sentences explaining how the graphs of the two equations are the same and how they are different.
Answers
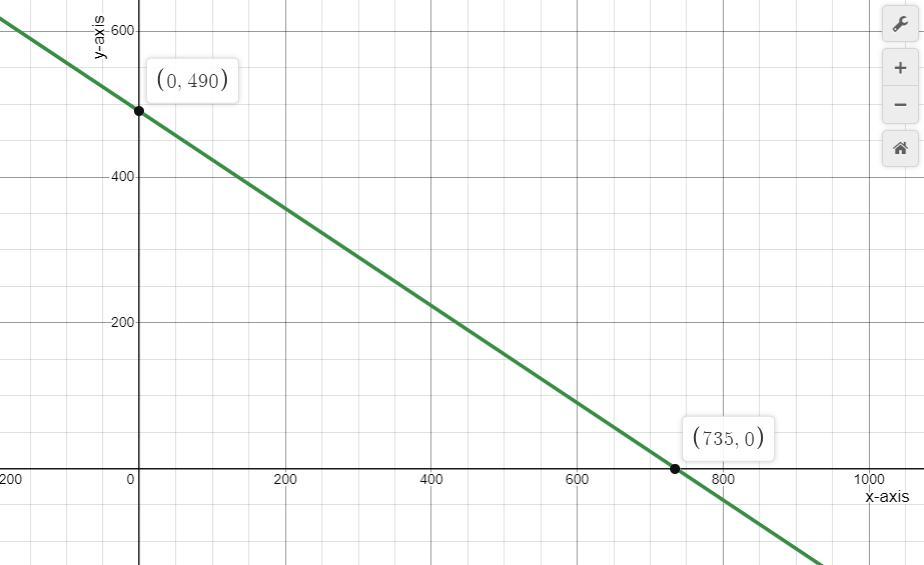
1. The equation to slope-intercept form is y = -2/3(x) + 490. The slope is -2/3 and the y-intercept is 490.
2. You should start at the y-intercept (0, 490) and move right by 3 units and downward by 2 units, and then connect the points.
3. The equation in function notation is f(x) = -2/3(x) + 490. The graph of the function is the rate of change with respect to the number of sandwich lunch sold.
4. A graph of the function with intercepts is shown below.
5. The graphs of the functions for the two months both have the same slope but different y-intercept and x-intercept.
How to change the equation to slope-intercept form?In Mathematics and Geometry, the slope-intercept form of the equation of a straight line is given by this mathematical equation;
y = mx + b
Where:
m represent the slope or rate of change.x and y are the points.b represent the y-intercept or initial value.Based on the information provided above, a linear equation that models Sal's Sandwich Shop's profit is given by;
2x + 3y = 1,470
By subtracting 2x from both sides of the equation and dividing by 3, we have:
2x + 3y - 2x = 1,470 - 2x
y = -2/3(x) + 490
Therefore, the slope is -2/3 and the y-intercept is 490.
Part 2.
In order to graph the equation by using the slope-intercept method, you would start at the y-intercept (0, 490) and move right by 3 units and down by 2 units, and then connect the points.
Part 3.
Next, we would write the equation in function notation as follows;
f(x) = -2/3(x) + 490
where:
f(x) represents the number of wrap lunch sold.x is the number of sandwich lunch sold.The graph represents the rate of change of the function with respect to the number of sandwich lunch sold.
Part 4.
In this context, we would use an online graphing calculator to plot the linear function as shown in the image attached below.
Part 5.
Assuming Sal's total profit on lunch specials for the next month is $1,593 and the profit amounts remain the same, a system of equations to model this situation is given by:
2x + 3y = 1593; y = -2/3(x) + 531.
2x + 3y = 1,470; y = -2/3(x) + 490.
In conclusion, we can logically deduce that the graphs of the functions for the two months both have the same slope but different y-intercept and x-intercept.
Read more on slope-intercept here: brainly.com/question/7889446
#SPJ1
Complete Question:
Sal's Sandwich Shop sells wraps and sandwiches as part of its lunch specials. The profit on every sandwich is $2, and the profit on every wrap is $3. Sal made a profit of $1,470 from lunch specials last month. The equation 2x + 3y = 1,470 represents Sal's profits last month, where x is the number of sandwich lunch specials sold and y is the number of wrap lunch specials sold.
What is the slope for 5x+2y=6
Answers
Answer:
The slope is -5/2 as a fraction
or -2.5 as a decimal.
Step-by-step explanation:
First we have to get it into this format y = mx + b
5x + 2y = 6 (subtract 5x on both sides)
2y = -5x + 6 (divide by 2 on both sides)
y = -5/2x + 3
The slope is -5/2 or -2.5
Hope this helps ya!!
How many ways can we put 3 math books and 5 English books on a shelf if all the math books must stay together and all the English books must also stay together
Answers
On solving the provided question, we can say that the permutation will bw , N = (4!)(5!)(3!)(3!)= 103,680
what is permutation?The permutation of a set in mathematics is essentially the rearranging of its elements if the set is already ordered, or the arrangement of its members in a linear or sequential order. The act of altering the linear order of an ordered set is referred to as a "permutation" in this context. The mathematical calculation of the number of possible arrangements for a given set is known as permutation. Permutation, in its simplest form, refers to the variety of possible arrangements or orders. The placement of the elements matters with permutations. The placement of items in a specific order is known as a permutation. Here, the set's components are sorted in either chronological order or linear order. like in the case of.
we can put 3 math books and 5 English books on a shelf if all the math books must stay together and all the English books must also stay together will be , N = (4!)(5!)(3!)(3!)= 103,680
To know more about permutation visit:
https://brainly.com/question/1216161
#SPJ4
The algebraic representation of a transformation is (x,y) (3x,3y). This is an example of which type of transformation
Answers
To visualize this transformation, imagine a rectangle with vertices at and (0,2). Applying the transformation (x,y) → \((3x,3y)\) to each vertex, we get a new rectangle with vertices at \((0,0), (3,0), (3,6),\) and \((0,6)\), which is three times the size of the original rectangle.
What form can take Algebraic representations?Algebraic representations can take many forms, including equations, inequalities, functions, and matrices. These representations provide a powerful tool for analysing complex systems and deriving meaningful insights from them.
The algebraic representation \((x,y) (3x,3y)\) describes a dilation transformation, specifically an enlargement or stretch by a scale factor of 3 in both the x and y directions.
This means that every point in the original figure is multiplied by 3 in both the x and y directions, resulting in a larger, similar figure.
To visualize this transformation, imagine a rectangle with vertices at \((0,0), (1,0), (1,2),\) and \((0,2).\) Applying the transformation (x,y) → (3x,3y) to each vertex, we get a new rectangle with vertices at \((0,0), (3,0), (3,6),\) and (0,6), which is three times the size of the original rectangle.
Learn more about rectangle here:
brainly.com/question/29123947
#SPJ1
(a)what does 0.4 + 0.08 equal to ?(b)is 48/10 equal to , less than or greater than 0.48
Answers
Answer:
0.48
Explanation:
\(0.4+0.08=0.48\)\(\frac{48}{10}=4.8\)4.8 is greater than 0.48.
d is the relation defined on r as follows: for every x, y ∈ r, x d y ⇔ xy ≥ 0. determine whether the given relation is reflexive, symmetric, transitive, or none of these. justify your answers.
Answers
This relationship is not transitive, symmetrical, or reflexive.
It is not reflexive because, for any x ∈ R, xd x = xx ≥ 0 is not always true.
It is not symmetric because, for any x,y ∈ R, if xd y = xy ≥ 0, then the reverse is not necessarily true (i.e. yd x = yx ≥ 0).
It is not transitive because, for any x,y,z ∈ R, if xd y = xy ≥ 0 and yd z = yz ≥ 0, then the reverse is not necessarily true (i.e. xd z = xz ≥ 0).
The relation d is defined as xd y ⇔ xy ≥ 0 for all x,y ∈ R. This relation is not reflexive because for any x ∈ R, xd x = xx ≥ 0 is not always true. It is not symmetric because for any x,y ∈ R, if xd y = xy ≥ 0, then the reverse is not necessarily true (i.e. yd x = yx ≥ 0). Lastly, it is not transitive because for any x,y,z ∈ R, if xd y = xy ≥ 0 and yd z = yz ≥ 0, then the reverse is not necessarily true (i.e. xd z = xz ≥ 0). Therefore, the relation d is none of these.
Learn more about reflexive here
https://brainly.com/question/14492876
#SPJ4
what is the probability that the mean lifetime of 25 randomly selected tires of this type will exceed than 42,000 miles?
Answers
The probability that the mean lifetime of 25 randomly selected tires of this type will exceed than 42,000 miles is 25.14.
To break this problem, we need to use the standard normal distribution, assuming that the distribution of tire continuances is roughly normal. We can regularize the value of 42,000 using the formula
z = ( x- μ)/ σ
where x is the value of interest( 42,000 long hauls), μ is the mean tire continuance( 40,000 long hauls), and σ is the standard deviation( 3,000 miles). Plugging in the values, we get
z = ( 42,000- 40,000)/ 3,000 = 0.67
Using a standard normal distribution table or calculator, we can find the probability that an aimlessly named tire will last further than 42,000 long miles by looking up the area to the right of z = 0.67 under the standard average wind. This probability is roughly 25.14.
thus, the probability that a tire named arbitrarily from this brand will last more than 42,000 miles is roughly 25.14.
Learn more about mean;
https://brainly.com/question/1136789
#SPJ4
The correct question is given below-
A particular brand of tires lasts an average of 40,000 miles with a standard deviation of 3,000 miles. What is the probability a tire selected at random lasts more than 42,000 miles?
help me with this please
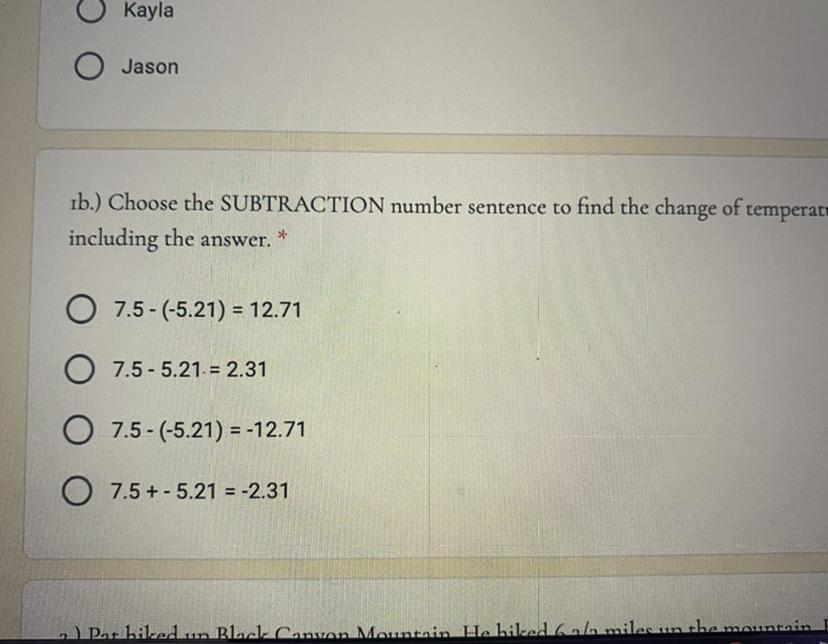
Answers
Write each number in two equivalent forms as fraction, decimal, or percent.
0.29 35% 2/5
show work :D
Answers
Answer:
0.29 = 29% = \(\frac{29}{100}\)
35% = 0.35 = \(\frac{7}{20}\)
\(\frac{2}{5}\)= 0.40 = 40%
Step-by-step explanation:
I need to use the power rule (if m and n are real numbers and x doesn't equal 0, then (x^m)^n = x^mn... ) to simplify this fraction: (2x^2 y^-2 / y^5)^-3
Answers
Answer:
\(= 2x^{-6}y ^{21}\\\\\)
Step-by-step explanation:
Given the indicinal expression (2x^2 y^-2 / y^5)^-3
In indices
\((x^m)^n = x^{mn\)
Applying to solve the question
\((2x^2 y^{-2} / y^5)^{-3}\\\\= \frac{2x^{-6}y^6}{y^{-15}}\\= 2x^{-6} * \frac{y^6}{y^{-15}} \\= 2x^{-6} * y ^{6-(-15)}\\= 2x^{-6} * y ^{6+15}\\= 2x^{-6} * y ^{21}\\= 2x^{-6}y ^{21}\\\\\)
Find the area of the trapezoid.A trapezoid with the top base labeled two feet and the bottom base labeled ten feet. The height is labeled four feet.

Answers
To solve this problem, we will use the following formula for the area of a trapezoid:
\(A=\frac{1}{2}(B+b)h,\)where B and b are the lengths of the bases and h is the height.
Substituting B=10 ft, b=2 ft, and h=4 ft in the above formula, we get:
\(A=\frac{1}{2}(2ft+10ft)4\text{ ft.}\)Simplifying we get:
\(A=24ft^2\text{.}\)Answer:
\(24ft^2\text{.}\)A. Show that the equation represents a circle by rewriting it in standard form.
B. Find the center and radius of the circle.
x2+y2+10y+20=0
Answers
The equation \(x^2 + y^2 + 10y + 20 = 0\) represents a circle with center (0, -5) and radius 5.
To determine if the equation represents a circle, we need to rewrite it in standard form. The standard form of a circle equation is \((x - h)^2 + (y - k)^2 = r^2\), where (h, k) represents the center of the circle and r represents the radius.
Completing the square for the y terms:
\(x^2 + y^2 + 10y + 20 = 0\\ x^2 + y^2 + 10y = -20\\ x^2 + y^2 + 10y + 25 = -20 + 25\\ x^2 + (y + 5)^2 = 5\)
Now the equation is in standard form, \((x - 0)^2 + (y + 5)^2 = 5^2\), which represents a circle.
By comparing the equation to the standard form, we can determine the center and radius of the circle. The center is given by the values (h, k), which in this case is (0, -5). Therefore, the center of the circle is (0, -5).
The radius is determined by the term \(r^2\), which in this case is \(5^2 = 25\). Therefore, the radius of the circle is 5.
In summary, the equation x^2 + y^2 + 10y + 20 = 0 represents a circle with center (0, -5) and radius 5. The completion of the square allowed us to rewrite the equation in standard form, making it evident that it represents a circle. The center of the circle is determined by the values of x and y, and the radius is determined by the value of r.
Learn more about circle equation here:
https://brainly.com/question/29104982
#SPJ11
The perimeter of Dana's rectangular garden is 42 feet. The length of her garden is 6 feet more than twice the width.
A. Define the variables. (1pt)
B. Create an equation(s) that can be used to determine the length and width of the garden. (1pt)
C. What is the length and width of the garden? Show all your work (1pt)
Answers
Answer:
The length is 16 feet, the width is 5 feetStep-by-step explanation:
Given:
The perimeter of the rectangular garden is 42 feetThe length is 6 feet more than twice the widthA. The variables are:
The length - lThe width - wB. The equations are based on given parameters
Use perimeter formula
2(l + w) = 42l = 2w + 6C. Solve the system above by substitution:
2(l + w) = 42l + w = 212w + 6 + w = 213w = 15w = 5Find the value of l:
l = 2*5 + 6 = 16The length is 16 feet, the width is 5 feet
Answer:
The length of the garden is 16 ft while the width of the garden is 5 ft.
Explanation:
a)we want to start with defining the variables.
Let the length of the garden be w.
b) here, we want to create equation
From the question, the length is 6 feet more than twice the width of one garden
Mathematically, we have this as;
\(l = 2w + 6\)
Furthermore, the perimeter is 42 feet
The formula of the perimeter is;
\(2(l + w) = 42\)
Dividing both sides by 2
\(l + w = 21\)
c)Now, we want to solve both equations simultaneously
We can substitute the first equation into the second;
\(2w + 6 + w = 21 \\ 3w + 6 = 21 \\ 3w = 21 - 6 \\ 3w = 15 \\ w = \frac{15}{3} = 5\)
\(l + w = 21 \\ l = 21 - w = 21 - 5 = 16\)
Which statement is NOT true about elements of
the set of rational numbers?
F All integers are elements of the set.
G Elements of the set include repeating and
terminating decimals.
H All elements of the set can be written as a
ratio , where b# 0.
J The numbers i and V3 are elements of the
set.
Answers
Answer:
The numbers i and V3 are elements of the set.
Step-by-step explanation:
The rational numbers are those which can be written as fractions. These are the numbers which can be repeating elements and terminating decimals. All integers can be set of rational numbers. The statements which is not true is statement which states that numbers i and V3 are elements of the set.
how do you say if a number is greater than 0 it equals one but if it's less than 0 it the actual number
Answers
Answer:
If n > 0, then n= 1
If n < 0, then n=n
If you could word this a bit differently, I might be able to help more, but this is what I'm getting from it. The way you worded it is a bit confusing.
Need answers please?!
2(x - 2)² - 5(x - 2) - 5
Answers
The solution of the given equation is 2x² - 13x +13.
What is the solution of the equation?
The collection of all values that, when substituted for unknowns, cause an equation to hold true is known as the solution. Two fundamental algebraic rules using the additive property and the multiplicative property are utilized to determine the solutions for equations needing a single unknown raised to a power of one.
What is the simplification rule?
For those sorts of reasoning that deal with conjunctions, the rule of simplification provides a strong argument. This covers natural deduction, predicate logic, and propositional logic.
Here, we have
Given equation 2(x - 2)² - 5(x - 2) - 5
By applying the simplification rule, we get
= 2(x - 2)² - 5(x - 2) - 5
= 2( x² + 4 - 4x ) - 5x +10 - 5
= 2x² + 8 - 8x - 5x + 5
= 2x² - 13x +13
Hence, the solution of the given equation is 2x² - 13x +13.
To learn more about the simplification rule from the given link
https://brainly.com/question/28452312
#SPJ4
In Exercises 18-21, use Exercise 14 and property 2 of Theorem 5 to test for linear independence in P3. 21. {x} +1, x2 +1, x +1,1} 14. Prove that (1, x,x2,...,x") is a linearly indepen- dent set in P, by supposing that p(x) = (x), where p(x) = do+ax...+x". Next, take successive derivatives as in Example 2. 2. The set Sis linearly independent in V if and only if the set T is linearly inde- pendent in RP.
Answers
The given set S is linearly independent.
To test for linear independence in P3 for Exercise 21, we can use Exercise 14 and property 2 of Theorem 5.
First, we need to suppose that a linear combination of the given set equals zero. Let c1(x+1) + c2(x^2+1) + c3(x+1) + c4(1) = 0, where c1, c2, c3, and c4 are constants. Then, we can simplify this equation to (c1+c3)x^2 + (c1+c2)x + (c1+c3+c4) = 0. This means that the coefficients of the polynomial are all zero, so we can set up a system of equations to solve for the constants:
c1 + c3 = 0
c1 + c2 = 0
c1 + c3 + c4 = 0
Solving this system of equations, we get c1 = c2 = c3 = c4 = 0. Therefore, the set {x+1, x^2+1, x+1, 1} is linearly independent in P3.
For Exercise 14, we need to prove that (1, x, x^2, ..., x^n) is a linearly independent set in Pn. We can do this by supposing that p(x) = a0 + a1x + a2x^2 + ... + anx^n, where a0, a1, a2, ..., an are constants. Then, we can take the successive derivatives of p(x) as follows:
p(x) = a0 + a1x + a2x^2 + ... + anx^n
p'(x) = a1 + 2a2x + ... + nanx^(n-1)
p''(x) = 2a2 + 6a3x + ... + n(n-1)anx^(n-2)
...
p^(n)(x) = n!an
If we suppose that p(x) = (x), then p^(n)(x) = n!. But we know that (1, x, x^2, ..., x^n) is a basis for Pn, so any polynomial in Pn can be written as a linear combination of this basis. Therefore, we can write p(x) as a linear combination of (1, x, x^2, ..., x^n):
p(x) = c0(1) + c1(x) + c2(x^2) + ... + cn(x^n)
Substituting this into p^(n)(x) = n!, we get:
n! = n!cn
cn = 1
Substituting this back into p(x), we get:
p(x) = c0(1) + c1(x) + c2(x^2) + ... + cn(x^n) = c0(1) + c1(x) + c2(x^2) + ... + 1(x^n)
Since we know that (1, x, x^2, ..., x^n) is a basis for Pn, this linear combination can only equal zero if all the constants c0, c1, c2, ..., cn are zero. Therefore, (1, x, x^2, ..., x^n) is a linearly independent set in Pn.
Property 2 of Theorem 5 states that if the set S is linearly independent in V, then the set T obtained by adding a vector not in S to S is also linearly independent in V. In this case, V is RP (the set of real-valued polynomials) and S is the set (1, x, x^2, ..., x^n). So, if we add a vector not in S (for example, x^(n+1)), the resulting set T is also linearly independent in RP.
To learn more about the linearly independent sets visit: brainly.com/question/30720942
#SPJ11
5. What is the range? Explain. (1 point)

Answers
The range of the given graph is [5, ∞).
Range.
Range refers the set of possible output values, and if we have the graph, then the set of all possible y values on the graph is defined as the range.
Given,
Here we have the graph.
Through the given graph we have to find the range of the line.
As per the definition of range, we have identified that the range take the value of y axis.
While we lookin into the given graph, we have identified that the starting point of the line is
=> (0, 5)
In this point 0 refers the x coordinate and 5 refers the y coordinate. So, the starting range is 5.
And the end of the line is not pointed.
So, we can consider that this line goes infinitely.
So, the range of the graph is [5, ∞).
To know more about Range here.
https://brainly.com/question/2709928
#SPJ1
Answer all parts (a)-(e) of this question. The utility of an agent who consumes x amounts of good 1 and y amounts of good 2 is given by the following utility function: U(x,y) = x²y The agent has an income of 12. The price of good 1 is 4 and the price of good 2 is 2. (a) Show that the agent's utility function is homogeneous of degree 3. (b) Explain why the budget constraint is 4x + y = 12 and draw its graph.
(c) Compute the marginal utility the agent derives from good 1 and the marginal utility she derives from good 2. (d) What is the agent's marginal rate of substitution? What is the slope of the budget constraint? (e) Derive the agent's optimal consumption bundle. Illustrate the bundle, along with the budget constraint and the relevant indifference curve, in a diagram on the (x,y) plane and sketch it in x, y space. Interpret the slope of the budget constraint.
Answers
(a) The utility function U(x, y) = x²y is homogeneous of degree 3 because if we multiply both x and y by a positive constant λ, the utility function becomes U(λx, λy) = (λx)²(λy) = λ³x²y. The function exhibits a degree of homogeneity equal to the exponent of λ, which in this case is 3.
(b) The budget constraint can be derived by equating the total expenditure to the agent's income. The price of good 1 is 4, so the expenditure on good 1 is 4x, and the price of good 2 is 2, so the expenditure on good 2 is 2y. Therefore, the budget constraint is given by 4x + 2y = 12. To graph this constraint, we plot x on the horizontal axis and y on the vertical axis. The resulting line has a slope of -2 and intersects the x-axis at x = 3 and the y-axis at y = 6.
(c) To compute the marginal utility of good 1, we take the derivative of the utility function with respect to x, which gives us MU₁(x, y) = 2xy. Similarly, the marginal utility of good 2 is given by MU₂(x, y) = x².
(d) The agent's marginal rate of substitution (MRS) represents the rate at which the agent is willing to trade one good for another while maintaining the same level of utility. It is given by MRS = MU₁/MU₂ = 2xy/(x²) = 2y/x. The slope of the budget constraint is equal to the negative ratio of the prices of the two goods, which is -4/2 = -2.
(e) To derive the agent's optimal consumption bundle, we need to find the combination of x and y that maximizes the agent's utility while satisfying the budget constraint. This occurs at the point where the indifference curve (representing constant utility) is tangent to the budget constraint. In this case, the indifference curve is U(x, y) = x²y, and the optimal consumption bundle can be found by solving the system of equations formed by the utility function and the budget constraint. The resulting bundle will depend on the specific values of x and y obtained. By plotting the bundle on the (x, y) plane along with the budget constraint and an indifference curve, we can visually represent the optimal consumption bundle. The slope of the budget constraint represents the rate at which the agent can trade one good for another while staying within the budget constraint.
Learn more about slope here : brainly.com/question/3605446
#SPJ11
Which inequality is true?
A. I +9< 12
B. 57 > 15
C.
6
27
:> 1
D. 41 - 2 < 10
i need help please
Answers
Answer:
B
Step-by-step explanation:
Answer:
thx for 5 points
Step-by-step explanation:
Work out 0.5 + 1.1 x 1.6
Answers
Answer:
=2.26
Step-by-step explanation:
0.5+1.1x1.6
multiply first (pemdas)
0.5+1.76
add
=2.26
i hope this helps :)
Answer:
0.5 + 1.1 x 1.6 = 2.26
Step-by-step explanation:
check it in a calculator so it's correct