How to prove that these triangles are congruent?
1) a=a1, ha=ha1, ta=ta1
2) ha=ha1, c=c1, hb=hb1
Answers
After answering the presented question,
1) we can conclude that As a triangle result, the two triangles are congruent according to SAS congruence.
2) By the Angle-Side-Angle (ASA) congruence criterion, the two triangles are congruent, and so we have proven that the triangles with altitudes ha, hb, c and ha1, hb1, c1 are congruent.
What is a triangle?A triangle is a closed, double-symmetrical shape composed of three line segments known as sides that intersect at three places known as vertices. Triangles are distinguished by their sides and angles.
To prove that two triangles are congruent, we need to show that all three pairs of corresponding sides and all three pairs of corresponding angles are equal.
To prove that the triangles with sides a, ha, ta and a1, ha1, ta1 are congruent, we can use the Side-Angle-Side (SAS) congruence criterion.
First, we know that a = a1, so the corresponding sides are equal. Then, we need to show that the angles opposite these sides are also equal.
Let angle A be the angle opposite side a and angle A1 be the angle opposite side a1. We know that the altitude from vertex A to side a has length ha, and the altitude from vertex A1 to side a1 has length ha1. Since the triangles are right triangles (since ta and ta1 are altitudes), we have:
sin(A) = ha/a
sin(A1) = ha1/a1
But we know that ha = ha1, so we can write:
sin(A) = sin(A1)
Since both angles are acute, we can conclude that A = A1 or A + A1 = 180 degrees. However, A cannot be equal to 180 degrees (because then ta would not be an altitude), so we must have A = A1.
Therefore, we have shown that the triangles are congruent by the SAS criterion.
To prove that the triangles with altitudes ha, hb, c and ha1, hb1, c1 are congruent, we can use the Hypotenuse-Leg (HL) congruence criterion.
First, we know that ha = ha1, so the corresponding altitudes are equal. Then, we need to show that the hypotenuses and one leg are also equal.
Let side AB be the hypotenuse of the triangle with altitude ha and side A'B' be the hypotenuse of the triangle with altitude ha1. We also know that hb = hb1 and c = c1. Then, we have:
\(|AB| = sqrt(ha^2 + c^2)\\|A'B'| = sqrt(ha1^2 + c1^2)\)
But we know that ha = ha1, c = c1, and hb = hb1, so we can write:
|AB| = |A'B'|
Therefore, we have shown that the hypotenuses are equal. Now, we need to show that one leg is also equal. Let BC be the leg of the triangle with altitude ha and B'C' be the leg of the triangle with altitude ha1.
We know that both triangles are right triangles, so the angle between the hypotenuse and leg is 90 degrees. Also, we know that hb = hb1. Therefore, the triangles share the same hypotenuse, one leg, and the angle between them.
By the Angle-Side-Angle (ASA) congruence criterion, the two triangles are congruent, and so we have proven that the triangles with altitudes ha, hb, c and ha1, hb1, c1 are congruent.
To know more about triangle visit:
brainly.com/question/2773823
#SPJ9
Related Questions
tanx(1+cos2x)=sin2x prove the identity
Answers
Using double angle identity, we are able to prove tan(x)(1 + cos(2x)) = sin(2x).
What is the prove of the given identity?To prove the identity tan(x)(1 + cos(2x)) = sin(2x), we can start by using trigonometric identities to simplify both sides of the equation.
Starting with the left-hand side (LHS):
tan(x)(1 + cos(2x))
We know that tan(x) = sin(x) / cos(x) and that cos(2x) = cos²(x) - sin²(x). Substituting these values, we get:
LHS = (sin(x) / cos(x))(1 + cos²(x) - sin²(x))
Next, we can simplify the expression by expanding and combining like terms:
LHS = sin(x) / cos(x) + sin(x)cos²(x) / cos(x) - sin³(x) / cos(x)
Simplifying further:
LHS = sin(x) / cos(x) + sin(x)cos(x) - sin³(x) / cos(x)
Now, let's work on the right-hand side (RHS):
sin(2x)
Using the double angle identity for sine, sin(2x) = 2sin(x)cos(x).
Now, let's compare the LHS and RHS expressions:
LHS = sin(x) / cos(x) + sin(x)cos(x) - sin³(x) / cos(x)
RHS = 2sin(x)cos(x)
To prove the identity, we need to show that the LHS expression is equal to the RHS expression. We can combine the terms on the LHS to get a common denominator:
LHS = [sin(x) - sin³(x) + sin(x)cos²(x)] / cos(x)
Now, using the identity sin²(x) = 1 - cos²(x), we can rewrite the numerator:
LHS = [sin(x) - sin³(x) + sin(x)(1 - sin²(x))] / cos(x)
= [sin(x) - sin³(x) + sin(x) - sin³(x)] / cos(x)
= 2sin(x) - 2sin³(x) / cos(x)
Now, using the identity 2sin(x) = sin(2x), we can simplify further:
LHS = sin(2x) - 2sin³(x) / cos(x)
Comparing this with the RHS expression, we see that LHS = RHS, proving the identity.
Learn more on trigonometric identity here;
https://brainly.com/question/24496175
#SPJ1
-4=16x what would u do to solve this equation?
Answers
Answer:
x=-1/4
Step-by-step explanation:
-4/16=16x/16
-1/4=x
Match the following. Match the items in the left column to the items in the right column. 1. domain the first element of a relation or function; also known as the input value. 2. output a relation in which every input value has exactly one output value. 3. input the x-value of a function. 4. relation any set of ordered pairs (x, y) that are able to be graphed on a coordinate plane. 5. function the y-value of a function. 6. range the second element of a relation or function; also known as the output value.
Answers
The matching of items and their corresponding descriptions are 1. Domain, 2.Output, 3. Input, 4. Relation, 5. Function, and 6. Range.
What is the appropriate matching of the following items?1. Domain - the first element of a relation or function; also known as the input value.
3. Input - the x-value of a function.
6. Range - the second element of a relation or function; also known as the output value.
4. Relation - any set of ordered pairs (x, y) that are able to be graphed on a coordinate plane.
2. Output - a relation in which every input value has exactly one output value.
5. Function - the y-value of a function.
learn more about domain of a function: https://brainly.com/question/1369616
#SPJ9
Solve for x in the diagram below

Answers
Answer:
X=6
Step-by-step explanation:
5x+(x+54)=90
6x+54=90
6x=36
X=6
Order of operation
(8+4x7) divide 18=
Please explain step by step to get marked as brainliest

Answers
7x4=28+8=36
(36)divided by 18 =2
P=parentheses
E= can’t remember but doesn’t apply
M=multiply
D=divide
A=add
S=subtraction
Solve the equation in that order.
Obv we can’t divide as soon as pemdas show
So, 1st solve parentheses first.
8+4x7
1st multiply 4x7= 28
Then add 8
Which equals 36
36 divided by 18 = 2
Check answer 18+18=36
is 1 over 3 = to 3 out of 3
Answers
the correct answer is No
Step-by-step explanation:
it's not equal
Answer:
\(\frac{1}{3}\neq\frac{3}{3}\)
Step-by-step explanation:
The two numbers are different
NO LINKS!! URGENT HELP PLEASE!!!
Express the statement as an inequality part 2 c^2
a. The negative of z is not greater than 6
1. z ≤ 6
2. -z ≤ 6
3. z ≤ -6
4. -z < 6
5. z < 6
b. The negative of m is not less than -6
1. m ≤ -6
2. m < -6
3. -m < -6
4. m < 6
5. -m ≥ -6
Answers
Symbol notation
< means "less than".> means "greater than".≤ means "less than or equal to".≥ means "greater than or equal to".= means "equals".A negative real number is any real number that is less than zero.
A positive real number is any real number that is greater than zero.
Zero is neither positive nor negative.
(a) The negative of z is not greater than 6
If the negative of z is not greater than 6, then it is less than or equal to 6.
-z ≤ 6.
(b) The negative of m is not less than -6
If the negative of z is not less than -6, then it is greater than or equal to -6.
-m ≥ -6.
-z ≤ 6
b. The negative of m is not less than -6 can be written as:
-m ≥ -6
Three-fourths of the yard is covered with grass and one-fourth is used as a garden. The sprinkler could only water 1/5 of the yard, so the rest died. Use the model to find out how much of the grass died.
Answers
3/5 or 60% of the grass died because the sprinkler could only water 1/5 of the yard.
Let's start by breaking down the information given:
- Three-fourths of the yard is covered with grass.
- One-fourth of the yard is used as a garden.
- The sprinkler could only water 1/5 of the yard.
To find out how much of the grass died, we need to determine the portion of the grass that was not watered by the sprinkler.
Let's assume the total area of the yard is represented by the value 1. Therefore, we can calculate the area of the grass as 3/4 of the total yard, which is (3/4) * 1 = 3/4.
The sprinkler can only water 1/5 of the yard, so the portion of the grass that was watered is (1/5) * (3/4) = 3/20.
To find the portion of the grass that died, we subtract the watered portion from the total grass area:
Portion of grass that died = (3/4) - (3/20) = 15/20 - 3/20 = 12/20.
Simplifying, we get:
Portion of grass that died = 3/5.
Therefore, 3/5 or 60% of the grass died because the sprinkler could only water 1/5 of the yard.
for more such question on grass visit
https://brainly.com/question/6204338
#SPJ8
Allison bought jelly beans to share with her friends. She bought pounds of blueberry jelly beans and pounds of lemon jelly beans. If she gave pounds of jelly beans away to her friends, how many pounds of jelly beans does Allison have left?
Answers
Answer: \(1\dfrac{11}{12}\text{ pounds}\)
Step-by-step explanation:
The complete question is provided in the attachment.
Given, Amount blueberry jelly beans= \(1\dfrac{1}{4}\) pounds
\(=\dfrac{5}{4}\) pounds.
Amount lemon jelly beans = \(2\dfrac{1}{3}\)pounds
\(=\dfrac{7}{2}\) pounds
Total jelly beans she bought = Amount blueberry jelly beans + Amount lemon jelly beans
\(=(\dfrac{5}{4}+\dfrac{7}{3})\) pounds
\(=\frac{15+28}{12}\text{ pounds}\\\\=\dfrac{43}{12}\text{ pounds}\)
Amount of jelly beans she gave away = \(1\dfrac{2}{3}=\dfrac{5}{3}\text{ pounds}\)
Amount of jelly beans she has left= Total jelly beans - Amount of jelly beans she gave away
=\(\dfrac{43}{12}-\dfrac{5}{3}\\\\=\dfrac{43-20}{12}\\\\=\dfrac{23}{12}\\\\=1\dfrac{11}{12}\text{ pounds}\)
She has left \(1\dfrac{11}{12}\text{ pounds}\) of jelly beans.

What is the base of a triangle that has a height of 6 centimeters and an area of 18 centimeters? Use the formula h = StartFraction 2 A Over b EndFraction, where A represents the area of the triangle, h represents the height, and b represents the length of the base. One-third centimeter Two-thirds centimeters 3 Centimeters 6 Centimeters
Answers
Answer:
The base is 6cm
Step-by-step explanation:
Using \(\frac{1}{2}\)bh=area, you just plug in 6 for h and 18 for area and solve. The formula should be 3b=18, which equals 6
The solution is Option D.
The length of the base of the triangle is B = 6 cm
What is a Triangle?A triangle is a plane figure or polygon with three sides and three angles.
A Triangle has three vertices and the sum of the interior angles add up to 180°
Let the Triangle be ΔABC , such that
∠A + ∠B + ∠C = 180°
The area of the triangle = ( 1/2 ) x Length x Base
For a right angle triangle
From the Pythagoras Theorem , The hypotenuse² = base² + height²
if a² + b² = c² , it is a right triangle
if a² + b² < c² , it is an obtuse triangle
if a² + b² > c² , it is an acute triangle
Given data ,
Let the area of the triangle be represented as A
Now , the value of A = 18 cm²
Let the base of the triangle be B
Let the height of the triangle be H = 6 cm
Now , area of the triangle = ( 1/2 ) x Length x Base
Substituting the values in the equation , we get
18 = ( 1/2 ) x B x 6
18 = 3B
Divide by 3 on both sides of the equation , we get
B = 6 cm
Hence , the base length of the triangle is B = 6 cm
To learn more about triangles click :
https://brainly.com/question/16739377
#SPJ6
Find the slope of the line shown in the graph below enter your answer as a simplified improper fraction if necessary

Answers
The slope is 1
Explanation:Choose the points (2, -3) and (4, -1)
The slope is:
\(\begin{gathered} y=\frac{-1-(-3)}{4-2}=\frac{-1+3}{4-2} \\ \\ =\frac{2}{2}=1 \end{gathered}\)Marin has used 4 face wipes from the pack of 20 that she just bought. What percent of the face wipes did she use?
Answers
20%
1. 4 divided by 20 = 0.2
2. 0.2 times 100 = 20
3. And the final answer is 20%
Hope that helped:)
givin: 3x<-9 choose the solution set

Answers
Answer: X < -3
Sean says the value of a to the -3rd power is always less than 1 if a is positive.
Christine says the value of a to the -3rd power is always less than 1 when a is negative
Which one is correct, and for the one that is incorrect enter the number that proves in to be incorrect (if none say none).
Answers
Sean's statement is correct. Christine's statement is incorrect when a is negative.
The value of a to the -3rd power is always less than 1 if a is positive.
For example, if a = 2, then a to the -3rd power is 1/8, which is less than 1. Therefore, Sean's statement is correct.
The value of a to the -3rd power is always less than 1 if a is positive, but it is always greater than 1 if a is negative.
For example, if a = 2, then a to the -3rd power is 1/8, which is less than 1. But if a = -2, then a to the -3rd power is -1/8, which is greater than 1.
Therefore, Christine's statement is incorrect when a is negative.
Learn more about the numbers here:
https://brainly.com/question/28691894
#SPJ1
Give the equation of the line
with a slope of 3 that goes
through the point (2,-1)
Answers
Answer:
y=3x-7
Step-by-step explanation:
y-y1=m(x-x1)
y-(-1)=3(x-2)
y+1=3(x-2)
y+1=3x-6
y=3x-6-1
y=3x-7
Please mark me as Brainliest if you're satisfied with the answer.
According to the quantity equation, changes in the money supply will lead directly to changes in the price level if velocity and real GDP are unaffected by the change in the money supply. Will velocity change over time? What factors might lead to changes in velocity? Are those changes related to changes in the money supply?
Answers
Velocity is not constant over time and can be influenced by a variety of factors. Changes in velocity can have implications for the relationship between changes in the money supply and the price level, highlighting the complexity of monetary dynamics in an economy.
According to the quantity equation (MV = PQ), changes in the money supply (M) will lead directly to changes in the price level (P) if velocity (V) and real GDP (Q) remain constant. However, velocity is not necessarily constant over time and can be influenced by various factors.
Velocity represents the rate at which money circulates in the economy, indicating how quickly money is used to facilitate transactions. It is influenced by factors such as changes in consumer and business behavior, technological advancements, financial innovation, and shifts in confidence and trust in the economy.
Changes in velocity can occur due to several reasons. For example:
Changes in Transaction Patterns: Shifts in consumer preferences or business practices can alter the frequency and speed of transactions, affecting how money circulates and influencing velocity.
Financial Innovation: Advancements in payment systems, such as the rise of electronic transactions, online banking, or mobile payments, can potentially impact the velocity of money by facilitating faster and more efficient transactions.
Confidence and Economic Stability: Changes in economic conditions, inflation expectations, or financial stability can influence people's willingness to hold money, affecting velocity.
Monetary and Fiscal Policies: Changes in monetary policy, such as interest rate adjustments or changes in the money supply, can indirectly affect velocity by influencing borrowing and spending behavior.
While changes in velocity can occur independently of changes in the money supply, they can also be related. For instance, if the money supply increases without a corresponding increase in the demand for money (velocity decreases), it can put upward pressure on prices. On the other hand, if velocity increases due to changes in transaction patterns or increased economic activity, it can offset the impact of changes in the money supply on prices.
Overall, velocity is not constant over time and can be influenced by a variety of factors. Changes in velocity can have implications for the relationship between changes in the money supply and the price level, highlighting the complexity of monetary dynamics in an economy.
for such more question on Velocity
https://brainly.com/question/16763767
#SPJ8
Arrange the steps in order to simplify the expression

Answers
Answer:
Step-by-step explanation:
For step explanation:
1. write the problem
2. distinguishing the neg sign
3. distributing 3
4. moving like terms next to each other through commutative property
5. Combining like terms
6. getting rid of parentheses

A clothing factory makes t-shirts. If each machine makes 3 iş t-shirts per hour, how many t-shirts does one machine make in 4 hours
Answers
Answer: 12
Step-by-step explanation:
3 x 4 = 12
-6x+ 3 times 2x=16 solve for x
Answers
x = 2.67 is the solution to the equation -6x + (3)(2x) = 16.
What is the Algebraic Equations?
Algebraic equations are mathematical statements that describe a relationship between two or more variables, where one variable is expressed in terms of the others.
To solve the equation -6x + (3)(2x) = 16, we can simplify the expression on the left-hand side first:
-6x + (3)(2x) = -6x + 6x = 0x = 0
Next, we isolate the x term on one side of the equation by subtracting 16 from both sides:
0x = 0 - 16 = -16
Finally, we can solve for x by dividing both sides of the equation by -6:
x = -16 / -6 = 2.67 (rounded to two decimal places).
So, x = 2.67 is the solution to the equation -6x + (3)(2x) = 16.
To learn more about Algebraic Equations, Visit
https://brainly.com/question/4344214
#SPJ1
4b - 3(6 + 2b) = 12
i
Answers
Answer:
-15
Step-by-step explanation:
4b - 3(6 + 2b) = 12
4b - 18 - 6b = 12
4b - 6b = 12 + 18
-2b = 30
b = 30/-2
b = -15
According to this diagram, what is tan 62 degrees ?
Answers
Answer:
According to this diagram, the tan 62 degrees, is the ratio of the opposite side and the adjacent side of the triangle which is equal to 1.875 units.
What is the right angle triangle property?
In a right-angle triangle ratio of the opposite side to the adjacent side is equal to the tangent angle between the adjacent side and the hypotenuse side.
Here, (b) is the opposite side, (a) is the adjacent side, and is the angle made between the adjacent side and the hypotenuse side.
The sides of the triangle are 8, 15, and 17 units long and the measure of the angles of the right angle triangle is 62, 90, and 28 degrees.
Re-draw, the Here in the given triangle, the base is the side which is 15 units long. Re-draw the triangle as shown below.
In the attached triangle below, the opposite side of the triangle is 15 units and the adjacent side of the triangle is 8 units long.
The angle between the opposite side and the adjacent side is 62 degrees. Thus using the right angle triangle property as,
Thus, according to this diagram, the tan 62 degrees, is the ratio of the opposite side and the adjacent side of the triangle which is equal to 1.875 units.
Learn more about the right-angle triangle property here;
brainly.com/question/22790996
in a data set consisting of 30 positive integers, the minimum value is 13. the number 6 is added to the original set to create a set of 31 positive integers. which of the following measures must be 7 greater for the new data set than for the original data set?
a. The mean
b. The median
c. The range
d. The standard deviation
Answers
The mean, median, range, and standard deviation for the new data set must all be 7 greater than for the original data set.
The mean is the sum of all the values divided by the number of values. Adding the number 6 to the original data set of 30 positive integers increases the sum of all the values by 6, which means the mean for the new data set must be 7 greater than the mean for the original data set.
The formula for the mean is: Mean = (Sum of Values)/(Number of Values)
For the original data set: Mean = (Sum of Values)/30
For the new data set: Mean = (Sum of Values + 6)/31
Therefore, the mean for the new data set must be 7 greater than the mean for the original data set.
The median is the middle value in a set of data. Adding the number 6 to the original data set of 30 positive integers increases the total number of values to 31, which means the median is calculated differently for the new data set than the original data set. The median for the new data set must be 7 greater than the median for the original data set.
The formula for the median is: Median = (n+1)/2
For the original data set: Median = (30+1)/2 = 15.5
For the new data set: Median = (31+1)/2 = 16.5
Therefore, the median for the new data set must be 7 greater than the median for the original data set.
The range is calculated by subtracting the smallest value from the largest value in a data set. Adding the number 6 to the original data set of 30 positive integers increases the largest value by 6, which means the range for the new data set must be 7 greater than the range for the original data set.
The formula for the range is: Range = (Largest Value) - (Smallest Value)
For the original data set: Range = (Largest Value) - 13
For the new data set: Range = (Largest Value + 6) - 13
Therefore, the range for the new data set must be 7 greater than the range for the original data set.
The standard deviation is a measure of how spread out the values in a data set are. Adding the number 6 to the original data set of 30 positive integers increases the total number of values by 1, which means the standard deviation for the new data set must be 7 greater than the standard deviation for the original data set.
The formula for the standard deviation is: Standard Deviation = √ (Sum of (Values - Mean)2 / Number of Values)
For the original data set: Standard Deviation = √ (Sum of (Values - Mean)2 / 30)
For the new data set: Standard Deviation = √ (Sum of (Values - Mean)2 / 31)
Therefore, the standard deviation for the new data set must be 7 greater than the standard deviation for the original data set.
The mean, median, range, and standard deviation for the new data set must all be 7 greater than for the original data set
Learn more about standard deviation here:
https://brainly.com/question/23907081
#SPJ4
Is anyone good at geometry if so can someone help me please ?
NO LINKS PLEASE

Answers
Answer:
1366.66 ft³
Step-by-step explanation:
12ft × 8ft × 12ft = 1152 ft³
214.66 ft³ + 1152 ft³
1366.66 ft³
Answer:
The total volume of the trailer is 1366.6 ft^3
Step-by-step explanation:
12 * 8 = 96
96 * 12 = 1152 ft^3
1152ft^2 + 214.66 = 1366.6 ft^3
sorry I was late.
If you deposit $2000 in an account earning 3% interest compounded monthly, how much will you have in the account in 20 years?
Answers
Given the exponential function f (x) and the logarithmic function g(x), which of the following statements is true?
a. As x→∞, f (x)→∞ and g(x)→∞.
b. As x→∞, f (x)→∞ and g(x)→1.
c. As x→∞, f (x)→3 and g(x)→1.
d. As x→∞, f (x)→3 and g(x)→∞.
HELP!!! ASAP!!! PRE-CALCULUS!!!

Answers
Answer:
a
Step-by-step explanation:
Both the exponential and logarithmic functions tend to infinity.
Six students write an exam. The average score obtained on the exam by the group of students is 71%. If the first two students each obtained a mark of 73%, while the next three students each obtained a mark of 68%, what was the mark obtained by the sixth student?
Answers
The first two students obtained a mark of 73%, which gives us a total of 73 + 73 = 146 marks.
The next three students obtained a mark of 68% each, which gives us a total of 68 + 68 + 68 = 204 marks.
The average score obtained by the group is 71%. Since there are six students, the total marks obtained by all six students would be 6 * 71 = 426 marks.
To find the mark obtained by the sixth student, we can subtract the total marks obtained by the first five students from the total marks obtained by all six students: 426 - (146 + 204) = 76 marks.
Therefore, the mark obtained by the sixth student is 76%.
The profit P, in dollars, of selling x widgets and y gadgets is given by the function P(x, y) = 7x + 3y. Which corner point of the shaded region will maximize the profit?
A. (10, 30)
B. (15, 25)
C. (0, 35)
D. (20, 15)
Answers
Step-by-step explanation:
The answer is B
Answers is B
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
What is the length of AD?'
Use the given information to complete the worksheet.
Thank you!
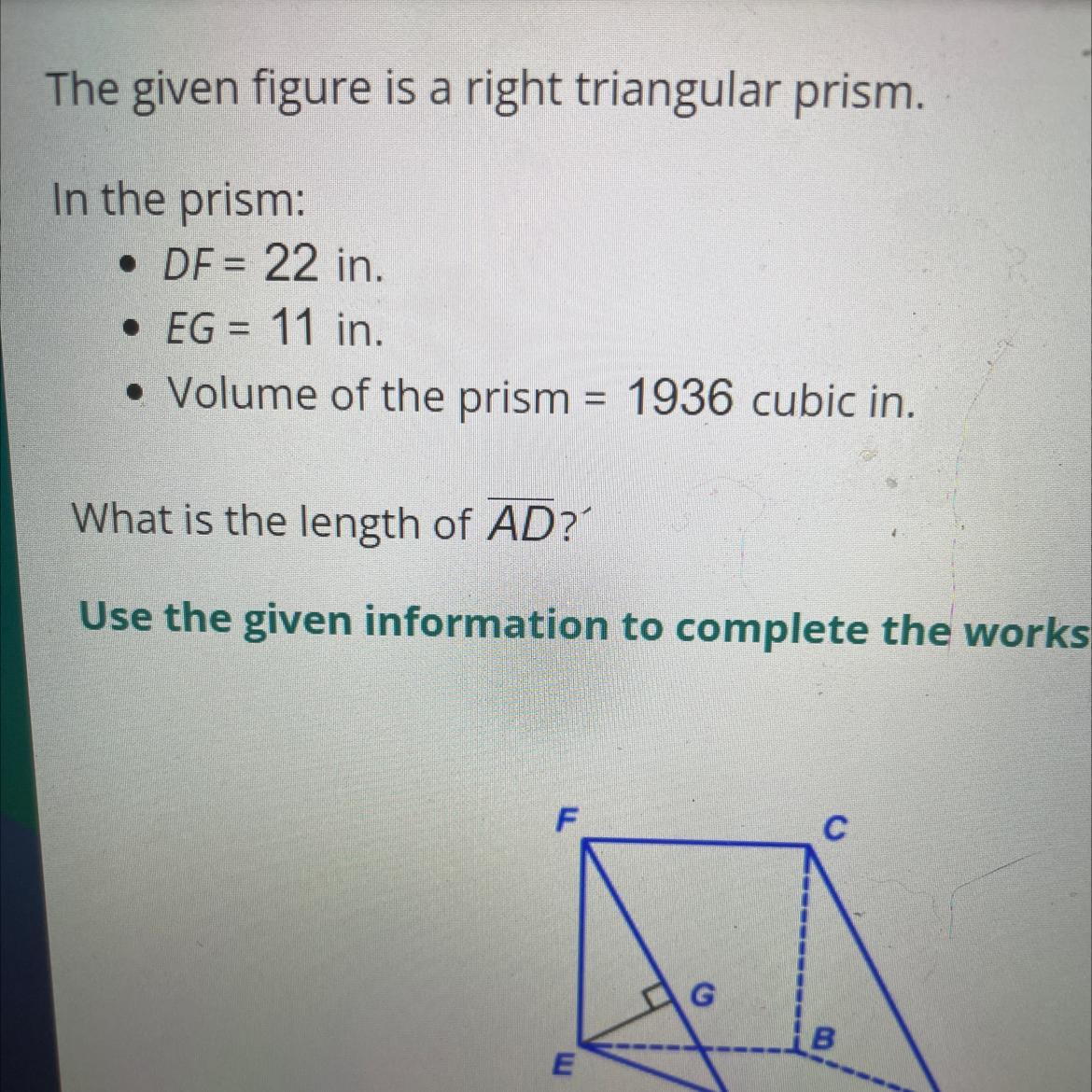
Answers
The length of side AD is,
⇒ AD = 16
We have to given that;
The given figure is a right triangular prism.
In the prism:
• DF = 22 in.
• EG = 11 in.
• Volume of the prism = 1936 cubic in.
Since, Volume of right triangular prism is,
V = 1/2 (bh) x L
Substitute all the values we get;
V = 1/2 (22 × 11) × AD
1936 = 121 × AD
AD = 16
Thus, The length of side AD is, 16
Learn more about the multiplication visit:
https://brainly.com/question/10873737
#SPJ1
Suppose that an object is dropped from a height of h meters and hits the ground with a velocity of v meters per second. Then v= \(\sqrt{x} 19.6h\). If an object hits the ground with a velocity of 25.7 meters per second, from what height was it dropped?
Answers
If an object hits the ground with a velocity of 25.7 meters per second, it was dropped from a height of 33.7 meter .
In the question ,
it is given that
the when the object is dropped from height h then the velocity with which it hits the ground is given by the formula
v = √(19.6×h)
to find the height it was dropped , and it hits the ground with velocity 25.7 meter per second ,
we substitute v = 25.7 in the equation v = √(19.6×h) ,
we get ,
25.7 = √(19.6×h)
squaring both the sides , we get
19.6 × h = 25.7²
19.6 × h = 660.49
h = 660.49/19.6
h = 33.698
h ≈ 33.7
Therefore ,If an object hits the ground with a velocity of 25.7 meters per second, it was dropped from a height of 33.7 meter .
The given question is incomplete , the complete question is
Suppose that an object is dropped from a height of h meters and hits the ground with a velocity of v meters per second. Then v = √(19.6×h) . If an object hits the ground with a velocity of 25.7 meters per second, from what height was it dropped?
Learn more about Equation here
https://brainly.com/question/20359474
#SPJ1
determine the inverse of the function

Answers
Answer:
\(f^{-1}(x)= \dfrac{1}{2}\ln \left(-\dfrac{x^2}{x^2-1}\right), \quad \textsf{for}\:\{x:0 < x < 1\}\)
Step-by-step explanation:
Given function:
\(f(x)=\dfrac{e^x}{\sqrt{e^{2x}+1}}\)
The domain of the given function is unrestricted: {x : x ∈ R}
The range of the given function is restricted: {f(x) : 0 < f(x) < 1}
To find the inverse of a function, swap x and y:
\(\implies x=\dfrac{e^y}{\sqrt{e^{2y}+1}}\)
Rearrange the equation to make y the subject:
\(\implies x\sqrt{e^{2y}+1}=e^y\)
\(\implies x^2(e^{2y}+1)=e^{2y}\)
\(\implies x^2e^{2y}+x^2=e^{2y}\)
\(\implies x^2e^{2y}-e^{2y}=-x^2\)
\(\implies e^{2y}(x^2-1)=-x^2\)
\(\implies e^{2y}=-\dfrac{x^2}{x^2-1}\)
\(\implies \ln e^{2y}= \ln \left(-\dfrac{x^2}{x^2-1}\right)\)
\(\implies 2y \ln e= \ln \left(-\dfrac{x^2}{x^2-1}\right)\)
\(\implies 2y(1)= \ln \left(-\dfrac{x^2}{x^2-1}\right)\)
\(\implies 2y= \ln \left(-\dfrac{x^2}{x^2-1}\right)\)
\(\implies y= \dfrac{1}{2}\ln \left(-\dfrac{x^2}{x^2-1}\right)\)
Replace y with f⁻¹(x):
\(\implies f^{-1}(x)= \dfrac{1}{2}\ln \left(-\dfrac{x^2}{x^2-1}\right)\)
The domain of the inverse of a function is the same as the range of the original function. Therefore, the domain of the inverse function is restricted to {x : 0 < x < 1}.
Therefore, the inverse of the given function is:
\(f^{-1}(x)= \dfrac{1}{2}\ln \left(-\dfrac{x^2}{x^2-1}\right), \quad \textsf{for}\:\{x:0 < x < 1\}\)