Answers
A function that is positive in the entire interval [-3, -2] is -x² - 5x - 5.
How do you determine a function's positive and negative intervals?calculating the positive and negative gaps from a graph sketch. Drawing a rough sketch of a polynomial's graph based on the polynomial's end behaviour and the multiplicities of its zeros is another method for determining the periods over which it is positive or negative.
f(x) = -2x - 1 will be our first function to examine.
f(-3) = -2(-3) - 1 = 5
f(-2) = -2(-2) - 1 = 3
Now, let's try the second function, g(x) = x² - 2x - 3.
g(-3) = (-3)² - 2(-3) - 3 = 9 + 6 - 3 = 12
g(-2) = (-2)² - 2(-2) - 3 = 4 + 4 - 3 = 5
Finally, let's try the third function, h(x) = x³ - 4x² + 5x - 2.
h(-3) = (-3)³ - 4(-3)² + 5(-3) - 2 = -27 - 36 - 15 - 2 = -80
h(-2) = (-2)³ - 4(-2)² + 5(-2) - 2 = -8 - 16 - 10 - 2 = -36
We cannot conclude that this function is positive for the full range [-3, -2] because h(-3) and h(-2) are both negative.
To know more about function visit:-
https://brainly.com/question/12431044
#SPJ1
Related Questions
professor smith ran a simple regression equation using midterm exam scores to predict final exam scores. the r square was 0.91 and this was statistically significant (p
Answers
The the final exam score according to the linear equation is 69. Thus, Option A is correct.
According to the statement
we have to find that the exam of the midterm which is Y with the help of the given equation.
So, For this purpose, we know that the
The value of p is 0.0001 and the given equation is Y=1.5 + .9(75).
Which is a linear equation.
So,
A linear equation is an algebraic equation of the form y=mx+b. involving only a constant and a first-order (linear) term, where m is the slope and b is the y-intercept.
So, From given equation
Y=1.5 + .9(75).
Solve this equation
Y = 1.5 + 67.5
Y = 69.
So, The the final exam score according to the linear equation is 69. Thus, Option A is correct.
Learn more about Linear equation here
https://brainly.com/question/4074386
Disclaimer: This question was incomplete. Please find the full content below.
Question:
Professor Smith ran a simple regression equation using midterm exam scores to predict final exam scores. The R square was 0.91 and this was statistically significant (p=0.0001). Using the following simple regression equation generated by Professor Smith, predict the final exam score Y when the midterm score is 75: Y=1.5 + .9(75).
A. 69
B. 55
C. 82
D. 91
#SPJ4
ken drinks 1/6 of a carton of milk each day. how much milk does he drink in 3 days?
Answers
Answer:
half a carton
Step-by-step explanation:
1/6 x 3/1 = 3/6 or 1/2
you could also add 1/6 + 1/6 + 1/6
A. A population of values has a normal distribution with μ=208.5 and σ=35.4. You intend to draw a random sample of size n=236.
Find the probability that a single randomly selected value is greater than 203.4.
P(X > 203.4) = Round to 4 decimal places.
Find the probability that the sample mean is greater than 203.4.
P(X¯¯¯ > 203.4) = Round to 4 decimal places.
B. A population of values has a normal distribution with μ=223.7 and σ=56.9. You intend to draw a random sample of size n=244.
Find the probability that a single randomly selected value is between 217.5 and 234.6.
P(217.5 < X < 234.6) = Round to 4 decimal places.
Find the probability that the sample mean is between 217.5 and 234.6.
P(217.5 < X¯¯¯ < 234.6) = Round to 4 decimal places.
Answers
A. Using the given information, we can standardize the value 203.4 using the formula \(z = (X - μ) / σ\), where X is the value of interest, μ is the mean, and σ is the standard deviation.
Thus, we get: \(z = (203.4 - 208.5) / 35.4 = -0.14407\)
Using a standard normal distribution table or calculator, we can find the probability that a randomly selected value is greater than \(203.4\):
\(P(X > 203.4)\) = \(P(Z > -0.14407)\) = \(0.5563\) (rounded to 4 decimal places)
To find the probability that the sample mean is greater than 203.4, we need to use the central limit theorem, which states that the sample mean of a large enough sample size (n >= 30) from a population with any distribution has a normal distribution with mean μ and standard deviation σ / sqrt(n). Thus, we get:
\(z = (203.4 - 208.5) / (35.4 / sqrt(236))\)\(= -1.3573\)
Using a standard normal distribution table or calculator, we can find the probability that the sample mean is greater than 203.4:
\(P(X¯¯¯ > 203.4) = P(Z > -1.3573)\)= \(0.0867\) (rounded to 4 decimal places)
B. Using the given information, we can standardize the values \(217.5\) and \(234.6\) using the same formula as before. Thus, we get:
\(z1 = (217.5 - 223.7) / 56.9\) \(= -0.10915\)
\(z2 = (234.6 - 223.7) / 56.9 = 0.19235\)
Using a standard normal distribution table or calculator, we can find the probability that a randomly selected value is between 217.5 and 234.6:
\(P(217.5 < X < 234.6) = P(-0.10915 < Z < 0.19235) = 0.2397\) (rounded to 4 decimal places)
To find the probability that the sample mean is between 217.5 and 234.6, we can use the same formula as before, but with the sample size and population parameters given in part B. Thus, we get:
\(z1 = (217.5 - 223.7) / (56.9 / sqrt(244)) = -1.0784\)
\(z2 = (234.6 - 223.7) / (56.9 / sqrt(244)) = 1.7256\)
Using a standard normal distribution table or calculator, we can find the probability that the sample mean is between 217.5 and 234.6:
\(P(217.5 < X¯¯¯ < 234.6) = P(-1.0784 < Z < 1.7256)\)= \(0.8414\)(rounded to 4 decimal places)
To learn more about standard normal distribution, visit here
https://brainly.com/question/29509087
#SPJ4
Walltown is 25 miles east of Park City.
- Park City is 38 miles south of Edenton,
• Michael drove from Edenton to Park City and then to Walltown.
- Leah drove straight from Edenton to Walltown
About how much farther
did Michael drive than Leah
5 miles
25 miles
34 miles
45.5 miles
TRA
WUNNIN
Answers
Answer:
Since Michael traveled 63 miles while Leah traveled 45.48 miles, Michael traveled 17.51 extra miles.
Step-by-step explanation:
Given that Walltown is 25 miles east of Park City, and Park City is 38 miles south of Edenton, and Michael drove from Edenton to Park City and then to Walltown while Leah drove straight from Edenton to Walltown, to determine about how much farther did Michael drive than Leah, the following calculation must be performed, using the Pythagorean theorem:
Michael:
38 + 25 = 63
Leah:
25 ^ 2 + 38 ^ 2 = X ^ 2
625 + 1,444 = X ^ 2
2,069 = X ^ 2
√2,069 = X
45.48 = X
63 - 45.49 = 17.51
Therefore, since Michael traveled 63 miles while Leah traveled 45.48 miles, Michael traveled 17.51 extra miles.
I don't understand this. Can Someone please help?

Answers
Answer:
A. -∞ < x < ∞
Step-by-step explanation:
The domain of a function is the set of all possible inputs (x values). We see from the graph that the function extends forever to the left and to the right. Thus, the domain of the function is all real numbers, as the function extends on the x-axis towards positive and negative infinity. A. represents this fact.
In your own words, explain how to find the rate of change of the following graph at x=1. Then find the rate of change at x=1.

Answers
Answer:
Rate of change of the graph = 1
Step-by-step explanation:
Rate of change of the graph at any point is defined by the slope of the line at that point.
Since, slope of a line between two points \((x_1,y_1)\) and \((x_2,y_2)\) is given by,
m = \(\frac{y_2-y_1}{x_2-x_1}=\frac{\triangle y}{\triangle x}\)
In other words, slope of a line between two points is given by the ratio of rise and run of the line between the given points.
Therefore, slope of the line passing through two points (0, 2) and (1, 3) will be,
m = \(\frac{3-2}{1-0}\)
m = 1
Rate of change at x = 1 is 1.
45 POINTS -Find the perpendicular line. Don’t explain

Answers
By analytical geometry, the line y = - 2 · x - 1 represents a line perpendicular to the line shown in the picture. (Correct choice: C)
How to find the equation of a line perpendicular to another line
According to analytical geometry, lines are described by polynomials of the form:
y = m · x + b
Where:
m - Slopeb - Interceptx - Independent variable.y - Dependent variable.And the equation of the perpendicular line pass through a point of original line and is related to the slope of the line by following relationship:
m · m' = - 1
Where:
m - Slope of original line.m' - Slope of perpendicular line.First, determine the slope and intercept of the original line:
(x, y) = (0, 1)
1 = m · 0 + b
b = 1
(x, y) = (2, 0)
0 = m · 2 + b
2 · m + b = 0
m = - b / 2
m = - 1 / 2
Second, calculate the slope of the perpendicular line:
m' = 1 / (- 1 / 2)
m' = - 2
Third, we conclude by discarding options that the equation of the perpendicular line is y = - 2 · x - 1.
To learn more on perpendicular lines: https://brainly.com/question/21167969
#SPJ1
An Isosceles triangle has two congruent sides. the first side is expressed by x+2 and the second side is expressed by 2x-25 what is the value of X
Answers
The value of x is 27
How to determine the value
From the information given, we have that the triangle is an isosceles triangle.
The properties of an isosceles triangle are;
It has two equal sidesTwo equal anglesIt has three edges and three verticesSum of internal angles is 180We have that;
First side = x + 2
Second side = 2x - 25
Equate the two sides, we get;
x+ 2 = 2x - 25
collect like terms
x - 2x = - 25 - 2
subtract like terms
-x= -27
make 'x' the subject
x = 27
Hence, the value is 27
Learn more about isosceles triangles here:
https://brainly.com/question/1475130
#SPJ1
anybody solve this i made it its easy
3(55x2) + 9 + 44 +88 x 9 = your number + 163593
Answers
Answer:
165*6+53+792= 990+845 = 1,835
Step-by-step explanation:
a relation that contains no repeating groups and has nonkey columns solely dependent on the primary key but contains determinants is in which normal form?
Answers
A relation that contains no repeating groups and has nonkey columns solely dependent on the primary key but contains determinants is in the third normal form (3NF).
In this form, every monkey column of the relation is determined by the primary key and has no transitive dependencies on any other monkey column. This means that every column in the relation is uniquely identified by the primary key, and there are no redundant data in the relation. Therefore, the relation is free from anomalies such as update, deletion, and insertion anomalies. The third normal form is considered the most commonly used normal form in the relational database design, and it ensures data integrity and consistency. In summary, a relation that meets the criteria mentioned in the question is in 3NF.
To know more about columns visit:
https://brainly.com/question/29194379
#SPJ11
30
200
y - 200+ 0.50x
y = 50 + 0.30x
Consider the data shown on the graph.
• The y-intercept represents the base price of $ drag and drop answer here for airfare from NYC
• The slope represent a cost of drag and drop answer here cents per mile traveled.
• If the base cost for airfare changed to $50 and the cost per mile is unchanged, the new equation would be drag and drop answer here
• If the cost per mile changed to 50 cents, the new equation would be drag and drop answer here
Answers
Answer:
Step-by-step explanation:
THE ANSWER IS 200 , 30, Y=50+0.30X, Y=200+ 0.50X
The solution is, x = 20, is the solution of Y=0.25x +50=0.30x+ 40.
What is equation?An equation is a mathematical statement that is made up of two expressions connected by an equal sign. In its simplest form in algebra, the definition of an equation is a mathematical statement that shows that two mathematical expressions are equal.
here, we have,
EXPLANATION
The equation given can be express as
y = 0.25x + 50
y = 0.30x + 40
Since, both equations are functions
Equate the two functions together
0.25x + 50 = 0.30x + 40
Collect the like terms
0.25x - 0.30x = 40 - 50
x(0.25 - 0.30) =-10
x(-0.5) = -10
-0.5x = -10
Divide both sides by -0.5
-0.5x / -0.5 = -10/-0.5
x = 10/0.5
x = 20
When collecting the like terms, we isolate values with the same variables from values with a different variables.
If a positive sign crosses an equality sign it automatically becomes a negative sign and if a negative sign crosses an equality operator it automatically becomes a positive sign.
Hence, The solution is, x = 20, is the solution of Y=0.25x +50=0.30x+ 40.
To learn more on equation click:
brainly.com/question/24169758
#SPJ2
complete question:
Y=0.25x +50=0.30x+ 40 how would I get x=20?
For the linear regression y = ẞ1 + ẞ2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 +681 +382 + 18ẞ1ẞ2
Derive the partial derivatives of SSE with respect to B1 and B2 and solve the optimal values of these parameters.
a. B₁ = B1
b. B₂ =
Answers
The optimal values of these parameters are:
a. β₁ = 0
b. β₂ = 0
The linear regression y = β1 + β2x + e, assuming that the sum of squared errors (SSE) takes the following form:
SSE = 382 + 681 + 382 + 18β1β2
Derive the partial derivatives of SSE with respect to β1 and β2 and solve the optimal values of these parameters.
Given that SSE = 382 + 681 + 382 + 18β1β2 ∂SSE/∂β1 = 0 ∂SSE/∂β2 = 0
Now, we need to find the partial derivative of SSE with respect to β1.
∂SSE/∂β1 = 0 + 0 + 0 + 18β2 ⇒ 18β2 = 0 ⇒ β2 = 0
Therefore, we obtain the optimal value of β2 as 0.
Now, we need to find the partial derivative of SSE with respect to β2. ∂SSE/∂β2 = 0 + 0 + 0 + 18β1 ⇒ 18β1 = 0 ⇒ β1 = 0
Therefore, we obtain the optimal value of β1 as 0. Hence, the partial derivative of SSE with respect to β1 is 18β2 and the partial derivative of SSE with respect to β2 is 18β1.
Thus, the optimal values of β1 and β2 are 0 and 0, respectively.
Therefore, the answers are: a. β₁ = 0 b. β₂ = 0
Learn more about regression analysis at
https://brainly.com/question/31691955
#SPJ11
what is the probability that more than 5 patients arrive at the hospital with flu-like symptoms between 12:00pm and 12:20pm?
Answers
Answer: X 0 1 2 3 4 5 6 7 8 P(X=k) 0.05 0.07 0.13 0.12 0.20 0.25 0.07 0.03 0.08 the probability that more than 5 patients arrive at the hospital
What is the probability that more than 5 patients arrive at the hospital with flu-like symptoms between 12:00pm and 12:20pm?
Step-by-step explanation:
Group of answer choices
A. 0.43
B. 0.18
C. 0.82
D. 1
Part two of the question:
using the same information as stated before,
Match the probability statements with the correct probabilities.
(choose one answer)
The probability that X is less than or equal to 5.
A. 0.82 B. 0 C. 0.05 D. 0.48 E. 0.64 F. 1 G. 0.08 H. 0.52
The probability that X is greater than 7.
A. 0.82 B. 0 C. 0.05 D. 0.48 E. 0.64 F. 1 G. 0.08 H. 0.52
The probability that X is between 3 (noninclusive) and 7 (noninclusive).
A. 0.82 B. 0 C. 0.05 D. 0.48 E. 0.64 F. 1 G. 0.08 H. 0.52
The probability that no patients arrive in that interval.
A. 0.82 B. 0 C. 0.05 D. 0.48 E. 0.64 F. 1 G. 0.08 H. 0.52
Maya owes $104,000 to a credit card company. The debt grows with 12% annual interest that compounds every month. How much will Maya owe in three years?
Answers
Simple One-time Interest
I = P0r
A = P0 + I = P0 + P0r = P0(1 + r)
Instructions: For the given discriminant, state the number and type of solutions.

Answers
If the discriminant is negative, then neither of the solutions is a real number.
Since the discriminant is a negative number 7, then there is/are no real solutions to the quadratic equation.
When renting a car, the cost per mile is inversely proportional to the number of miles driven. At Zippy Car Rentals, if the standard model car is driven for 300 miles, then the cost per mile is $0.25.
At Zippy Car Rentals, the constant of variation is
for a standard car rental. If that rental car is driven for 375 miles, then the cost per mile is $
.
Answers
Answer:
.20 per mile.
Step-by-step explanation:
300 x .25 is 75. 75/375 is .20
The cost for painting a shed is 8,00. If the dimensions of a similar shed are havled, what would the cost be for painting the reduced sized shed?
Answers
Answer:
4
Step-by-step explanation:
8/2=4
6 ft
8 ft
452.16 ft
150.72 ft
48 ft
904.32 ft

Answers
Answer:
The answer is 904.778 \(ft^3\).
Step-by-step explanation:
-You first need the formula for the volume of a cylinder:
\(V = \pi r^2h\)
-Take the radius and the height of the cylinder for the formula:
\(V = \pi 6^2 8\)
-Then, you solve the formula:
\(V = \pi 6^2 8\)
\(V = \pi \times 6^2 \times 8\)
\(V = \pi \times 36 \times 8\)
\(V = \pi \times 288\)
\(V = 288\pi \approx 904.778\)
So, the answer is 904.778 \(ft^3\).
Given that a randomly chosen flight arrives in los angeles (lax), what is the probability that the carrier is american airlines (aa)?
Answers
Using concepts of probability, it exists found that there exists a 4.7% probability that it arrives at American airlines (aa).
What is probability?A probability exists given by the number of expected outcomes divided by the number of total outcomes.
Over a large number of trials, a percentage can also define the probability of a single event.
In this question, analyzing the problem on the internet, we have that over a considerable number of flights, of those which came on time, 4.7% of them were in American airlines.
There exists a 4.7% probability that it arrives on American airlines(aa).
To learn more about probability refer to:
brainly.com/question/15536019
#SPJ4
Answer: 2316/16924 = 0.137 = 13.7%
Step-by-step explanation:
Let's say you rolled a dice twice, and you got at least a 6. What is the probability that the sum of both rolls is at least 9
Answers
The probability that the sum of both rolls is at least 9 is 2/36.
Probability is the chance that a given event will occur. the ratio of the number of outcomes in an exhaustive set of equally likely outcomes that produce a given event to the total number of possible outcomes.
Given:
Total sample spaces: 36.
Number on one dice: 6
For sum of both rolls to be 9 , the only possible way is (6,3)(3,6)
Using probability formula,
Thus The probability that the sum of both rolls is at least 9 is 2/36.
To Learn more about Probability visit:
https://brainly.com/question/4313883
#SPJ4
At the grocery store ,8 oranges cost $4 what is the cost for 9 oranges ?
Answers
Answer:
$4.50
Step-by-step explanation:
First step is to find the price per orange. You can do this by dividing total cost by oranges bought. See below.
\(4 \div 8 \\ = .50\)
Now to find the amount of 9 oranges, you'd multiply price per orange by the specified amount needed (so 9)
\(9 \times .50 \\ = 4.50\)
Find the slope
Y=-5x-1
Answers
Answer:
-5
Step-by-step explanation:
y=mx+b
m is the slope
y=-5x-1
the slope is -5
Answer:
-5
Step-by-step explanation:
.
do you expect a large or a small t-statistic if the population means are different? explain.
Answers
A large t-statistic indicates a greater difference between the sample means and provides stronger evidence for a significant difference between the populations.
Why would we expect a large t-statistic if the population means are different?The t-statistic is a measure of the difference between two sample means relative to the variability within the samples. When the population means are different, the difference between the sample means will tend to be larger, which will result in a larger numerator in the t-statistic formula. The larger the difference between the sample means, the greater the evidence for a difference between the populations. In contrast, if the population means are similar, the difference between the sample means will be smaller, resulting in a smaller numerator and a weaker test of significance.
The denominator of the t-statistic formula is the standard error of the mean, which measures the variability of sample means around the population mean. If the sample size is large enough, the standard error of the mean will be small, resulting in a smaller denominator and a larger t-statistic. Therefore, when the population means are different, a larger t-statistic would be expected due to a combination of a larger numerator and a smaller denominator.
In summary, If the population means are different, a large t-statistic would be expected.
Learn more about t-statistic
brainly.com/question/15236063
#SPJ11
Find and classify the critical points of z = (x² - 7x) (y² - 3y) Local maximums: Local minimums: Saddle points: For each classification, enter a list of ordered pairs (x, y) where the max/min/saddle occurs. If there. are no points for a classification, enter DNE.
Answers
The critical points are:
Local maximums:(7/2, 3/2)
Local minimums: DNE
Saddle points: (0, 0), (7,3) , (0,3) , (7,0).
To find and classify the critical points of the function z = (x² - 7x) (y² - 3y) :
1. Take the partial derivatives of z with respect to x and y:
∂z/∂x = (2x - 7) (y² - 3y)
∂z/∂y = (x² - 7x) (2y - 3)
2. Set the partial derivatives equal to zero and solve the resulting equations simultaneously to find the critical points:
(2x - 7) (y² - 3y) = 0
(x² - 7x) (2y - 3) = 0
3. The critical points occur when either one or both of the partial derivatives are zero.
(2x - 7) (y² - 3y) = 0 which gives us possibilities: x = 7/2, y=0 and y= 3.
(x² - 7x) (2y - 3) = 0 which gives us possibilities: y = 3/2, x=0 and x= 7. -
4. Now we evaluate the function at these critical points to determine their nature.
At (x, y) = (0, 0), (7,3) , we get, the value of z = (x² - 7x) (y² - 3y) is 0
(0,3) , (7,0), we get, the value of z = (x² - 7x) (y² - 3y) is < 0
and, at (7/2, 3/2) we get, the value of z = (x² - 7x) (y² - 3y) is > 0
and, zₓₓ = -9/2 < 0, which indicates a local maximum.
Therefore, the critical points are:
Local maximums:(7/2, 3/2)
Local minimums: DNE
Saddle points: (0, 0), (7,3) , (0,3) , (7,0).
Learn more about critical points:
brainly.com/question/32077588
#SPJ4
A. The monthly electrical utility bills of all customers for Blue Ridge Electric are known to be distributed normally with a mean equal to $80.00 a month and a population standard deviation of $36.00. If a sample of n = 100 customers is selected at random, what is the probability that the average bill for those sampled will exceed $75.00?
a. -1.39.
b. 0.0823.
c. 0.9177.
d. 0.8795
Answers
The given information is as follows: The population mean is \($μ = 80$\)Population standard deviation is \($σ = 36$\)Sample size is $n=100$.
We are required to find the probability that the average bill for those sampled will exceed\($75.00$\).
This problem requires to find the probability of a sample mean. Since the sample size is greater than 30, we can use the normal distribution. Since the population standard deviation is known, we will use a normal distribution, not a t-distribution.
The formula for sample mean is:
\($Z =\frac{\bar{x} - \mu}{\frac{\sigma}{\sqrt{n}}}$\)Where,\($\bar{x}$\)= sample mean\($\mu$\) = population meanσ = population standard deviation n = sample size.
Substituting the values in the formula, we get: \($Z =\frac{\bar{x} - \mu}{\frac{\sigma}{\sqrt{n}}} = \frac{75-80}{\frac{36}{\sqrt{100}}}=-1.39$.\)
So, the probability that the average bill for those sampled will exceed \($75.00$\) is \($0.9177$\).Therefore, option (c) 0.9177 is correct.
Hence, the probability that the average bill for those sampled will exceed \($75.00$\) is 0.9177.
To know more about probability :
brainly.com/question/31828911
#SPJ11
if you are tossing a six-sided die, what is the probability of getting either a 1 or a 2 on your first toss and your second toss?
Answers
It is based on the likelihood of something occurring. The reasoning behind probability is the foundation of theoretical probability. The probability of getting one or two in first and second toss is \(\frac{1}{9}\).
Probability is a number that represents the likelihood or chance that an event will occur. Probabilities can be expressed as proportions ranging from 0 to 1, as well as percentages ranging from 0% to 100%.
The probability of getting one or two in first toss will be:-
\(\frac{1}{6} + \frac{1}{6} = \frac{1+1}{6} = \frac{2}{6} = \frac{1}{3}\) ( as the probability of getting one in first toss is \(\frac{1}{6}\) and getting two is also \(\frac{1}{6}\)).
Similarly the probability of getting one or two in second toss will be:-
\(\frac{1}{6} +\frac{1}{6} = \frac{1+1}{6} = \frac{2}{6} = \frac{1}{3}\)
The total probability of getting one or two in first and second toss will be:-
\(\frac{1}{3} *\frac{1}{3} = \frac{1}{9}\)
Hence, Henceprobability is \(\frac{1}{9}\).
Go through the given link below to know more about probability:-
https://brainly.com/question/13604758
#SPJ4
ASAP
And I hope everyone day is good

Answers
Answer:
7
Step-by-step explanation:
When dividing numbers with exponents that have the same base (in this case it’s 5), you can subtract the two exponents to simplify it.
I’m just going to show you how to solve it for you to understand:
\(\frac{5^{11} }{5^{x} }=5^{4}\) This means that what can you subtract from 11 (the exponent) to get to 4 (the other exponent). You can notice that 11 - 7 = 4.
So,
\(\frac{5^{11} }{5^{7} }=5^{4}\)
Answer: 7
You have a good day too!
Hope this helps! :)
If a one-way between-subjects ANOVA involved 48 people, and one independent variable with 5 levels/conditions, what would be the critical value of F if using an alpha of .01?CHOOSE ONEA. 2.589B. 3.737C. 3.476D. 3.790
Answers
The critical value of F for a one-way between-subjects ANOVA with 4 and 43 degrees of freedom (5 levels minus 1, and 48 total participants minus 5 levels) at an alpha level of .01 is approximately 3.737.
To calculate the critical value of F, we need to use a statistical table or calculator. The F distribution table with 4 and 43 degrees of freedom at an alpha level of .01 gives a critical value of 3.737.
This means that if the calculated F value for the ANOVA is greater than 3.737, we can reject the null hypothesis at the .01 level of significance.
It's important to note that the critical value of F changes depending on the degrees of freedom and the alpha level chosen.
In this case, we have 5 levels/conditions and 48 participants, but if the sample size or number of levels changes, the critical value of F would be different.
To know more about value click here
brainly.com/question/30760879
#SPJ11
the mean number of words per minute (wpm) read by sixth graders is 89 with a standard deviation of 16 wpm. if 66 sixth graders are randomly selected, what is the probability that the sample mean would be greater than 92.25 wpm? round your answer to four decimal places.
Answers
With a 0.98% chance, the sample mean would be more than 5.09 WPM off from the population mean.
What Is Normal probability distribution?
Normal distribution of probabilities
The z-score formula is used to solve problems involving samples with normally distributed data.
The zscore of a measure X in a set with mean and standard deviation is given by:
z = X-μ/σ
The Z-score calculates the deviation of the measure from the mean in standard deviations. We glance at the z-score table after determining the Z-score to determine the p-value connected to it. The likelihood that the measure's value is less than X, or the percentile of X, is represented by this p-value. The likelihood that the value of the measure exceeds X is calculated by deducting 1 from the pvalue.
Theorem of central limits
The Central Limit Theorem establishes that a large sample size can be approximated to a normal distribution with mean for a random variable X with mean and standard deviation.
In this problem, we have that:
μ = 89 , σ = 16 , n=66 , s = \(\frac{16}{\sqrt{66} }\) = 1.97
How likely is it that the sample mean will be more than 92.25 WPM population mean?
X = 92.25
z = X-μ/σ
By the Central Limit Theorem
σ = s
Z = 92.25 - 89 / 1.97
Z = 1.6497 has pvalue = 0.049502
Hence probabitlity is 0.0495
Learn more about Normal probability distribution at
https://brainly.com/question/23887199
#SPJ4
Please help ASAP !!!
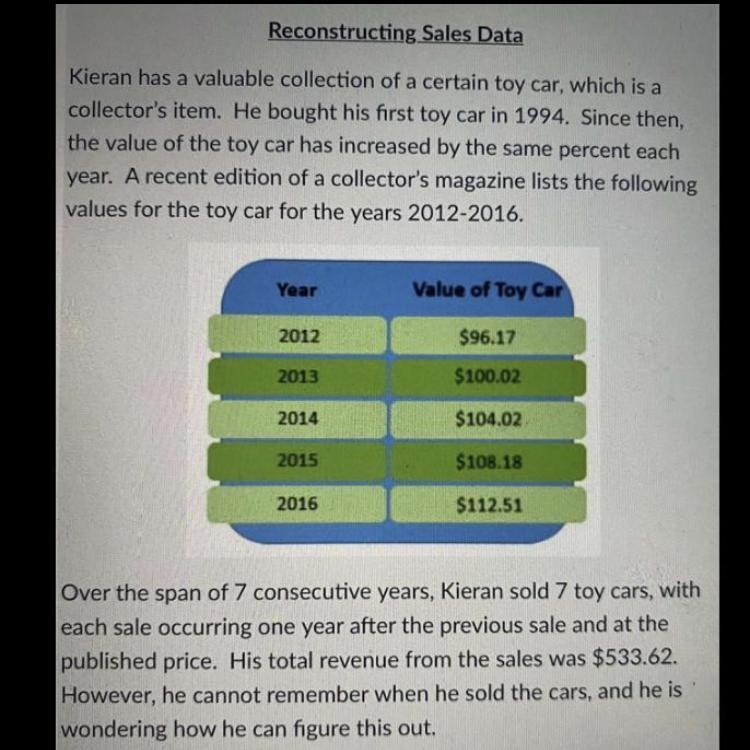
Answers
Answer: What do you need help with?
Step-by-step explanation: I don’t understand.
