Answers
Step-by-step explanation:
\(6.\)
\( \frac{1}{2} = \frac{1.5}{3} \: \: \: \: \: Less \: \: Than \: \frac{2}{3} \)
\( \frac{8}{12} = \frac{2}{3} \: \: \: \: \: Equal \: \: To \: \frac{2}{3} \)
\( \frac{3}{8} = \frac{1.125}{3} \: \: \: \: \: Less \: \: Than \: \frac{2}{3} \)
\( \frac{10}{15} = \frac{2}{3} \: \: \: \: \: Equal \: \: To \: \frac{2}{3} \)
\( \frac{4}{5} = \frac{2.4}{3} \: \: \: \: \: Greater \: \: Than \: \frac{2}{3} \)
\( \frac{9}{10} = \frac{2.7}{3} \: \: \: \: \: Greater \: \: Than \: \frac{2}{3} \)
\(7.\)
\(Kenny = \frac{1}{8} \)
\(Gail = \frac{2}{4} \)
\( \frac{1}{8} ? \frac{2}{4} \)
\(\frac{1}{8} ? \frac{2 \times 2}{4 \times 2} \)
\( \frac{1}{8} < \frac{4}{8} \)
\( \frac{1}{8} < \frac{2}{4} \)
\(Gail \: \: ate \: \: more \: \: than \: \: Kenny\)
Related Questions
One number is 7 less than a second number.Twice the second number is 2 less than 4 time the first
Answers
Can someone pls help me with this its sooo confusing

Answers
9514 1404 393
Answer:
$189.32
Step-by-step explanation:
Add all of the numbers shown to the beginning balance to find the ending balance.
$92.19 -39.35 +49.76 +87.35 +9.97 -10.60 = $189.32
Tristan's balance at the end of the month was $189.32.
__
There should be no confusion. Money deposited into the account increases the balance by the amount deposited.
Money spent from the account decreases the balance by the amount spent.
Here, amounts deposited are given a plus sign (+); amounts spent are given a minus sign (-).
__
Additional comment
It can be tedious to enter these numbers correctly into a calculator. Many folks prefer a calculator that provides a "tape", a record of the amounts and operations the calculator uses in the computation. Alternatively, you can put the numbers in a spreadsheet and use the SUM function to do the addition for you. That, too, makes it easy to check that numbers have been entered correctly.
The attachment shows the calculation done in a spreadsheet.

Forty percent of all Americans who travel by car look for gas stations and food outlets that are close to or visible from the highway. Suppose a random sample of n=25 Americans who travel by car are asked how they determine where to stop for food and gas. Let x be the number in the sample who respond that they look for gas stations and food outlets that are close to or visible from the highway.
a. What are the mean and variance of x?
b. Calculate the interval μ±2σμ±2σ. What values of the binomial random variable x fall into this interval?
c. Find P(6≤≤x$\leq$14). How does this compare with the fraction in the interval μ±2σμ±2σ for any distribution? For mound-shaped distributions?
Answers
Answer:
Explained below.
Step-by-step explanation:
Let the random variable X be defined as the number of Americans who travel by car look for gas stations and food outlets that are close to or visible from the highway.
The probability of the random variable X is: p = 0.40.
A random sample of n =25 Americans who travel by car are selected.
The events are independent of each other, since not everybody look for gas stations and food outlets that are close to or visible from the highway.
The random variable X follows a Binomial distribution with parameters n = 25 and p = 0.40.
(a)
The mean and variance of X are:
\(\mu=np=25\times 0.40=10\\\\\sigma^{2}=np(1-p)-25\times0.40\times(1-0.40)=6\)
Thus, the mean and variance of X are 10 and 6 respectively.
(b)
Compute the values of the interval μ ± 2σ as follows:
\(\mu\pm 2\sigma=(\mu-2\sigma, \mu+ 2\sigma)\)
\(=(10-2\cdot\sqrt{6},\ 10+2\cdot\sqrt{6})\\\\=(5.101, 14.899)\\\\\approx (5, 15)\)
Compute the probability of P (5 ≤ X ≤ 15) as follows:
\(P(5\leq X\leq 15)=\sum\limits^{15}_{x=5}{{25\choose x}(0.40)^{x}(1-0.40)^{25-x}}\)
\(=0.0199+0.0442+0.0799+0.1199+0.1511+0.1612\\+0.1465+0.1140+0.0759+0.0434+0.0212\\\\=0.9772\)
Thus, 97.72% values of the binomial random variable x fall into this interval.
(c)
Compute the value of P (6 ≤ X ≤ 14) as follows:
\(P(6\leq X\leq 14)=\sum\limits^{14}_{x=6}{{25\choose x}(0.40)^{x}(1-0.40)^{25-x}}\)
\(=0.0442+0.0799+0.1199+0.1511+0.1612\\+0.1465+0.1140+0.0759+0.0434\\\\=0.9361\\\\\approx P(5\leq X\leq 15)\)
The value of P (6 ≤ X ≤ 14) is 0.9361.
According to the Tchebysheff's theorem, for any distribution 75% of the data falls within μ ± 2σ values.
The proportion 0.9361 is very large compared to the other distributions.
Whereas for a mound-shaped distributions, 95% of the data falls within μ ± 2σ values. The proportion 0.9361 is slightly less when compared to the mound-shaped distribution.
Probabilities are used to determine the chance of an event.
\(\mathbf{Mean = 10}\) and \(\mathbf{Variance = 6}\).97.72% values of the binomial random variable x fall into the interval \(\mathbf{\mu \pm 2\sigma}\).93.61% values of the binomial random variable x fall into the interval 6 to 14The given parameters are:
\(\mathbf{n = 25}\)
\(\mathbf{p = 40\%}\)
(a) Mean and variance
The mean is calculated as follows:
\(\mathbf{Mean = np}\)
\(\mathbf{Mean = 25 \times 40\%}\)
\(\mathbf{Mean = 10}\)
The variance is calculated as follows:
\(\mathbf{Variance = np(1 - p)}\)
So, we have:
\(\mathbf{Variance = 25 \times 40\%(1 - 40\%)}\)
\(\mathbf{Variance = 6}\)
(b) The interval \(\mathbf{\mu \pm 2\sigma}\)
First, we calculate the standard deviation
\(\mathbf{\sigma = \sqrt{Variance}}\)
\(\mathbf{\sigma = \sqrt{6}}\)
\(\mathbf{\sigma = 2.45}\)
So, we have:
\(\mathbf{\mu \pm 2\sigma = 10 \pm 2 \times 2.45}\)
\(\mathbf{\mu \pm 2\sigma = 10 \pm 4.90}\)
Split
\(\mathbf{\mu \pm 2\sigma = 10 + 4.90\ or\ 10 - 4.90}\)
\(\mathbf{\mu \pm 2\sigma = 14.90\ or\ 5.10}\)
Approximate
\(\mathbf{\mu \pm 2\sigma = 15\ or\ 5}\)
So, we have:
\(\mathbf{\mu \pm 2\sigma = (5,15)}\)
The binomial probability is then calculated as:
\(\mathbf{P = ^nC_x p^x \times (1 - p)^{n - x}}\)
This gives
\(\mathbf{P = ^{25}C_5 \times (0.4)^5 \times (1 - 0.6)^{25 - 5} + ...... +^{25}C_{15} \times (0.4)^{15} \times (1 - 0.6)^{25 - 15}}\)
\(\mathbf{P = 0.0199 + ..... + 0.0434 + 0.0212}\)
\(\mathbf{P = 0.9772}\)
Express as percentage
\(\mathbf{P = 97.72\%}\)
This means that; 97.72% values of the binomial random variable x fall into the interval \(\mathbf{\mu \pm 2\sigma}\)
\(\mathbf{(c)\ P(6 \le x \le 14)}\)
The binomial probability is then calculated as:
\(\mathbf{P = ^nC_x p^x \times (1 - p)^{n - x}}\)
So, we have:
\(\mathbf{P = ^{25}C_6 \times (0.4)^6 \times (1 - 0.4)^{25 - 6} + ...... +^{25}C_{14} \times (0.4)^{14} \times (1 - 0.4)^{25 - 14}}\)
\(\mathbf{P = 0.0422 +.............+0.0759 + 0.0434}\)
\(\mathbf{P = 0.9361}\)
This means that:
93.61% values of the binomial random variable x fall into the interval 6 to 14
By comparison, 93.61% is very large compared to the other distributions., and the proportion 93.61 is slightly less when compared to the mound-shaped distribution.
Read more about binomial probability at:
https://brainly.com/question/19578146
After you place the order for 15 shirts, one of the members asks if he can order 2 more shirts, how much will it cost for the 2 extra shirts.
Answers
Answer:
???
Notes:
Hi, sorry, but I can't really do this if I don't know what 15 shirts cost, or if there isn't an equation of some sort. (Sorry again...)
Cakculate the Length of line x
Answers
The length of line x in the figure of the cube given is 19.
Calculate the length of the base of the cube, which is the diagonal of the lower sides :
base length = √10² + 6²
base length = √136
The length of x is the diagonal of the cube
x = √baselength² + 15²x = √(√136)² + 15²
x = √136 + 225
x = √361
x = 19
Therefore, the length of line x in the figure given is 19.
Learn more on length : https://brainly.com/question/23008020
#SPJ1

Two gamblers have a big pile of money on the table. They will each draw one card from a regular deck of 52 cards, and the gambler with the highest card will win the money. If their cards are of equal value, they will split the pot. What is the probability that they split the pot?
Answers
In order to get both equal cards, the first gambler can get any card, but the second gambler has to get a card of the same value, that probability is 4/52 (there are 4 cards of the same value on the 52 card deck)
Answer:
4/52 = 0.07692307692 ==> 7.7%
That is approximatelly 7.7%
Yes, I'm still here
Do you see
What is the mean for the set of data? Pls help i will give brainliest

Answers
Answer:
3.3
Step-by-step explanation:
all the numbers add up to 33
and there is 10 numbers so divide 33 by 10 and you get 3.3
Does anyone know how to solve this with steps?
Find the savings plan balance after 19 months with an APR of 11% and monthly payments of $250.
Answers
To solve the savings plan balance, we have to calculate the interest for 19 months. The formula for calculating interest for compound interest is given below:$$A = P \left(1 + \frac{r}{n} \right)^{nt}$$where A is the amount, P is the principal, r is the rate of interest, t is the time period and n is the number of times interest compounded in a year.
The given interest rate is 11% per annum, which will be converted into monthly rate and then used in the above formula. Therefore, the monthly rate is $r = \frac{11\%}{12} = 0.0091667$.
The monthly payment is $PMT = $250. We need to find out the amount after 19 months. Therefore, we will use the formula of annuity.
$$A = PMT \frac{(1+r)^t - 1}{r}$$where t is the number of months of the plan and PMT is the monthly payment. Putting all the values in the above equation, we get:
$$A = 250 \times \frac{(1 + 0.0091667)^{19} - 1}{0.0091667}$$$$\Rightarrow
A = 250 \times \frac{1.0091667^{19} - 1}{0.0091667}$$$$\Rightarrow
A =250 \times 14.398$$$$\Rightarrow A = 3599.99$$
Therefore, the savings plan balance after 19 months with an APR of 11% and monthly payments of $250 is $3599.99 (approx).
For such more question on months
https://brainly.com/question/5010192
#SPJ8
Determine coordinates of D on trapezium when A(-2;-2) and Cc(-3/4;-6) and midpoint of AD(-1/2;3)
Answers
The coordinates of D on the trapezium is (1, 8)
How to determine the coordinates of D on the trapezium?The coordinates are given as
A = (-2,-2)
C = (-3/4, -6)
Midpoint AD = (-1/2,3)
The midpoint is calculated as
Midpoint = 1/2 * (x1 + x2, y1 + y2)
So, we have the following:
Midpoint AD = 1/2 * (x1 + x, y1 + y)
This gives
(-1/2, 3) = 1/2 * (-2 + x, -2 + y)
Multiply through the equation by 2
So, we have
(-1, 6) = (-2 + x, -2 + y)
Evaluate the values of x and y in the equations
So, we have
-2 + x = -1
-2 + y = 6
This gives
x = 1
y = 8
So, we have
D = (1, 8)
Hence, the coordinates of D on the trapezium is (1, 8)
Read more about midpoints at
https://brainly.com/question/25886396
#SPJ1
Trey has bought 10 pounds of dog food. He feeds his dog
pounds for each meal. For how many meals will the food last?
Write your answer in simplest form
Answers
how many pounds does he feed his dogs for each meal?
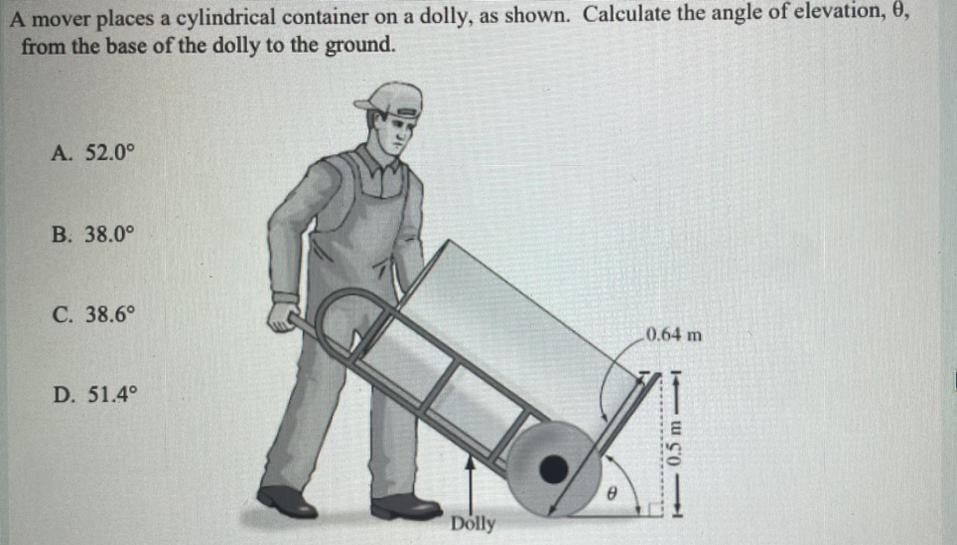
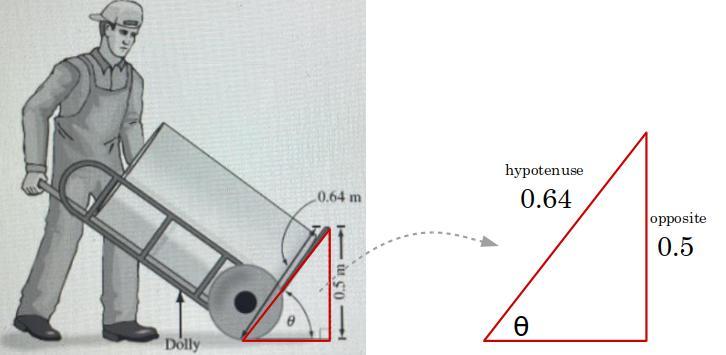
A mover places a cylindrical container on a dolly, as shown. Calculate the angle of elevation, U,
from the base of the dolly to the ground.
A. 52.0°
B. 38.0°
C. 38.6°
D. 51.4°
Answers
Check the picture below.
\(\sin( \theta )=\cfrac{\stackrel{opposite}{0.5}}{\underset{hypotenuse}{0.64}} \implies \sin^{-1}(~~\sin( \theta )~~) =\sin^{-1}\left( \cfrac{0.5}{0.64} \right) \\\\\\ \theta =\sin^{-1}\left( \cfrac{0.5}{0.64} \right)\implies \theta \approx 51.4^o\)
Make sure your calculator is in Degree mode.
Which linear function has the same y-intercept as the one that is represented by the graph?
On a coordinate plane, a line goes through points (3, 4) and (5, 0).
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 3, negative 1, 1, 3. Column 2 is labeled y with entries negative 4, 2, 8, 14.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 4, negative 2, 2, 4. Column 2 is labeled y with entries negative 26, negative 18, negative 2, 6.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 5, negative 3, 3, 5. Column 2 is labeled y with entries negative 15, negative 11, 1, 5.
A 2-column table with 4 rows. Column 1 is labeled x with entries negative 6, negative 4, 4, 6. Column 2 is lab
eled y with entries negative 26, negative 14, 34, 46.
Answers
The linear function that has the same y-intercept as the given graph is the equation y = -2x + 10, corresponding to option 3.
To determine the linear function with the same y-intercept as the graph, we need to find the equation of the line passing through the points (3, 4) and (5, 0).
First, let's find the slope of the line using the formula:
slope (m) = (change in y) / (change in x)
m = (0 - 4) / (5 - 3)
m = -4 / 2
m = -2
Now that we have the slope, we can use the point-slope form of a linear equation to find the equation of the line:
y - y1 = m(x - x1)
Using the point (3, 4) as our reference point, we have:
y - 4 = -2(x - 3)
Expanding the equation:
y - 4 = -2x + 6
Simplifying:
y = -2x + 10
Now, let's check the given options to find the linear function with the same y-intercept:
Option 1: The table with x-values (-3, -1, 1, 3) and y-values (-4, 2, 8, 14)
The y-intercept is not the same as the given line. So, this option is not correct.
Option 2: The table with x-values (-4, -2, 2, 4) and y-values (-26, -18, -2, 6)
The y-intercept is not the same as the given line. So, this option is not correct.
Option 3: The table with x-values (-5, -3, 3, 5) and y-values (-15, -11, 1, 5)
The y-intercept is the same as the given line (10). So, this option is correct.
Option 4: The table with x-values (-6, -4, 4, 6) and y-values (-26, -14, 34, 46)
The y-intercept is not the same as the given line. So, this option is not correct.
Therefore, the linear function that has the same y-intercept as the given graph is the equation y = -2x + 10, corresponding to option 3.
for such more question on linear function
https://brainly.com/question/9753782
#SPJ8
Please help I’m stuck and keep getting the wrong answer

Answers
The time spent higher than 26 meters above the ground is 0.42 minutes. Answer: 0.42
A Ferris wheel is 30 meters in diameter and boarded from a platform that is 4 meters above the ground.
The six o'clock position on the Ferris wheel is level with the loading platform.
The wheel completes 1 full revolution in 2 minutes.
We have to find how many minutes of the ride are spent higher than 26 meters above the ground.
So, let's start with some given data,Consider the height of a person at the six o'clock position = 4 meters
So, the height of a person at the highest point = 4 + 15 = 19 meters (since the diameter is 30 meters, the radius will be 15 meters)
Also, the height of a person at the lowest point = 4 - 15 = -11 meters
Therefore, the Ferris wheel completes one cycle from the lowest point to the highest point and back to the lowest point.
So, the total distance travelled will be = 19 + 11 = 30 meters.
Also, we are given that the wheel completes 1 full revolution in 2 minutes.
We need to calculate the time spent higher than 26 meters above the ground.
So, the angle between the 6 o'clock position and 2 o'clock position will be equal to the angle between the 6 o'clock position and the highest point.
This angle can be calculated as follows:
Angle = Distance travelled by the Ferris wheel / Circumference of the Ferris wheel * 360 degrees
Angle = 30 / (pi * 30) * 360 degrees
Angle = 360 degrees / pi
= 114.59 degrees
So, the total angle between the 6 o'clock position and the highest point is 114.59 degrees.
Now, we need to find out how much time is spent at an angle greater than 114.59 degrees.
This can be calculated as follows:
Time = (Angle greater than 114.59 degrees / Total angle of the Ferris wheel) * Total time taken
Time = (180 - 114.59) / 360 * 2 minutes
Time = 0.42 minutes
For more related questions on time spent:
https://brainly.com/question/28263820
#SPJ8
How many square feet of outdoor carpet will we need for this hole?

Answers
The number of square feet needed to cover the hole is 44ft²
How many square feet of outdoor carpet will we need for this hole?To find this, we need to find the area of the green region and subtract the little square that it has inside.
Remember that for a rectangle, the area is the product between the dimensions, then the area of the green region is:
A = 12ft*4ft = 48ft²
The little square has an area:
a = 2ft*2ft = 4ft²
Then the area needed is:
area = 48ft² - 4ft² = 44ft²
Learn more about area at:
https://brainly.com/question/24487155
#SPJ1
Given f(x)= 4x^2 - 4 + 1 and g(x)= 2x-1, which of the following are expression(s) for f•g? Select all that apply.

Answers
The value for the expression, (f * g)(x) is calculated as: C. 8x³ - 12x² - 6x -1
How to Evaluate the Expressions of Functions?
We are given the following functions,
f(x) = 4x² – 4x + 1 and g(x) = 2x – 1.
To find the value of the expression, (f * g)(x), it means we have to multiply the functions together. See the steps explained below.
(f * g)(x) = f(x) * g(x)
Plug in the values:
(f * g)(x) = f(x) * g(x) = (4x² – 4x + 1)(2x – 1)
(f * g)(x) = 4x²(2x – 1) - 4x(2x – 1) + 1(2x – 1)
Apply the distribution property of equality:
(f * g)(x) = 8x³ – 4x² - 8x² + 4x + 2x – 1
Combine like terms:
(f * g)(x) = 8x³ - 12x² - 6x - 1
Therefore, the answer is: C. 8x³ - 12x² - 6x - 1.
To Learn more about evaluating functions from the given link.
brainly.com/question/2284360
#SPJ1
What is the exponential regression equation for the data set?
yˆ=1.08⋅32.11x
yˆ=(1.08⋅32.11)x
yˆ=32.11⋅0.08x
yˆ=32.11⋅1.08x

Answers
Answer:
yˆ=32.11⋅1.08x
Step-by-step explanation:
just took the test
Option: A is the correct answer.
The quadratic regression equation for the data set is:
A. y = 0.056x²+1.278x-0.886
What is equation?An equation is a mathematical statement that is made up of two expressions connected by an equal sign. In its simplest form in algebra, the definition of an equation is a mathematical statement that shows that two mathematical expressions are equal. For instance, 3x + 5 = 14 is an equation, in which 3x + 5 and 14 are two expressions separated by an 'equal' sign.
here, we have,
We are given a set of data value as:
x y
3 3.45
5 6.9
6 8.79
8 12.91
10 17.48
12 22.49
15 30.85
On plotting these points on a scatter plot we see that the line that best fits these data points is a parabola i.e. the equation is a equation of a quadratic function.
The equation of the line of best fit is:
y = 0.056x²+1.278x-0.886
To learn more on equation click:
brainly.com/question/24169758
#SPJ3
6/10 drivers look at their phone while driving. 3/10 drivers are having a conversation and look at their phone while driving. What is the probability that a driver is having a conversation while driving?
Answers
0.5 is the probability that a driver is having a conversation while driving.
What is probability?Probability is a number that expresses the likelihood or chance that a specific event will take place. Both proportions ranging from 0 to 1 and percentages ranging from 0% to 100% can be used to describe probabilities.
Given, 6/10 drivers look at their phones while driving. 3/10 drivers are having a conversation and looking at their phones while driving.
Let P(A) be the probability of drivers looking at their phones while driving.
and P(B) be the probability of drivers looking at their phones while driving.
Since:
P(A) = 0.6
P(A ∩ B) = 0.3
P(B) = (P(A ∩ B))/ P(A)
P(B) = 0.3/0.6
P(B) = 1/2
therefore, the probability that a driver is having a conversation while driving is 0.5.
Learn more about probability here:
https://brainly.com/question/30034780
#SPJ1
2. Explain how to calculate 8% of 350 by first calculating 1% of 350.
Answers
Answer:
28
Step-by-step explanation:
So 1% of 350 would be 3.5 because 350 divided by 100 is 3.5. You then get 3.5 and multiply it 8 times, which would be 28. (You multiply it 8 times because 8% is 8 times 1%.)
Answer:
this is hard i think its is 28
Step-by-step explanation:
because i put 128 and got it correct
Use the given dimensions to nd the areas of the vehicle and chairs. Then determine if the vehicle
could be used to haul both chairs in a single trip.
Answers
The 5 ft by 8 ft dimensions of the car and the (width) 2 ft by (height) 3 ft dimensions of the chair, indicates that the vehicle can haul both chairs in one trip.
What are the dimensions of a rectangularly shaped solid?The dimensions of rectangularly shaped solid are the height, the width and the length of the solid.
The possible dimensions of the vehicle and the chair obtained from a similar online question are;
Length of the vehicle = 8 feet
Width of the vehicle = 5 feet
The height of one chair = 3 feet
The width of one chair = 2 feet
Therefore;
The width of the vehicle of 5 feet indicates that the vehicle can contain the two chairs placed side by side with their widths of 2 feet each, to get;
Width of the two chairs = 2 feet + 2 feet = 4 feet < 5 feet
The two chairs placed horizontally, such that we get;
The total length of the horizontally placed chairs = 3 feet + 3 feet = 6 feet
The combined height of the two chaires, of 6 feet is less than the length of the car which is 8 feet, therefore;
The car can haul both chairs placed horizontally in a single trip.
The vehicle could therefore be used to haul both chairs in a single trip.
Learn more on the dimensions of regular solids here: https://brainly.com/question/29014642
#SPJ1
Help w this question please its #11 btw

Answers
Answer:
cgtcdtxcgv gg ok
Step-by-step explanation:
What is the y-intercept of the line representing Beatrice's monthly music subscription bill as a function of the number of songs she downloaded?
$$
Answers
The y-intercept of the line representing Beatrice's monthly music is 20
How to determine the y-intercept of the lineFrom the question, we have the following parameters that can be used in our computation:
y = -.95x + 20
To calculate the y-intercept of the line, we set x = 0
So, we have
y = -.95 * 0 + 20
Evaluate
y = 20
Hence, the y-intercept of the line representing Beatrice's monthly music is 20
Read more about intercept at
https://brainly.com/question/24363347
#SPJ9
Question
What is the y-intercept of the line representing Beatrice's monthly music subscription bill as a function of the number of songs she downloaded?
The equation is y = -.95x + 20
What is the volume to a rectangular prism when it has 9.3cm, 4cm and 4 cm
Answers
Given Dimension :-
9.3 cm , 4cm , 4cmTo find :-
The volume of rectangular prismSolution :-
Volume of rectangular prism=L × W × HVolume :- 9.3 × 4 × 4 cm³
Volume = 148.8 cm³
Answer:
Volume of rectangular prism is 148.8 cm³Step-by-step explanation:
In the question we have .
Length of prism = 9.3 cmWidth of prism = 4 cmHeight of prism = 4 cmAnd we are asked to find the volume of rectangular prism . We know that ,
\( \quad \pink{ \boxed{ \sf{Volume _{ (Rectangular\: Prism) } = L × W × H }}}\)
Where ,
L = Length of rectangular prismW = Width of rectangular prismH = Height of rectangular prismSolution : -
\( \quad \: \longmapsto \: 9.3 \times 4 \times 4\)
Calculating further :
\( \quad \: \longmapsto \:9.3 \times 16\)
We get :
\( \quad \: \longmapsto \: \purple{ \underline{\boxed{\frak{148.8 \: cm {}^{3} }}}}\)
Therefore , volume of rectangular Prism is 148.8 cm³#Keep Learningplease help with all questions (no links)

Answers
4) 223.4
5) 60.75
=
15. Given a rectangle ABCD with AD 12. The diagonals AC and BD intersect at point O such that
mZDOC = 30°. Find the area of the rectangle.
Answers
Answer:
To find the area, we need to find the side length AB (and DC).
The easiest way to approach this is to draw a sketch with all the given information (see attached).
As point O is the center point of the rectangle, we can draw a horizontal line from point O to the center point of BC (point M on the diagram) and create a right triangle. We can then use the Sine rule to find the shortest leg of the triangle (marked as x on the diagram). This will be half of the side length AB, and so to find the side length, simply multiply it by 2.
To find the missing angles of the right triangle:
m∠COM = (180° - 30°) ÷ 2 = 75°
m∠OCM = 180° - 90° - m∠COM = 90° - 75° = 15°
Sine rule
\(\sf \dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinB}\)
(where A, B and C are the angles and a, b and c are the sides opposite the angles)
\(\implies \dfrac{x}{\sin(15)}=\dfrac{6}{\sin(75)}\)
\(\implies x=\sin(15)\cdot \dfrac{6}{\sin(75)}\)
\(\implies x=12-6\sqrt{3}\)
As AB = \(2x\)
\(\begin{aligned} \implies AB & =2x\\ & =2(12-6\sqrt{3})\\ & =24-12\sqrt{3}\end{aligned}\)
Now we have both side lengths of the rectangle, we can easily calculate the area.
Area of a rectangle = width × length
= (24 - 12√3) × 12
= 288 - 144√3
= 38.5846837...
= 38.585 units² (nearest thousandth)

Evaluate this expression 2 (11 - 3) + 17
A. 31
B. 33
C. 35
D. 36
E. 45
Answers
Answer:
33
Step-by-step explanation:
22-6+17=33
this is correct i think
write the following in the form a+bi (2+5) - (-6 +bi)
Answers
The complex expression (2+5) - (-6 +bi) in the form a + bi is 13 - bi
How to evaluate the expression?The expression is given as
(2+5) - (-6 +bi)
The above expression is a complex expression
So, we have the following expression
(2+5) - (-6 +bi)
Remove the brackets in the above expression
So, we have the following expression
(2+5) - (-6 +bi) = 2 + 5 + 6 - bi
Evaluate the like terms in the above equation
So, we have the following expression
(2+5) - (-6 +bi) = 13 - bi
Hence, the solution to the complex expression is 13 - bi
Read more about complex expression at
https://brainly.com/question/11245197
#SPJ1
x is divided by -2 less than 5
Answers
Answer:
X/-2>5
Step-by-step explanation:
This is an Inequality
Mofor has homework assignments in five subjects. He only has time to do two of
them.
Answers
The decision of which two homework assignments to complete depends on Mofor's individual circumstances and priorities.
If Mofor only has time to do two homework assignments out of the five subjects, he will need to choose which subjects to prioritize. The specific subjects he chooses to work on will depend on various factors such as his strengths, weaknesses, upcoming deadlines, and personal preferences. Here are a few strategies he could consider:
1. Prioritize based on importance: Mofor can prioritize the homework assignments that carry more weight in terms of grades or have upcoming deadlines. This way, he ensures that he completes the assignments that have a higher impact on his overall academic performance.
2. Focus on challenging subjects: If Mofor finds certain subjects more difficult or time-consuming, he can prioritize those assignments to allocate more time and effort to them. This approach allows him to concentrate on improving his understanding and performance in subjects that require extra attention.
3. Balance workload: Mofor can choose to distribute his efforts evenly across subjects, selecting two assignments from different subjects. This strategy ensures that he maintains a balanced workload and avoids neglecting any particular subject.
The decision of which two homework assignments to complete depends on Mofor's individual circumstances and priorities. It is essential for him to consider his academic goals, time constraints, and personal strengths to make an informed decision.
For more such questions on homework
https://brainly.com/question/28521601
#SPJ8
Analyze the key features of the graph of f(x) shown below.
Use rules of transformations and the parent function to formulate an equation for the rational function shown in the graph. Show all your work.

Answers
Answer:
y = -2+1/3x
Step-by-step explanation:
Slope = -2
x - intercept = -3
To make the x-intercept positive you make it 1/3.
y = -2 +1/3x
Find the tangent line and the normal line to the curve at the given point.

Answers
The equation of the normal line to the curve x^2y^2 = 4 at the point (-1,-2) is y = x - 1.
To find the tangent line and normal line to the curve x^2y^2 = 4 at the point (-1,-2), we need to determine the derivative of the curve equation with respect to x and evaluate it at the given point.
First, let's differentiate the equation x^2y^2 = 4 implicitly with respect to x using the chain rule:
2x * (y^2) + 2y * (2xy * dy/dx) = 0
Simplifying the equation, we have:
2xy^2 + 4xy(dy/dx) = 0
Now, let's find the value of dy/dx at the point (-1,-2). Substitute x = -1 and y = -2 into the equation:
2*(-1)(-2)^2 + 4(-1)*(-2)(dy/dx) = 0
Simplifying further:
8 + 8(dy/dx) = 0
8(dy/dx) = -8
dy/dx = -1
We have found the derivative dy/dx at the point (-1,-2), which is -1. This represents the slope of the tangent line to the curve at that point.
Using the point-slope form of a line, we can write the equation of the tangent line as:
y - y₁ = m(x - x₁)
Substituting the values of (-1,-2) and dy/dx = -1 into the equation, we have:
y - (-2) = -1(x - (-1))
y + 2 = -1(x + 1)
y + 2 = -x - 1
y = -x - 3
Therefore, the equation of the tangent line to the curve x^2y^2 = 4 at the point (-1,-2) is y = -x - 3.
To find the normal line, we know that the slope of the normal line is the negative reciprocal of the slope of the tangent line. Therefore, the slope of the normal line is 1.
Using the point-slope form of a line again, we can write the equation of the normal line as:
y - y₁ = m'(x - x₁)
Substituting the values of (-1,-2) and m' = 1 into the equation, we have:
y - (-2) = 1(x - (-1))
y + 2 = x + 1
y = x - 1
for such more question on normal line
https://brainly.com/question/27877215
#SPJ8
