Answers
Answer:
Length(L) = y
perimeter of square = 4L
since L = y
so perimeter of square is 4y
Related Questions
Please help me !! would appreciate

Answers
The answers that describe the quadrilateral DEFG area rectangle and parallelogram.
The correct answer choice is option A and B.
What is a quadrilateral?A quadrilateral is a parallelogram, which has opposite sides that are congruent and parallel.
Quadrilateral DEFG
if line DE || FG,
line EF // GD,
DF = EG and
diagonals DF and EG are perpendicular,
then, the quadrilateral is a parallelogram
Hence, the quadrilateral DEFG is a rectangle and parallelogram.
Read more on quadrilaterals:
https://brainly.com/question/23935806
#SPJ1
brainliest, multiple choice, and 100 points! i really appreciate the help, and please let me know if you need help on anything, thanks!!

Answers
Answer:
C) ΔFHG ≅ ΔPRQ by the AAS triangle congruence theorem----------------------
AAS congruence theorem states that:
If two angles and a non-included side of one triangle are congruent to two angles and a non-included side of another triangle, then the triangles are congruent.We can see two angles and the non-included side are marked as congruent:
∠R ≅ ∠H, ∠Q ≅ ∠G and PQ ≅ FG,Hence the triangles are congruent:
ΔFHG ≅ ΔPRQTherefore the correct choice is C.
A box is to be made out of a 10 cm by 20 cm piece of cardboard. Squares of side length cm will be cut out of each corner, and then the ends and sides will be folded up to form a box with an open top. (a) Express the volume V of the box as a function of x. V = cm^3 (b) Give the domain of V in interval notation. (Use the fact that length and volume must be positive.) = ? (c) Find the length L , width W, and height H of the resulting box that maximizes the volume. (Assume that W < or = to L ) L= ?cm W= ?cm H= ? cm (d) The maximum volume of the box is ? cm^3.
Answers
(a) The volume V of the box as a function of x is V = 4x^3-60x^2+200x
(b) The domain of V in interval notation is 0<x<5,
(c) The length L , width W, and height H of the resulting box that maximizes the volume is H = 2.113, W = 5.773, L= 15.773
(d) The maximum volume of the box is 192.421 cm^2.
In the given question,
A box is to be made out of a 10 cm by 20 cm piece of cardboard. Squares of side length cm will be cut out of each corner, and then the ends and sides will be folded up to form a box with an open top.
(a) We have to express the volume V of the box as a function of x.
If we cut out the squares, we'll have a length and width of 10-2x, 20-2x respectively and height of x.
So V = x(10-2x) (20-2x)
V = x(10(20-2x)-2x(20-2x))
V = x(200-20x-40x+4x^2)
V = x ( 200 - 60 x + 4x^2)
V = 4x^3-60x^2+200x
(b) Now we have to give the domain of V in interval notation.
Since the lengths must all be positive,
10-2x > 0 ≥ x < 5 and x> 0
So 0 < x < 5
(c) Now we have to find the length L , width W, and height H of the resulting box that maximizes the volume.
We take the derivative of V:
V'(x) = 12x^2-120x+200
Taking V'(x)=0
0 = 4 (3x^2-30x+50)
3x^2-30x+50=0
Now using the quadratic formula:
x=\(\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)
From the equationl a=3, b=-30, c=50
Putting the value
x=\(\frac{30\pm\sqrt{(-30)^2-4\times3\times50}}{2\times3}\)
x= \(\frac{30\pm\sqrt{900-600}}{6}\)
x= \(\frac{30\pm\sqrt{300}}{6}\)
x= \(\frac{30\pm17.321}{6}\)
Since x<5,
So x= \(\frac{30-17.321}{6}\)
x= 2.113
So H = 2.113, W = 5.773, L= 15.773.
d) Now we have to find the maximum volume of the box.
V = HWL
V= 2.113*5.773*15.773
V = 192.421 cm^3
To learn more about volume of rectangle link is here
brainly.com/question/13798973
#SPJ4
6.4 x 1.2 show your work please and also 3.5 x 4.9 show your work please (will give brainlist thingy)
Answers
Answer:
6.4 x 1.2=7.68
Step-by-step explanation:
6.4
1.2
----
028
740
add
7.68
3.5 x 4.9=15.435
High-powered experimental engines are being developed by the Hendrix Motor Company for use in their new sports coupe. The engineers have calculated the maximum horsepower for the engines to be 630HP. Sixteen engines are randomly selected for testing. Perform a hypothesis test to determine whether the data suggests that the average maximum horsepower for the experimental engine is significantly different than the maximum horsepower calculated by the engineers. Assume the data are normally distributed and use a significance level of 0.05. Maximum Horsepower (HP) 643 641 598 621 644 601 649 652
671 653 666 654 670 670 666 654 Compute the value of the test statistic.
Answers
Sixteen randomly selected engines were tested, and their maximum horsepower values are provided. Assuming the data is normally distributed and using a significance level of 0.05, the test statistic is computed to assess the hypothesis.
To perform the hypothesis test, we will use a t-test for the mean. The null hypothesis (H0) assumes that the average maximum horsepower for the experimental engines is equal to the calculated maximum horsepower of 630HP. The alternative hypothesis (Ha) assumes that the average maximum horsepower is significantly different from 630HP.
Using the provided data, we calculate the sample mean of the maximum horsepower values:
(643 + 641 + 598 + 621 + 644 + 601 + 649 + 652 + 671 + 653 + 666 + 654 + 670 + 670 + 666 + 654) / 16 = 651.0625
Next, we calculate the sample standard deviation to estimate the population standard deviation:
s = √[((643 - 651.0625)^2 + (641 - 651.0625)^2 + ... + (654 - 651.0625)^2) / (16 - 1)] ≈ 24.663
Using the formula for the t-test statistic:
t = (sample mean - hypothesized mean) / (sample standard deviation / √sample size)
t = (651.0625 - 630) / (24.663 / √16) ≈ 2.027
Finally, comparing the calculated t-value of 2.027 with the critical t-value at a significance level of 0.05 (using a t-distribution table or software), we determine whether to reject or fail to reject the null hypothesis. If the calculated t-value falls outside the critical region, we reject the null hypothesis and conclude that there is a significant difference between the average maximum horsepower and the calculated maximum horsepower.
know more about hypothesis :brainly.com/question/23056080
#SPJ11
What is the slope of the line that passes through the pair of points?
(5, 8), (9,-3)
Answers
Answer:
-11/4
Step-by-step explanation:
slope = \(\frac{-3-8}{9-5} =\frac{-11}{4}\)
Hope this helps
Answer:
-11/4
Step-by-step explanation:
slope = (difference in y)/(difference in x)
slope = (-3 - 8)/(9 - 5) = -11/4
Help me please i dont get how to do it

Answers
The linear graph of y = 2x + 3 is shown below.
How to Draw the Graph of a Linear Equation?To graph the linear equation, plot each points from the table of values on a coordinate plane then connect the points to each other as a straight line.
Given the table, to fill it, substitute each value of x into y = 2x + 3:
For x = -2:
y = 2(-2) + 3
y = -4 + 3
y = -1
For x = -1:
y = 2(-1) + 3
y = -2 + 3
y = 1
For x = 0:
y = 2(0) + 3
y = 3
Thus, plot the points, (-2, -1), (-1, 1), (0, 3), (1, 5), and (2, 7) on a graph. The graph is shown below.
Learn more about linear graph on:
https://brainly.com/question/19040584
#SPJ1

Can you do 11 12 and 13 ignore 10

Answers
Answer:
I already done this thank you

A glide reflection is a composition of a line reflection and a translation that is parallel to the line of reflection. Unlike some composition of transformations, a glide reflection IS ____________________. Therefore, the line reflection and translation can be done in any ____________.
Answers
Answer:
" a glide reflection IS commutative. Therefore, the line reflection and translation can be done in any order."
Step-by-step explanation:
Transformations can be written as operators that act on functions or shapes.
For example, we can define the horizontal translation operator as:
T(k)
And if we apply this to a function, we get:
T(k)[ f(x) ] = f(x - k)
Now, the operators are not necessarily commutative.
This means that if we have two operators:
K and L
is not the same:
K[ L[ f(x) ]]
than:
L[ K[ f(x) ]]
An example of this can be a reflection across the y-axis and a horizontal translation, that composition is non-commutative.
Now, let's go to our case.
A glide reflection is commutative, so we can perform the transformations in any order, then the statement is:
" a glide reflection IS commutative. Therefore, the line reflection and translation can be done in any order."
How to convert polar coordinates to rectangular coordinates.
Answers
the rectangular coordinates corresponding to the polar coordinates (5, π/6) are approximately (4.33, 2.5).
To convert polar coordinates to rectangular coordinates, you can use the following formulas:
Given polar coordinates (r, θ), where r represents the distance from the origin (or pole) to the point, and θ represents the angle between the positive x-axis and the line connecting the origin to the point:
Rectangular coordinate x = r * cos(θ)
Rectangular coordinate y = r * sin(θ)
Here's a step-by-step process for converting polar coordinates to rectangular coordinates:
1. Identify the given polar coordinates (r, θ).
2. Use the formula x = r * cos(θ) to calculate the rectangular coordinate x.
3. Use the formula y = r * sin(θ) to calculate the rectangular coordinate y.
4. The rectangular coordinates (x, y) represent the equivalent representation of the given polar coordinates.
For example, let's say we have polar coordinates (r, θ) = (5, π/6). To convert these to rectangular coordinates:
x = 5 * cos(π/6) = 5 * (√3/2) = 5√3/2 ≈ 4.33
y = 5 * sin(π/6) = 5 * (1/2) = 5/2 = 2.5
So, the rectangular coordinates corresponding to the polar coordinates (5, π/6) are approximately (4.33, 2.5).
to know more about polar visit:
brainly.com/question/27627764
#SPJ11
define a simulation by telling how you represent correct answers, incorrect answers, and the quiz. Use your simulation to find each experimental probability.
If you guess the answers at random, what is the probability of getting at least three correct answers on a five-question true-or-false quiz?
Answers
In this simulation, we will represent correct answers as "C" and incorrect answers as "I." The quiz will consist of five true-or-false questions. To find the experimental probability of getting at least three correct answers,
we will repeat the quiz multiple times and keep track of the number of times we obtain three or more correct answers. The experimental probability is then calculated by dividing the number of successful outcomes by the total number of trials.
Running the simulation for a large number of trials, let's say 10,000, we will randomly guess the answers for each question. For each trial, we count the number of correct answers. If the count is three or greater, we consider it a successful outcome.
After running the simulation with 10,000 trials, we record the number of successful outcomes and divide it by the total number of trials. This provides us with the experimental probability of getting at least three correct answers on the quiz when guessing randomly.
By calculating the experimental probability through simulation, we can estimate the likelihood of obtaining three or more correct answers on a five-question true-or-false quiz when guessing randomly.
Learn more about Simulation here:
brainly.com/question/32099547
#SPJ11
Tameca already has $55
dollars in her savings account. If
she puts $5 per week in her
account, write and solve an inequality
inequality to find out how man
weeks she must save to have a
least $100 in her account.
Answers
Answer:
5x+55=100
Step-by-step explanation:
What information is in the text but not in the graph?

Answers
Answer:
B. More money was given than expected in 1994
Step-by-step explanation:
Nowhere is it mentioned what amount was expected as donations. Only actual amounts received are shown on the graph
Hence this is an assumption and not necessarily fact
PLEASE HELPPPPPP TYSMMMM
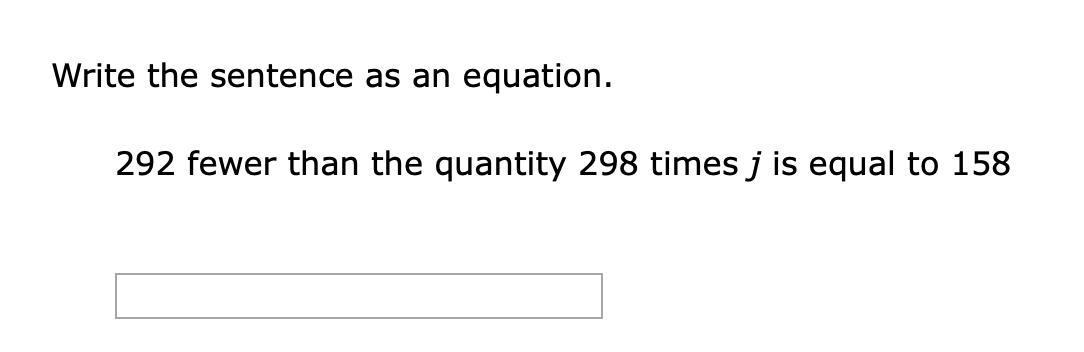
Answers
Answer:
292<298xj=158
Hope this helps!
Solve the following linear programming problem by applying the simplex method to the dual problem. Minimize
Minimize
subject to
x
1
,x
2
≥0
C=4x
1
+23x
2
5x
1
+x
2
≥2
x
1
+5x
2
≥2
Select the correct choice below and fill in any answer boxes present in your choice. A. MinC= at x
1
=,x
2
= B. There is no minimum value of C.
Answers
A. MinC= at x1 = 0, x2 = 0
The correct choice is A, which means the minimum value of C occurs at x1 = 0 and x2 = 0. This implies that the objective function C is minimized when both decision variables x1 and x2 are set to zero.
To solve the linear programming problem using the simplex method, we first convert the minimization problem into a maximization problem. We introduce slack variables s1 and s2 to convert the inequalities into equalities. The problem becomes:
Maximize Z = -4x1 - 23x2
subject to:
5x1 + x2 + s1 = 2
x1 + 5x2 + s2 = 2
x1, x2, s1, s2 ≥ 0
We then set up the initial simplex tableau and apply the simplex method to find the optimal solution. Since the question does not provide the initial tableau or any intermediate steps, it is not possible to determine the values for x1 and x2 that result in the minimum value of C. Therefore, the correct choice is that there is no minimum value of C based on the given information.
The simplex method is an iterative algorithm that starts with an initial feasible solution and improves it iteratively until an optimal solution is reached. In each iteration, the algorithm selects a pivot element to perform row operations and improve the objective function value. The process continues until no further improvement is possible, indicating the optimal solution. However, without the intermediate steps or the final simplex tableau, we cannot determine the values of x1 and x2 that minimize C. Hence, the answer is that there is no minimum value of C provided by the given information.
Learn more about function here : brainly.com/question/30721594
#SPJ11
10) Determine whether the events of rolling a fair die two times are disjoint, independent, both, or neither. A) Disjoint. B) Exclusive. C) Independent. D) All of these. E) None of these.
Answers
The answer is option (C), that is, the events of rolling a fair die two times are independent. The events are neither disjoint nor exclusive.
When rolling a fair die two times, one can get any one of the 36 possible outcomes equally likely. Let A be the event of obtaining an even number on the first roll and let B be the event of getting a number greater than 3 on the second roll. Let’s see how the outcomes of A and B are related:
There are three even numbers on the die, i.e. A={2, 4, 6}. There are four numbers greater than 3 on the die, i.e. B={4, 5, 6}. So the intersection of A and B is the set {4, 6}, which is not empty. Thus, the events A and B are not disjoint. So option (A) is incorrect.
There is only one outcome that belongs to both A and B, i.e. the outcome of 6. Since there are 36 equally likely outcomes, the probability of the outcome 6 is 1/36. Now, if we know that the outcome of the first roll is an even number, does it affect the probability of getting a number greater than 3 on the second roll? Clearly not, since A∩B = {4, 6} and P(B|A) = P(A∩B)/P(A) = (2/36)/(18/36) = 1/9 = P(B). So the events A and B are independent. Thus, option (C) is correct. Neither option (A) nor option (C) can be correct, so we can eliminate options (D) and (E).
To learn more about probability, refer:-
https://brainly.com/question/31828911
#SPJ11
A mass of m= } kg is attached to a spring with a spring constant of k = 50 N/m. If the mass is set in motion with an initial position of x(0) = 1 m and an initial velocity of x'(0) = -3 m/sec. Determine the frequency, period and amplitude of the motion. (8 Pts)
Answers
The amplitude of the motion is a = 1/10.now that we have the angular frequency ω = 10 rad/s and the amplitude a = 1/10, we can determine the frequency and period of the motion:
frequency (f) is the number of cycles per unit of time, given by f = ω / (2π):
f = 10 / (2π) ≈ 1.
to determine the frequency, period, and amplitude of the motion of the mass attached to the spring, we can use the equation for simple harmonic motion:
x(t) = a * cos(ωt + φ)
where:
- x(t) is the displacement of the mass at time t
- a is the amplitude of the motion
- ω is the angular frequency
- φ is the phase angle
the angular frequency is given by ω = sqrt(k/m), where k is the spring constant and m is the mass.
given:
k = 50 n/m
m = 0.5 kg
ω = sqrt(50/0.5) = sqrt(100) = 10 rad/s
to find the amplitude, we need to find the maximum displacement of the mass from its equilibrium position. this can be determined using the initial position and velocity.
given:
x(0) = 1 m (initial position)
x'(0) = -3 m/s (initial velocity)
the general equation for displacement as a function of time is:
x(t) = a * cos(ωt + φ)
differentiating the equation with respect to time gives the velocity function:
x'(t) = -a * ω * sin(ωt + φ)
we can plug in the initial conditions to solve for a:
x(0) = a * cos(0 + φ) = 1
a * cos(φ) = 1
x'(0) = -a * ω * sin(0 + φ) = -3
-a * ω * sin(φ) = -3
dividing the second equation by the first equation:
[-a * ω * sin(φ)] / [a * cos(φ)] = -3 / 1
-ω * tan(φ) = -3
simplifying, we have:
tan(φ) = 3/ω = 3/10
using the trigonometric identity tan(φ) = sin(φ) / cos(φ), we can express sin(φ) and cos(φ) in terms of a common factor:
sin(φ) = 3, cos(φ) = 10
substituting the values of sin(φ) and cos(φ) into the equation x(0) = a * cos(φ), we can solve for a:
a * cos(φ) = 1
a * 10 = 1
a = 1/10 59 hz
period (t) is the time taken to complete one cycle, given by t = 1 / f:
t = 1 / 1.59 ≈ 0.63 s
Learn more about angle here:
https://brainly.com/question/31818999
#SPJ11
6m+10p when m=8 and p=14
Answers
Answer:
184
Step-by-step explanation:
6m + 10p
6(8) + 10(14) =
48 + 140 = 184
plz give brainliest :)
What is the volume, in cubic centimeters, of a right square pyramid
with base edges that are 64 cm long and a slant height of 40 cm
Answers
The volume of the right squared pyramid with the given base edges and slant height is 32768 cubic centimeters.
What is the volume of right square pyramid?The volume of a square pyramid is expressed as;
V = (1/3)a²h
Where a is the base length and h is the height of the pyramid
Given that;
Base edges of the square base a = 64cmSlant height s = 40cmHeight of the pyramid h = ?Volume = ?First, we determine the height of the pyramid using Pythagorean theorem.
c² = a² + b²
c = s = 40cma = half of the base length = a/2 = 64cm/2 = 32cmb = h(40cm) = (32cm)² + h²
1600cm² = 1024cm² + h²
h² = 1600cm² - 1024cm²
h² = 576cm²
h = √576cm²
h = 24cm
Now, we calculate the volume of the right square pyramid;
V = (1/3)a²h
V = (1/3) × (64cm)² × 24cm
V = (1/3) × 409664cm² × 24cm
V = 32768cm³
Therefore, the volume of the right squared pyramid with the given base edges and slant height is 32768 cubic centimeters.
Learn more about volume of pyramids here: https://brainly.com/question/27666514
#SPJ1
Prove the identity a p(p−1) ≡ 1 (mod p 2 ), where a is coprime to p, and p is prime. (Hint: Try to mimic the proof of Fermat’s Little Theorem from the notes.)
Answers
To prove this identity, we start with Fermat's Little Theorem, which states that if p is a prime number and a is any integer coprime to p, then a^(p-1) ≡ 1 (mod p).
Using this theorem, we can rewrite the given identity as a^(p-1) * a(p-2) ≡ 1 (mod p^2).
Next, we can multiply both sides by a to get a^(p-1) * a(p-1) ≡ a (mod p^2).
Since a and p are coprime, we can use Euler's Totient Theorem, which states that a^φ(p) ≡ 1 (mod p) where φ(p) is the Euler totient function. Since p is prime, φ(p) = p-1, so a^(p-1) ≡ 1 (mod p).
Using this result, we can rewrite our identity as a^(p-1) * a(p-1) * a^-1 ≡ a^(p-1) ≡ 1 (mod p), which implies that a^(p-1) ≡ 1 (mod p^2).
Therefore, we have proven the identity a p(p−1) ≡ 1 (mod p 2 ), where a is coprime to p, and p is prime.
Visit here to learn more about Fermat's Little Theorem : https://brainly.com/question/30761350
#SPJ11
is 6km is not as far as 6 miles true or false
Answers
Answer:
False.
6 miles is farther than 6 kilometers. One mile is equal to 1.60934 kilometers, so 6 miles is equal to 6 x 1.60934 = 9.65604 kilometers. Therefore, 6 miles is farther than 6 kilometers.
Step-by-step explanation:
The answer is:
trueWork/explanation:
We can't really compare two things if they have different units.
So we need to convert kilometers to miles first.
1 km is approximately equal to 0.621 miles.
So 6 km would be approximately 3.728 miles.
6 miles is further away than 3.728 miles.
Hence, the answer is true.6 km is not as far as 6 miles. And now we know why.
The function in the table below shows the relationship between the total number of houses built in an area and the number of months that passed. A two column table with five rows. The first column, Months Passed, has the entries, 0, 3, 4, 8. The second column, Total Houses Built, has the entries 0, 33, 46, 108. Which best describes the data set? It is nonlinear because the “Total Houses Built” column does not increase at a constant additive rate. It is nonlinear because the “Months Passed” column does not increase at a constant additive rate. It is nonlinear because the increase in the “Total Houses Built” compared to the increase in the “Months Passed” does not show a constant rate of change. It is linear because the increase in the “Total Houses Built” compared to the increase in the “Months Passed” shows a constant rate of change
Answers
Answer:
I just did it this is the right answer.
It is nonlinear because the increase in the “Total Houses Built” compared to the increase in the “Months Passed” does not show a constant rate of change.
Step-by-step explanation:
The correct statement is,
'' It is nonlinear because the increase in the “Total Houses Built” compared to the increase in the “Months Passed” does not show a constant rate of change.''
What is Equation of line?The equation of line in point-slope form passing through the points
(x₁ , y₁) and (x₂, y₂) with slope m is defined as;
⇒ y - y₁ = m (x - x₁)
Where, m = (y₂ - y₁) / (x₂ - x₁)
Given that;
The first column, Months Passed, has the entries, 0, 3, 4, 8.
And, The second column, Total Houses Built, has the entries,
0, 33, 46, 108.
Hence, Rate of change are,
⇒ (33 - 0) / (3 - 0) = 11
⇒ (46 - 33) / (4 - 3) = 13
Thus, It does not show a constant rate of change.
Hence, The correct statement is,
'' It is nonlinear because the increase in the “Total Houses Built” compared to the increase in the “Months Passed” does not show a constant rate of change.''
Learn more about the equation of line visit:
https://brainly.com/question/18831322
#SPJ7
help me asap plss school is done in 4 mins plsssss help me asap


Answers
Answer:
3(y +8) (d+e) /4
Step-by-step explanation:
I gotta get to class too soon so my explanation here is just to get this sent. hopefully it does. I tried my best. could be wrong
Put a lid on it! The supplier is considering two changes to reduce to 1% the
percentage of its large-cup lids that are too small. One strategy is to adjust the
mean diameter of its lids. Another option is to alter the production process,
thereby decreasing the standard deviation of the lid diameters,
a. If the standard deviation remains at o = 0.02 inch, at what value should the
supplier set the mean diameter of its large-cup lids so that only 1% are too
small to fit?
b. If the mean diameter stays at = 3.98 inches, what value of the standard
deviation will result in only 1% of lids that are too small to fit?
c. Which of the two options in parts (a) and (b) do you think is preferable? Justify
your answer. (Be sure to consider the effect of these changes on the percent of
lids that are too large to fit.)
Answers
Answer:
A) 3.996 inches
B) 0.01
C) option B
Step-by-step explanation:
Note: The diameter of the lid is between : 3.95 and 4.05
A) calculate the supplier set mean diameter
std = 0.02 inch
P( x < 3.95 ) = 1% = 0.01
= P ( Z < \((\frac{3.95 - u }{0.02})\) ) = P ( Z < -2.3263 ) = 0.01
therefore :
\((\frac{3.95 - u }{0.02})\) = -2.3263
hence : u = 3.996 inches ( mean diameter )
B) At mean diameter = 3.98 calculate the value of std
P ( X < 3.95 ) = 0.01
= P ( Z < \(( \frac{3.95-3.98 }{std } )\) ) = P ( Z < -2.3263 ) = 0.01
therefore
\(( \frac{3.95-3.98 }{std } )\) = -2.3263
hence std = 0.01 inch
C) option B is preferable because its mean diameter is smaller and the percent of lids too large to fit is considered more carefully using option B
can somebody help me i dont know how to do this

Answers
Answer:
The line y = -2 - 4x has slope -4.
Slopes of perpendicular lines have product -1, so the slope of a line perpendicular to a line with slope -4 will be 1/4.
Slopes of parallel lines are the same, so the slope of a line parallel to a line with slope -4 will be -4.
Answer:
\(\frac{1}{4}\) and - 4
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
given
y = - 2 - 4x , or
y = - 4x - 2 ← in slope- intercept form
with slope m = - 4
given a line with slope m then the slope of a line perpendicular to it is
\(m_{perpendicular}\) = - \(\frac{1}{m}\) = - \(\frac{1}{-4}\) = \(\frac{1}{4}\)
slope of perpendicular line is \(\frac{1}{4}\)
• Parallel lines have equal slopes , then
slope of parallel line is - 4
2(4x-3)>-3(3x)+5x help
Answers
Answer:
\(x>1/2\)
Step-by-step explanation:
\(2(4x-3)>-3(3x)+5x\)
Expand the brackets.
\(8x-6>-9x+5x\)
Add -9x and 5x
\(8x-6>-4x\)
Add 4x and 6x on both sides.
\(8x+4x>6\)
Add the like terms.
\(12x>6\)
Divide 12 into both sides.
\(12x/12>6/12\)
\(x>1/2\)
Answer:
x > 1/2
Step-by-step explanation:
We have the inequality 2(4x - 3) > -3(3x) + 5x.
Let's first expand all the parentheses on the left side. When doing so, remember that we take the sum of the products of the outside number with each of the inside numbers:
2 * 4x + 2 * (-3) > -9x + 5x
8x - 6 > -4x
Add 4x and 6 to both sides:
8x + 4x > 6
12x > 6
Divide by 12:
x > 6/12
x > 1/2
Thus, any x value greater than 1/2 works: x > 1/2.
~ an aesthetics lover
PLEASE HELP URGENT PLEASE HELP PLEASE HELP PLS

Answers
Answer:
angle OPR and angle OPM
Step-by-step explanation:
it adds up to 180 degrees
5x-3(x-2)=4
This is for Algebra 1
Answers
Answer:
5x-3(x-2)=4
5x-3x+6=4
2x+6=4
2x= 4-6
2x= -2
x = -1
David is trying to solve the following. If 24 people have the flu out of 360 people, how many would have the flu out of 900? choose every proportion that david could use to solve this problem.
Answers
After choosing every proportion, if 24 people have the flu out of 360 people, then 60 people would have the flu out of 900.
We know very well that if any relation of one quantity is given with the second quantity at any instant of time and same relation question is asking at another instant of time, then always use unitary methods.
The unitary method is defined as a technique for solving a problem by first finding the value of a single unit, and then with the help of found value the necessary value can be find by multiplying the single unit value.
Here, In 360 people number of people would have flu=24
∴In 900 people number of people would have flu=(24×900)/360
=21600/360
=60people.
Hence, number of people would have flu is 60.
To know more about unitary methods, visit here:
https://brainly.com/question/28276953
#SPJ4
2. Estefan wanted to buy a stereo that was half-off the regular price of $150. How much was the stereo's sale price?
Answers
The Selling Price of the Stereo will be $75
What is Selling Price and Cost Price?Cost Price is defined as the amount that is paid to purchase an article or the price at which an article is made is known as its cost price. The cost price can be abbreviated as C.P.
Selling Price is defined as the price at which an article is sold to the customer. The selling price is abbreviated as S.P.
Profit and Loss can be estimated through Selling Price and Cost Price.
Profit =Selling Price-Cost Price ,only when the selling price is greater than the Cost price.
Loss= Cost Price- Selling price , only when the cost price is greater than the Selling price.
Step by step explanation
As we know that the Cost Price=$150
and Selling Price is 50% of Cost Price
∴Sale Price will be $75
To know more about Selling Price, Visit:
https://brainly.com/question/28017453
#SPJ9
