i just wanna say i hope your having a good day! and you are enough! keep going u got this!
Answers
aww,thank you ^^
i hope you're having a good day as well
Answer:
thank youuu
Step-by-step explanation:
Related Questions
find the bearing of the ship for the given values of x and y. round to the nearest tenth of degree. x=9.4 y=10.1
Answers
Using trigonometry we obtain the bearing of the ship ≈ 41.8 degrees.
To obtain the bearing of the ship given the values of x and y, we can use trigonometry.
The bearing represents the angle in degrees measured clockwise from the north direction.
First, we need to determine the angle θ between the positive x-axis and the line connecting the origin (0,0) and the point (x, y).
We can use the inverse tangent function (arctan) to find this angle:
θ = arctan(y/x)
Substituting the values x = 9.4 and y = 10.1 into the equation:
θ = arctan(10.1/9.4)
Using a calculator, we find that θ is approximately 48.2 degrees.
However, this angle corresponds to the angle counterclockwise from the positive x-axis.
To convert it to the bearing (measured clockwise from the north direction), we subtract this angle from 90 degrees:
Bearing = 90 - θ = 90 - 48.2 = 41.8 degrees.
To know more about trigonometry refer here:
https://brainly.com/question/12068045#
#SPJ11
gt the size of bass caught in strawberry lake is normally distributed with a mean of 11 inches and a standard deviation of 3 inches. suppose you catch 4 fish. what is the probability the average size of the fish you caught is more than 13 inches?
Answers
The probability that the average size of the fish you caught is more than 13 inches is approximately 0.0918
We can solve this problem by using the Central Limit Theorem, which states that the sample mean of a sufficiently large sample size will be normally distributed with a mean equal to the population mean and a standard deviation equal to the population standard deviation divided by the square root of the sample size.
In this case, we are given that the population mean is 11 inches and the population standard deviation is 3 inches. We are also given that we have a sample size of 4.
First, we need to calculate the standard error of the mean (SE) using the formula
SE = σ / sqrt(n)
where σ is the population standard deviation and n is the sample size.
SE = 3 / sqrt(4) = 1.5
Next, we need to standardize the sample mean using the formula
z = (x - μ) / SE
where x is the sample mean, μ is the population mean, and SE is the standard error of the mean.
z = (13 - 11) / 1.5 = 1.33
Finally, we can use a standard normal distribution table or calculator to find the probability that a standard normal variable is greater than 1.33. The probability is approximately 0.0918.
Learn more about probability here
brainly.com/question/11234923
#SPJ4
3. Where does solar energy come from?
Enter your answer
Answers
Answer: sun
Step-by-step explanation:
cause I said
Find the coordinates of the other endpoint of the segment, given its midpoint and one endpoint. (Hint: Let (x,y) be the unknown endpoint. Apply the midpoint formula,
and solve the two equations for x and y.)
midpoint (-1,14), endpoint (-4,12)
The other endpoint is 1
(Type an ordered pair.)
Answers
Answer:
(1,15)
Step-by-step explanation:
first, you look at the coordinates
then, you think how far are the 1st number away from the 2nd
finally, you'd get the answer of 15 there you have your answer
Which type of mathematical problem is too complex for a classical computer to solve efficiently?
Answers
Calculating the circumference of a circle based on the circle's diameter.
What kind of problems can a quantum computer solve?
Yet another difficult area that quantum computers cater to is that of solving difficult combinatorics problems. The algorithms within quantum computing aim at solving difficult combinatorics problems in graph theory, number theory, and statistics.10 Difficult Problems Quantum Computers can Solve Easily-
Quantum encryption. Simulation of quantum systems. ab initio calculations.Solving difficult combinatorics problems.Supply chain logistics. Optimization.Finance. Drug development.Learn more about quantum computer
brainly.com/question/15188300
#SPJ4
The complete question is -
Which type of mathematical problem is too complex for a classical computer to solve efficiently?
a. converting an irregular fraction to an approximate decimal value
b. multiplying two numbers that both have a large number of digits
c. finding two prime factors that result in a specific value when multiplied
d. calculating the circumference of a circle based on the circle's diameter
can I get help please
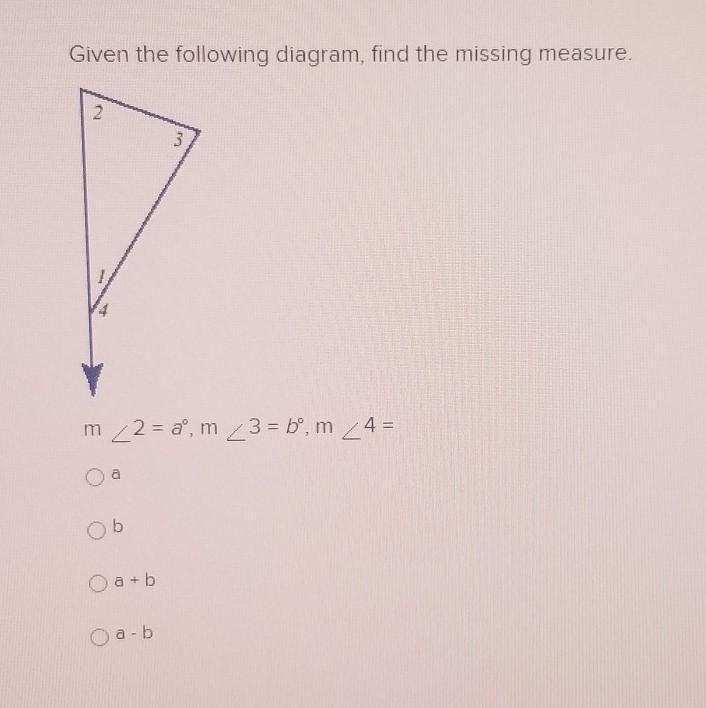
Answers
Answer:
a + b
Step-by-step explanation:
sum of two opposite interior angles are equal to one exterior
hope it helps
solve the linear equation 4x-(2x-1)=x+5+x-6
Answers
The linear equation doesn't have a solution.
How to compute the value?The linear equation given is illustrated as: 4x-(2x-1) = x+5+x-6
This will be solved thus:
4x - 2x + 1 = x+5+x-6
4x - 2x + 1 = 2x - 1.
2x + 1 = 2x - 1
Collect like terms
2x - 2x = -1 - 1
0 = -2
This illustrates that the equation doesn't have a solution.
Learn more about equations on:
brainly.com/question/28280501
#SPJ1
There are four students named A,B,C, and D. All four of them are loss averse over money, with the same value function for money: v(x dollars )={√x x ≥ 0
{-2√-x x < 0
All three of them are also loss averse over mugs, with the same value function for mugs:
v(y mugs)={3y y ≥ 0
{4y y < 0
Total utility is the sum of the gain/loss utility for mugs and the gain/loss utility for money. The reference point is the status quo, that is, a person's initial endowment. Student A owns a mug and is willing to sell it for a price of a dollars or more. Student B does not own a mug and is willing to pay up to b dollars for buying it. Student C does not own a mug and is indifferent between getting a mug and getting c dollars. Student D is indifferent between losing a mug and losing d dollars.
1. Solve for a,b,c, and d.
2. Instead, suppose A, B, C, and D are only loss averse over mugs, but not over money. That is, their value function for money is instead:
v(x dollars)={√x x ≥ 0
{-√-x x < 0
and their value function for mugs remains:
v(y mugs)={3y y ≥ 0
{4y y < 0
Solve for a,b,c, and d.
3. Instead, suppose A,B,C, and D are not loss averse:
v(x dollars)={√x x ≥ 0
{-√-x x < 0
and v(y mugs)=3y
Solve for a,b,c, and d.
4. Suppose A, B, C, and D are not loss averse (as in the previous question), but their value for a mug varies with ownership. Specifically, the value of the mug is 3 for someone who does not currently own the mug, and 4 for someone who currently owns a mug. Solve for a,b,c, and d.
Answers
As per the question, All four students A, B, C, and D are loss-averse over money and have the same value function as below:v(x dollars)={√x x ≥ 0 {-2√-x x < 0They are also loss averse over mugs and have the same value function.
v(y mugs)={3y y ≥ 0
{4y y < 0
Now, we have to find the values of a, b, c and d as below:
- Student A owns a mug and is willing to sell it for a price of a dollars or more. i.e v(a) = v(0) + v(a-A), where A is the initial endowment of A. According to the given function, v(0) = 0, v(a-A) = 3, and v(A) = 4.
So, a ≥ A+3/2
- Student B does not own a mug and is willing to pay up to b dollars for buying it. i.e v(B-b) = v(B) - v(0), where B is the initial endowment of B. According to the given function, v(0) = 0, v(B-b) = -4, and v(B) = -3.
So, b ≤ B+1/2
- Student C does not own a mug and is indifferent between getting a mug and getting c dollars. i.e v(c) = v(0) + v(c), where C is the initial endowment of C. According to the given function, v(0) = 0, v(c) = 3.
So, c = C/2
- Student D is indifferent between losing a mug and losing d dollars. i.e v(D-d) = v(D) - v(0), where D is the initial endowment of D. According to the given function, v(0) = 0, v(D-d) = -3.
So, d = D/2
2) In this case, value function for money changes to:v(x dollars)={√x x ≥ 0
{-√-x x < 0
However, the value function for mugs remains the same:v(y mugs)={3y y ≥ 0
{4y y < 0
Therefore, values for a, b, c, and d will remain the same as calculated in part (1).
3) In this case, students are not loss-averse. Value function for money:v(x dollars)={√x x ≥ 0
{-√-x x < 0
Value function for mugs:v(y mugs)={3y y ≥ 0
The reference point is the status quo, i.e initial endowment. So,
- Student A owns a mug and is willing to sell it for a price of a dollars or more. The value of mug for A is 3 initially and he would sell it for 3 or more.
So, a ≥ A+3/2
- Student B does not own a mug and is willing to pay up to b dollars for buying it. The value of mug for B is 3 initially and he would buy it for 3 or less.
So, b ≤ B+3/2
- Student C does not own a mug and is indifferent between getting a mug and getting c dollars. The value of the mug for C is 3 initially.
So, c = 3
- Student D is indifferent between losing a mug and losing d dollars. The value of the mug for D is 3 initially.
So, d = 3
4) In this case, value function for money:v(x dollars)={√x x ≥ 0
{-√-x x < 0
Value function for mugs: Mug will have a value of 4 for someone who owns it and 3 for someone who does not own it.
The reference point is the status quo, i.e initial endowment. So,
- Student A owns a mug and is willing to sell it for a price of a dollars or more. The value of mug for A is 4 initially and he would sell it for 4 or more.
So, a ≥ A+2
- Student B does not own a mug and is willing to pay up to b dollars for buying it. The value of mug for B is 3 initially and he would buy it for 3 or less.
So, b ≤ B+3/2
- Student C does not own a mug and is indifferent between getting a mug and getting c dollars. The value of the mug for C is 3 initially and he would like to buy it for 3.
So, c = 3
- Student D is indifferent between losing a mug and losing d dollars. The value of the mug for D is 3 initially.
So, d = 3.
To know more about students visit:
https://brainly.com/question/29101948
#SPJ11
Let X = the number of coin tosses won by the LA Rams during one season. What is the probability that they win the coin toss in exactly 10 of their 16 games?
Answers
The probability that they win the coin toss in exactly 10 of their 16 games.
What is the probability?
Probability is a mathematical concept that deals with the likelihood or chance of an event occurring. It is expressed as a number between 0 and 1, with 0 indicating that an event is impossible and 1 indicating that an event is certain to occur. The probability of an event A, denoted as P(A), is calculated as the number of favorable outcomes divided by the number of possible outcomes.
P(getting heads on one toss) = 1 / 2 because the coin is unbiased.
So P(getting all heads in 10 tosses).
= \((1/2)^{10}\)
= 1/ 1024
= .0009765
Hence, the probability that they win the coin toss in exactly 10 of their 16 games.
To learn more about probability refer to
https://brainly.com/question/24756209
#SPJ1
Consider two digital fuel pumps A and B that could be used in a single gas station. Pump A has a mean effective process time of 4 minutes with squared-coefficient of variation of 0.5. Pump B has a mean effective time of 3 minute with squared-coefficient of variation of 5. Assume that the arrival rate of cars is 0.2 car per minute with squared-coefficient of variation of 1. Which pump will have a longer average cycle time? (Hint: the number of machines, m, is 1.)
Answers
Therefore, Pump B will have a longer average cycle time compared to Pump A.
To determine which pump will have a longer average cycle time, we need to calculate the cycle time for each pump based on the given information and compare the results. The cycle time for a single-server system can be calculated using Little's Law: Cycle Time = (1 / Arrival Rate) * (1 / (1 - Utilization))
Given:
Arrival Rate = 0.2 car per minute
Squared-Coefficient of Variation (CV^2) for Arrival Rate = 1
Utilization can be calculated as the product of the mean effective process time and the arrival rate:
Utilization = Mean Effective Process Time * Arrival Rate
For Pump A:
Mean Effective Process Time (A) = 4 minutes
Squared-Coefficient of Variation for Pump A = 0.5
Utilization (A) = 4 * 0.2 = 0.8
For Pump B:
Mean Effective Process Time (B) = 3 minutes
Squared-Coefficient of Variation for Pump B = 5
Utilization (B) = 3 * 0.2 = 0.6
Now, let's calculate the cycle time for each pump:
Cycle Time (A) = (1 / 0.2) * (1 / (1 - 0.8))
= 5 minutes
Cycle Time (B) = (1 / 0.2) * (1 / (1 - 0.6))
= 2.5 minutes
To know more about Pump,
https://brainly.com/question/32143195
#SPJ11
A statistical analysis of 1,000 long-distance telephone calls made by a company indicates that the length of these calls is normally distributed, with a mean of 290 seconds and a standard deviation of 30 seconds. Complete parts (a) through (c).
a. What is the probability that a call lasted less than 230 seconds?
The probability that a call lasted less than
23 seconds is ?
(Round to four decimal places as needed.)
b. What is the probability that a call lasted between 230 and 330 seconds?
The probability that a call lasted between
230 and 330 seconds is
(Round to four decimal places as needed.)
c. What is the probability that a call lasted more than 330 seconds?
The probability that a call lasted more than
330 seconds is
(Round to four decimal places as needed.)
Answers
To find the probability of the call lasting less than 230 seconds, we have to find P(X<230). Here X follows normal distribution with mean = 290
The given data: Meanμ = 290 seconds
Standard deviation σ = 30 seconds
Sample size n = 1000a) and
standard deviation = 30.
We get the value of 0.0228, which represents the area left (or below) to z = -2. Therefore, the probability that the call lasted less than 230 seconds is 0.0228 (or 2.28%). By using z-score formula;
Z=(X-μ)/σ
Z=(230-290)/30
= -2P(X<230) is equivalent to P(Z < -2) From z-table,
0.6384 (or 63.84%) P(230330) is equivalent to 1 - P(X<330)Here X follows normal distribution with mean = 290 and standard deviation = 30.From part b,
We already have P(X<330).Therefore, P(X>330) = 1 - 0.9082 = 0.0918, which is equal to 9.18%. Therefore, the probability that the call lasted more than 330 seconds is 0.1356 (or 13.56%).Answer: 0.1356 (or 13.56%). In parts a, b, and c, the final probabilities are rounded off to four decimal places as needed, as per the instructions given. However, these values are derived from the exact probabilities and can be considered accurate up to that point.
To know more about probability visit:
https://brainly.com/question/31828911
#SPJ11
Hannah has liabilities totaling $30,000 (excluding her mortgage of $100,000 ). Her net worth is $45,000. What is her debt-to-equity ratio? 0.75 0.45 0.67 1.30 1.00
Answers
Hannah's debt-to-equity ratio when her liabilities was $30,000 (excluding her mortgage of $100,000 ) and her net worth is $45,000 is 0.75.
Debt-to-equity ratio is a financial ratio that measures the proportion of total liabilities to shareholders' equity. To calculate the debt-to-equity ratio for Hannah, we need to first calculate her total liabilities and shareholders' equity.
We are given that Hannah has liabilities of $30,000 excluding her mortgage of $100,000. Therefore, her total liabilities are $30,000 + $100,000 = $130,000.
We are also given that her net worth is $45,000. The net worth is calculated by subtracting the total liabilities from the total assets. Therefore, the shareholders' equity is $45,000 + $130,000 = $175,000.
Now we can calculate the debt-to-equity ratio by dividing the total liabilities by the shareholders' equity.
Debt-to-equity ratio = Total liabilities / Shareholders' equity = $130,000 / $175,000 = 0.74 (rounded to two decimal places)
Therefore, Hannah's debt-to-equity ratio is 0.74, which is closest to option 0.75.
Learn more about Debt-to-equity ratio here: https://brainly.com/question/27993089
#SPJ11
If f(x) = 3x-6 and g(x) = 1/3x+1, then (g(f))^-1 (x) equals.
1-x
1/3(3x-1)
(x+1)
(x-1)
Answers
We need to find the inverse of the function gof (x). First we need to find the composite function gof (x) which is given by:
\(g(f(x)) = g(3x - 6)\)
= \((1/3)(3x - 6) + 1\)
= x - 1 + 1
= x
Thus,
gof (x) = x.
Now we need to find the inverse of the function gof (x) to obtain
\((gof)^-1 (x).\)
We have gof (x) = x
which implies\((gof)^-1 (x)\)
= gof (x)^-1
= x^-1
= 1/x,
x ≠ 0
Therefore,
\((gof)^-1 (x) = 1/x\)
which is option (3) (x+1) since 1/x can be written as 1/(x+1-1), where (x+1-1) is the denominator of 1/x.
Hence, the correct option is (3).
To know more about two functions visit:
https://brainly.com/question/19517220
#SPJ11
To find (g(f))^-1 (x), substitute the expression for f(x) into g(x) and simplify. The composition of g(f) is x and its inverse is also x. Therefore, (g(f))^-1 (x) equals x.
Explanation:To find (g(f))^-1 (x), we need to first find the composition of g(f) and then find its inverse. Start by substituting the expression for f(x) into g(x): g(f(x)) = g(3x-6) = \frac{1}{3}(3x-6) + 1 = x - 1 + 1 = x. So, g(f(x)) = x. Now, to find the inverse of g(f), we switch the x and y variables and solve for y: y = x. Therefore, (g(f))^-1 (x) = x.
Learn more about Composition of Functions here:https://brainly.com/question/33783470
#SPJ12
Polynomial uing Remainder Theorem and Factor Theorem checking uing ynthetic diviion. X^4 - x^3 - 3x^2 4x 2 ÷ (x 2)
Answers
The remainder of the polynomial using the remainder theorem and factor theorem is 6.
Apply the remainder theorem,
When we divide a polynomial
f(x) by (x − c)
f(x) = (x − c)q(x) + r
f(c) = 0 + r
Here,
f(x)=(x−c)q(x)+rf(c)=0+r
and (x−c) is (x−(−2))
Therefore,
f(−2) = \((-2)^{4} - (-2)^3 - 3(-2)^2 + 4(-2) + 2\)
= 16 + 8 − 12 − 8 + 2
= 6
Hence, the remainder of the polynomial using the remainder theorem is 6.
Whereas using the factor theorem and doing synthetic division, we get,
x = -2 is a zero of f(x), and x+2 is a factor of f(x). To factor f(x), we divide
the coefficients of the polynomial as follows -
-2 | 1 -1 -3 4 2
-2 6 -6 4
-----------------------------------------
1 -3 3 -2 6
Hence, we get that 6 is the remainder when (\(x^4-x^3-3x^2+4x+2\)) ÷ (x+2), using the factor theorem.
Read more about factor theorem:
brainly.com/question/19030198
#SPJ4
The complete question is -
Find the remainder using the Remainder Theorem and Factor Theorem using the synthetic division of the given polynomial, \(x^4-x^3-3x^2+4x+2\) ÷ (x+2)
can someone please answer this for me -11p + 11p
Answers
Answer:
ooouuhhggg
Step-by-step explanation:
iiiiijhhhjjjhhjjjnnnnnnjjj
Answer:
0
Step-by-step explanation:
-11p + 11p
=> 0
ILL GIVE BRAINLIEST TO WHOE ER ANSWERS

Answers
Answer:
I would say the answer would be a
It is the middle of the heatwave, and you AC unit has broken. You have 2 companies that come highly qualified. Company A charges $200 to come out plus $50 per hour to look at your AC and determine what is wrong. Company B charges $125 plus $75 an hour for the same exact service.
After how many hours (x) will both companies charge you the same amount(y)?
Answers
By solving a linear equation, we will see that after 3 hours, both companies will charge the same amount.
After how many hours will both companies charge you the same amount?
We know that company A charges $200 plus $50 per hour. So if they work for x hours, they charge:
A(x) = $200 + $50*x
And company B charges $125 plus $75 per hour, so if they work for x hours, they charge:
B(x) = $125 + $75*x
We want to find the value of x such that A(x) = B(x), then we want to solve the linear equation:
$200 + $50*x = $125 + $75*x
$200 - $125 = $75*x - $50*x
$75 = $25*x
$75/$25 = x = 3
This means that after 3 hours, both companies will charge the same amount.
If you want to learn more about linear equations:
https://brainly.com/question/1884491
#SPJ1
what is the name of the length of the straight line drawn from an object’s initial position to the object’s final position?
Answers
Displacement is the length of the straight line drawn from an object’s initial position to the object’s final position
The term "displacement" refers to a change in an object's position. It is a vector quantity with a magnitude and direction. The symbol for it is an arrow pointing from the initial position to the ending position. For instance, if an object shifts from position A to position B, its position changes.
If an object moves with respect to a reference frame, such as when a passenger moves to the back of an airplane or a professor moves to the right with respect to a whiteboard, the object's position changes. This change in location is described as displacement.
The displacement is the shortest distance between an object's initial and final positions. Displacement is a vector. It is visualized as an arrow that points from the initial position to the final position, indicating that it has both a direction and a magnitude.
Learn more about displacement at:
https://brainly.com/question/14422259
#SPJ4
every bounded infinite closed set contains a rational number
Answers
The statement is incorrect. Not every bounded infinite closed set contains a
rational number.
A bounded infinite closed set may or may not contain a rational number. It depends on the specific set in question.
For example, consider the set of real numbers between 0 and 1, denoted as
[0, 1].
This set is bounded (since it is contained within the interval [0, 1]) and closed (as it includes its boundary points 0 and 1). However, this set contains irrational numbers such as
√2
and π, but it does not contain any rational numbers.
On the other hand, if we consider the set of rational numbers between 0 and 1, denoted as
(0, 1)∩ℚ,
this set is bounded, infinite, and closed. It contains only rational numbers, but no irrational numbers.
Therefore, it is incorrect to claim that every bounded infinite closed set contains a rational number. The presence or absence of rational numbers in a given set depends on the
specific elements
and properties of that set.
To learn more about
Rational Number
brainly.com/question/17450097
#SPJ11
Step 2 - Fill in the missing number: A vertical line and horizontal line combine to make a L shape. There is one row of entries in the shape including 1, negative 3, negative 10, 24. On the outside to the left of the L shape is 2 and to the outside below 1 is a. a =
Answers
The synthetic division's representation of the dividend is 2x3 + 10x2 + x + 5.
Given that
An L shape is created when two lines intersect vertically and horizontally.
The shape has entries in two rows.
Entries in row 1 are 2, 10, 1, and 5.
Blank, -10, and 0 are the entries in row 2.
A simplified method of dividing a polynomial with another polynomial equation of degree one is known as synthetic division.
On the exterior, to the left of the form, is entry number 5.
The entry stands for the divisor's zero.
If the variable is x, then this entry to the variable is;
2x³+10x²+x+5
The dividend is thus represented by synthetic division as
2x³+10x²+x+5
The Question is incomplete And complete question is given below!!
What dividend is represented by the synthetic division below? A vertical line and horizontal line combine to make a L shape. There are two rows of entries within the shape. Row 1 has entries 2, 10, 1, 5. Row 2 has entries blank, negative 10, 0, negative 5. Entry negative 5 is on the outside to the left of the shape, and a third row of entries is outside and below the shape. Row 3 has entries 2, 0, 1, 0. Negative 10 x squared minus 5 2 x cubed 10 x squared x 5 2 x squared 1 2 x cubed x.
Learn more about Synthetic division here
https://brainly.com/question/27979968
#SPJ1
Answer:
The answer on Edge is A= 1
Step-by-step explanation:
#1. The area of a square tile is 53.4cm^2. find the length of one side of the tile, rounded to the nearest 10th.
#2 which RADICAL is not a perfect square
a)5.29
b)13.69
c)1.3
d)0.09
#3 A walkway is been constructed using square cement tiles that each have an area of 15.5ft^2. Six tiles will be lined up end to end to construct a walkway. What is the total length of the walkway? Round your answer to the nearest 10th of a foot.
PLEASE ANSWER ASAP
all of them or even one would help please please
Answers
Problem 1
Answer: 7.3Explanation: Apply the square root to the area to get the side length. This only applies to areas that are squares (hence the name).
==================================================
Problem 2
Answer: C) 1.3Explanation: Use your calculator to find that choices A,B,D plugged into the square root function yield terminating decimal values. "Terminating" means "stop". This implies that they are perfect squares (though not perfect squares in the sense of whole number perfect squares which you may be used to). Choice C is the only value that has a square root that leads to a non-terminating decimal. The digits of this decimal go on forever without any pattern. The value is irrational.
sqrt(5.29) = 2.3 terminating decimalsqrt(13.69) = 3.7 terminating decimalsqrt(1.3) = 1.140175425 keeps going forever without any patternsqrt(0.09) = 0.3 terminating decimal==================================================
Problem 3
Answer: 23.6 feet approximatelyExplanation: Apply the square root to 15.5 to get roughly 3.937; this is the approximate side length of one square. Six of these tiles placed together will lead to a total length of roughly 6*3.937 = 23.622 which rounds to 23.6 feet. Like with problem 1, the square root being used like this only works for square areas.
John's health club has an enrollment fee of $200 and costs $45 a month. The total cost of the membership is a function of the number of months. The function is represented by f(x)=45x+200. If the domain is 12 months, what is the range. Find the range and EXPLAIN how you found it.
Answers
Answer:
f(x)=740
Step-by-step explanation:
f(x)=45x+200
If f(12)
f(x) = 45(12) +200
f(x) = 540 +200
f(x)=740
The range is 740 and we get the range by substituting x = 12 in the given function.
Given,
John's health club has an enrollment fee of $200 and costs $45 a month. The total cost of the membership is a function of the number of months. The function is represented by f(x)=45x+200.
The domain is 12 months.
We need to find the range and explain it.
What is a domain and range of a function?The domain is the input value and the range is the output value of the given function.
We have a function:
f(x) = x + 1
f(1) = 1 + 1 = 2
Domain = 1.
Range = 2.
Find the range of f(x) = 45x + 200.
We have,
Domain = 12 months.
x = 12.
f(12) = 45 x 12 + 200
= 540 + 200
= 740.
Thus the range is 740 and we get the range by substituting x = 12 in the given function.
Learn more about finding the range of a function here:
https://brainly.com/question/27954457
#SPJ2
A highway curve has a backsite with a bearing of N 10°E and deflection angle (intersection angle) of 57°. If the horizontal curve has a degree of curvature (arc definition), D, of 5° what is the stationing of PT if the stationing of PC is 6+88 You must accurately draw and label the horizontal curve to receive full points.
Answers
To determine the stationing of PT on the horizontal curve, we need to consider the given information of the backsite bearing, deflection angle, and degree of curvature. By utilizing the stationing of PC, which is 6+88, we can calculate the stationing of PT.
The backsite bearing of N 10°E indicates that the tangent line extends 10° east of north. The deflection angle of 57° signifies the change in direction from the tangent line to the chord connecting PC and PT. The degree of curvature D, which is 5°, provides the angular change per station.
To calculate the stationing of PT, we need to determine the length of the curve between PC and PT. This can be done by dividing the deflection angle (57°) by the degree of curvature (5°) to obtain the number of stations. In this case, the length of the curve is 57° / 5° = 11.4 stations.
Next, we add the length of the curve (11.4 stations) to the stationing of PC (6+88) to find the stationing of PT. The stationing of PT is 6+88 + 11.4 = 18+28.4.
In summary, the stationing of PT on the horizontal curve, given a backsite bearing of N 10°E, a deflection angle of 57°, and a degree of curvature of 5°, is 18+28.4.
know more about deflection angle :brainly.com/question/22953155
#SPJ11
what shape do i draw?

Answers
Answer:
You draw the exact same shape but at a different scale
Step-by-step explanation:
You just draw it bigger.
Find the equation of the parabola with its focus at (-7,6) and its directrix at y = 4
OA) y-/a(x + 7)2 + 5
O B) y-/Ax+ 7)2 + 5
Ooy-/ax- 72 +5
OD) y- 1/4lx+ 5)2+7
Answers
Answer:
Your choices of answers are confusing , but It looks like A is a good fit
Step-by-step explanation:
\(x^{2}\) + 14x +54 ( from drawing ) [ leave the web address for the graphing webpage so you can use it to check answers]
complete the square on the above expression
\(x^{2}\) +14x + \(7^{2}\) + 54 - 49 ( b/c we added 49 to complete square)
(x+7)^2 + 5
So this looks a bit like answer A

Saul solves the quadratic equation x^2 + 5x - 5=0 using the quadratic formula. In
which step did Saul make an error?

Answers
please convert the following unsigned binary number to base 10. 100101 question 54 options: 101 21 53 37
Answers
The unsigned binary number 100101 is equal to 18 in base 10. The provided options (101, 21, 53, 37) do not match the conversion result.
The provided options (101, 21, 53, 37) do not match the conversion result of unsigned binary number to base.
To convert the unsigned binary number 100101 to base 10, we can use the following steps:
1. Identify the place values for each digit: (2^4) (2^3) (2^2) (2^1) (2^0)
2. Multiply the binary digits with their respective place values: (1×2^4) (0×2^3) (0×2^2) (1×2^1) (0×2^0)
3. Add the results: (16) + (0) + (0) + (2) + (0) = 18
To know more about unsigned binary:
https://brainly.com/question/12966397
#SPJ11
simplify (a+b)/(a^2+b^2)*a/(a-b)*(a^4-b^4)/(a+b)^2
Answers
We can start by simplifying each factor separately and then combine them.
(a + b)/(a^2 + b^2) can be simplified by multiplying both the numerator and denominator by (a - b):
(a + b)/(a^2 + b^2) * (a - b)/(a - b) = (a^2 - b^2)/(a^3 - b^3)
Next, we simplify a/(a - b) by multiplying both the numerator and denominator by (a + b):
a/(a - b) * (a + b)/(a + b) = a(a + b)/(a^2 - b^2)
Lastly, we simplify (a^4 - b^4)/(a + b)^2 by factoring the numerator and expanding the denominator:
(a^4 - b^4)/(a + b)^2 = [(a^2)^2 - (b^2)^2]/(a + b)^2 = [(a^2 + b^2)(a^2 - b^2)]/(a + b)^2
Now we can combine all three simplified factors:
(a + b)/(a^2 + b^2) * a/(a - b) * (a^4 - b^4)/(a + b)^2 = [(a^2 - b^2)/(a^3 - b^3)] * [a(a + b)/(a^2 - b^2)] * [(a^2 + b^2)(a^2 - b^2)]/(a + b)^2
Simplifying further, we can cancel out the (a^2 - b^2) terms and the (a + b) terms:
= [a(a + b)/(a^3 - b^3)] * [(a^2 + b^2)/(a + b)]
= a(a + b)(a^2 + b^2)/(a + b)(a^3 - b^3)
= a(a^2 + b^2)/(a^3 - b^3)
Therefore, the simplified expression is a(a^2 + b^2)/(a^3 - b^3)
How would you find the volume of this figure? Please give an answer and explain...

Answers
Step 2: Find the volumes of all the triangles. Formula: L * H * 1/2 (Hint: 2 triangles in all. Most likely the same size, if so, just do 1 triangle!!!)
Step 3: Once found all the volumes of the figures, add all the values and that will be the volume of the whole figure!
You are basically breaking up the figure into separate shapes!
Hopefully this helped!!! :)
If the pool is to be 24 ft on each side, what is the length of one side of the hot tub? 4 ft 4.8 ft 6 ft 7.2 ft
Answers
Based on the information given the length of one side of the hot tub is 4. 8 ft. So the correct option is B.
The complete question is given as:-
Ricardo has a square hot tub. He wants to build a square pool next to it that is a dilation of the hot tub using a scale factor of 5. Point Q is the centre of dilation. Square A B C D is dilated to create square A prime B prime C prime D prime. The length of B prime C prime is 24 feet. If the pool is to be 24 ft on each side, what is the length of one side of the hot tub? 4 ft 4.8 ft 6 ft 7.2 ft
What is the scale factor?The scale factor is defined as the proportion of the new image's size to that of the previous image. decision-making.
Length: Using this formula
Length=B prime C prime length/Scale factor
Where:
B prime C prime length=24 feet
Scale Factor=5
Let plug in the formula
Length=24ft/5
Length=4.8ft
In conclusion, the length of one side of the hot tub is 4. 8 ft.
To know more about scale factors follow
https://brainly.com/question/25722260
#SPJ1