Answers
Related Questions
4. The dot plots show how much time, in minutes, students in a class took to complete
each of five different tasks. Select all the dot plots of tasks for which the mean time is
approximately equal to the median time.
A
19
A+
05 10 15 20 25 30 35 40 45 50 55 60
*******
++
++
5 10 15 20 25 30 35 40 45 50 55 60
cos
.
*********
"
****
10 15 20 25 30 35 40 45 50 55 60
*******
.
***H
D
0 5 10 15 20 25 30 35 40 45 50 55 60
.
E ++
0 5 10 15 20 25 30 35 40 45 50 55 60
Answers
Main Answer: The dot plots for tasks A+ and D show the mean time is approximately equal to the median time.
Supporting Question and Answer:
How do we determine if the mean time is approximately equal to the median time based on a dot plot?
To determine if the mean time is approximately equal to the median time based on a dot plot, we need to look at the distribution of the data and see if it is symmetric or skewed. If the data is roughly symmetric, with values distributed evenly on both sides of the median, then the mean and median will be close to each other, and the mean time will be approximately equal to the median time. Conversely, if the data is skewed, with more values on one side of the median than the other, then the mean and median will be further apart, and the mean time will not be approximately equal to the median time.
Body of the Solution:The dot plots of tasks for which the mean time is approximately equal to the median time are:
Dot plot A+: The median is around 25 minutes, and the mean is also around 25 minutes.
Dot plot D: The median is around 20 minutes, and the mean is slightly above 20 minutes.
Therefore, dot plots A+ and D have approximately equal mean and median times.
Final Answer:Thus, dot plots A+ and D have approximately equal mean and median times.
To learn more about determine if mean time is approximately equal to the median time based on a dot plot from the given link
https://brainly.com/question/22761225
#SPJ4
The dot plots for tasks A+ and D show the mean time is approximately equal to the median time.
To determine if the mean time is approximately equal to the median time based on a dot plot, we need to look at the distribution of the data and see if it is symmetric or skewed. If the data is roughly symmetric, with values distributed evenly on both sides of the median, then the mean and median will be close to each other, and the mean time will be approximately equal to the median time. Conversely, if the data is skewed, with more values on one side of the median than the other, then the mean and median will be further apart, and the mean time will not be approximately equal to the median time.
Body of the Solution: The dot plots of tasks for which the mean time is approximately equal to the median time are:
Dot plot A+: The median is around 25 minutes, and the mean is also around 25 minutes.
Dot plot D: The median is around 20 minutes, and the mean is slightly above 20 minutes.
Therefore, dot plots A+ and D have approximately equal mean and median times.
Thus, dot plots A+ and D have approximately equal mean and median times.
To learn more about mean and median
https://brainly.com/question/31098693
#SPJ4
I need the answer because i been trying to figure this out for 20 minutes

Answers
Answer:
sqrt (65) = 8.062 units = x
Step-by-step explanation:
use Pythagorean theorem for a right triangle
a ^2 + b^2 = c^2 where a and b are the legs and c is the hypotenuse
4^2 + x^2 = 9^2
x^2 = 9^2 - 4^2
x^2 = 65
x = sqrt 65
Answer:
c
Step-by-step explanation:
using ratio plz help im stuck i need #5 for one side 1-5 for the other




Answers
Science= 3 * 21 = 63
Math= 5 * 21 = 105
English= 7 * 21 = 147
147- 63 = 84
Answer: 84
—
2) A rope is cut in two in the ratio 3.5:1.75. The difference between the length is 94.5 inches. What was the original length of the rope?
3.5+1.75= 5.25
94.5 + 5.25 = 99.75
Answer: 99.75
—
3) A room is 14 feet long. Find the width of the room, if the ratio of the length to the width of the room is 7:5.
Length= 14
7 • 2 = 14
5 • 2 = 10
Answer: 10 feet
—
4) Steve covers a distance of 0.7 miles in 2 minutes. How much time will it take to travel 14 miles?
0.7 miles in 2 minutes
2 • 7 = 14
0.7 • 7 = 4.9
Answer: 4.9 miles
—
5) Lara and Mae are collecting seashells. For every 9 seashells that Lara picked, Mar gathered 7 seashells. If Lara collected 63 seashells, how many fewer seashells did Mae gather?
Let’s get out the key words here.
Lara gathers 9
Mae gathers 7
Lara collects 63
Mae collects ?
**Fewer seashells**
9 • ? = 63
9 • 7 = 63
This means she would need to gather 9 seashells 7 times to get 63 seashells.
This means Mae would need to get 7 shells 7 times to get her fewer amount.
7 • 7 = 49
Mae would gather 49 seashells. But it says fewer seashells.
63- 49 = 14
Final Answer: Mae would gather 14 less seashells then Lara.
—
5) A sum of 2,700 is shared among Eric, Jo, and Richard. Jo’s share is two times that of Richard’s share. Eric’s share is three times that of Jo’s share. Find Eric’s share.
2700/3= 900
900*2= $1,800
Answer: $1,800
—
I’m not sure if all of the answers are right but I hope this still helps you :)
Assume that a sample is used to estimate a population mean μ . Find the 98% confidence interval for a sample of size 73 with a mean of 29.4 and a standard deviation of 21.3. Enter your answer as an open-interval (i.e., parentheses) accurate to 3 decimal places.98% C.I. = The answer should be obtained without any preliminary rounding.
Answers
Given:
sample size = 73
mean = 29.4
standard deviation = 21.3
To find:
98% confidence interval for the sample size and mean
To get the confidence interval, we'll apply the formula:
\(\begin{gathered} \bar{x}\text{ }\pm\text{ Z}\frac{s}{\sqrt{n}} \\ where\text{ s= standard deviation} \\ \bar{x}\text{ = mean} \\ Z\text{ = 98\% z score} \end{gathered}\)\(\begin{gathered} confidence\text{ interval = 29.4 }\pm\text{ Z }\frac{21.3}{\sqrt{73}} \\ Z\text{ = 98\% confidence = 2.326} \\ \\ Confidence\text{ interval = 29.4 }\pm\text{ 2.326 }\times\text{ }\frac{21.3}{\sqrt{73}} \end{gathered}\)\(\begin{gathered} Confidence\text{ interval = 29.4 }\pm\text{ 5.7987} \\ \\ Conf\imaginaryI dence\text{ }\imaginaryI\text{nterval = 29.4 +5.7987 or 29.4 - 5.7987} \\ \\ Confidence\text{ interval = 35.1987 or 23.6013} \\ \\ To\text{ 3 decimal place, upper bound = 35.199 and lower bound = 23.601} \end{gathered}\)\(98\text{ \% C.I. = \lparen23.601, 35.199\rparen}\)Your living room is carpeted but you have allergies, and need to cover the 9 points floor with hardwood panel flooring. The panel flooring at Lowes cost $3.19 per square foot. (scale: 1m = 3.28 ft) Hint: Each unit contains 32.29 square feet. How much will it cost to purchase the flooring panels? (round to the nearest cent)
HELPPPPPPPP
Answers
Answer:
$103
Step-by-step explanation:
Your living room is carpeted but you have allergies, and need to cover the 9 points floor with hardwood panel flooring. The panel flooring at Lowes cost $3.19 per square foot. (scale: 1m = 3.28 ft) Hint: Each unit contains 32.29 square feet. How much will it cost to purchase the flooring panels? (round to the nearest cent)
From the above question:
1 square foot = $3.19
32.29 square feet = x
Cross Mulitiply
x = 32.29 × $3.19
x = $103.0051
Approximately to the nearest cent = $103
Therefore, it will cost $103 to purchase the flooring panels
In a completely randomized experimental design involving five treatments, 13 observations were recorded for each of the five treatments (a total of 65 observations). Also, the design provided the following information.
SSTR = 300 (Sum of Squares Due to Treatments)
SST = 800 (Total Sum of Squares)
The number of degrees of freedom corresponding to within-treatments is
a. 5.
b. 59.
c. 4.
d. 60.
Answers
The number of degrees of freedom corresponding to within-treatments is 60, which is option (d).
In a completely randomized experimental design, the total sum of squares (SST) can be partitioned into two components: the sum of squares due to treatments (SSTR) and the sum of squares within-treatments (SSE). The degrees of freedom associated with each component are used to analyze the variability in the data.
Given that SSTR = 300 and SST = 800, we can calculate the sum of squares within-treatments (SSE) by subtracting SSTR from SST: SSE = SST - SSTR = 800 - 300 = 500.
The degrees of freedom corresponding to within-treatments is equal to the total number of observations minus the number of treatments. In this case, there are 65 observations (13 observations for each of the 5 treatments) and 5 treatments. Therefore, the degrees of freedom for within-treatments is 65 - 5 = 60.
Hence, the correct answer is option (d), which states that the number of degrees of freedom corresponding to within-treatments is 60.
Learn more about degrees of freedom here:
https://brainly.com/question/32093315
#SPJ11
what postúlate proves the triangle congruent
a.ASA
b.HL
c.SAS
d.SSS
e.AAS

Answers
Side one is the same on both, then the angle, then the second side
Look at the histogram below which data set could be represented by the histogram

Answers
Answer:
Option 4 is correct
Step-by-step explanation:
Here, we want to select from the options, the dataset that is represented on the histogram
From what we have in the question, there is a range from 60 to 100
Also, there are no terms between 70 and 80
option 1 is wrong as we can see terms between 70 and 80
option 2 is also wrong for this reason
option 3 is incorrect ; looking at the frequency, the numbers between 60 and 70 should be 5 only and we have 6 in that set
Option 4 is the correct answer
I will give u brainliest

Answers
option 1 is correct , trigonometric ratio to solve for the missing side is sine.
How can we find the trigonometric ratio ?we have an angle of 54 degrees and a hypotenuse of 12 units. We can use trigonometric ratios to solve for the missing side, which is the perpendicular side.
In a right triangle, the three primary trigonometric ratios are:
Sine (sin): the ratio of the length of the side opposite the angle to the hypotenuse.
Cosine (cos): the ratio of the length of the side adjacent to the angle to the hypotenuse.
Tangent (tan): the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
Given that we know the hypotenuse (12 units) and the angle (54 degrees), we can use the sine ratio to solve for the length of the perpendicular side. The sine ratio is defined as:
sin(x) = opposite/hypotenuse
Plugging in the given values:
sin(54 degrees) = opposite/12
To solve for the length of the perpendicular side (opposite), we can rearrange the equation:
opposite = sin(54 degrees) * 12
Using a calculator, we can find the value of sin(54 degrees) and multiply it by 12 to find the length of the perpendicular side.
therefore, option 1 is correct , trigonometric ratio to solve for the missing side is sine.
To learn more about , trigonometric ratio visit:
https://brainly.com/question/25122825
#SPJ1
Which of these expressions are equivalent to 4x+2(2x−5)−(3−5x) ? Choose the TWO correct answers.
a- 3x−13
b- 13x−13
c- 8x−5−3−5x
d- 8x−10−3−5x
e- 8x−10−3+5x
Answers
Answer:
4x+2(2x−5)−(3−5x) = 8x-10-3+5x
Step-by-step explanation:
We need to find the equivalent expression to 4x+2(2x−5)−(3−5x).
Using distributive property as follows :
a(b+c) = ab+ac
4x+2(2x−5)−(3−5x) = 4x+4x-10-3+5x
= 8x-10-3+5x
Option (e)
Hence, the correct option is (e) "8x-10-3+5x"
Solve for x: help me

Answers
Answer:
\(8x - 4 = 60 \\ 8x = 64 \\ x = 8\)
Answer:
8
Step-by-step explanation:
8x-4=60
Describe the general properties of rotations.
Answers
A rotation maps a line to a line, a ray to a ray, a segment to a segment, and an angle to an angle.
A rotation preserves lengths of segments.
A rotation preserves measures of angles. Step-by-step explanation:
You Welcome :)!
Pr. #1)∫▒〖c √(y+2z-x^2 ds)〗, C is the line segment from (3, 2, 4) to (4,4,7)
Answers
The integral ∫(c √(y+2z-x^2) ds) along the line segment C from (3, 2, 4) to (4, 4, 7) involves integrating the square root of a function of the variables y, z, and x along the line segment C.
To evaluate the integral, we first need to parameterize the line segment C. Let's denote the parameter as t, which varies from 0 to 1. The parameterization of C is given by r(t) = (3 + t, 2 + 2t, 4 + 3t).
Next, we need to compute the differential element ds. The differential element ds represents an infinitesimally small length along the line segment C and is given by ds = |r'(t)| dt, where r'(t) is the derivative of r(t) with respect to t.
Taking the derivative of r(t), we have r'(t) = (1, 2, 3), which has a constant magnitude of √14.
Substituting the parameterization and the differential element into the integral, we have ∫(c √(y+2z-x^2) ds) = ∫(c √(2 + 6t - (3 + t)^2) √14 dt) from 0 to 1.
To evaluate this integral, we substitute the limits of integration and integrate the function with respect to t, taking into account the constant c and the constant factor √14. The detailed calculation will provide the final numerical value of the integral.
To learn more about differential click here:
brainly.com/question/31383100
#SPJ11
When an uncertain event is expressed as a set of possible values, these values are often combined with their respective probabilities into a single mean value called what
Answers
When an uncertain event is expressed as a set of possible values, these values are often combined with their respective probabilities into a single mean value called the expected value or the mathematical expectation.
The expected value is a concept used in probability theory and statistics to represent the long-term average outcome of a random variable or uncertain event. It is calculated by multiplying each possible value of the event by its corresponding probability and summing up these products. The result is a single value that represents the average or mean outcome of the event.
The expected value provides a way to summarize the overall outcome of an uncertain event in a single numerical value. It serves as a useful tool in decision-making and risk analysis, as it helps to assess the potential outcomes and evaluate the potential gains or losses associated with different probabilities. By considering the expected value, individuals or organizations can make informed decisions based on the average outcome of the event and weigh the potential risks and rewards.
Learn more about probability here:
https://brainly.com/question/30034780
#SPJ11
PLEASE HELP FAST!
A cylinder and a cone have the same volume. The cylinder has radius x
and height y. The cone has radius 1/2x. Find the height of the cone in terms of y.
Answers
The height of the cone in terms of y is h = 12x⁴y
How to find the volume of a cone and cylinder?The cylinder and the cone have the same volume.
Volume of a cylinder = πr²h
where
r = radiush = heightTherefore,
Volume of a cylinder = πx²y
volume of a cone = 1 / 3 πr²h
where
r = radius of the coneh = height of the coneTherefore,
πx²y = 1 / 3 × π × (1 / 2x)² × h
πx²y = πh / 12x²
πx²y × 12x² / π = h
h = 12x⁴y
Therefore, the height of the cone in terms of y is h = 12x⁴y
learn more on volume here: https://brainly.com/question/1984638
#SPJ1
What quadrant is point C located in?
A. quadrant I
B. quadrant II
C. quadrant III
D. quadrant IV

Answers
Answer:
it’s in the first one
Step-by-step explanation:
so it’s quadrant I.
Answer:
its A. Quadrant 1
Step-by-step explanation:
I had a test on it :)
Write the fraction decimal and percent for the model below be sure to simplify your fraction

Answers
Answer:
\(\frac{3}{5}\)
0.6
60%
Step-by-step explanation:
Which statements are true about the lines of symmetry of a regular pentagon? Select three options. Every line connects two vertices. Every line connects the midpoints of 2 sides. Every line bisects a vertex angle. Every line bisects a side. Every line is perpendicular to a side.
Answers
Answer:
3,4,5. or C,D,E.
Step-by-step explanation:
Every line bisects a vertex angle.
Every line bisects a side.
Every line is perpendicular to a side.
I took it on Edg and got 100%
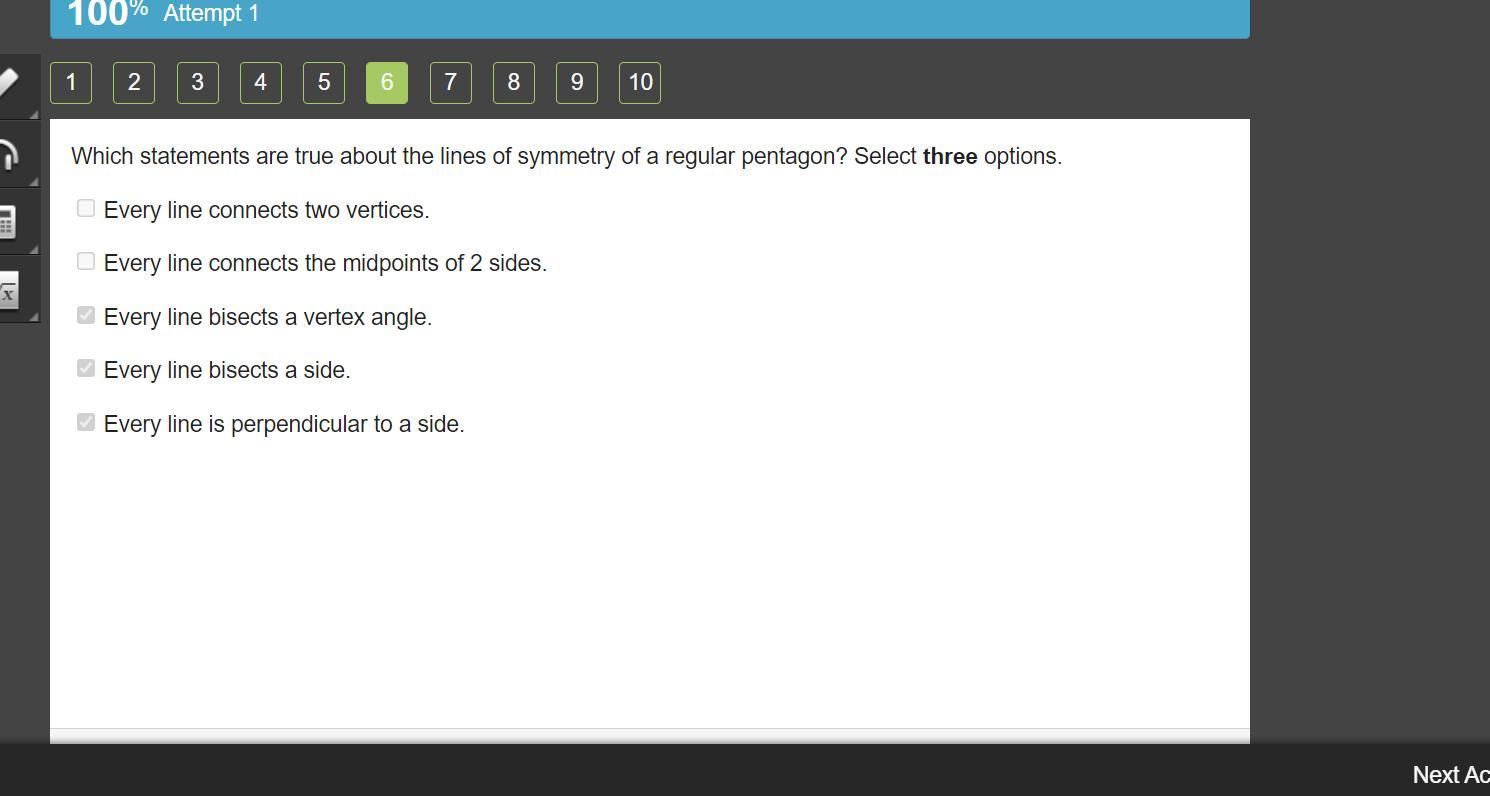
The true statements about the line of symmetry for a regular Pentagon are statements 3, 4, and 5.
What is a regular pentagon?A regular Pentagon is a five-sided polygon whose interior angles are all equals.
We have to given that;
To find statements are true about the lines of symmetry of a regular pentagon.
Hence, The true statements about the line of symmetry for a regular Pentagon are:
Every line bisects a vertex angle.
Every line bisects a side.
Every line is perpendicular to a side.
In conclusion, a regular Pentagon has five equal angles.
Learn more about regular Pentagon at:
brainly.com/question/11759904
#SPJ7
a shopkeeper purchased 1000 electric bulb at rs 16 each. 100 bulbs were damaged and he sold the remaining bulbs at 12.5% profit. find the selling price of each bulb.
Answers
Answer:
The selling price of each bulb is rs 20.
Step-by-step explanation:
Cost price of 1 bulb = rs 16
Cost price of 1000 bulbs = rs 16 × 1000 = rs 16000
Number of bulbs damaged = 100
Number of bulbs sold = 1000 - 100 = 900
Let the selling price of 1 bulb be represented by b
Selling price of 900 bulbs = 900 × b = 900b
Percentage profit = (selling price - cost price) ÷ cost price
12.5% = (900b - 16000) ÷ 16000
900b - 16000 = 0.125 × 16000
900b - 16000 = 2000
900b = 2000 + 16000
900b = 18000
b = 18000/900 = rs 20
Let G be a connected graph with at least one cycle. Prove the following statement: We can remove some edges from G such that the resulting subgraph is bipartite and connected.
Answers
We have shown that for any connected graph G with at least one cycle, we can remove some edges such that the resulting subgraph is bipartite and connected.
What is graph?A graph is a graphic or visual representation of facts or values. The points on a graph are frequently used to depict the relationships between two or more objects.
To prove the statement, let's consider a connected graph G with at least one cycle.
Case 1: G is already bipartite.
If G is already bipartite, then the statement is trivially true. We don't need to remove any edges because G is already bipartite and connected.
Case 2: G is not bipartite.
If G is not bipartite, it means that there exists at least one odd cycle in G. In order to make G bipartite, we can remove any one of the edges from the odd cycle. Removing a single edge will break the cycle and create two separate connected components.
Let's denote the original graph with the odd cycle as G', and the resulting subgraph after removing one edge as G''. By removing a single edge, G'' will consist of two connected components, each of which is bipartite. This is because removing one edge from the odd cycle creates two separate paths, and each path can be assigned a different color to form a bipartite graph.
Since G'' is the result of removing one edge from G', it is still connected because all the vertices in G' are still connected through the remaining edges. Thus, G'' is a connected subgraph of G and is also bipartite.
Therefore, we have shown that for any connected graph G with at least one cycle, we can remove some edges such that the resulting subgraph is bipartite and connected.
Learn more about graph on:
https://brainly.com/question/27877215
#SPJ4
Using the graph
Order the lines from the steepest slope to the least steel slope
Answers
Answer:
The steepest slope is that of the line that is closest to being vertical.Step-by-step explanation:
Hope this helps!!!!Answer:
B, A, C, D
Step-by-step explanation:
rise over run
slope: the ratio of the change in the dependent values (outputs) to the change in the independent values (inputs) between two points on a line
What is 16% of GHc5000.00
Answers
\(\begin{array}{|c|ll} \cline{1-1} \textit{\textit{\LARGE a}\% of \textit{\LARGE b}}\\ \cline{1-1} \\ \left( \cfrac{\textit{\LARGE a}}{100} \right)\cdot \textit{\LARGE b} \\\\ \cline{1-1} \end{array}~\hspace{5em}\stackrel{\textit{16\% of 5000}}{\left( \cfrac{16}{100} \right)5000}\implies 800\)
Which if the following graphs represents all values of x such that x > -3 and x < 2?
Answers
Step-by-step explanation:
The graph that represents all values of x such that x > -3 and x < 2 is the graph of a vertical line segment located between -3 and 2 on the x-axis, but excluding these two points. This can be represented graphically as:
|
|
|
---------x---------
|
|
|
-3 2
Here, the open circles indicate that the points -3 and 2 are not included in the range of values for x.
i need help with this. im confused.

Answers
the national average.
If the national average for a gallon of gas is $2.59, how much
should you expect to pay for gas in Philadelphia versus
Cleveland?
A. $3.03 / $2.75
B. $1.95 / $2.59
C. $2.34 / $2.75
D. $2.75 / $3.24
Philadelphia Clevland
Overall 92 78
Food 106 106
Housing 56 27
Utilities 130 126
Transportation 117 106
Health 102 113
Answers
The correct answer is D. $2.75 / $3.24
To determine how much you should expect to pay for gas in Philadelphia versus Cleveland, we need to compare the transportation expenses in both cities. Based on the given data, the transportation expenses are as follows:
Philadelphia: $117
Cleveland: $106
To calculate the expected gas prices, we need to consider the transportation expenses relative to the national average. The formula to find the expected gas price is:
Expected Gas Price = National Average * (Transportation Expense / National Average)
National Average for gas = $2.59
For Philadelphia:
Expected Gas Price in Philadelphia = $2.59 * ($117 / 92) ≈ $3.30
For Cleveland:
Expected Gas Price in Cleveland = $2.59 * ($106 / 78) ≈ $3.51
Comparing the expected gas prices, we find that:
A. $3.03 / $2.75: This option does not match the expected gas prices in Philadelphia and Cleveland.
B. $1.95 / $2.59: This option does not match the expected gas prices in Philadelphia and Cleveland.
C. $2.34 / $2.75: This option does not match the expected gas prices in Philadelphia and Cleveland.
D. $2.75 / $3.24: This option matches the expected gas prices in Philadelphia and Cleveland.
Therefore, the correct answer is:
D. $2.75 / $3.24
for such more question on transportation expenses
https://brainly.com/question/11734493
#SPJ8
is the angle corresponding, alternate interior, alternate exterior or consecutive interior
Answers
Find the area of the figure.

Answers
132 cm² is the area of the given figure.
To find the area of the figure we need to divide it into two parts such as a rectangle with the dimension of 20 * 6 and a triangle with the dimension of (10 - 6) * (20 - (8 + 6)).
So,
the height of the triangle = 10 - 6 = 4 cm
the base of the triangle = 20 - (8 + 6) = 20 - 14 = 6 cm
Thus,
the area of the triangle = 1/2 * base * height
= 1/2 * 6 * 4
= 12 square cm
Area of the rectangle = length * width
= 20 * 6
= 120 square cm
Thus, the area of the figure will be = 120 + 12 = 132 square cm.
Learn more about Area here:
https://brainly.com/question/27683633
#SPJ1
Simplify (-8a¹b) (3a³b).
a) -24a7b²
b) -5a7b²
c) -5a¹26
d) -24a¹26²
Answers
A function is a mathematical rule that.....
A. Has one or more exponential expressions
B. Can be graphed as a straight line
C. Sends every input to only one output
D. Sends every output to only one input
Answers
Answer:
B
Step-by-step explanation:
A function can be graphed as a straight line, as long as it isn't vertical.
Statement 1: a figure is a polygon offend, only if all of its sides are in a line segments
Statement 2: I figure is not a polygon, if, and only, if not all of it sides are line segments.

Answers
The inverse of a biconditional statement is not equivalent to the original statement. The inverse statement may have a different meaning or convey a different condition.
The inverse of a biconditional statement involves negating both the "if" and the "only if" parts of the statement. In this case, the inverse of the biconditional statement would be:Inverse of Statement 1: A figure is not a polygon if and only if not all of its sides are line segments.
Now, let's analyze the relationship between Statement 2 and its inverse.
Statement 2: A figure is not a polygon if and only if not all of its sides are line segments.
Inverse of Statement 2: A figure is not a polygon if and only if all of its sides are line segments.
The inverse of Statement 2 is not equivalent to Statement 1. In fact, the inverse of Statement 2 is a different statement altogether. It states that a figure is not a polygon if and only if all of its sides are line segments. This means that if all of the sides of a figure are line segments, then it is not considered a polygon.
In contrast, Statement 1 states that a figure is a polygon if and only if all of its sides are line segments. It affirms the condition for a figure to be considered a polygon, stating that if all of its sides are line segments, then it is indeed a polygon.
For more such question son inverse visit:
https://brainly.com/question/3831584
#SPJ8
