i need help with these asap i will award brainleast for whoever gets it right *ONLY ANSWER IF U KNOW PLEASE*

Answers
Answer:
Q1) a = 60
Q2) A = 64
Q3 = A =
Related Questions
what is the solution to the inequality -x/10>-11
Answers
Answer:
x<110
Step-by-step explanation:
-x/10>-11
-x>-11*10
-x>-110
x>110
x<110
Answer:
x > - 110
Step-by-step explanation:
Rearrange the equation by subtracting what is to the right of the greater than a sign from both sides of the inequality :
x / 10 - ( -11 ) > 0
x
Simplify ——
10
x
—— - -11 > 0
10
Subtracting a whole from a fraction
Rewrite the whole as a fraction using 10 as the denominator :
-11 -11 • 10
-11 = ——— = ————————
1 10
Equivalent fraction: The fraction thus generated looks different but has the same value as the whole
Common denominator: The equivalent fraction and the other fraction involved in the calculation share the same denominator
Adding up the two equivalent fractions
Add the two equivalent fractions which now have a common denominator
Combine the numerators together, put the sum or difference over the common denominator then reduce to lowest terms if possible:
x - (-11 • 10) x + 110
——————— = ———————
10 10
x + 110
——————— > 0
10
Multiply both sides by 10
Subtract 110 from both sides
x > -110
Inequality plot for
0.100 x + 11.000 > 0
x > -110
the soccer field at bianca’s school has a length of 120 yards and a width of 85 yards. if she runs across the diagonal from one corner to another, how far does she run, in yards? round your answer to the nearest tenth.
Answers
The distance that she runs from one corner of the field to another is given as follows:
147.1 yards.
What is the Pythagorean Theorem?The Pythagorean Theorem states that for a right triangle, the length of the hypotenuse squared is equals to the sum of the squared lengths of the sides of the triangle.
The distance in this problem is the diagonal of a rectangle, which is the hypotenuse of a right triangle in which the length and the width are the sides, hence:
d² = 85² + 120²
d = sqrt(85² + 120²)
d = 147.1 yards.
More can be learned about the Pythagorean Theorem at brainly.com/question/30203256
#SPJ1
Which of the following points would be a solution to this system of linear inequalities?

Answers
Let's plug in both x and y values in the equation and check if the inequality is true...
\(\red{ \rule{35pt}{2pt}} \orange{ \rule{35pt}{2pt}} \color{yellow}{ \rule{35pt} {2pt}} \green{ \rule{35pt} {2pt}} \blue{ \rule{35pt} {2pt}} \purple{ \rule{35pt} {2pt}}\)
\((4,1) \\ y \leqslant x + 1 \\ y < - \frac{x}{2} - 1\)
Substitute x as 4 and y as 1
\(1 \leqslant 4 + 1 \\ 1 < - \frac{4}{2} - 1\)
\(0 \leqslant 4 + 1 \\ 1 < - 2 - 1\)
\(0 \leqslant 5 \\ 1 < - 3\)
This is not a solution because both are not true, Only one equation is giving true as answer which is not correct!~\(\purple{ \rule{300pt}{3pt}}\)
\((0, - 3) \\ y \leqslant x + 1 \\ y < - \frac{x}{2} - 1\)
Substitute x as 0 and y as -3
\( - 3 \leqslant 0 + 1 \\ - 3 < - \frac{0}{2} - 1\)
\( - 3 \leqslant 1 \\ - 3 < - 0 - 1\)
\( - 3 \leqslant 1 \\ - 3 < - 1\)
This is a solution because both are true, Both the equations are true which means the ordered pair is a solution!~Thus, Option B (0,-3) is the correct choice....
Tyson brought a bag of coins into the bank to be counted. The bag contained only nickels and
dimes. There were a total of 220 coins and the total value of those coins was $15.50.
Use what you have learned about systems of linear equations to determine how many of the coin
were nickels and how many were dimes. Then, fill in the blanks below with your answer.
number of nickels is
number of dimes is
Answers
There will be 130 nickels and 90 dimes. 100 nickels is 5 dollars. 90 dimes are 9 dollars. And then there will be 30 left. 30 dimes isn’t 1.50$ bur 30 nickels is 1.50$ so you add the 30 to the nickels and it’ll be exactly 15.50$.
Answer:
15 50..…......................
Convert 0.54. to a decimal In base 3
Answers
Answer:
what does a this mean? .54 is a decimal
[PLS HELP WILL GIVE BRAINLIEST!!]
Determine the value of x.
![[PLS HELP WILL GIVE BRAINLIEST!!] Determine the value of x.](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/78ffCfgc6bRbu4wLj1ssDiteA0wkC1rr.png)
Answers
Answer:
The value of x is 8.1
Step-by-step explanation:
We can use SOH CAH TOA to find our answer.
In this acronym, O is the opposite side, A is the adjacent side, and H is the hypotenuse. S is for the SIN function. C is for the COS function. T is for the TAN function.
We can calculate the length of the string by using the COS function.
So we can say the tangent of angle \(\beta\) is the opposite side divided by the adjacent side.
\(tan( \beta)=\frac{O}{A}\)
We are given the angle and the opposite side. We are looking for the adjacent side.
Lets solve for \(A\).
Take the reciprocal of both sides.
\(\frac{1}{tan(\beta)} =\frac{A}{O}\)
Multiply both sides by \(O\).
\(\frac{1}{tan(\beta)} *O=A\)
We are given
\(\beta=56\textdegree \\O=12\)
\(\frac{1}{tan(56)} *12=A\)
\(A=8.0941022\)
PLEASE HELP!! ASAP !!! WILL MARK BRAINLEST!
Answer choices
○ 0°
○180°
○270°

Answers
Answer:
270° counterclockwise
Step-by-step explanation:
mrs lopez types at a constant rate the constant of proportionality for the relationship between the number of words she types w, and the number of minutes she types m,is 38 write an equation to show this relationship
Answers
The equation that shows the relationship is w = 38m.
Writing an equation to show this relationshipIf Mrs. Lopez types at a constant rate, then the number of words she types is directly proportional to the amount of time she types. We can express this relationship using the formula:
w = km
where w is the number of words typed, m is the number of minutes spent typing, and k is the constant of proportionality.
We are given that k = 38, so we can substitute this value into the formula to get:
w = 38m
Therefore, the equation that shows the relationship between the number of words Mrs. Lopez types and the number of minutes she types is w = 38m.
Read more about proportional relationship at
https://brainly.com/question/28651666
#SPJ1
Write the mathematical model and use Solver to answer the following question:
A farm co-op has 6,000 acres available to plant with corn and soybeans. Each acre of corn requires 9 gallons of fertilizer/herbicide and 0.75 hour of labor to harvest. Each acre of soybeans requires 3 gallons of fertilizer/herbicide and 1hour of labor to harvest. The co-op has available at most 40,501 gallons of fertilizer/herbicide and at most 5,250 hours of labor for harvesting. Find the maximum profit if the profits per acre are $75 for corn and $40 for soybeans. Round your answer to the nearest cent if necessary.
a. $210,000.00
b. $393,750.00
c. $371,255.83
d. $180,004.44
e. $318,744.17
Answers
The maximum profit if the profits per acre are $75 for corn and $40 for soybeans is $371,255.83. Therefore, the correct option is c.
To find the maximum profit from planting corn and soybeans, we can use linear programming. Let's first define the variables and write the constraints.
Let x be the number of acres of corn and y be the number of acres of soybeans.
1. Total acre constraint: x + y ≤ 6,000
2. Fertilizer/herbicide constraint: 9x + 3y ≤ 40,501
3. Labor constraint: 0.75x + y ≤ 5,250
The objective function to maximize is the profit function: P(x,y) = 75x + 40y
Now, we will use the Solver to find the maximum profit:
Step 1: Set up a spreadsheet with the constraints and the objective function.
Step 2: Go to the Data tab and click on Solver. If Solver is not available, you may need to add it in Excel Options.
Step 3: Set the objective function by selecting the cell with the profit function.
Step 4: Choose "Max" for the objective.
Step 5: Add the constraints by selecting the corresponding cells.
Step 6: Click on "Solve" and the Solver will find the optimal values for x and y.
After using Solver, we find that the optimal values are x = 4,363.89 (corn) and y = 1,636.11 (soybeans), which yields a maximum profit of $371,255.83. Therefore, the correct answer is c: $371,255.83
Learn more about Linear programming:
https://brainly.com/question/14309521
#SPJ11
$9000.00 decreased by 0.5% is what?
Answers
Answer:
8955$
It got deleted because an idiot reported me.
how many different license plates consist of five symbols either digits or letters
Answers
There are 60,466,176 different license plates that consist of five symbols, either digits or letters.
To calculate the number of different license plates consisting of five symbols, we need to consider the number of choices for each symbol, which can be either digits (0-9) or letters (A-Z).
Determine the number of choices for each symbol.
There are 10 digits (0-9) and 26 letters (A-Z), so there are a total of 10 + 26 = 36 possible choices for each symbol.
Use the counting principle.
Since there are 5 symbols on the license plate and 36 choices for each symbol, we can use the counting principle to determine the number of different license plates.
The counting principle states that if there are n ways to do one thing and m ways to do another, then there are n x m ways to do both.
Calculate the number of different license plates.
The number of different license plates can be calculated as 36 × 36 × 36 × 36 × 36 = \(36^5\) = 60,466,176.
For similar question on license.
https://brainly.com/question/30490455
#SPJ11
There are a total of 60,466,176 different license plates consisting of five symbols, either digits or letters. This is because there are 26 letters in the English alphabet and 10 digits, so the total number of symbols is 36.
To calculate the number of different license plates consisting of five symbols, we need to consider that each symbol can be either a digit (0-9) or a letter (A-Z). There are 10 digits and 26 letters, so there are 36 possible choices for each symbol.
To find the total number of different license plates, we use the following steps:
1. Determine the number of possible choices for each symbol (36, as explained above).
2. Since there are five symbols in the license plate, raise the number of choices (36) to the power of 5.
3. Calculate the result.
So, the calculation would be:
36^5 = 60,466,176
There are 60,466,176 different license plates that can be created using five symbols with either digits or letters.
to learn more about digits click here:
https://brainly.com/question/14961670
#SPJ11
Which expression is the same as (2a + b)3?

Answers
Answer:
I guess it's A
Step-by-step explanation:
2*2*2+b*b*b
that's 8a³+b³
It's vacation time. You drive 90 miles along a scenic highway and then take a 5-mile run along a hiking trail. Your driving rate is nine times that of your running rate. The graph shows the total time you spend driving and running, f(x), as a function of your running rate, x.
If the total time for driving and running is 3 hours, what is your running rate?
Answers
The running rate is 5 miles per hour.Let's denote the running rate as "r" and the driving rate as "9r" (since the driving rate is nine times the running rate).
To find the running rate, we need to determine the time spent driving and running separately and then add them together to equal 3 hours.
The time spent running can be calculated as the distance divided by the running rate:
Time running = Distance / Running rate = 5 / r
The time spent driving can be calculated similarly:
Time driving = Distance / Driving rate = 90 / (9r) = 10 / r
The total time spent driving and running is given as 3 hours:
Time running + Time driving = 3
5 / r + 10 / r = 3
To solve this equation, we can combine the fractions on the left side:
(5 + 10) / r = 3
15 / r = 3
Next, we can cross-multiply to isolate the variable:
15 = 3r
Dividing both sides by 3, we find:
r = 5
Therefore, the running rate is 5 miles per hour.
learn more about fractions here: brainly.com/question/10354322
#SPJ11
you can run at a speed of 8 mph and swim at a speed of 4 mph and are located on the shore, 6 miles east of an island that is 1 mile north of the shoreline. how far (in mi) should you run west to minimize the time needed to reach the island?
Answers
The minimize the time needed to reach the island is \(\frac{18-\sqrt{3} }{3}\) mi.
Let "x" the distance traveled by land and "y" be distance traveled in the water.
\($t=\frac{x}{8}+\frac{y}{4}$$\)
From triangle,
\($y^2=(6-x)^2+1^2$$$\begin{aligned}y & =\sqrt{36+x^2-12 x+1}=\sqrt{x^2-12 x+37} \\t & =\frac{x}{8}+\frac{\sqrt{x^2-12 x+37}}{4}\end{aligned}$$\)
Now take derivative
A derivative of a function is the rate of change of one quantity over the other. Derivative of any continuous function that is differentiable on an interval [a, b] is derived using the first principle of differentiation using the limits.
\($$\begin{aligned}& t^{\prime}=\frac{1}{8}+\frac{1 \times(2 x-12)}{4 \times 2 \sqrt{x^2-12 x+37}} \\& t^{\prime}=\frac{1}{8}+\frac{2(x-6)}{8 \sqrt{x^2-12 x+37}} \\& \text { Now } t^{\prime}=0 \quad \frac{1}{8}+\frac{2 x-12}{8 \sqrt{x^2-12 x+37}}\end{aligned}$$\)
\(& \frac{1}{8}+\frac{2 x-12}{8 \sqrt{x^2-12 x+37}}=0 \\& -12+2 x+\sqrt{x^2-12 x+37}=0 \\\)
\(& \text { Now } t^{\prime \prime}=\frac{d}{d x}\left(\frac{1}{8}+\frac{2 x-12}{8 \sqrt{x^2-12 x+37}}\right)=0+\frac{1}{4\left(x^2-12 x+37\right)^{3 / 2}} \\\\& \text { At } t=\frac{18-\sqrt{3}}{3} \text {; } t^{\prime \prime}=\frac{1}{4\left(\left(\frac{18-\sqrt{3}}{3}\right)^2-12\left(\frac{18-\sqrt{3}}{3}\right)+37\right)^{3 / 2}}=0.16 > 0 \\\)
\(x=\frac{18-\sqrt{3}}{3}\)
Therefore, the time needed to reach the island is \(\frac{18-\sqrt{3} }{3}\) mi.
For such more questions about time
https://brainly.com/question/18798899
#SPJ4

Can y’all help me with this it’s my last question?
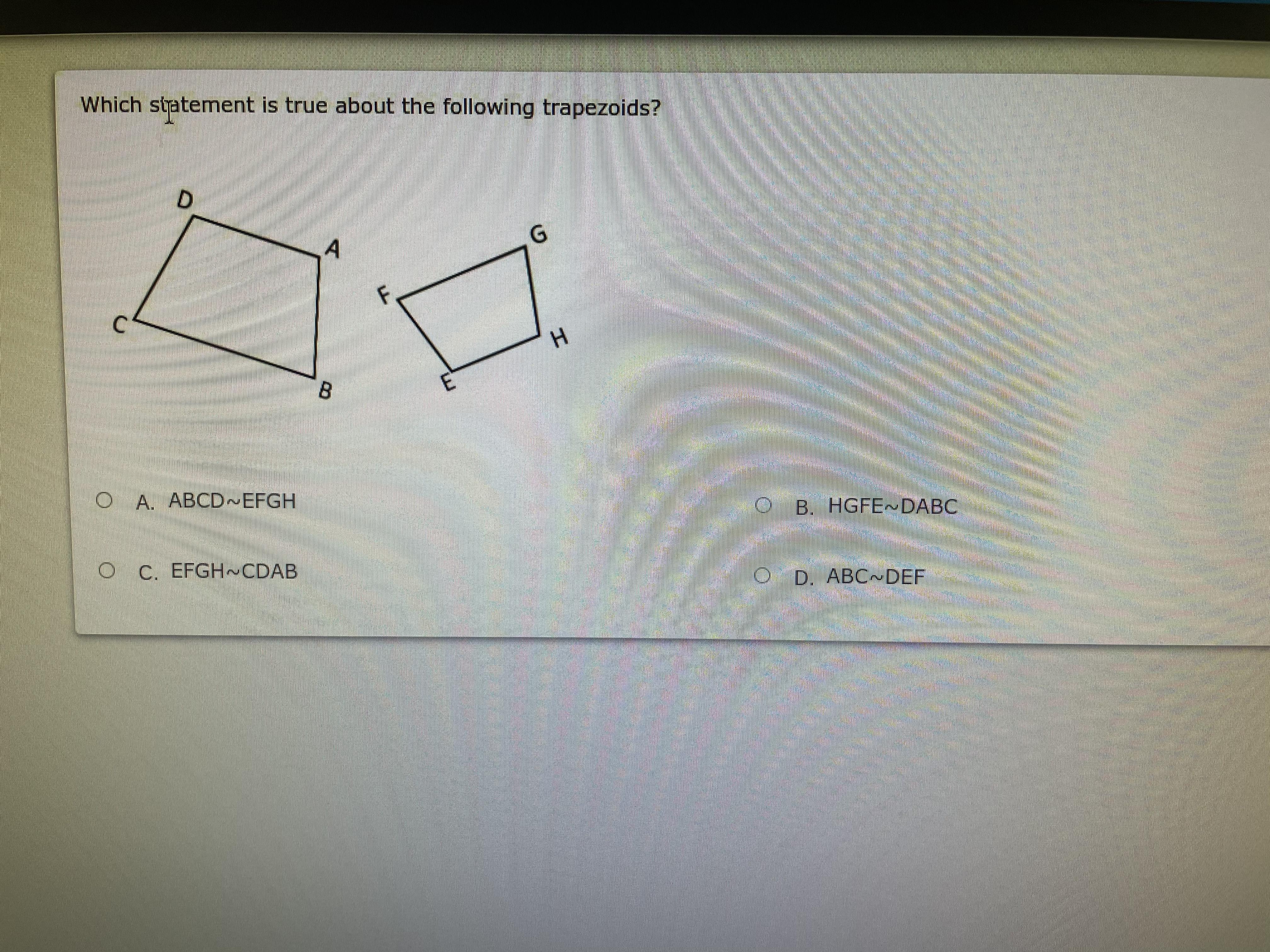
Answers
Answer:
B
Step-by-step explanation:
Answer:
A
Step-by-step explanation:
When doing those statements, the shapes are labelled as a combination of the labels of their angles. The larger trapezoid has angles A, B, C, and D. The smaller one has E, F, G, and H.
When you write statements about multiple shapes, especially when comparing them to one another, you want to make sure those angle labels stay in the SAME ORDER.
Let's say we flipped the little trapezoid upside down. Now it's in the same position as the big one. Then, you'd label them in the order of their congruent angles. A is congruent to E, B is congruent to F, and so on and so forth.
Luckily for us, this stays in alphabetical order. So, ABCD ≅ EFGH.
Consider the following simplified algebraic expression.
10 x squared y + 6 x squared minus 7 y squared minus 6
Which could be the original expression?
Answers
Answer:
*dies of boredom*
Step-by-step explanation:
EH, MWAH
Whats is the value of this expression 1/12 ÷ 36
Answers
Answer:
.00231481
Step-by-step explanation:
\(\frac{1}{12}\) * \(\frac{1}{36}\) = \(\frac{1}{432}\) = .00231481
In 3 hours, 5 people can paint a hall with the area of 750 ft 2. How long would it take for 2 people to paint the hall with the same rate of speed?
Answers
ANSWER:
STEP-BY-STEP EXPLANATION:
In this case, we can make a proportion, since we know the time when there are 5 people, we need to know the time when there are two people
\(\frac{5}{3}=\frac{2}{x}\)solving for x:
\(undefined\)Paul gross weekly salary is $456 what is the maximum monthly rent he can afford?
Answers
Answer:
A metal disk 12cm in diameter and 5cm thick is melted down and cast into a cylindrical bar of diameter 5cm . How long is the bar
4x + 9y = 24
X + y = 10
Help ASAP
Answers
Answer:
14
Step-by-step explanation:
Answer:
(x, y) = (-16/5, 13\(\frac{1}{5}\))
Step-by-step explanation:
4x + 9y = 24
x + y = 10 $\Rightarrow$ x = 10 - y
Substituting the value of x (second equation) into the first equation, we get:
4 * (10 - y) + 9y = 24
40 - 4y + 9y = 24
5y = -16
y = -16/5.
So, x = 10 - (-16/5) = 10 + 3\(\frac{1}{5}\) = 13\(\frac{1}{5}\)
What is this help please

Answers
Explanation:
So the question is asking you to multiply two prime numbers in order to get 21.
Since 3 and 7 are both prime numbers, you can express 21 as 3 x 7
Hope this helps! :)
Here is a list of prime numbers if it helps you. (prime numbers are in blue):

Mr. Mole and Bugs Bunny started digging their way into the ground from different locations at the same time. They each dug at a constant rate. The following equation gives Mr. Mole's altitude (in meters relative to the ground) as a function of time (in minutes). A =-4-0. 6tA=−4−0. 6t Bugs Bunny's altitude (in meters relative to the ground) as a function of time (in minutes) is given by the following table of values: \text{Time}Time (minutes) \text{Altitude}Altitude (meters) 22 -1. 6−1. 6 99 -7. 2−7. 2 1616 -12. 8−12. 8 Who dug faster?
Answers
Comparing the rates of change, we see that Mr. Mole's altitude decreases by 0.6 meters per minute, while Bugs Bunny's altitude decreases by larger amounts per minute (-1.6 meters and -5.6 meters). Therefore, Bugs Bunny dug faster than Mr. Mole.
To determine who dug faster, we need to compare the rates of change of their altitudes over time.
For Mr. Mole, the equation for his altitude (A) as a function of time (t) is given as A = -4 - 0.6t. This means that his altitude decreases by 0.6 meters per minute.
For Bugs Bunny, we can observe the change in altitude from the table of values. The change in altitude between 2 minutes and 9 minutes is -1.6 meters, and the change in altitude between 9 minutes and 16 minutes is -5.6 meters.
know more about rates of change here:
https://brainly.com/question/29181688
#SPJ11
eliminate the parameter in the equations x=5cos(t) -7 and y=5sin(t)+9. how can the rectangular equation be described?
circle
ellipse
parabola
hyperbola
Answers
Answer:
the answer is A
Step-by-step explanation:
The parameters represent a circle with a radius of 5 units, centered at (-7,9) and the equation of the circle is (x + 7)² + (y - 9)² = 5².
Deducing the figure from the parameters:The given equations are:
x = 5cos(t) - 7, and
y = 5sin(t) + 9
if we rearrange the above equations we get:
(x + 7) = 5cos(t), and
(y - 9) = 5sin(t)
Taking square of both equation we get:
(x + 7)² = 25cos²(t), and
(y - 9)² = 25sin²(t)
Now, adding the equations we get:
(x + 7)² + (y - 9)² = 25cos²(t) + 25sin²(t)
(x + 7)² + (y - 9)² = 25
(x + 7)² + (y - 9)² = 5²
This is an equation of a circle with a radius of 5 units and the center at (-7,9)
since, the equation of a circle with radius R units and centered at (a,b) is given by:
(x -a)² + (y - b)² = R²
Learn more about equation of a circle:
https://brainly.com/question/10618691?referrer=searchResults
PLEASE HELP ASAP!!!!!! i’ll mark brainlest

Answers
Answer: A) 5 x 1/2
Step-by-step explanation: 5 x 1/2 yields 2.5, which is also the answer to 5 / 2.
Answer: A. 5 x 1/2
5 divided by 2 is 2.5, and 5 x 1/2 is also 2.5
jamie, a bowler, claims that her bowling score is less than 168 points, on average. several of her teammates do not believe her, so she decides to do a hypothesis test, at a 1% significance level, to persuade them. she bowls 17 games. the mean score of the sample games is 155 points. jamie knows from experience that the standard deviation for her bowling score is 19 points and has reason to assume her scores are normally distributed. h0: μ≥168; ha: μ<168 α
Answers
The null hypothesis (H0) states that the average bowling score (μ) is greater than or equal to 168 points, while the alternative hypothesis (Ha) states that the average bowling score is less than 168 points.
To test this hypothesis, Jamie uses a significance level of 1%. The sample data consists of 17 games, with a mean score of 155 points and a standard deviation of 19 points.
To perform the hypothesis test, Jamie can use a one-sample t-test because the population standard deviation is unknown. The test statistic can be calculated as (sample mean - hypothesized mean) / (sample standard deviation / √sample size).
Substituting the given values, the test statistic is (-13) / (19 / √17) ≈ -3.02.
With 16 degrees of freedom (sample size - 1), Jamie can compare this test statistic to the critical t-value at a 1% significance level. If the test statistic falls within the critical region, Jamie can reject the null hypothesis and conclude that her bowling score is significantly less than 168 points on average.
For more similar questions on hypothesis test
brainly.com/question/4232174
#SPJ8
how would you solve this equation?

Answers
Answer:
19,188
Step-by-step explanation:
hope this helps ;)
2x - 5(-x+ 6) = 12 step by step answer pls?
Answers
Answer:
6
Step-by-step explanation:
Answer:
X is Equal 6 X=6 de nadixs
In circle C. r = 32 units.
What is the area of circle C?
A
32īt units?
c
641 units?
256TI units
1024Tt units?
Answers
Answer:
1024 pi
Step-by-step explanation:
r = 32 units.
Area = pi * r^2
Area = 3.14 * 32^2
Area = 1024 * pi
Tt = pi??
help me with this pleaseee

Answers
Answer:
41
Step-by-step explanation:
Answer:
41
Step-by-step explanation:
angle 7 and angle 4 are corresponding angles.
corresponding angles are equal
∠7 = ∠4
∠7 = 41
41 = ∠4
find and sketch the domain of the function. f(x,y)= sqrt (y) + sqrt [25-(x^2)-(y^2)]
Answers
The domain of the function is a semicircle with a radius of 5 and centered at the origin, where y is non-negative.
The domain of a function is the set of all possible input values for which the function is defined. In this case, the function is defined as:
\(f(x,y) = \sqrt{y} + \sqrt{[25 - x^2 - y^2} ]\)
To find the domain of this function, we need to determine the values of x and y that would result in the function producing a real-valued output.
For the square root of y to be real, y must be non-negative. That is, y ≥ 0.
For the square root of [\(25 - x^2 - y^2\)] to be real, we must have:
\(25 - x^2 - y^2 \geq 0\\x^2 + y^2 \leq 25\)
This is the equation of a circle with radius 5 centered at the origin. Therefore, the domain of the function is the set of all points (x, y) that lie inside or on this circle and have y ≥ 0.
In interval notation, we can write:
Domain: {(x, y) |\(x^2 + y^2 \leq 25, y \geq 0\)}
To sketch the domain, we can plot the circle with radius 5 centered at the origin and shade the region above the x-axis. This represents all the valid input values for the function. The boundary of the domain is the circle, and the domain includes all points inside the circle and on the circle itself, but not outside the circle.
For more such questions on function visit:
https://brainly.com/question/11624077
#SPJ11