Answers
Answer:
The answer is c 1, 7/15
Answer: 1 7/15
Step-by-step explanation:
did this
Related Questions
what is 37 percent of 59052
Answers
Answer:21,849.24
Step-by-step explanation:
You have a lead ball with a mass of 420 g. The density of lead is 10.5 g/cm square. What is the volume of the ball?
Answers
Answer: Volume = 40 cm3
Step-by-step explanation:
The following selected information was extracted from the records of B Solomon.
1. B Solomon, the owner of Solomon Traders, bought a new Machine for R250 000 on 1 July 2013.
2. On 1 October 2014, he purchased a second Machine for R350 000 cash.
3. On 30 June 2015, the Machine bought during 2013 was sold for R120 000 cash.
4. It is the business’ policy to depreciate Machines at 20% per annum on cost.
REQUIRED:
Prepare the following ledger accounts reflecting all applicable entries, in the books of Solomon Traders, properly balanced/closed off, for the years ended 31 March 2016:
1.1. Accumulated depreciation.
1.2. A Machines realisation.
NB: Show all calculations as marks will be awarded for calculations.
Answers
1.1. Accumulated depreciation:
The accumulated depreciation for the machine bought on 1 July 2013 would be R150,000 as of 31 March 2016.
1.2. Machine realization:
The machine bought in 2013 was sold for R120,000 on 30 June 2015, resulting in a profit/loss on the sale of R10,000.
1.1. Accumulated Depreciation:
To calculate the accumulated depreciation, we need to determine the annual depreciation expense for each machine and then accumulate it over the years.
Machine bought on 1 July 2013:
Cost: R250,000
Depreciation rate: 20% per annum on cost
Depreciation expense for the year ended 31 March 2014: 20% of R250,000 = R50,000
Depreciation expense for the year ended 31 March 2015: 20% of R250,000 = R50,000
Depreciation expense for the year ended 31 March 2016: 20% of R250,000 = R50,000
Accumulated depreciation for the machine bought on 1 July 2013:
As of 31 March 2014: R50,000
As of 31 March 2015: R100,000
As of 31 March 2016: R150,000
1.2. Machine Realisation:
To record the sale of the machine bought in 2013, we need to adjust the machine's value and the accumulated depreciation.
Machine's original cost: R250,000
Accumulated depreciation as of 30 June 2015: R100,000
Net book value as of 30 June 2015:
R250,000 - R100,000 = R150,000.
On 30 June 2015, the machine was sold for R120,000.
Realisation amount: R120,000
To record the sale:
Debit Cash: R120,000
Debit Accumulated Depreciation: R100,000
Credit Machine: R250,000
Credit Machine Realisation: R120,000
Credit Profit/Loss on Sale of Machine: R10,000 (difference between net book value and realisation amount).
These entries will reflect the appropriate balances in the ledger accounts and properly close off the accounts for the years ended 31 March 2016.
For similar question on depreciation.
https://brainly.com/question/15998639
#SPJ8
From A to Z BU
9 Love From A to Z
9 Love From A to Z
20
The
equation d = n²-12n + 43
models the number of defective
items d
produced in a manufacturing process where there
workers in a restricted
are n
area
a) solve for
When
do 30
I
b) solve for n
when
d=20
Answers
Answer:
a) we get value of n: n=10.7 or n=1.2 when d=30
b) we get value of n: n=9.6 or n=2.3 when d=20
Step-by-step explanation:
a) solve for n When do= 30
Put d= 30 in the given equation:
\(d = n^2-12n + 43\)
\(30=n^2-12n+43\\n^2-12n+43-30=0\\n^2-12n+13=0\\\)
Now, we will find value of n by using quadratic formula: \(x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)
We have a=1, b=-12 and c=13
\(n=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\n=\frac{-(-12)\pm\sqrt{(-12)^2-4(1)(13)}}{2(1)}\\n=\frac{12\pm\sqrt{144-52}}{2}\\n=\frac{12\pm\sqrt{92}}{2}\\n=\frac{12\pm9.59}{2}\\n=\frac{12+9.59}{2} , n=\frac{12-9.59}{2}\\n=10.7 , n=1.2\\\)
So, we get value of n: n=10.7 or n=1.2
b) solve for n when d=20
\(d=n^2-12n+43\\20=n^2-12n+43\\n^2-12n+43-20=0\\n^2-12n+23=0\\\)
Now, we will find value of n by using quadratic formula: \(x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\)
We have a=1, b=-12 and c=23
\(n=\frac{-b\pm\sqrt{b^2-4ac}}{2a}\\n=\frac{-(-12)\pm\sqrt{(-12)^2-4(1)(23)}}{2(1)}\\n=\frac{12\pm\sqrt{144-92}}{2}\\n=\frac{12\pm\sqrt{52}}{2}\\n=\frac{12\pm7.21}{2}\\n=\frac{12+7.21}{2} , n=\frac{12-7.21}{2}\\n=9.6 , n=2.3\\\)
So, we get value of n: n=9.6 or n=2.3
A rubber bouncy ball is dropped from a
height of 101.00 inches onto a hard flat
floor. After each bounce, the ball returns
to a height that is 19% less than the
previous maximum height. What is the
maximum height reached after the 5th
bounce?
Answers
Using a geometric sequence, it is found that the maximum height reached after the 5th bounce is of 43.48 feet.
What is a geometric sequence?A geometric sequence is a sequence in which the result of the division of consecutive terms is always the same, called common ratio q.
The nth term of a geometric sequence is given by:
\(a_n = a_1q^{n-1}\)
In which \(a_1\) is the first term.
In this problem, the ball is dropped from a height of 101.00 inches onto a hard flat floor, and after each bounce, the height is 19% less, that is, 81% of the previous height, hence the first term and the common ratio are given by:
\(a_1 = 101, q = 0.81\)
Then, the height of the nth bounce is given by:
\(a_n = 101(0.81)^{n-1}\)
And the height of the 5th bounce is:
\(a_5 = 101(0.81)^{5-1} = 43.48\)
The maximum height reached after the 5th bounce is of 43.48 feet.
More can be learned about geometric sequences at https://brainly.com/question/11847927
#SPJ1
bru,h does anyone know this?

Answers
Answer:
The width is 410ft and the length is 780ft
pleas help ill give brainiest
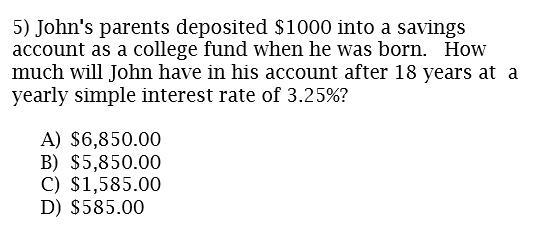
Answers
Given:
Initial amount in the account = $1,000
Interest rate = 3.25%
Since the type of interest is simple, 3.25 % of 1000 will be added to that account every year with no increase in the incrementing amount
Amount increased in 18 years:
Amount increased every year = 3.25 * 1000 / 100 = $32.5
Amount increased in 18 years = amount gained in 1 year * 18
Amount increased in 18 years = 32.5 * 18 = $585
Total amount in John's bank account at the age of 18:
Initial amount + amount increased in 18 years
1000 + 585
$1,585
First correct answer gets brainliest
Given a line with slope = -4 and y-int= (0, 5), write the equation of the line.
Writing the equation algebraically.
Answers
Answer:
\(y=-4x+5\)
Step-by-step explanation:
The equation of a line with slope \(m\) and \(y\)-intercept \((0,b)\) is \(y=mx+b\).
you sailed 0.032 units to the left and found treasure at 0.248 units find where the ship started
Answers
Pls help extra points

Answers
Please help I need this will give 100 points please help

Answers
The solution to the inequality f(x²-2) < f(7x-8) over D₁ = (-∞, 2) is:
-∞ < x < 1 or 1 < x < 6 or 6 < x < 2
Solving Inequality in a given domainGiven the inequality,
f(x²-2) < f(7x-8) over D₁ = (-∞, 2)
We need to find the values of x that satisfy this inequality.
Since we know that f is increasing over its domain, we can compare the values inside the function to determine the values of x that satisfy the inequality.
First, we can find the values of x that make the expressions inside the function equal:
x² - 2 = 7x - 8
Simplifying, we get:
x² - 7x + 6 = 0
Factoring, we get:
(x - 6)(x - 1) = 0
So the values of x that make the expressions inside the function equal are x = 6 and x = 1.
We can use these values to divide the domain (-∞, 2) into three intervals:
-∞ < x < 1, 1 < x < 6, and 6 < x < 2.
We can choose a test point in each interval and evaluate
f(x² - 2) and f(7x - 8) at that point. If f(x² - 2) < f(7x - 8) for that test point, then the inequality holds for that interval. Otherwise, it does not.
Let's choose -1, 3, and 7 as our test points.
When x = -1, we have:
f((-1)² - 2) = f(-1) < f(7(-1) - 8) = f(-15)
Since f is increasing, we know that f(-1) < f(-15), so the inequality holds for -∞ < x < 1.
When x = 3, we have:
f((3)² - 2) = f(7) < f(7(3) - 8) = f(13)
Since f is increasing, we know that f(7) < f(13), so the inequality holds for 1 < x < 6.
When x = 7, we have:
f((7)² - 2) = f(47) < f(7(7) - 8) = f(41)
Since f is increasing, we know that f(47) < f(41), so the inequality holds for 6 < x < 2.
Therefore, the solution to the inequality f(x²-2) < f(7x-8) over D₁ = (-∞, 2) is:
-∞ < x < 1 or 1 < x < 6 or 6 < x < 2
Learn more about inequality here:
https://brainly.com/question/25944814
#SPJ1
5x-3(-5y+6x) +4y i need help please
Answers
To simplify the expression \(\displaystyle\sf 5x-3(-5y+6x)+4y\), we can follow the order of operations, which involves simplifying the expressions within parentheses, applying the distributive property, and combining like terms.
Using \(\displaystyle\sf \) tags for formatting, the expression becomes:
\(\displaystyle\sf 5x-3(-5y+6x)+4y\)
First, we simplify the expression within the parentheses:
\(\displaystyle\sf 5x-3(-5y+6x)+4y\)
\(\displaystyle\sf 5x+15y-18x+4y\)
Next, we can combine the like terms:
\(\displaystyle\sf 5x-18x+15y+4y\)
\(\displaystyle\sf -13x+19y\)
Therefore, the simplified expression is \(\displaystyle\sf -13x+19y\).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
4/5 decreased by 3/5%
Answers
Answer:
Step-by-step explanation:
words algebraic symbols reason
two decreased by a number 2 - x start with 2, make it smaller
a number decreased by two x - 2 start with a number, make it smaller
two less than a number x - 2 start with a number, make it smaller
four more than a number x + 4 or 4 + x start with a number, add 4
the difference between 6 and a number 6 - x subtract, starting with 6
subtract four from a number x - 4 starting with a number, subtract 4
the sum of 4 and a number x + 4 or 4 + x add to get a sum
the opposite of the sum of a number and three -(x+3) or -(3+x) take sum, take opposite of sum
It may be convenient for the reader to use the technique the author used in writing the reason column.
Think of the word expression as a task to be completed by a computation.
Determine the operations needed.
Think how one would start and, then
think of what would need to be done to complete the task described.
Notice the uses of the preposition "of" in the last example. Prepositional phrases break up the expressions into pieces. Those beginning with "of" are discussed on the last page.
Below, notice how the prepositional phrases, in blue, which begin with by, between, from, and than, make it easier to examine the phrase and determine where to start and what to do.
words algebraic symbols reason
two decreased by a number 2 - x start with 2, make it smaller
a number decreased by two x - 2 start with a number, make it smaller
two less than a number x - 2 start with a number, make it smaller
four more than a number x + 4 or 4 + x start with a number, add 4
the difference between 6 and a number 6 - x subtract, starting with 6
subtract four from a number x - 4 starting with a number, subtract 4
the sum of 4 and a number x + 4 or 4 + x add to get a sum
the opposite of the sum of a number and three -(x+3) or -(3+x) take sum, take opposite of sum
Additional information is found in a prepositional phrases. The preposition "from" is almost always a tip-off that subtraction is required. Often, the desired mathematical expression starts with what is in the "from" prepositional phrase.
Multiplication & Division
Here are words associated with multiplication or division. The context is the key to the symbols needed, not the word itself. Remember, the word AND is a signal that there are two or more ideas, not that addition is required. Remember, to use prepositional and other phrases to break up the expression in order to determine what is required. Examples follow the list.
divide
quotient
halve, half
third
product
double
triple
square
words algebraic symbols reason
the product of two and a number 2x or 2(x) multiply
a third of the sum of a number and two (x + 2)/3 start with the sum, take a third of it
double the difference between 6 and a number 2(6-x) start with the difference, multiply by 2
triple the sum of four, five, and a number 3(4 + 5 + x) start with the sum, multiply by 3
the value of 4 nickels 4(5) or 5+5+5+5, etc. four fives or five four times
the value of some nickels 5x multiply 5 times a number
The last example may be HARD. Use the table below to examine the reason more clearly. The value of x nickels is 5x. The value of some nickels is 5x.
number of nickels value of nickels
1 5(1) = 5
2 5(2) = 10
3 5(3) = 15
4 5(4) = 20
x 5(x) = 5x
Exercises
I. Write the expression/equation then check the answer.
Note: Your browser may print the answers with spaces that are not ment to be there.
1.) the square of five
Answers
5²
2.) the square of five subtracted from a number
Answers
x - 5²
3.) the opposite of a number
Answers
-x
4.) six less than half of a number
Answers
x/2 - 6 or .5x - 6
5.) the product of a number and four
Answers
4(x) or 4x or (4)(x)
6.) a number decreased by five
Answers
x - 5
7.) five less than a number
Answers
x - 5
8.) Ten is five less than a number.
Answers
10 = x - 5
9.) A number is less than five.
Answers
x < 5
See additional info on these.
10.) one less than a number
Answers
x - 1
11.) one less than a double a number
Answers
2x - 1
12.) the opposite of the sum of a number and 12
Answers
-(x + 12)
13.) triple a number
Answers
3x
14.) twice the sum of a number and 1
Answers
2(x + 1)
III. Complete the table. Check each answer.
words algebraic symbols
1.
Answers
one less than a number
x - 1
2. the sum of six and double a number
Answers
6 + 2x or 2x + 6
3. double the sum of six and a number
Answers
2(x + 6)
4. the sum of three consecutive integers
Answers
first + second + third
(x) + (x + 1) + (x + 2)
5. the product of 2 consecutive odd integers
Answers
(first)(second)
(x)(x + 2)
IV. Complete the table. Check each answer.
words algebraic symbols
1. one more than a number
Answers
x + 1 or 1 + x
2.
Answers
one less than a number or a number decreased by one
x - 1
3. the product of a number and 3 and a different number
Answers
3xy
4.
Answers
double a number or the product of a number and two
2x
5.
Answers
the square of a number or a number multiplied by itself
x2
What is the value of x in 2.5-0.35x=-3
Answers
Answer:
X= 110/7 or 15.7 or rounded to 16
Answer:
x=15.714285
Step-by-step explanation:
-0.35x=-3-2.5
-0.35x=-5.5
-0.35/-0.35= -5.5/0.35
X=-5.5/-0.35
X=15.714285
What is the area of a rectangle with a length of 214 inches and a width of 234 inches?
714 in²
6316 in²
4316 in²
3332 in²
Answers
Given :
The length of a rectangle is 214 inches and the width is 234 inches.⠀
To Find :
The area of the rectangle.⠀
Solution :
We know that,
\(\qquad { \pmb{ \bf{Length \times Width = Area_{(rectangle)}}}}\:\)
⠀
Now substituting the values :
\(\qquad {\dashrightarrow{ \sf{214 \: in\times 234 \: in = Area_{(rectangle)}}}}\:\)
\(\qquad {\dashrightarrow \: { { \sf{50,076 \: {in}^{2} = Area_{(rectangle)}}}}\:}
\)
⠀
Hence, The area of the rectangle is 50,076 in² .
The area of a rectangle with a length of 2 1/4 inches and a width of 2 3/4 inches is 6 3/16 in². Option C is correct.
How to find the area of a rectangle?Area of a rectangle is the product of the length of the rectangle and the width of the rectangle. It can be given as,
\(A=a\times b\)
Here, (a)is the length of the rectangle and (b) is the width of the rectangle.
The rectangle given in the problem has,
A length of 2 1/4 inches. A width of 2 3/4 inches.Thus, the area of the rectangle is,
\(A=2\dfrac{1}{4}\times2\dfrac{3}{4}\\A=\dfrac{8+1}{4}\times\dfrac{8+3}{4}\\A=\dfrac{9}{4}\times\dfrac{11}{4}\\A=\dfrac{99}{16}\\\A=\dfrac{96+3}{16}\\A=6\dfrac{3}{16}\)
Thus, the area of a rectangle with a length of 2 1/4 inches and a width of 2 3/4 inches is 6 3/16 in². Option C is correct.
Learn more about the area of rectangle here;
https://brainly.com/question/11202023
How much money should be deposited today in an account that earns 4.5% compounded monthly so that it will accumulate to $15,000 in 4 years
Answers
Answer:
P ≈ $12,654.89
Step-by-step explanation:
To calculate the amount of money that should be deposited today, we can use the formula for compound interest:
A = P(1 + r/n)^(nt)
Where:
A = the future value of the investment ($15,000 in this case)
P = the principal amount (the amount to be deposited today)
r = the annual interest rate (4.5% or 0.045 as a decimal)
n = the number of times the interest is compounded per year (monthly compounding, so n = 12)
t = the number of years (4 years in this case)
Substituting the given values into the formula, we have:
$15,000 = P(1 + 0.045/12)^(12*4)
Simplifying the equation:
$15,000 = P(1.00375)^(48)
To solve for P, we divide both sides of the equation by (1.00375)^(48):
P = $15,000 / (1.00375)^(48)
Using a calculator, we find:
P ≈ $12,654.89
Therefore, approximately $12,654.89 should be deposited today in order to accumulate to $15,000 in 4 years with a 4.5% annual interest rate compounded monthly.
Find f(-3) if f(x) = x•x
Answers
Answer:
9
Step-by-step explanation:
f(x) = x•x
f(-3) = -3*-3
f(-3)= 9
how the hell do i do it #underpressure

Answers
Answer:
8 more red counters
Step-by-step explanation:
It would make it 9:3, which, when simplified, is 3:1.
Find the value of m.

Answers
Answer:
8
Step-by-step explanation:
12-10=2
10-m=2
m=8
If these cylinders and prisms were broken into two separate groups, what would be an equivalent ratio to 8/2? i dont have much longer and btw it doesn't have a picture.
100 points?
Answers
The Equivalent ratio to 8/2 is 4/1, 24/6, 32/8 and 48/12.
We have,
Cylinder and prism.
Here we have to find the equivalent ratio to 8/2.
First simplifying the given ratio as
8/2
= (4 x 2)/2
= 4 /1
Now, some more ratios equivalent to 8/2.
1. 8/2 x 3/3 = 24/ 6
2. 8/2 x 4/4 = 32/8
3. 8/2 x 6/6= 48/12
Learn more about Ratio here:
https://brainly.com/question/13419413
#SPJ1
Petra jogs 6 miles in 42 minutes. At this rate, how long would it take her to jog 8 miles?
Answers
Distance 1 / Time 1 = Distance 2 / Time 2
Using the information given:
6 miles / 42 minutes = 8 miles / Time 2
To solve for Time 2, we can cross-multiply and then divide:
6 miles * Time 2 = 8 miles * 42 minutes
6 * Time 2 = 8 * 42
6 * Time 2 = 336
Now, we divide both sides by 6 to isolate Time 2:
Time 2 = 336 / 6
Time 2 = 56 minutes
Therefore, it would take Petra 56 minutes to jog 8 miles at the same rate.
Answer:
56 minutes
Step-by-step explanation:
We can use proportions to solve.
6 miles 8 miles
------------ = ------------------
42 minutes x minutes
Using cross products.
6x = 42 *8
Divide each side by 6
x = 42/6 * 8
x = 7*8
x = 56
In APQR, r = 4.9 cm, ZR=21° and ZP=104°. Find the length of p, to the nearest 10th
of a centimeter.
Answers
Answer:
13.3
Step-by-step explanation:
Answer:
your wrong
Step-by-step explanation:
Rewrite the following expression in logarithmic form:
2^9=512
Answers
Answer: log(2) 512= 9
Step-by-step explanation:
A P E X ;)
In logarithmic form, the expression \(2^9 = 512\) can be rewritten as follows:
\(log_{(2)}\ 512 = 9\)
As we know that the logarithmic form allows us to express the exponent as the logarithm of the base to a certain value, which in this case is 9.
To understand this, let's break down the expression.
The base of the logarithm is 2, and the result of raising 2 to the power of 9 is 512.
By taking the logarithm of 512 to the base 2, we get the exponent, which is 9.
So, in logarithmic form can be written as:
\(log_{(2)}\ 512 = 9\)
Therefore, in logarithmic form, the expression \(2^9 = 512\) can be rewritten as follows:
\(log_{(2)}\ 512 = 9\)
Learn more about the logarithmic properties here:
brainly.com/question/24211708
#SPJ2
Choose the system of inequalities that best matches the graph below.

Answers
Answer: D
Step-by-step explanation:
Hope it helps
explain all steps in detall. Incluide your final answer.. 9²+3•(9-5)²/4=
Answers
Answer: 93
Step-by-step explanation:
To solve this problem, we need to use the order of operations, or PEMDAS.
Parenthesis
Exponent
Multiply
Divide
Add
Subtract
For multiply/divide and add/subtract, you don't necessarily go in that specific order. You go from left to right, depending on what comes first. For example, if division comes before multiply, you would divide first, then multiply. Same goes for add/subtract.
9²+3×(9-5)²/4 [solve parenthesis]
9²+3×(4)²/4 [solve exponent]
81+3×16/4 [solve multiply or divide, whichever comes first]
81+12 [solve add or subtract, whichever comes first]
93
Now, we know that 93 is our final answer.
The principal interest formula I = Prt can be used to find the interest earned on an initial amount of money, called the
principal, P, given an interest rate, r, and an amount of time over which interest is accrued, t. Solve I = Prt for P when
I = $5,480, r = .04 annual interest, and t 7 years. Round your answer to the nearest hundredth.
PLEASE HELP GUYS
Answers
Answer:
1885.714
Step-by-step explanation:
I = ptr
5280 = 7×0.4×p
p = 5280/2.8
p = 1885.7
A piece of lumber 2.8 meters long weighs 24.5 kilograms. A piece 0.8 meter long is cut from
the 2.8-meter length. Determine the weight of the 0.8-meter piece.
Answers
The weight of the 0.8-meter piece is 19.6 kilograms.
We can use the ratio of length to weight to determine the weight of the 0.8-meter piece.
Let's call the weight of the 2.8-meter piece "W₁" and the weight of the 0.8-meter piece "W₂". Then we have:
W₁/2.8m = 24.5kg/1m
Solving for W₁, we get:
W₁ = (24.5kg/1m) x 2.8m = 68.6kg
Now we can use the same ratio to find W₂:
W₂/0.8m = 24.5kg/1m
Solving for W₂, we get:
W₂ = (24.5kg/1m) x 0.8m = 19.6kg
Therefore, the weight of the 0.8-meter piece is 19.6 kilograms.
To learn more on Ratios click:
https://brainly.com/question/1504221
#SPJ1
How do we find the second and the third derivative of this equation? Please help!

Answers
Answer:
\(\frac{7}{2\sqrt{2} }\)
Step-by-step explanation:
substitute 2 in for x. the square root of 2 is already in radical form
what are the classification of safety signs? (1-7)
Answers
Answer:
Mandatory, prohibition, warning, danger, fire, emergency information, and limitation are the seven types of safety signage.
Step-by-step explanation:
\(5^{2} - [10* {5-3}]\)
Answers
Answer:
-22
Step-by-step explanation:
\(1. \: 5 {}^{2} - (50 - 3) \\ 2. \: 5 {}^{2} - 47 \\ 3. \: 25 - 47 \\ 4. \: - 22\)
