# I want answer in C++.
Consider two fractions in the form \( a / b \) and \( c / d \), where \( a, b, c \), and \( d \) are integers. Given a string describing an arithmetic expression that sums these two fractions in the f
Answers
To solve the fraction addition problem in C++, you can define a Fraction struct to represent fractions. Implement a gcd function to find the greatest common divisor.
Parse the input fractions and perform the addition using overloaded operators. Print the result. The code reads the input string, finds the "+" operator position, parses the fractions, performs the addition, and prints the sum.
Learn more about C++
https://brainly.com/question/9022049
#SPJ11
Related Questions
Alexis sells stuffed animals. She sells a stuffed elephant for $14.95, and the sales tax is 5% of the sale price. About how much is the sales tax on the elephant? Must show work please hurry.
Answers
Answer:
$0.75Step-by-step explanation:
Given:
Selling price is $14.95Sales tax is 5%Find the amount of the tax:
14.95*5/100 = 0.7475 ≈ 0.75 (rounded)Describe and correct the error in setting up the trigonometric function.

Answers
The value of side length w is 13.75 .
Given right angled triangle,
Perpendicular = w
Hypotenuse = 17
Angle of triangle = 54°
So,
According to the trigonometric ratios,
tanФ = p/b
cosФ = b/h
sinФ = p/h
By using sinФ,
sinФ = p/h
sin 54° = w/ 17
0.809 = w/17
w = 13.75 .
Thus after correction w will be 13.75
Know more about trigonometry,
https://brainly.com/question/25618616
#SPJ1
Can you help me with this problem?
In the equation for the time-dependent wave function Ψ(x,t)=ψ(x)e^-iωt=Ae^i(kx-ωt)+Be^-i(kx+ωt) keep both terms, putting A = B = ψ0. The equation then describes the superposition of two matter waves of equal amplitude, traveling in opposite directions. (Recall that this is the condition for a standing wave.) (a) Find |Ψ(x, t)|2. (b) Find the positions of the nodes of this standing wave in terms of λ, the de Broglie wavelength of the particle. (c) Find a similar expression for the most probable locations of the particle.
Answers
The problem deals with finding the wave function and its properties of a superposition of two matter waves of equal amplitude, traveling in opposite directions.
We are required to find the probability density function, positions of the nodes of the standing wave, and the most probable locations of the particle. (a) The probability density function is given by |Ψ(x,t)|^2=4|ψ0|^2cos^2(kx-ωt). Since A=B=ψ0, we can simplify it as |Ψ(x,t)|^2=4|ψ0|^2cos^2(kx-ωt) (b) The positions of the nodes are the positions where the probability density function is equal to zero. In this case, the probability density function is zero whenever cos^2(kx-ωt)=0. This occurs when kx-ωt=nπ/2, where n is an integer. Solving for x, we get x=(nλ/2)+(λ/4). (c) The most probable location of the particle is where the probability density function is maximum. The maximum value of the probability density function is 4|ψ0|^2. Thus, the most probable location is where cos^2(kx-ωt)=1, which occurs when kx-ωt=nπ, where n is an integer. Solving for x, we get x=nλ/2.
Learn more about amplitude here:
https://brainly.com/question/9525052
#SPJ11
The measures of two supplementary angles are ( 2x-11 )° and ( 3x+1 )°. Find the value of x.
Answers
5x - 10 = 180
5x = 190
x = 38
© Solve the simultaneous equations
-3x + y= – 8
3x + 2y = – 13
X =?
y =?
Answers
Answer:
x=1/3
y=-7
Step-by-step explanation:
using the elimination method, you can add both equations vertically, to eliminate the x
-3x+y=-8
3x+2y=-13
3y=-21
y=-7
we then fix the value of y into the first equation
-3x+y=-8
-3x-7=-8
-3x=-8+7
-3x=-1
x=1/3
If F(n) = -n Then F(-6)= ?
Answers
Answer: 6
Step-by-step explanation:
-n plug -6 in so -(-6)=6
Answer:
boo ba loob
Step-by-step explanation:
sweating in saucy bbq sauce
50% of 70
Help!! It's due by 10:00pm!!
Answers
Answer:
35
Step-by-step explanation:
35
What is 50 percent (calculated percentage %) of number 70? Answer: 35.
Answer:
50%×70
REMOVE PERCENT BY DIVIDING WITH 100
=50/100×70
=0.5×70
=35 ANSWER
Lush Gardens Co. bought a new truck for $50,000. It paid $6,000 of this amount as a down payment and financed the balance at 4.80% compounded semi-annually. If the company makes payments of $1,500 at the end of every month, how long will it take to settle the loan?
Answers
Answer:
To calculate the time it will take to settle the loan, we need to consider the monthly payments and the interest rate. Let's break down the steps:
1. Loan amount: The loan amount is the purchase price minus the down payment:
Loan amount = $50,000 - $6,000 = $44,000
2. Calculate the monthly interest rate: The annual interest rate of 4.80% compounded semi-annually needs to be converted to a monthly rate. Since interest is compounded semi-annually, we have 2 compounding periods in a year.
Monthly interest rate = (1 + annual interest rate/2)^(1/6) - 1
Monthly interest rate = (1 + 0.0480/2)^(1/6) - 1 = 0.03937
3. Calculate the number of months needed to settle the loan using the monthly payment and interest rate. We can use the formula for the number of months needed to pay off a loan:
n = -log(1 - r * P / M) / log(1 + r),
where:
n = number of periods (months),
r = monthly interest rate,
P = loan amount,
M = monthly payment.
Plugging in the values:
n = -log(1 - 0.03937 * $44,000 / $1,500) / log(1 + 0.03937)
Calculating this expression, we find:
n ≈ 30.29
Therefore, it will take approximately 30.29 months to settle the loan.
Hope it helps!
Which is a complete list of each term of each term in the expression 15 + 20x?
A. 15: 1, 3, 5, 15
20x: 1, 2, 4, 5, 10, 20, x
B. 15: 1, 3, 5, 15
20x: 1, 2, 4, 5, 10, 20
C. 15: 3, 5
20x: 4, 5, x
D. 15: 1, 3, 5
20x: 1, 2, 4, 5, 10, x
Answers
Answer:
A. 15: 1, 3, 5, 15
20x: 1, 2, 4, 5, 10, 20, x
Step-by-step explanation:
Consider the following utility function U(x,y)=X2/3Y4/5 가 Find expressions for marginal utilities of Find an expression for the marginal rate of substitution (MRSxy) 2. Describe the indifference curves associated with two goods that are perfect substitutes. What if the two goods are complements?
Answers
1. Marginal utilities:
To find the marginal utility of x (MUx), we take the partial derivative of the utility function with respect to x. In this case, MUx = (2/3)X^(-1/3)Y^(4/5).
To find the marginal utility of y (MUy), we take the partial derivative of the utility function with respect to y. In this case, MUy = (4/5)X^(2/3)Y^(-1/5).
2. Marginal rate of substitution (MRSxy):
The MRSxy represents the rate at which a consumer is willing to trade one good (x) for another good (y) while maintaining the same level of satisfaction. Mathematically, MRSxy is equal to the ratio of the marginal utilities: MRSxy = MUx/MUy.
Substituting the expressions for MUx and MUy derived earlier, we have MRSxy = [(2/3)X^(-1/3)Y^(4/5)] / [(4/5)X^(2/3)Y^(-1/5)].
Simplifying the expression, we get MRSxy = (5/6) * [(X/Y)^(1/3) * (Y/X)^(1/5)].
Thus, the expression for the marginal rate of substitution (MRSxy) is (5/6) * [(X/Y)^(1/3) * (Y/X)^(1/5)].
3. Indifference curves for perfect substitutes:
When two goods are perfect substitutes, it means that the consumer is equally satisfied with any combination of the two goods, as long as the ratio between them remains constant. In this case, the indifference curves would be straight lines with a constant slope.
For example, if the two goods are apples and oranges, and the consumer is equally satisfied with any combination of these two goods, the indifference curves would be straight lines with a constant slope of -1. This means that the consumer is willing to give up one apple for one orange and vice versa, without any change in satisfaction.
4. Indifference curves for complements:
When two goods are complements, it means that the consumer's satisfaction is maximized when the goods are consumed together in fixed proportions. In this case, the indifference curves would be L-shaped or right angles.
For example, if the two goods are coffee and sugar, and the consumer's satisfaction is maximized when the coffee and sugar are consumed together in a fixed proportion, the indifference curves would be L-shaped. This means that the consumer does not derive any satisfaction from consuming only coffee or only sugar, but rather from consuming them together in the right proportion.
Know more about Marginal utilities:
https://brainly.com/question/30841513
#SPJ11
The price of a baseball glove is $8 more than half the price of spikes. The glove costs $54. Solve the equation 5/2+ 8 = 54 to find out how much the spikes cost.
Answers
Answer:
$23
Step-by-step explanation:
1/2 + 8 = 54
subtract 8 from both sides: 1/2 = 46
divide 46 by 1/2: 23
check your answer: 23 * 2 + 8= 54
I hope this helped, please mark Brainliest, thank you!
Which is reflex angle
a.180° b.280° c.270°
Answers
Answer:
b)280° and c) 270°
A reflex angle is an angle which is more than 180° but less than 360°
If my answer helped, kindly mark me as the brainliest!!
Thank You!!
Step-by-step explanation:
180 is reflex angle.
hope it's helpful
One day 1 2 tried to make a pie. Unfortunately, she only had 3, and no sugar, so she decided to use 4 to sweeten it. The pie bubbled over in the oven and looked a mess. Not one to be discouraged, she decided to remedy the situation by covering the pie with 5 . When her 6 came over, and saw what she'd done, they 7 because 8 her pie ended up 9 but the 10 still needs to be cleaned
Answers
Answer:
even though there's no options or context,most likely answers are 1.little
2.Suzzy
3. flour
4.molases
5.foil
6 aunt
7. ate
8.
9.good
10.kitchen
in a right triangle the sine of an angle and the cosine of the same angle is what is the tangent of the angle
Answers
The tangent of the angle in a right triangle is:
Tangent = Sine / Cosine
In a right triangle, the sine of an angle is equal to the length of the side opposite the angle divided by the length of the hypotenuse. The cosine of the same angle is equal to the length of the side adjacent to the angle divided by the length of the hypotenuse.
To find the tangent of the angle, you can use the formula:
Tangent = Opposite / Adjacent
Since the opposite side is the side opposite the angle and the adjacent side is the side adjacent to the angle, the tangent of the angle can be calculated by dividing the sine of the angle by the cosine of the angle.
Therefore, the tangent of the angle in a right triangle is:
Tangent = Sine / Cosine
Know more about adjacent side here:
https://brainly.com/question/11977225
#SPJ11
The an equation of a line parallel to:
y - 1 = -3(x - 2)
in slope-intercept form
Answers
An equation of a line parallel to y - 1 = -3(x - 2) in slope-intercept form is y = -3x + 10.
What is the point-slope form?Mathematically, the point-slope form of a straight line can be calculated by using this mathematical expression:
y - y₁ = m(x - x₁)
Where:
m represents the slope.x and y represents the data points.What is the slope-intercept form?In Mathematics, the slope-intercept form of a line can be calculated by using this linear equation:
y = mx + c
Where:
x and y represents the data points.m represents the slope of a line.c represents the y-intercept of a line.Making y the subject of formula, we have:
y - 1 = -3(x - 2)
y - 1 = -3x + 6
y = -3x + 6 - 1
y = -3x + 5
Therefore, y = -3x + 10 is a possible equation of a line.
Read more on slope here: brainly.com/question/3493733
#SPJ1

The transfer function G (s): (6s³ +s² +3s-20)/ (2s4+7s³+15s²+16s+10)
Find the discrete time representation of the system at T = 0.1 and check whether the discrete system is (i) BIBO stable (ii) Asymptotic or marginally stable (iii) controllable and (iv)observable.
Answers
The discrete-time representation of the system at T = 0.1 is given by the ratio of two polynomials, where the numerator and denominator coefficients are determined using the bilinear transform. The BIBO stability and stability nature (asymptotic or marginal) cannot be determined without the pole locations in the z-plane.
To obtain the discrete-time representation of the system at T = 0.1, we can use the bilinear transform method. The bilinear transform maps the s-domain to the z-domain using the equation: \(s = (2/T)((z-1)/(z+1))\).
First, let's apply the bilinear transform to the given transfer function G(s):
\(G(z) = G(s)|s=(2/T)((z-1)/(z+1))\)
Substituting the transfer function \(G(s) = (6s^3 + s^2 + 3s - 20)/(2s*4 + 7s^3 + 15s^2 + 16s + 10)\), we have:
\(G(z) = [(6((2/T)((z-1)/(z+1)))^3 + ((2/T)((z-1)/(z+1)))^2 + 3((2/T)((z-1)/(z+1))) - 20)] / [2((2/T)((z-1)/(z+1)))^4 + 7((2/T)((z-1)/(z+1)))^3 + 15((2/T)((z-1)/(z+1)))^2 + 16((2/T)((z-1)/(z+1))) + 10]\)
Simplifying the expression, we have:
\(G(z) = [(6(2/T)^3((z-1)^3/(z+1)^3) + (2/T)^2((z-1)^2/(z+1)^2) + 3(2/T)((z-1)/(z+1)) - 20] / [2(2/T)^4((z-1)^4/(z+1)^4) + 7(2/T)^4((z-1)^3/(z+1)^3) + 15(2/T)^2((z-1)^2/(z+1)^2) + 16(2/T)((z-1)/(z+1)) + 10]\)
Simplifying further, we obtain the discrete-time representation of the system:
\(G(z) = [c_0z^4+ c_1z^3+ c_2z^2 + c_3z + c_4] / [d_0z^4+ d_1z^3 + d_2z^2 + d_3z + d_4]\)
where:
\(c_0 = (6(2/T)^3 + 2(2/T)^2 + 3(2/T) - 20)\\c_1 = (-3(6(2/T)^3+ 2(2/T)^2) + 16(2/T))\\c_2 = (3(6(2/T)^3) - 15(2/T)^2)\\c_3 = (-6(2/T)^3 + 7(2/T)^3)\\c_4 = 2(2/T)^4\\d_0 = 2(2/T)^4\\d_1 = 7(2/T)^4 + 16(2/T)\\d_2 = 15(2/T)^2\\d_3 = -6(2/T)^2\\d4 = 10\)
Now, let's analyze the properties of the discrete system:
(i) BIBO Stability:
To determine if the discrete-time system is BIBO stable, we need to check if all the poles of the transfer function G(z) lie inside the unit circle in the z-plane. If all poles are inside the unit circle, the system is BIBO stable.
(ii) Asymptotic or Marginally Stable:
By analyzing the pole locations of the discrete system, we can determine if it is asymptotically stable (all poles inside the unit circle) or marginally stable (some poles on the unit circle).
(iii) Controllability:
The controllability of the discrete system can be assessed by examining the controllability matrix based on the system's state-space representation. Unfortunately, without the state-space representation, it is not possible to determine controllability.
(iv) Observability:
The observability of the discrete system can be determined by examining the observability matrix based on the system's state-space representation. However, without the state-space representation, it is not possible to determine observability.
To fully analyze the discrete system, we would need the state-space representation or further information. However, we can still determine the BIBO stability and stability nature (asymptotic or marginal) based on the pole locations in the z-plane.
Learn more about the bilinear transform here:
https://brainly.com/question/15310052
#SPJ4
help pleaseeee i dont get this also show work

Answers
Answer:
AC = 2
BC = \(2\sqrt{2}\)
CD = 4
CF = 4
BD = \(2\sqrt{2}\)
DE = 8
EF = \(4\sqrt{2}\)
DF = \(4\sqrt{2}\)
Step-by-step explanation:
Since all of these are isosceles triangles, it means both legs of every triangle are congruent to each other. So,
Given: AB = 2
Find:
AC = AB = 2
BC = \(2\sqrt{2}\)
CD = 4
CF = CD = 4
BD = BC = \(2\sqrt{2}\)
DE = 8
EF = \(4\sqrt{2}\)
DF = EF = \(4\sqrt{2}\)
.Complete the pattern: 5,7,4,6,3,5,____
Answers
Answer:
2
Step-by-step explanation:
You add 2 subtract 3
Answer:
its 2, you add 2 then subtract 3
Step-by-step explanation:
Find the area of a lateral face of the regular pyramid.

Answers
Answer:
2684 \(units^{2}\)
Step-by-step explanation:
We find the area of the 4 triangles
area = 1/2 base x height All the bases area the same measurement
a = 1/2(22)(61)
a = 671
There are 4 sides
671 x 4 = 2684
Calculate the 95% confidence interval for the following fictional data regarding daily TV viewing habits: µ= 4.7 hours; σ= 1.3 hours; sample of 78 people, with a mean of 4.1 hours.
Answers
We can be 95% confident that the true population mean TV viewing time is between 3.812 and 4.388 hours.
To calculate the 95% confidence interval, we use the formula:
CI = x' ± Zα/2 * (σ/√n)
Where:
x' = sample mean
Zα/2 = the Z-score associated with the desired confidence level (in this case, 95%, so Zα/2 = 1.96)
σ = population standard deviation
n = sample size
Substituting the given values, we get:
CI = 4.1 ± 1.96 * (1.3/√78)
Calculating the standard error (SE) first:
SE = σ/√n
SE = 1.3/√78
SE ≈ 0.147
Then we substitute the SE value in the CI formula:
CI = 4.1 ± 1.96 * 0.147
CI = 4.1 ± 0.288
CI = (3.812, 4.388)
To learn more about confidence interval click on,
https://brainly.com/question/13956031
#SPJ4
HELP! QUICK! NO BOTS!

Answers
Part of the population of 7,000 elk at a wildlife preserve is infected with a parasite. A random sample of 50 elk shows that 7 of them are infected. How many elk are likely to be infected?
Answers
Answer:
620
Explanation:
When the sample is given, the number of elk are likely to be infected is to be considered as the 620.
Calculation of the number of elk:
Since the population is 7,750.
The random sample is 50.
So here be like
= 620
hence, When the sample is given, the number of elk are likely to be infected is to be considered as the 620.
if 13n-6 = 98 what is the value of n
Answers
Answer:
n = 8
Step-by-step explanation:
13n-6 = 98
Solution:
13n = 98+613n = 104n = 104/13n = 8Hence the value of n is 8.
13n - 6 = 98
13n = 98 + 6
13n = 104
n = 104/13
n = 8
if the mean of a group of samples is 135 with a standard deviation of 45, what is the probability that a number would be less than 170?
Answers
Answer: C / .33
Step-by-step explanation:
hey does anyone know the answer to this?!

Answers
Answer:
the answer to your question is yes, but the answer to #21 is ;
mn
pn
ml
lp
Step-by-step explanation:
Find −9/14+2/7. Write your answer as a fraction in simplest form.
−9/14+2/7=
Answers
Answer: -5/14
Step-by-step explanation:
I did the work and I rechecked the answer.
help me please I'm stuck

Answers
If f(x) = 3x-6 and g(x) = 1/3x+1, then (g(f))^-1 (x) equals.
1-x
1/3(3x-1)
(x+1)
(x-1)
Answers
We need to find the inverse of the function gof (x). First we need to find the composite function gof (x) which is given by:
\(g(f(x)) = g(3x - 6)\)
= \((1/3)(3x - 6) + 1\)
= x - 1 + 1
= x
Thus,
gof (x) = x.
Now we need to find the inverse of the function gof (x) to obtain
\((gof)^-1 (x).\)
We have gof (x) = x
which implies\((gof)^-1 (x)\)
= gof (x)^-1
= x^-1
= 1/x,
x ≠ 0
Therefore,
\((gof)^-1 (x) = 1/x\)
which is option (3) (x+1) since 1/x can be written as 1/(x+1-1), where (x+1-1) is the denominator of 1/x.
Hence, the correct option is (3).
To know more about two functions visit:
https://brainly.com/question/19517220
#SPJ11
To find (g(f))^-1 (x), substitute the expression for f(x) into g(x) and simplify. The composition of g(f) is x and its inverse is also x. Therefore, (g(f))^-1 (x) equals x.
Explanation:To find (g(f))^-1 (x), we need to first find the composition of g(f) and then find its inverse. Start by substituting the expression for f(x) into g(x): g(f(x)) = g(3x-6) = \frac{1}{3}(3x-6) + 1 = x - 1 + 1 = x. So, g(f(x)) = x. Now, to find the inverse of g(f), we switch the x and y variables and solve for y: y = x. Therefore, (g(f))^-1 (x) = x.
Learn more about Composition of Functions here:https://brainly.com/question/33783470
#SPJ12
A drug tester claims that a drug cures a rare skin disease
73% of the time. The claim is checked by testing the drug on 100 patients. If at least 71 patients are cured the claim will be accepted.
find the probability that the claim will be rejected assuming that the manufacturer's claim is true. use the normal distribution to approximate the binomial disribution if possible.
The probability is ______ (round to four decimal places)
Answers
the probability that the claim will be rejected assuming the manufacturer's claim is true is approximately 0.2489.
To find the probability that the claim will be rejected assuming the manufacturer's claim is true, we need to calculate the probability of having 70 or fewer patients cured out of 100.
First, we need to determine the mean (μ) and standard deviation (σ) of the binomial distribution.
For a binomial distribution, the mean (μ) is given by μ = n * p, where n is the number of trials (100 patients) and p is the probability of success (0.73).
μ = 100 * 0.73 = 73
The standard deviation (σ) of a binomial distribution is given by σ = sqrt(n * p * (1 - p)).
σ = sqrt(100 * 0.73 * (1 - 0.73)) = sqrt(100 * 0.73 * 0.27) = sqrt(19.71) ≈ 4.44
Next, we will use the normal distribution to approximate the binomial distribution. Since the sample size is large (n = 100) and both np (100 * 0.73 = 73) and n(1 - p) (100 * 0.27 = 27) are greater than 5, the normal approximation is valid.
We want to find the probability of having 70 or fewer patients cured, which is equivalent to finding the cumulative probability up to 70 using the normal distribution.
Using the z-score formula:
z = (x - μ) / σ
For x = 70:
z = (70 - 73) / 4.44 ≈ -0.6767
Now, we can use a standard normal distribution table or a calculator to find the cumulative probability up to z = -0.6767.
The cumulative probability P(X ≤ 70) is approximately 0.2489.
Therefore, the probability that the claim will be rejected assuming the manufacturer's claim is true is approximately 0.2489.
Learn more about Probability here
https://brainly.com/question/32117953
#SPJ4
What is the total length of 3 pieces that are 1/4 foot long?
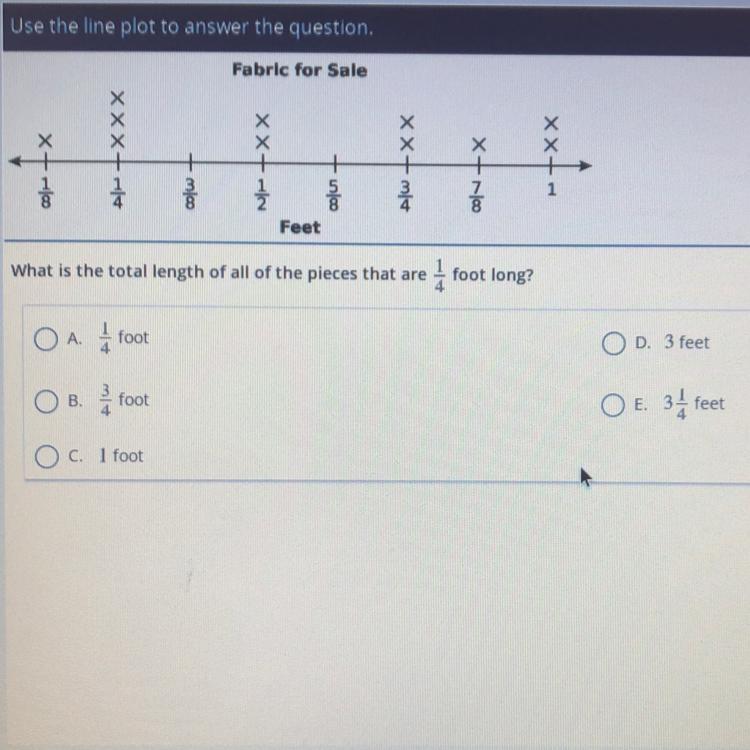
Answers
Answer:
3/4
Step-by-step explanation:
1/4 + 1/4 + 1/4 =3/4
or
1/4 x 3 = 3/4
Answer:
3/4 feet
Step-by-step explanation:
the common denominator (4) always stays the same.
you add the 3 pieces.