I want to know the process. Please write well.
The following is called one way model. €¡j N(0,02) is independent of each other. X¡j = µ¡ + €¡j i=1,2,...,m j = 1,2,...,n Find the likelihood ratio test statistic for the following hypothesis
Answers
Given a hypothesis H0: µ = µ0, the alternative hypothesis H1: µ ≠ µ0, the likelihood ratio test statistic is given by the formula:
$$LR = \frac{sup_{µ \in \Theta_1} L(x, µ)}{sup_{µ \in \Theta_0} L(x, µ)}$$
where Θ0 is the null hypothesis and Θ1 is the alternative hypothesis, L(x, µ) is the likelihood function, and sup denotes the supremum or maximum value. The denominator is the maximum likelihood estimator of µ under H0, which can be calculated as follows:
$$L_0 = L(x, \mu_0) = \prod_{i=1}^{m} \prod_{j=1}^{n} \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x_{ij}-\mu_0)^2}{2\sigma^2}} = \frac{1}{(\sqrt{2\pi}\sigma)^{mn}} e^{-\frac{mn(\bar{x}-\mu_0)^2}{2\sigma^2}}$$
where $\bar{x}$ is the sample mean. The numerator is the maximum likelihood estimator of µ under H1, which can be calculated as follows:
$$L_1 = L(x, \mu_1) = \prod_{i=1}^{m} \prod_{j=1}^{n} \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x_{ij}-\mu_1)^2}{2\sigma^2}} = \frac{1}{(\sqrt{2\pi}\sigma)^{mn}} e^{-\frac{mn(\bar{x}-\mu_1)^2}{2\sigma^2}}$$
where $\bar{x}$ is the sample mean under H0. Therefore, the likelihood ratio test statistic is given by:
$$LR = \frac{L_1}{L_0} = e^{-\frac{mn(\bar{x}-\mu_1)^2-mn(\bar{x}-\mu_0)^2}{2\sigma^2}} = e^{-\frac{mn(\bar{x}-\mu_1+\mu_0)^2}{2\sigma^2}}$$If $H_0$ is true, $\bar{x}$ follows a normal distribution with mean $\mu_0$ and variance $\frac{\sigma^2}{n}$, so the test statistic can be written as:
$$LR = e^{-\frac{m(\bar{x}-\mu_1+\mu_0)^2}{2\sigma^2/n}}$$
This follows a chi-squared distribution with 1 degree of freedom under $H_0$, so the critical region is given by:
$LR > \chi^2_{1, \alpha}$where $\chi^2_{1, \alpha}$ is the critical value from the chi-squared distribution table with 1 degree of freedom and level of significance α.
To know more about ratio refer to:
https://brainly.com/question/1375044
#SPJ11
Related Questions
Loreto quería decorar un viejo tambor metálico para usarlo de paragüero. Para ello, contaba con un grueso cordón que pretendía pegar en el contorno del borde superior del tambor. Sabiendo que el diámetro de este era 58,5 cm, cortó el cordón, dejando el trozo más largo de 175,5 cm de longitud de modo que le alcanzara justo, pero le faltaron 7 cm. ¿Cuál fue el error de Loreto?
Answers
Answer:
u should put the question in English to so English people can also help
I need help finding a, b, and c. Thank you!

Answers
a b c
Answer:
a = 1
b = 4
c = -3
1. Dennis made a 500 km trip in five hours. For the first two hours, Dennis had an average speed of 150 km/h. For the last two hours, Dennis had an average speed of 100 km/h. Which of the following is true about Dennis' trip? (25 Points) Dennis must have maintained a constant velocity throughout his trip. Dennis must have maintained a constant speed throughout his trip. O Dennis must have stopped for an hour in the middle of this trip Wich statemeent correctly discribes the locaton and Dennis must have driven without stopping during his trip
Answers
Answer:
The correct option is;
Dennis must have stopped for an hour in the middle of this trip
Step-by-step explanation:
The given parameters are;
The distance Dennis covered in 5 hours = 500 km
Dennis's average speed in the first two hours = 150 km/h
Dennis's average speed in the last two hours = 100 km/h
Therefore;
Dennis traveled 150 km/h × 2 h = 300 km in the first two hours
Dennis traveled 100 km/h × 2 h = 200 km in the last two hours
Which gives, Dennis traveled 300 km + 200 km in 2h + 2h = 4h
Therefore, Dennis traveled 500 km in 4 hours and Dennis must have stopped for an hour in the middle of this trip.
Solve for f: 7a−3d+6f=5

Answers
Divide everything by 6
F = -7a + 3d + 5 / 6
I need help with these questions
(check pictures)




Answers
Answer:
1. 920.0 after that 1830/2 after that 9.1* 10 raised to 2 after that 918%
Step-by-step explanation:
The product of b and 3 is greater than or equal to -30.
Answers
Answer:
greater than
Step-by-step explanation:
positive is higher than negative
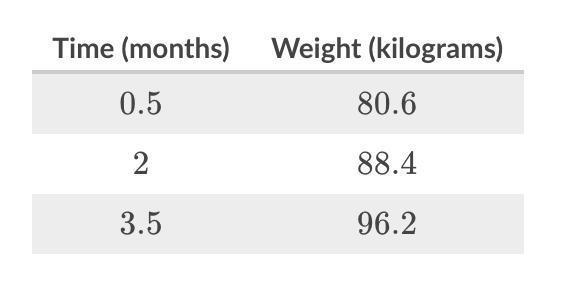
A young sumo wrestler decided to go on a special diet to gain weight rapidly. He gained weight at a constant rate.
The table compares the wrestler's weight (in kilograms) and the time since he started his diet (in months).
How fast did the wrestler gain weight?
___ kilograms per month
Answers
Finding the rate of the weight gain, we divide the total weight gained with the total number of months that took to gain that weight.
Total time (months) = 0.5 + 2 + 3.5 = 6 months
Total weight (kg) = 80.6 + 88.4 + 96.2 = 265.2 kilograms
Rate = Kg ÷ Months
Rate = 265.2 ÷ 6 = 44.2
44.2 kilograms per month
Cheers!
Answer:
78 kilograms
Step-by-step explanation:
khan told me
Solve for x in the diagram below.

Answers
180-(45+15) = 120
4x+120=180
4x=60
x=15
What is the interest you will pay if you borrowed $5,400 at 6% interest for 1 year
Answers
I dont really know how to give an explanation in detail but the answer is 32.40
5400 x .06 x 1
(turn the percent into a decimal)
The interest should be paid for 1 year is $324.
What is the Formula for Simple Interest?The formula for Simple Interest
SI = ( PRT)/100
where, P- Principal
R- Rate
T- Time
Given:
P = $5400
R= 6%
T= 1 year
So, Simple Interest
= PRT/100
= 5400 x 6 x 1 /100
= $324
Hence, the interest should be paid for 1 year is $324.
Learn more about Simple Interest here:
https://brainly.com/question/25845758
#SPJ5
Help Please really do need help

Answers
Answer:
your answer would be a whole number, so your answer would be 1,000 i think.
this should be the answer because if you multiply
9*1000 you get 9000
if you multiply
25 * 1000 you get 25000
so on and so on
Step-by-step explanation:
hope this helps :)
CAN SOMEONE PLEASE HELP, ILL GIVE BRAINLIEST.

Answers
Answer:
x = 3.5
Step-by-step explanation:
3.5 x 3 is 10.5. Triangle two has been expanded each side by 1.5. So multiply 7 (the side with 3x on the other triangle) x 1.5 to get 10.5. To fid x divide 10.5 by 3. This gives you 3.5 as x.
Hope it helps!
Answer:
x = 3.5
Step-by-step explanation:
What we know that the scale factor is 1.5 going from DEF to XYZ (4.5/3 = 1.5; 7.5/5 = 1.5)
So, multiply 7 by 1.5 to get ZX's length. It would be 10.5 units long.
We now know the equation, which is 3x = 10.5
3x = 10.5
Cancel out the multiplication by dividing both sides by 3
x = 10.5/3
Divide 10.5 by 3 to get 3.5
x = 3.5 in this case.
For this question, use the following functions.
f(x) = 2x + 6
g(x) = 4x2 – 9
Find a simplified expression for f(f(x)).
O 2x – 12
0 4x + 12
O 2x + 6
O 4x + 18
Answers
Answer:
4x + 18
Step-by-step explanation:
This is called a composite function, meaning passing the range of one function as a domain of another function.
For f(f(x)), the inner-function's range is passed as the domain of the outer function.
We can do so by substitution,
The range of f(x) can be written as 2x + 6 for any defined x values,
So we will substitute 2x + 6 as the 'x' of another function which is in this case
f(x) again, so it looks like this 2(2x+6) + 6 which can be simplified into
4x + 18
what is the equation for slope: 3 and y intercept: -8
Answers
Answer: 3
Step-by-step explanation: search there :D
In an upcoming election, 16 states will elect a new governor. Each state has only two candidates, a Democrat and a Republican, running for governor. Also, in each state, the polls indicate that each candidate is equally likely to win. Find the probabilities associated with the following events. a. Democrats win all 16 gubernatorial elections. b. Half of the elections are won by Democrats and the other half by Republicans.
Answers
a) The probability of Democrats winning all 16 elections is 1/65,536.
b) The probability of exactly half of the elections being won by Democrats and the other half by Republicans is 12870/65,536 .
a. The probability of Democrats winning all 16 gubernatorial elections, we need to determine the probability of a Democrat winning each individual election and then multiply those probabilities together since the events are independent.
Since each candidate is equally likely to win in each state, the probability of a Democrat winning an individual election is 1/2 (0.5).
Therefore, the probability of Democrats winning all 16 elections
= (1/2)¹⁶
= 1/2¹⁶
= 1/65,536.
b. The probability of half of the elections being won by Democrats and the other half by Republicans, we can use the concept of combinations. There are a total of 16 elections, and we want exactly 8 of them to be won by Democrats.
The number of ways to choose 8 elections out of 16 is given by the combination formula
C(16, 8) = 16! / (8! × (16-8)!)
= 12870.
Since each candidate is equally likely to win in each state, the probability of a Democrat winning an individual election is 1/2 (0.5). Similarly, the probability of a Republican winning an individual election is also 1/2 (0.5).
Therefore, the probability of exactly half of the elections being won by Democrats and the other half by Republicans
= (1/2)⁸ × (1/2)⁸ × 12870
= 1/2¹⁶ × 12870
= 12870/65,536.
So, the probability is 12870/65,536 or approximately 0.1967.
To know more about probability click here :
https://brainly.com/question/22478862
#SPJ4
John bought a full 1 liter bottle of soda. He drank half of it. How many milliliters of soda does John have left?
Answers
Answer:
500 ml
Step-by-step explanation:
1 liter = 1 000 ml
1 / 2 liters = 1000 ml /2 = 500 ml
1000ml - 500 ml = 500 ml
A dentist studied the number of cavities filled in all of his patients over the last three years. Let X be the number of cavities filled in the last three years for a randomly chosen patient. The dentist found that the random variable, X, had the probability distribution shown in the table. 0 1 2 3 4 Number of Cavities Probability 0.35 0.30 0.15 0.15 0.05 Let D be the difference in the number of cavities filled in two randomly selected patients. Assuming that cavities are filled independently of one another, what is the standard deviation of D? OO 0.15 1.49 1.73 2.98
Answers
To calculate the standard deviation of the difference in the number of cavities filled in two randomly selected patients, we need to determine the probability distribution for the difference and then apply the formula for standard deviation. The standard deviation of D is approximately 1.73.
To find the probability distribution for the difference D, we need to consider all possible combinations of cavities filled by two patients. We subtract the number of cavities filled in one patient from the number of cavities filled in the other patient to obtain the difference. We can create a table to represent the probability distribution of D:
Difference (D) Probability
0 0.35^2 + 0.30^2 + 0.15^2 + 0.05^2
1 2 * (0.35 * 0.30 + 0.30 * 0.15 + 0.15 * 0.05)
2 2 * (0.35 * 0.15 + 0.30 * 0.05)
3 2 * (0.35 * 0.05)
4 0
Next, we calculate the expected value (mean) of D, which is given by E(D) = Σ(D * P(D)).
Using the calculated probabilities and their corresponding differences, we find E(D) = 0 * (0.35^2 + 0.30^2 + 0.15^2 + 0.05^2) + 1 * 2 * (0.35 * 0.30 + 0.30 * 0.15 + 0.15 * 0.05) + 2 * 2 * (0.35 * 0.15 + 0.30 * 0.05) + 3 * 2 * (0.35 * 0.05) + 4 * 0 = 0.75.
Now, we calculate the variance of D using the formula Var(D) = E(D^2) - [E(D)]^2.
Substituting the values, Var(D) = 1.23 - 0.75^2 = 1.23 - 0.5625 = 0.6675.
Finally, the standard deviation of D is given by the square root of the variance, which is approximately √0.6675 ≈ 0.816.
Therefore, the standard deviation of D is approximately 1.73 (rounded to two decimal places).
Learn more about probability distribution here:
https://brainly.com/question/15930185
#SPJ11
Can someone please help me with this? Show work please.

Answers
Answer:
8 feet.
Step-by-step explanation:
Area of rectangle:Before remodeling:
width = 9 ft
Area = 108 ft²
\(\boxed{length = \dfrac{Area}{width}}\)
\(=\dfrac{108}{9}\\\\= 12 \ ft\)
After remodeling:
width = 9 ft
Area = 180 ft²
\(length = \dfrac{180}{9}\\\)
= 20 ft
length after remodeling = 20 ft
To find the length of the added portion, subtract the length of the living room before modeling from the length after remodeling.
length of the added portion = 20 - 12
= 8 ft
Are the ratios 2:1 and 18:7 equivalent?
Answers
Answer:
No
Step-by-step explanation:
The ratio of 2:1 means that the second number is half of the first number. In the ratio 18:7, 7 is not half of 18.
hope this helps!
Steven earns extra money babysitting. He charges 31.5 dollars for 5 hours and 50 dollars for 8 hours.
Answers
Money earned by Steven as per the charges 31.25 dollars for 5 hours and 50 dollars for 8 hours babysitting ,then Steven charges 18.75 dollars for 3 hours.
As given in the question,
Extra money earned by Steven by babysitting.
Charges for 5 hours babysitting is 31.25 dollars
Charges for 8 hours babysitting is 50 dollars
Charges per hour
50/8 =31.25/5 = 6.25dollars
Charges for 1 hour babysitting = 6.25 dollars
Charges for 3hour babysitting = (6.25 × 3)dollars
=18.75 dollars
Therefore, money earned by Steven as per the charges 31.25 dollars for 5 hours and 50 dollars for 8 hours babysitting ,then Steven charges 18.75 dollars for 3 hours.
The complete question is :
Steven earns extra money babysitting. He charges 31.25 dollars for 5 hours and 50 dollars for 8 hours.
How much would Steven charge for three hours?
Learn more about charges here
brainly.com/question/19886264
#SPJ1
Suppose y varies inversely with x, and y = 49 when x = 17
. What is the value of x when y = 7 ?
Answers
Answer:
119 is the value of x when y = 7
Step-by-step explanation:
Since y varies inversely with x, we can use the following equation to model this:
y = k/x, where
k is the constant of proportionality.Step 1: Find k by plugging in values:
Before we can find the value of x when y = k, we'll first need to find k, the constant of proportionality. We can find k by plugging in 49 for y and 17 for x:
Plugging in the values in the inverse variation equation gives us:
49 = k/17
Solve for k by multiplying both sides by 17:
(49 = k / 17) * 17
833 = k
Thus, the constant of proportionality (k) is 833.
Step 2: Find x when y = k by plugging in 7 for y and 833 for k in the inverse variation equation:
Plugging in the values in the inverse variation gives us:
7 = 833/x
Multiplying both sides by x gives us:
(7 = 833/x) * x
7x = 833
Dividing both sides by 7 gives us:
(7x = 833) / 7
x = 119
Thus, 119 is the value of x when y = 7.
simple length questions for grade 7 students in kenya
Answers
Answer:
what is the length of a scalec?
Step-by-step explanation:
15 or 30 mtrs
the width of a confidence interval estimate of the population mean widens when the
Answers
The width of a confidence interval estimate of the population mean widens when there is increased variability in the sample data or a lower level of confidence desired by the researcher. It is also influenced by the sample size, where larger sample sizes tend to result in narrower confidence intervals.
A confidence interval is a range of values that is likely to contain the true population mean with a certain level of confidence. The width of the confidence interval is determined by several factors. One important factor is the variability in the sample data. When there is greater variability, it means that the individual observations in the sample are spread out over a wider range. This increased spread leads to a wider confidence interval because it becomes more difficult to estimate the population mean accurately.
Another factor affecting the width of the confidence interval is the desired level of confidence. A higher level of confidence, such as 95% or 99%, requires a wider interval to provide a greater assurance of capturing the true population mean. On the other hand, a lower level of confidence, like 90%, allows for a narrower interval but with a reduced level of certainty.
Additionally, the sample size plays a crucial role in determining the width of the confidence interval. A larger sample size tends to yield a more precise estimate of the population mean, resulting in a narrower confidence interval. This is because larger samples provide more information about the population and reduce the impact of random variation in the data.
In summary, the width of a confidence interval estimate of the population mean widens when there is increased variability in the sample data or a lower level of confidence desired by the researcher. Conversely, a smaller variability, higher confidence level, and larger sample size lead to narrower confidence intervals.
Learn more about confidence interval here: brainly.com/question/32546207
#SPJ11
A train travels 300km in 6 hours. How long will it take to complete a journey of 550km? ( show working pls )
Answers
To find: time take for a train to complete a journey of 550km, hence can use the formula:
distance = speed × time
time = Speed/distance
Given,
The distance to be covered: 550km
Speed of the train is: 300km/6 hours
To find the time it will take for a train complete a journey of 550km, we can set the distance to 550km and the speed to 300km/6 hours and solve for time:
Distance = Speed * Time
550km = (300km/6 hours) × time
time = 550km / (300km/6 hours)
time = 550km * 6 hours / 300km
Answer: It will take the train 11 hours to complete a journey of 550km.
Speed- Distance concept:
https://brainly.in/question/26600085?referrer=searchResults
https://brainly.in/question/47776531?referrer=searchResults
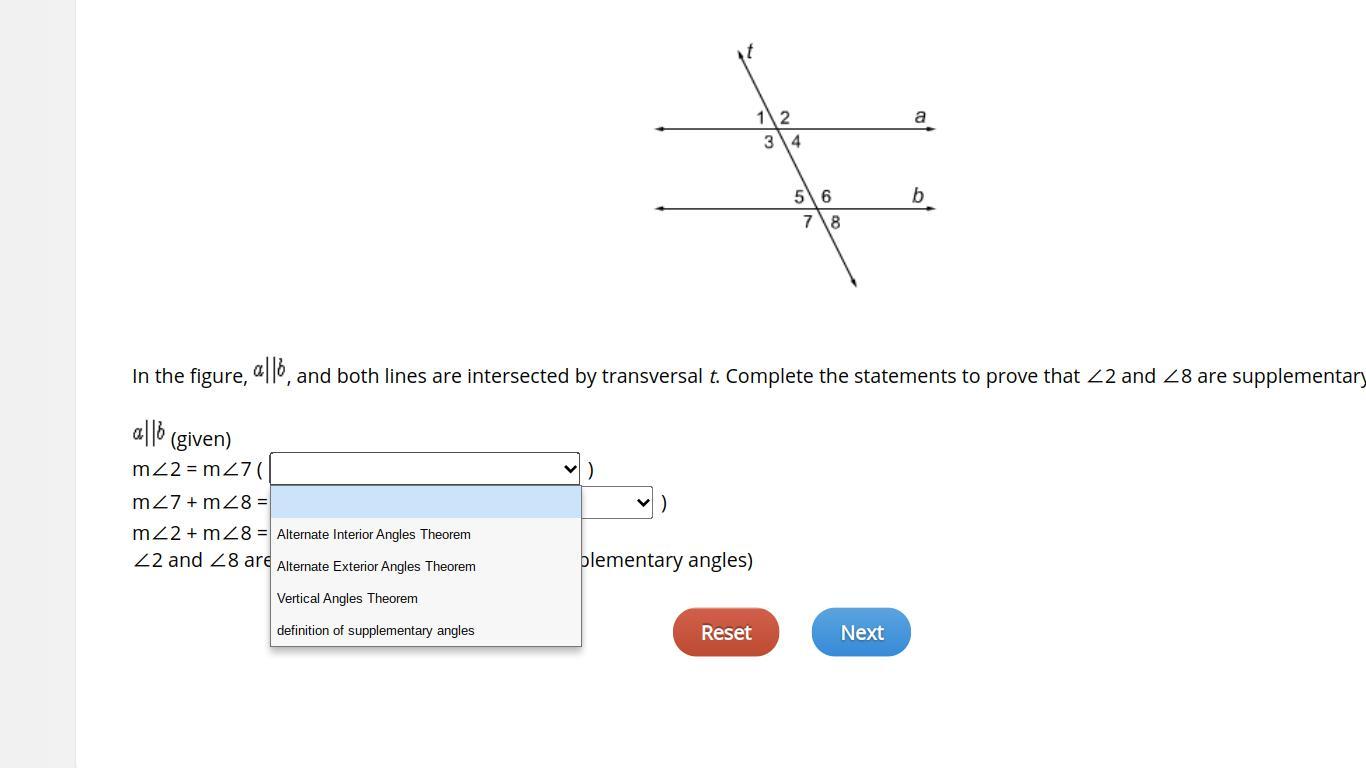
In the figure, a||b , and both lines are intersected by transversal t. Complete the statements to prove that ∠2 and ∠8 are supplementary angles.
Menu Options
m∠2 = m∠7 ( )
m∠7 + m∠8 = 180° ( )


Answers
Answer:
Step-by-step explanation:
m∠2 ≅ m∠7 [Alternate exterior angles]
m∠7 + m∠8 = 180° [Linear pair theorem]
m∠2 + m∠8 = 180° [Substitution property]
∠2 and ∠8 are supplementary [Definition of supplementary angles]
What is the solution to the equation 5x + 2(x-4)= 5x + x -10?
03
02
0-2
0-3
Answers
Answer:
5x+2x(x-4)=5x+x-10
5x+2x-8=5x+x-10
5x-5x+2x+x=-10+8
x+3x=-2
4x=-2
x=-2
The price of Stock A 9 AM was $12.71. Since then, the price has been increasing at the rate of $0.05 each hourAt noon the price of Stock 8 was \$13.46 . To decrease at the rate of by $0.12each hour. If the two rates continue, in how many hours will the prices of the two stocks be the same?
Answers
Answer:
4.4 hours
Step-by-step explanation:
Let the number of hours be represented as h
The price of Stock A 9 AM was $12.71. Since then, the price has been increasing at the rate of $0.05 each hour
$12.71 + $0.05 × h
12.71 + 0.05h
At noon the price of Stock 8 was \$13.46 . To decrease at the rate of by $0.12each hour.
$13.46 + $0.12 × h
13.46 - 0.12h
If the two rates continue, in how many hours will the prices of the two stocks be the same?
12.71 + 0.05h = 13.46 - 0.12h
0.05h + 0.12h = 13.46 - 12.71
0.17h = 0.75
h = 0.75/0.17
h = 4.41176470588 hours
Approximately = 4.4 hours
The prices of the two stocks be the same in 4.4 hours
Which expression is equivalent to 2/3(6x+3)
Answers
2/3 x 3(2x+1)
2(2x+1)
4x+2
Therefore your answer is 4x+2
rewrite the formula p=2L+2w
Answers
P=2(l+w)
Find the particular antiderivative of the following derivative that satisfies the given condition. C''(x)=4x2-3x ; C(0)=2000
Answers
The particular antiderivative that satisfies the given condition is: C(x) = (4/9)x^4 - (9/8)x^3 + K1x + 2000
To find the particular antiderivative (or integral) of the given derivative \(C''(x) = 4x^2 - 3x\) that satisfies the condition C(0) = 2000, we need to integrate the given function twice.
First, we integrate C''(x) to find C'(x):
\(C'(x) = ∫ (4x^2 - 3x) dx\)
To find the antiderivative of \(4x^2\), we use the power rule for integration: the power of x increases by 1 and is divided by the new power. Similarly, the antiderivative of -3x is \(-(3/2)x^2\).
\(C'(x) = ∫ (4x^2 - 3x) dx = (4/3)x^3 - (3/2)x^2 + K1\)
Here, K1 is the constant of integration. Next, we integrate C'(x) to find C(x):
\(C(x) = ∫ (C'(x)) dx = ∫ ((4/3)x^3 - (3/2)x^2 + K1) dx\)
To find the antiderivative of \((4/3)x^3\), we again use the power rule for integration. Similarly, the antiderivative of \(-(3/2)x^2\) is \(-(3/2)(1/3)x^3\).
The constant of integration K1 will also be integrated with respect to x, resulting in another constant of integration, K2.
\(C(x) = (1/3)(4/3)x^4 - (1/2)(3/2)x^3 + K1x + K2\)
Simplifying further, we have:
\(C(x) = (4/9)x^4 - (9/8)x^3 + K1x + K2\)
Now, we can apply the initial condition C(0) = 2000 to find the particular solution for K2:
\(C(0) = (4/9)(0)^4 - (9/8)(0)^3 + K1(0) + K2 = 2000\)
Since all the terms involving x become zero when x = 0, we have:
K2 = 2000
Therefore, the particular antiderivative that satisfies the given condition is: \(C(x) = (4/9)x^4 - (9/8)x^3 + K1x + 2000\)
To know more about antiderivative refer here:
https://brainly.com/question/33243567
#SPJ11
How is the slope related to a unit rate?
Answers
The unit rate, which is a constant between the ratio of two numbers that vary concurrently, can also be used to refer to the slope. Slope follows the same rule.
How is the slope related to a unit rate?As long as the rise/run along the line remains constant, the slope between any two places on a straight line will always be the same.
A linear relationship grows or shrinks at a constant rate of change, similar to a proportional relationship. This is known as the constant of proportionality in a relationship. It can also be referred to as the slope or unit rate in a linear connection. The slope of a line said to be its steepness.
Like the proportionality constant, the slope shows how quickly an amount is rising or falling. The only difference between the slope and the constant of proportionality is that the relationship need not begin at 0. Mathematicians frequently substitute the term slope or unit rate for the proportionality constant.
To find about the similar questions on 'unit rate', click here:
https://brainly.com/question/18047340
#SPJ2