Identify a pattern in each list of numbers. Then use this pattern to find the next number.
5, 12, 33, 96, 285, ___
Answers
=====================================================
Explanation:
The given sequence is 5, 12, 33, 96, 285, ...
The jump from 5 to 12 is +7The jump from 12 to 33 is +21The jump from 33 to 96 is +63The jump from 96 to 285 is +189The sequence of increases is: 7, 21, 63, 189
Then notice,
The jump from 7 to 21 is "times 3"The jump from 21 to 63 is also "times 3"The jump from 63 to 189 is also "times 3".Assuming this pattern keeps up, the next increment will be 189*3 = 567
We add this increment to the last term of the original sequence
285+567 = 852
The sequence is now 5, 12, 33, 96, 285, 852, ...
Related Questions
Can you please help me
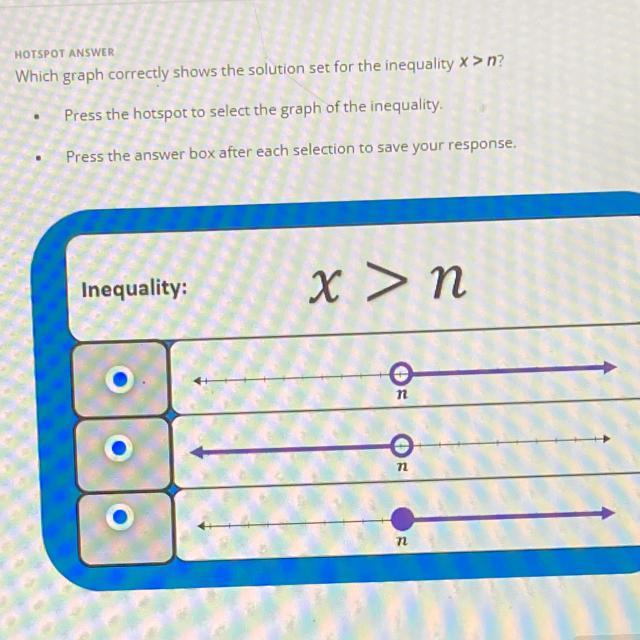
Answers
Answer:
first graph
Step-by-step explanation:
x > n
the graph will have an open circle at the value n , indicating that x cannot equal n ( note solid circle if x ≥ n )
the arrow from n will point in the right direction, indicating values of x greater than n.
the graph representing x > n is the first graph
(4x-10) x (3x²)
Find the area of the rectangle
Answers
If the length of the rectangle be (3x+2) units and width (4x+10)units then the area of the rectangle be \($x=-\frac{2}{3}, x=-\frac{5}{2}$$\).
How to find the area of rectangle?The region enclosed by an object's shape is referred to as the area. The area of the shape is the area that the figure or any other two-dimensional geometric shape occupies in a plane.
A rectangle's sides determine its area. In essence, the length and breadth of the rectangle multiplied together gives the area of the rectangle.
Let the length of the rectangle be (3x + 2) units and width of the rectangle be (4x + 10)units.
Area of rectangle = length × breadth
= (3x +2) × (4x +10)
simplifying the above equation, we get
= (3x) × (4x +10) + 2(4x +10)
= 12x² + 30x +8x +20
12x² + 38x + 20 = 0
simplifying the above equation, we get
By using quadratic equation, then
\($x_{1,2}=\frac{-38 \pm \sqrt{38^2-4 \cdot 12 \cdot 20}}{2 \cdot 12}$$\)
simplifying the above equation, we get
\($$\begin{gathered}x_{1,2}=\frac{-38 \pm 22}{2 \cdot 12}\end{gathered}$$\)
Separate the solutions, we get
\($$\begin{aligned}& x_1=\frac{-38+22}{2 \cdot 12}, x_2=\frac{-38-22}{2 \cdot 12} \\& x=\frac{-38+22}{2 \cdot 12}:-\frac{2}{3} \\& x=\frac{-38-22}{2 \cdot 12}:-\frac{5}{2}\end{aligned}$$\)
The solutions to the quadratic equation are:
\($x=-\frac{2}{3}, x=-\frac{5}{2}$$\)
The complete question is:
Find the area of rectangle with length (3x+2) units and width (4x+10)units.
To learn more about area refer to:
https://brainly.com/question/2607596
#SPJ1
Mark studies a parallelogram and finds the slope of the diagonals to be5/3and -3/5 what cinjecture can be made
Answers
From Mark studies of a parallelogram and discovering that the slope of the diagonals are 5/3 and -3/5 the conjecture that can be made is
The diagonals are perpendicular to each other
What are perpendicular lines?The two different lines that cross each other at a 90° angle are called perpendicular lines.
If two lines intersect at a 90 degree angle, we say that the two lines are perpendicular.
Perpendicular lines have a feature which relates with the slope of the line as being a negative reciprocal
In the context of the given problem,
diagonal 1 has slope 5/3, the negative reciprocal is -3/5.
Since the two diagonals posses this relationship they are said to be parallel
Learn more on slope of a perpendicular line at:
https://brainly.com/question/28804591
#SPJ1
The function h(x) is a transformation of the square root parent function,
f(t) = t. What function is H(x)?

Answers
Answer:
A. \(h(x)=\sqrt{x-3}\)
Step-by-step explanation:
Step 1: DefinitionThe parent function of \(\sqrt{x}\) is translated to the left when \(h\) is positive in the transformation \(\sqrt{x+h}\).
If \(h\) is negative, the graph translates towards the left with the distance equal to the value of \(h\).
Step 2: ImplementationHere the graph moved 3 units towards the right. This means that \(h\) is negative and has the value of 3.
So, plugging that into the parent function for translation, the function becomes:
\(h(x)=\sqrt{x-3}\)
NO LINKS!! Describe the set of all points P(x, y) in a coordinate plane that satisfy the given condition. Part 2

Answers
Part (d)
If xy > 0, then the two items x and y must have the same sign.
Examples where x,y are both positive
x = 2 and y = 5 leads to xy = 2*5 = 10x = 7 and y = 4 leads to xy = 7*4 = 28Examples where x,y are both negative
x = -1 and y = -9 leads to xy = -1*(-9) = 9x = -12 and y = -3 leads to xy = -12*(-3) = 36This places us in either the first quadrant or third quadrant (Q1 and Q3)
Q1 is where x > 0 and y > 0 (northeast corner)Q3 is where x < 0 and y < 0 (southwest corner)Answer: The set of all points in quadrants I and III (x and y have the same sign)======================================================
Part (e)
If y < 0, then we have points like (2,-5) and (1,-7). The x coordinate doesn't matter as long as the y coordinate is negative.
Visually speaking we are below the x axis. This places the point in Q3, Q4, or on the negative y axis. The point cannot be on the x axis. You can think of this point as being underground or underwater.
Answer: The set of all points below the x axis======================================================
Part (f)
If x = 0, then the point is on the vertical y axis. Recall that y intercepts always occur when x = 0. Two examples would be (0,4) and (0,12).
Answer: The set of all points on the y axis.Answer:
(d) The set of all points in quadrants I and III (x and y have the same sign).
(e) The set of all points below the x-axis.
(f) The set of all points on the y-axis.
Step-by-step explanation:
The Cartesian plane is divided into four quadrants.
Quadrant I is the upper right quadrant and the rest follow in a counterclockwise direction.
Quadrant I: x > 0 and y > 0 → (x, y)Quadrant II: x < 0 and y > 0 → (-x, y)Quadrant III: x < 0 and y < 0 → (-x, -y)Quadrant IV: x > 0 and y < 0 → (x, -y)Part (d)
For xy > 0, x and y should either both be positive or both be negative, i.e. have the same sign.
x and y are both positive in quadrant I.x and y are both negative in quadrant III.Therefore, the description that satisfies the given condition is:
The set of all points in quadrants I and III (x and y have the same sign).Part (e)
For y < 0, y is always negative.
y is negative in quadrant III.y is negative in quadrant IV.Quadrants III and IV are below the x-axis.
Therefore, the description that satisfies the given condition is:
The set of all points below the x-axis.Part (f)
The only place where x = 0 is the y-axis.
Therefore, the description that satisfies the given condition is:
The set of all points on the y-axis.
The question is in the picture.

Answers
Easy way to do this, divide 24 with 3, you will get 8. That means 8 is 1/3 of 24. To get 2/3 you just add 8+8 which equals to 16
(9x+5)+(-2x^2+10x)
(9x+5)+(−2x
2
+10x)
Answers
Answer:
If i´m correct and read the answer correct it should be:
-18x³+80x²+65x+5
Step-by-step explanation:
Hopefully this is correct, I couldn't understand if (-2x 2+10x) was spaced or if it was being multiplied.
Thirteen students entered the business program at Sante Fe College 2 years ago. The following table indicates what each student scored on the high school SAT math exam and their grade-point averages (GPAs) after students were in the Sante Fe program for 2 years.
Student A B C D E F G
SAT Score 421 375 585 693 608 392 418
GPA 2.93 2.87 3.03 3.42 3.66 2.91 2.12
Student H I J K L M
SAT Score 484 725 506 613 706 366
GPA 2.50 3.24 1.97 2.73 3.88 1.58
The least-squares regression equation that shows the best relationship between GPA and the SAT score is:_____.
Answers
Answer:
Kindly check explanation
Step-by-step explanation:
Given the following :
SAT SCORE :
421
375
585
693
608
392
418
484
725
506
613
706
366
GPA:
2.93
2.87
3.03
3.42
3.66
2.91
2.12
2.50
3.24
1.97
2.73
3.88
1.58
Using the online linear regression calculator ; the regression model obtained is :
ŷ = 0.00345X + 1.00301
0.00345 = slope or gradient
1.00301 = intercept ; where the regression line crosses the y axis
X = independent variable or predictor variable ; y = dependent variable or predicted variable
After working satisfactorily for 6 months, Collin will be eligible for a 7% raise. How much will Collin's
gross salary be, after her raise, for each 2-week pay period? His current gross salary is $1,083.34.
Answers
Collin's gross salary, after the 7% raise, for each 2-week pay period, will be approximately $1,159.17.
To calculate Collin's gross salary after the 7% raise for each 2-week pay period, we need to find the raise amount and add it to his current gross salary.
Collin's current gross salary is $1,083.34.
To find the raise amount, we multiply his current gross salary by 7% (or 0.07):
Raise amount = $1,083.34 \(\times\) 0.07
= $75.8338 (rounded to two decimal places)
Now, we add the raise amount to his current gross salary to find the new gross salary:
New gross salary = $1,083.34 + $75.8338 = $1,159.1738 (rounded to two decimal places)
For similar question on gross salary.
https://brainly.com/question/28905653
#SPJ8
Philip is snorkeling along a coral reef. He’s wearing an altimeter, which tracks his elevation. Philip snaps a picture of the reef at an elevation of -10 1/2 feet. Then he spots a nurse shark and swims to it for a closer look. By the time he reaches the shark, his elevation changes by -3 1/2 feet.
What is Philip’s elevation when he reaches the shark?
Answers
-7 feet
kinda guessing but it seems correct
The probability of winning a certain game is 0.5. If at least 70 percent of the games in a series of n games are won, the player wins a prize. If the possible choices for n are
n=10, n=20, and n=100,
which value of n should the player choose in order to maximize the probability of winning a prize?
a. n=10 only
b. n =20 only
c. n = 100 only
d. n =10 or n =20 only; the probabilities are the same.
e. n=10 or n=20 or n=100 ; the probabilities are the same.
Answers
The probability of winning a prize remains the same for,
e. n = 10 or n=20 or n = 100; the probabilities are the same.
What is the binomial theorem on probability?In an experiment with two possible outcomes, the likelihood of exactly x successes on n repeated trials is known as the binomial probability (commonly called a binomial experiment).
From the information we get,
p = 0.5, So, q = 1 - 0.5 = 0.5.
If 70% of 'n' games are won then 30% of n games must be lost.
Let n = 10.
∴ \(P(x = 3) = ^{10}C_3p^7q^3\).
\(P(x = 3) = ^{10}C_3(0.5)^7(0.5)^3\).
P(x = 3) = 120×0.0078×0.125.
P(x = 3) = 0.117 Or 11.7% chance.
Now, Changing the value as all the 'n's are multiple of 10 and we'll have the same probability.
learn more about the binomial theorem on probability here :
https://brainly.com/question/29350029
#SPJ1
3km 5hm multiplied by 15 equals what
Answers
Answer: 525
Step-by-step explanation:
3 km =30 hm
35hm*15=525
please help i really need it i have been working on this for the past 42 minutes

Answers
Solve | 2x | = | x + 3 | by graphing

Answers
Answer:the answer is 3 and -1
Step-by-step explanation:
X=3
And
X=-1
A man bought two pencils and three biros at a cost of 50, Again he bought three pencils and four biros for 70. find the cost of a pencil and a biro
Answers
From the first statement, we can write:
2x + 3y = 50 ...(1)
Similarly, from the second statement, we can write:
3x + 4y = 70 ...(2)
We now have two equations with two unknowns. We can solve for x and y using elimination or substitution method. Let's use the elimination method:
Multiplying equation (1) by 3 and subtracting it from equation (2) multiplied by 2, we get:
(2)(3x + 4y) - (3)(2x + 3y) = (70)(2) - (50)(3)
Simplifying, we get:
2x + 5y = 40 ...(3)
Now we have two equations with two unknowns:
2x + 3y = 50 ...(1)
2x + 5y = 40 ...(3)
Subtracting equation (1) from equation (3), we get:
2y = -10
Therefore, y = -5
Substituting y = -5 in equation (1), we get:
2x + 3(-5) = 50
Simplifying, we get:
2x = 65
Therefore, x = 32.5
Hence, the cost of a pencil is 32.5 cents and the cost of a biro is -5 cents.
However, it is not possible for the cost of a biro to be negative, so there must be an error in the calculations or in the problem statement. Please check the numbers and the problem statement again.
Find the probability that a randomly selected point within the square falls in the red-shaded triangle. 3 3 4 P = [?] 4
Answers
The required probability is 3 √7 / 32.
Given, a square with sides of length 4 units and a red-shaded triangle with sides 3 units, 3 units and 4 units. We need to find the probability that a randomly selected point within the square falls in the red-shaded triangle.To find the probability, we need to divide the area of the red-shaded triangle by the area of the square. So, Area of square = 4 × 4 = 16 square units. Area of triangle = 1/2 × base × height.
Using Pythagorean theorem, the height of the triangle is found as: h = √(4² − 3²) = √7
The area of the triangle is: A = 1/2 × base × height= 1/2 × 3 × √7= 3/2 √7 square units. So, the probability that a randomly selected point within the square falls in the red-shaded triangle is: P = Area of triangle/Area of square= (3/2 √7) / 16= 3 √7 / 32.
for such more questions on probability
https://brainly.com/question/29070527
#SPJ8
Medical records indicate that people with more education tend to live longer; the correlation is 0.48. The slope of the linear model that predicts lifespan from years of education suggests that on average people tend to live 0.8 extra years for each additional year of education they have. The slope of the line that would predict years of education from lifespan is
Answers
Answer:
0.288
Step-by-step explanation:
Given that :
Correlation (R) = 0.48
Slope of linear model which predicts Lifespan from years of education (m) = 0.8
To determine the value of slope of the model which predicts years of eductauoon from lifespan:
The square of the regression Coefficient is multiplied by the inverse of the slope of linear model which predicts Lifespan from years of education
Hence,
(R² * 1/m)
0.48² * 1/0.8
0.2304 * 1.25
= 0.288
32. Jimmy is putting down carpet in a square-shaped room. The floor has an area of
90 square feet. Jimmy knows that the side length of the floor must be √90 feet.
Which statement about the value of √90 feet is true?
A. √90 feet is between 9 feet and 10 feet but is closer to 9 feet.
B. √90 feet is between 9 feet and 10 feet but is closer to 10 feet.
C. √90 feet-45 feet
D. √90 feet = 8100 feet
Answers
Answer:
The correct answer is A.
Step-by-step explanation:
The correct answer is A.
To find the length of one side of the square, we need to take the square root of the area. Therefore, the square root of 90 is approximately 9.49 feet. Since this value falls between 9 feet and 10 feet, but is closer to 9 feet, the statement "√90 feet is between 9 feet and 10 feet but is closer to 9 feet" is true. So, Jimmy should cut the carpet to 9.49 feet to fit the square-shaped room.
Estimate The problem
2,731÷31
Answers
Answer:
your answer should be 90
Step-by-step explanation:
Answer:
90
Step-by-step explanation:
Start by rounding both numbers, 2700 divided by 30
giving you, 90
x = 13, ¿cuál ecuación es verdadera?
3(18 - x) = 67
4(9x) = 23
2(x-3)=7
5(x-9) = 20
Answers
When x = 13, the equation that is true is option D) 5(x - 9) = 20.
To determine which equation is true when x = 13, we can substitute the value of x into each equation and see which equation holds true. Let's go through each option:
A) 3(18 - x) = 67
Substituting x = 13:
3(18 - 13) = 67
3(5) = 67
15 = 67
The equation is not true when x = 13. Therefore, option A is false.
B) 4(9x) = 23
Substituting x = 13:
4(9*13) = 23
4(117) = 23
468 = 23
Again, the equation is not true when x = 13. Therefore, option B is also false.
C) 2(x - 3) = 7
Substituting x = 13:
2(13 - 3) = 7
2(10) = 7
20 = 7
Once again, the equation is not true when x = 13. Therefore, option C is false as well.
D) 5(x - 9) = 20
Substituting x = 13:
5(13 - 9) = 20
5(4) = 20
20 = 20
Finally, the equation is true when x = 13. Therefore, option D is true.
For more such questions on equation visit:
https://brainly.com/question/30451972
#SPJ8
Note: the translated questions is
X = 13, which equation is true?
50 Points
In the figure below ABC~YXZ. Find sinX, tanX, and cosX. Round your answers to the nearest hundredth.

Answers
If ABC~YXZ, then the corresponding angles are equal. Therefore:
- sinX = sin(A), where A is the corresponding angle of X in triangle ABC.
- cosX = cos(A), where A is the corresponding angle of X in triangle ABC.
- tanX = tan(A), where A is the corresponding angle of X in triangle ABC.
To find sin(A), cos(A), and tan(A), you will need to use the ratios of the sides of triangle ABC. The most common way to do this is by using the Pythagorean theorem and the definitions of sine, cosine, and tangent:
- sin(A) = opposite / hypotenuse
- cos(A) = adjacent / hypotenuse
- tan(A) = opposite / adjacent
You will need to identify which side is the hypotenuse, opposite, and adjacent for angle A in triangle ABC. Then, plug in the values into the appropriate formula to find sinX, tanX, and cosX, rounding your answers to the nearest hundredth.
why do you think that it is wise to take a gap year after school
Answers
Answer:
to figure things out
Step-by-step explanation:
Answer:
I think it's wise to take a gap year after school because As you know usually most students study forcefully or not tho forcefully but studying for marks only.BUT after school the other studies are the main one Yes the school is the students place where people make their life starts that's what people say
BUT I WOULD SAY THAT
school tho might be the starting point
BUT
after school studies are the one which is a total decisive one can't study after schools again with force and for marks
so if there is a gap after school and the person understands the thing about study than one can study for oneself
SO I SAY IT IS WISE
1/4 of women have a disability. If there are 56 women in a
group.. how many would you expect to have a disability?
Answers
Answer:
14
Step-by-step explanation:
Because 1/4 of women have a disability, you would expect 1/4 * 56 = 14 women to have a disability out of 56 women.
Answer:
224
Step-by-step explanation:
You divide 56 divided by 1/4 and you will get your answer
find the lcm of 6x^2and15xy^2z
Answers
Step-by-step explanation:
it is very easy
just take common factor a day remaining factor
so at last common factor multiplied by remaining factor
Please fast!!!!!!!!!!!!!!!! Triangle 1 and triangle 2 are similar right triangles formed from a ladder leaning against a building.
Triangle 1 Triangle 2
The distance, along the ground, from the bottom of the ladder to the building is 12 feet. The distance from the bottom of the building to the point where the ladder is touching the building is 18 feet. The distance, along the ground, from the bottom of the ladder to the building is 8 feet. The distance from the bottom of the building to the point where the ladder is touching the building is unknown.
Determine the distance from the bottom of the building to the point where the ladder is touching the building for triangle 2.
27 feet
18 feet
12 feet
5 feet
Answers
The distance from the bottom of the building to the point where the ladder is touching the building for triangle 2, obtained using trigonometric ratio of tangent is 12 feet. The correct option is therefore;
12 feet
What are the trigonometric ratios?The trigonometric ratios are the value relationship between an interior angle of a right triangle and two of the sides of the triangle.
The right triangles are similar, therefore, the tangent of the angle the ladder makes with the ground are the same, which indicates;
tan(θ) = (Length of the side facing the angle θ) ÷ (Length of the side adjacent to the angle θ)
The side facing the angle is the distance from the bottom to the point where the ladder touches the building.
The adjacent to the angle is the horizontal distance from the bottom to the ladder to the building.
Therefore; tan(θ) = 18/12 = x/8
Where x = The distance from the bottom of the building to the point the ladder touches the building for triangle 2
18/12 = x/8
x = 18/12 × 8 = 12
The distance, x = 12 feet
Learn more on the tangent of an angle here: https://brainly.com/question/13952108
#SPJ1
Answer:
12?
Step-by-step explanation:
I'm not too sure! I am in the middle of taking the test right now.
Frank buys p ponds or oranges for $2.29 per pound and the same number of pounds of apples for $1.69 per pound. What does the expression 2.99p+1.69p repres
Answers
Answer:
Cost price of buying p pounds of oranges and apples.
Step-by-step explanation:
Cost price is the total amount incurred in procuring a particular commodity. It is usually calculated by taking the cost of each product and the number of products bought.
In this problem;
Cost price of Oranges = Number of pounds of oranges x cost per pound of orange
Cost price of Oranges = p x $2.29 = $2.29p
Cost price of Apples = Number of pounds of Apples x cost per pound of apples
Cost price of Apples = p x $1.69 = $1.69p
The total cost of purchasing orange + apples = 2.29p + 1.69p
So, 2.29p + 1.69p represents the total cost of purchasing apples and oranges.
how do i work this out.
write 600 as the product of prime factors. Give your answer in index form
Answers
If a polynomial function f(x) has roots -7, 1 and 5i, what must also be a root of f(x)?
a) -5
b) -5i
c) 5+i
Answers
Answer:
-5i
Step-by-step explanation:
Please help me w this

Answers
The solution of the given algebraic expression is: ⁷/₁₂ + ⁴/₆q
How to solve Algebraic Expressions?We are given the algebraic expression as:
¹¹/₁₂ - ¹/₆q + ⁵/₆q - ¹/₃
Combining Like terms gives us:
(¹¹/₁₂ - ¹/₃) + (⁵/₆q - ¹/₆q)
Solving both brackets individually gives us:
((11 - 4)/12) + ⁴/₆q
= ⁷/₁₂ + ⁴/₆q
Thus, we conclude that is the solution of the given algebraic expression problem
Read more about Algebraic Expressions at: https://brainly.com/question/4344214
#SPJ1
just pls helpp
no links

Answers
Answer:
1120
Step-by-step explanation:
Answer:
46 in x 28 in = 1288 in^2
Step-by-step explanation:
First you would have to find the height and the width. Then you would have to times the height time width with the height is 28 in and the width is 48 in then you just have to multiply the witch you then turn out with 1288 and you just put the in^2 at the end so your answer is 1288 in^2.