Identify the set of possible values,
a, such that
x-a is a factor of x^5+3x-5
a) (1, 3, 5)
b) (1,5)
c) (1/5, 1, 5)
d) (1, 5)
Answers
The set of possible values for "a" such that (x-a) is a factor of x^5+3x-5 is (1, 5).
To find the set of possible values for "a," we need to determine the values that make (x-a) a factor of the given polynomial, x^5+3x-5. A polynomial (x-a) is a factor of another polynomial if and only if the polynomial evaluates to zero when the factor is substituted for "x."
Using synthetic division or long division, we can divide the polynomial x^5+3x-5 by (x-a) to see if the remainder is zero. If the remainder is zero, then (x-a) is a factor of the polynomial.
By performing the division, we find that for (x-a) to be a factor, the remainder should be zero. However, it is not possible to determine the exact values of "a" that satisfy this condition without performing the division.
Therefore, based on the given answer choices, the set of possible values for "a" is (1, 5). It implies that substituting either 1 or 5 for "a" will make (x-a) a factor of the polynomial x^5+3x-5.
Note: It's important to mention that without additional information or calculations, we cannot determine the complete set of possible values for "a." The given answer choices restrict the options to (1, 3, 5) or (1, 5), but there may be other values of "a" that satisfy the condition as well.
Learn more about factor here : brainly.com/question/14549998
#SPJ11
Related Questions
48 X 25 = 24 x is what
Answers
Answer:
x=50
Step-by-step explanation:
1. multiply the numbers
48x25=24x
1200=24x
2. Divide both sides by the same factor
1200/24 = 24/24x
simplify the expression
x=50
A 13 km stretch of road needs repairs. Workers can repair 3 1/2km of road per week.
How many weeks will it take to repair this stretch of road?
Answers
The workers would need 3.71 weeks to repair the road.
A generalization of arithmetic in which letters representing numbers are combined using arithmetic rules
Given that the total length of the road is 13km. Workers can repair 3.50 roads per week.
To determine the number of weeks required to repair the road, divide the total by per week. The equation would be:
13 ÷ 3.5
= (13 x 10)/35
= 130/ 35
= 3.71
Therefore the workers would need 3.71 weeks to repair the road.
To learn more about algebra visit
https://brainly.com/question/21443100
#SPJ1
Sarah has four friends. Lauren is 1.54m tall, Sophie is 1.50m tall, Kristy is 1.52m tall and Natalie is 1.49m tall. If they all stood on top of eachother how high would theybe?
Answers
Answer:
It would be 6.05m tall.
Several friends (Calvin, Dean, Kelli, and Lee) went to Cal's Late Night Diner for a bite to eat. Match each person to their drink (Iced tea, Lemonade, Root Beer, and Water) and determine how much each paid ($4.99, $5.99, $6.99, and $7.99) for their meal.
Clues:
1. The Diner who paid $4.99 was either Calvin or the one who got the Root Beer.
2. Kelli paid $6.99
3. The one who got the water paid 1 dollar less than Dean.
4. Calvin paid more than Lee.
5. The one who got the Root beer paid 1 dollar less than the one who got the Iced Tea.
Answers
Based on the given clues, we can determine the person, drink, and price paid for each individual:
Calvin: Root Beer, $4.99
Dean: Lemonade, $7.99
Kelli: Water, $6.99
Lee: Iced Tea, $5.99
How to determine how much each friends paidFrom clue 1, we know that either Calvin or the person who got the Root Beer paid $4.99. Since Calvin paid more than Lee according to clue 4, Calvin cannot be the one who got the Root Beer. Therefore, Calvin paid $4.99.
From clue 2, Kelli paid $6.99.
From clue 3, the person who got the water paid $1 less than Dean. Since Dean paid the highest price, the person who got the water paid $1 less, which means Lee paid $5.99.
From clue 5, the person who got the Root Beer paid $1 less than the person who got the Iced Tea. Since Calvin got the Root Beer, Lee must have gotten the Iced Tea.
Therefore, the final assignments are:
Calvin: Root Beer, $4.99
Dean: Lemonade, $7.99
Kelli: Water, $6.99
Lee: Iced Tea, $5.99
Learn more about word problems at https://brainly.com/question/21405634
#SPJ1
Solving the System of Equations
Examine the system of equations.
4.2x + 8y = 41.8
–4.2x + y = 19.4
Use the linear combination method to solve the system of equations. What is the value of x?
–3
–1
1.7
6.8
Answers
Answer:
x= -3
Step-by-step explanation:
Solve the following system:
{8 y + 4.2 x = 41.8
y - 4.2 x = 19.4
In the second equation, look to solve for y:
{8 y + 4.2 x = 41.8
y - 4.2 x = 19.4
y - 4.2 x = y - (21 x)/5 and 19.4 = 97/5:
y - (21 x)/5 = 97/5
Add (21 x)/5 to both sides:
{8 y + 4.2 x = 41.8
y = 1/5 (21 x + 97)
Substitute y = 1/5 (21 x + 97) into the first equation:
{4.2 x + 8/5 (21 x + 97) = 41.8
y = 1/5 (21 x + 97)
4.2 x + (8 (21 x + 97))/5 = ((168 x)/5 + 776/5) + 4.2 x = 37.8 x + 776/5:
{(37.8 x + 776/5) = 41.8
y = 1/5 (21 x + 97)
In the first equation, look to solve for x:
{37.8 x + 776/5 = 41.8
y = 1/5 (21 x + 97)
37.8 x + 776/5 = (189 x)/5 + 776/5 and 41.8 = 209/5:
(189 x)/5 + 776/5 = 209/5
Subtract 776/5 from both sides:
{(189 x)/5 = -567/5
y = 1/5 (21 x + 97)
Multiply both sides by 5/189:
{x = -3
y = 1/5 (21 x + 97)
Substitute x = -3 into the second equation:
Answer: {x = -3, y = 34/5
Answer:
A) -3
Step-by-step explanation:
Plane A is descending toward the local airport, and plane B is ascending from the same airport. Plane A is descending at a rate of 2,500 feet per minute. Plane B is ascending at a rate of 4,000 feet per minute. If plane A is currently at an altitude of 14,000 feet and plane B is at an altitude of 1,000 feet, how long will it take them to be at the same altitude? The equation representing plane A’s descent is y = -2,500x + 14,000. The equation representing plane B’s ascent is y = 4,000x + 1,000. In both equations, y represents altitude and x represents time in minutes.
Answers
Answer: 2 minutes
Step-by-step explanation:
Given the following :
Plane A's descent :
y = -2,500x + 14,000
Plane B's Ascent :
y = 4,000x + 1,000
where y = altitude x = minute
Time to be at the same altitude :
Being at the same altitude means ;
Plane A's descent = Plane B's Ascent
-2,500x + 14,000 = 4,000x + 1,000
-2500x - 4000x = 1000 - 14000
-6500x = - 13000
x = 13000 / 6500
x = 2
x = 2minutes.
Do you know the adjustments for the graph to show the intersecting lines.
A researcher wants to know if a new type of exercise improves people’s health. Would this be a one-tailed or a two-tailed test and why?
a) One-tailed because the study is only interested in whether exercise increases health. b) One-tailed because the study only looks at the effects of exercise and does not take other factors into account. c) Two-tailed because they will have to study healthy and unhealthy people. d) Two-tailed because there is no predicted direction of the difference.
Answers
Two-tailed because there is no predicted direction of the difference. The correct answer is D.
In hypothesis testing, a one-tailed test is used when the researcher has a specific prediction about the direction of the effect. They expect the results to be either greater than or less than a certain value. However, in this scenario, the researcher simply wants to investigate whether the new type of exercise improves people's health without any specific directional prediction.
A two-tailed test is appropriate when the researcher wants to determine if there is a significant difference between the groups being compared, but without specifying the direction of the difference. In this case, the researcher wants to examine if the new exercise has any effect on health, whether it improves or worsens it. Therefore, a two-tailed test is suitable as it allows for the possibility of observing a significant difference in either direction.
Therefore, considering these factors, the researcher should conduct a two-tailed test to assess the potential impact of the new exercise on people's health. The correct answer is D.
To learn more about Two-tailed from the given link
https://brainly.com/question/30818311
#SPJ4
answer for brainilest and 11 points

Answers
Answer:
-16/3
Step-by-step explanation:
I am not sure if you are aware of this but I am not sure if you are aware of the fact
Isolate the variable by dividing each side by factors that don't contain the variable.
the physical plant at the main campus of a large state university receives daily requests to replace fluorescent light bulbs. the distribution of the number of daily requests is bell-shaped and has a mean of 52 and a standard deviation of 7. using the empirical rule rule, what is the approximate percentage of lightbulb replacement requests numbering between 38 and 52? do not enter the percent symbol.
Answers
47.5% between 38 and 52 requests for new lightbulbs have been made.
Given,
The physical plant at the main campus of a large state university receives daily requests to replace fluorescent light bulbs.
The mean of the distribution, μ = 52
Standard deviation, σ = 7
We have to find the approximate percentage of lightbulb replacement requests numbering between 38 and 52 using empirical rule;
Here,
z score corresponding to 38 and 52
z score = (x - μ) / σ = (38 - 52) / 7 = -2
Now,
z score corresponding to 52
z score = 52 -52 / 7 = 0/7 = 0
We are aware that, in accordance with the empirical rule, 68% of the data are within one standard deviation of the mean and 95% are within two.
By comparing the z-scores of data point 38 and 52, we can observe that data point 38 is at the mean. 38 is therefore -2 standard deviations above the mean. That is -2σ to 2σ
The center of the normal distribution curve is known to be the mean. Therefore, we will divide 95% by 2 to obtain the percentage of data points 2 SD above the mean.
95/2 = 47.5%
As a result, 47.5% between 38 and 52 requests for new lightbulbs have been made.
Learn more about standard deviation here;
https://brainly.com/question/16623552
#SPJ4
A hot air balloon is flying at a constant speed of 20 mi/h at a bearing of N 36° E. There is a 10mi/h cross wind blowing due east. What is the balloon's actual speed and direction? Round angles to the nearest degree and other values to the nearest tenth.
Answers:
20.9 mi / h; N 56° E
27.1 mi / h; N 53° E
27.1 mi / h; N 37° E
20.9 mi / h; N 34° E
Answers
Answer:
27.1 mi / h; N 53° E
Step-by-step explanation:
Begin by finding the component form of the two vectors.
The balloon's vector has a magnitude of 20 mi/h and makes an angle of 54° with the x-axis.
The figure shows a vector of balloon speed on a Cartesian plane. The initial point of the vector is the origin. The vector of balloon speed has a length of 20 units. The angle between the vector and the positive direction of the x axis measures 54 degrees.
The balloon's vector components can be determined from the length of the hypotenuse and the angle made with the x-axis.
cos54°=x20
Multiply both sides by 20.
20(cos54°)=x
Calculate and round to the nearest tenth.
11.7≈x
sin54°=y20
Multiply both sides by 20
20(sin54°)=y
Calculate and round to the nearest tenth.
16.2≈y
The balloon's vector is <11.7,16.2>.
Since the wind blows 10 mi/h in the direction of the positive x-axis, it has a horizontal component of 10, and a vertical component of 0.
The figure shows a vector of wind speed on a Cartesian plane. The initial point of the vector is the origin. The vector of wind speed is directed along the positive x axis and has a length of 10 units.
The wind's vector is <10,0>.
To combine the vectors, add the components of the balloon's vector and the wind's vector .
<11.7,16.2>+<10,0>=<21.7,16.2>
The resultant vector in component form is <21.7,16.2>.
The magnitude of the resultant vector is the balloon's actual speed. To find the magnitude of the resultant vector, use the Distance Formula.
∣∣<21.7,16.2>∣∣=(21.7)2+(16.2)2‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√
Simplify.
∣∣<21.7,16.2>∣∣=470.89+262.44‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾√
Simplify again.
∣∣<21.7,16.2>∣∣=733.33‾‾‾‾‾‾‾√
Simplify the square root and round to the nearest tenth.
∣∣<21.7,16.2>∣∣≈27.1 mi/h
The figure shows a vector of balloon speed, a vector of wind speed and a resultant vector on a Cartesian plane. The initial point of the vector of balloon speed is the origin. The initial point of the vector of wind speed is the terminal point of the vector of balloon speed. The initial point of the resultant vector is the origin. The terminal point of the resultant vector is the terminal point of the vector of wind speed. The angle between the resultant vector and the positive direction of x axis is labeled as A.
The angle A is formed by the resultant vector and the x-axis and gives the balloon's actual direction. The tangent of the angle formed with the x-axis is the y component over the x component.
tanA=16.221.7
Solve for m∠A
m∠A=tan−1(16.221.7)
Round to the nearest degree.
m∠A≈37°
This is equivalent to the direction N 53°E, the angle formed by the resultant vector and the y-axis.
Therefore, the balloon's actual speed is 27.1 mi/h, and actual direction is N 53°E.
How do you know if a midpoint Riemann sum is an overestimate or underestimate?
Answers
When the graph is decreasing, the rectangles give an underestimate and when the graph is increasing, they give an overestimate. These trends are accentuated to a greater extent by areas of the graph that are steeper.
We only need to add up the areas of all the rectangles to determine the area beneath the graph of f. It is known as a Riemann sum. The area underneath the graph of f is only roughly represented by the Riemann sum. The subinterval width x=(ba)/n decreases as the number of subintervals n increases, improving the approximation. Increased sections result in an underestimation while decreasing sections result in an overestimation. We now arrive at the middle rule. The height of the rectangle is equal to the height of its right edges for a right Riemann sum and its left edges for a left Riemann sum. The rectangle height is the height of the top edge's midpoint according to the midpoint rule, a third form of the Riemann sum.
Learn more about Riemann Sum here: brainly.com/question/30404402
#SPJ4
In the figure below, the segments FG and FH are tangent to the circle centered at O. Given that OG=8 and FH=8.4, find OF.OF=

Answers
We can conclude that they form a right triangle
So GF = FH
OF^2 = GF^2 + OG^2
OF^2 = 8.4^2 + 8^2
OF^2 = 70.56 + 64
OF^2 = 134.56
OF = 11.6
4. Marcella has 4 fewer male cousins than female cousins. Let f represent the number of female cousins. Write an expression for the number of boy cousins.
Answers
The expression for the number of boy cousins will be f – 4.
What is Algebra?The analysis of mathematical representations is algebra, and the handling of those symbols is logic.
Marcella has 4 fewer male cousins than female cousins.
Let f represent the number of female cousins.
Then the expression for the number of boy cousins will be
⇒ f – 4
More about the Algebra link is given below.
https://brainly.com/question/953809
#SPJ2
HELP WILL GIVE MANY POINTS!!! Need it LIKE NOW
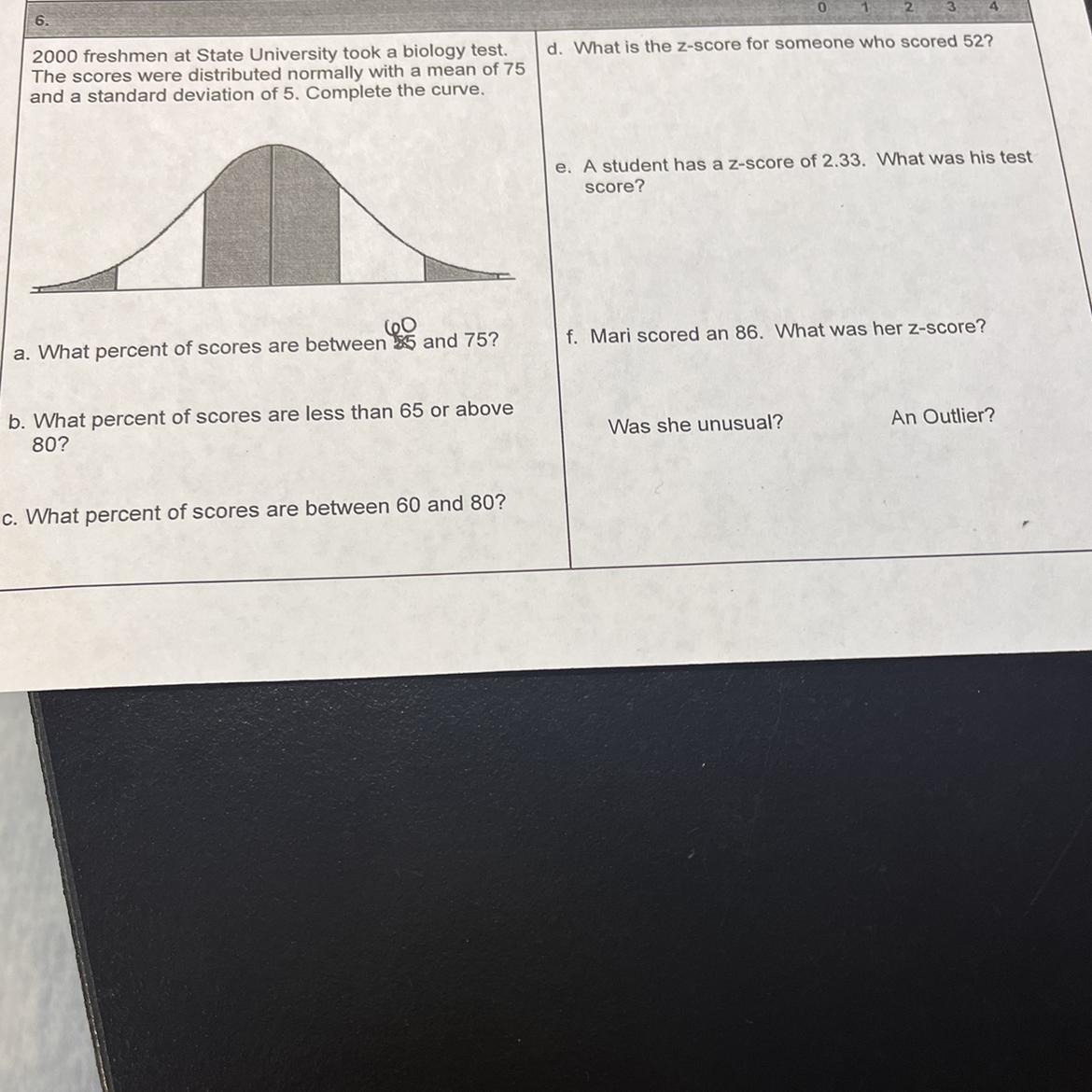
Answers
From the distribution/ probability table,
A The percentage scores are between 60 and 75. is roughly 49.8%
B. The percent of scores that are less than 65 or above 80 is 18.5%
C. The percent of scores between 60 and 80 is 83.85%
D. The Z score for someone who score 52 is -4.6
E. A student with a z-score of 2.33 has 86.65 test score
F. Mari's Z score is 2.2
How do we calculate for figures looking at the distribution table?The easiest way is to map out the spread of the distribution table.
60 65 70 75 80 85 90
Lets share the percentage evenly in the distribution table using the 68, 95 and 99.7 rule.
68% 95% 99.7% 100%
70 -75 = 34% 65-70 = 13.5% 60-65 = 2.35% below 60= 0.15%
75 - 80 = 34% 80 - 85 = 13.5% 85-90 = 2.35% Above 90 = 0.15%
A. For percentage between 60 - 75 we have
60-65 = 2.35%
65-70 = 13.5%
70 -75 = 34%
2.35 + 34% + 13.5% = 49.85%
B. For percentage less than 65 or above 80 we have
below 60= 0.15%
60-65 = 2.35%
85-90 = 2.35%
80 - 85 = 13.5%
Above 90 = 0.15%
0.15 + 0.15 + 2.35+ 2.35 + 13.5 = 18.5%
C. The percent of scores between 60 and 80
60-65 = 2.35%
65-70 = 13.5%
70 -75 = 34%
75 - 80 = 34%
2.35 + 13.5 + 34 + 34 = 83.85%
D. Z score = Z = (X - μ) / σ
Z is the Z-score
X is the value of the element
μ is the population mean
σ is the standard deviation
Z = (52 - 75) / 5 = -23 / 5 = -4.6
E. A student has a z-score of 2.33. What was his test score? We rearrange the formula
X = μ + Zσ = 75 + 2.335 = 86.65
F. Mari scored an 86. What was her z-score?
Z = (86 - 75) / 5 = 11 / 5 = 2.2
Find more exercises on distribution table;
https://brainly.com/question/28821285
#SPJ1
For any positive integer n, let An denote the surface area of the unit ball in Rn, and let Vn denote the volume of the unit ball in Rn. Let i be the positive integer such that Ai>Ak for all k k not equal to i. Similarly let j be the positive integer such that Vj>Vk for all k not equal to j. Find j−i.
Answers
To find the value of j - i, we need to determine the relationship between the surface areas (An) and volumes (Vn) of the unit ball in Rn for different positive integers n.
For the unit ball in Rn, the formula for surface area (An) and volume (Vn) are given by:
An = (2 * π^(n/2)) / Γ(n/2)
Vn = (π^(n/2)) / Γ((n/2) + 1)
where Γ denotes the gamma function.
To find the value of j - i, we need to identify the positive integers i and j such that Ai > Ak for all k not equal to i, and Vj > Vk for all k not equal to j.
First, let's analyze the relationship between An and Vn. By comparing the formulas, we can see that:
An / Vn = [(2 * π^(n/2)) / Γ(n/2)] / [(π^(n/2)) / Γ((n/2) + 1)]
= 2 / [n * (n-1)]
From this equation, we can deduce that An / Vn > 1 if and only if 2 > n * (n-1).
To find the positive integer i, we need to identify the highest positive integer n for which 2 > n * (n-1) holds true. We can observe that this condition is satisfied for n = 2. Therefore, i = 2.
Now, let's find the positive integer j. We need to identify the lowest positive integer n for which 2 > n * (n-1) does not hold true. We can observe that this condition is no longer satisfied for n = 3. Therefore, j = 3.
Finally, we can calculate j - i as follows:
j - i = 3 - 2 = 1
Therefore, j - i equals 1.
To know more about integer visit-
brainly.com/question/32066988
#SPJ11
A 3-column table with 4 rows. Column 1 is labeled Inequality with entries 8 greater-than 2, negative 10 less-than negative 5, 16 greater-than negative 40, negative 8 less-than 4. Column 2 is labeled Multiply each side by: with entries negative 2, 5, 8, negative 4. Column 3 is labeled New Inequality with entries A, B, C, D.
The table gives an inequality and a number to divide both sides of the inequality by. Identify the new, true inequality.
A:
B:
C:
D:
The inequality symbol is only reversed when dividing by a
number.
Answers
Answer:
A:
✔ –4 < –1
B:
✔ –2 < –1
C:
✔ 2 > –5
D:
✔ 2 > –1
The inequality symbol is only reversed when dividing by a
✔ negative
number.
Answer:
1. B
2. B
3. A
4. A
5. negative
Step-by-step explanation:

is a fraction a term? If it's not a term, why is it that we can apply the distributive property to it? the distributive property only works for either terms, or addition and subtraction. a fraction is technically division, so why does it work? Please help!!!!!
Answers
No, a fraction is not a term. The distributive property can be applied to fractions because it is a general mathematical principle.
A fraction is not considered a term in the traditional sense. It is a mathematical expression that represents division. However, the distributive property can still be applied to fractions because the property itself is a fundamental rule of arithmetic that extends beyond specific types of expressions.
The distributive property states that for any real numbers a, b, and c:
a × (b + c) = (a × b) + (a × c).
When working with fractions, we can apply the distributive property as follows:
Let's consider the expression: a × (b/c).
We can rewrite this as: (a × b)/c.
Now, let's distribute the 'a' to 'b' and 'c':
(a × b)/c = (a/c) × b.
In this step, we applied the distributive property to the fraction (a/c) by treating it as a whole.
Although fractions represent division, we can still use the distributive property because it is a general mathematical principle that allows for manipulating expressions involving addition, subtraction, multiplication, and division.
For more such question on fraction
https://brainly.com/question/17220365
#SPJ8
What is the volume of the rectangular prism?

Answers
Answer: 72cm³
Step-by-step explanation:
lengh x width x base with means 6 x 4 x 3
I NEED HELP ASAP!
A pair of similar figures is given below. (Note: the figures are not drawn to scale.)
The sides CD and EF are corresponding sides.
Use the information below to find CD in Figure 1 and the perimeter of Figure 2.

Answers
Answer:
CD is equal to 3.2 m
Perimeter is equal to 37.5 m
what will be the rationalising factor of this thing

Answers
Answer:
dude... I have fallen in love with your profile picture
Iron has a density of 7.9 g/cm³. Gold has a density of 19.3 g/cm³.
I have a piece of metal that has a volume of 200 cm³ and a mass of 3.86 kg. Is it gold or iron?
Answers
3.86kg=3860g
d= 3860/200
= 19.3g/cm^3
therefore it is gold.
unfortunately, the virologist has forgotten which two of the three quantities (infected, susceptible, orimmune people) the functions a and b were modeling. using all the differential equations analysisabilities at your disposal, help the virologist conclusively decide what quantities a and b model.be sure to justify your answer (in particular, rule out the alternatives).
Answers
Once you have followed these steps, you should be able to help the virologist conclusively decide what quantities a and b model by analyzing the given differential equations.
It seems that the specific functions a and b, as well as the differential equations, are not provided in your question. However, I can guide you on how to approach this problem using the given terms and general concepts.
A virologist studies the dynamics of infectious disease using mathematical models. The three quantities of interest are infected people (I), susceptible people (S), and immune people (R). Functions a and b will represent two of these three quantities. To determine which quantities a and b model, we can analyze the given differential equations and follow these steps:
Step 1: Identify the variables and their relationships
Look for the variables (S, I, and R) in the differential equations and analyze how they are related to each other. Determine if there are any rate constants or parameters that link the variables.
Step 2: Analyze the equations' behavior
Study the differential equations' behavior over time, considering different initial conditions. Observe if the equations exhibit any trends, such as an increase or decrease in the quantities.
Step 3: Compare the equations with known epidemic models
Compare the given differential equations with known epidemic models, such as the SIR model or the SEIR model. These models have well-defined equations that describe the rates of change for susceptible, infected, and immune individuals.
Step 4: Rule out alternatives
Based on your analysis, eliminate the alternatives that don't match the behavior exhibited by the differential equations. Ensure that your conclusion is supported by a logical argument.
Once you have followed these steps, you should be able to help the virologist conclusively decide what quantities a and b model by analyzing the given differential equations.
Visit here to learn more about differential equations:
brainly.com/question/14620493
#SPJ11
(3x^-3)^2 what is the degree
Answers
The degree is -6
To simplify, you have to combine the degrees, and you multiply the degree values to get the final degree
Help me:-
Distribute to create an equivalent expression with the fewest symbols possible.
4(5+y) =
Answers
Answer:
20 + 4y
Step-by-step explanation:
The 4 multiplies the 5 and the y, i.e., it distributes over the terms of the expression in ( ).
Along a road there is an emergency telephone every 10 km, a water well every 15 km and a gas station every 20 km. How often do a telephone, a well and a gas station coincide?
Answers
Answer:
60 km
Step-by-step explanation:
Given that :
Location of emergency telephone = every 10km
Location of water well = Every 15 km
Location of gas station = every 20 km
To obtain how often an emergency telephone, water well and gas station coincide, we obtain the lowest common multiple of 10, 15 and 20
Multiples of ;
10 : 10, 20, 30, 40, 50, 60, 70
15 : 15, 30, 45, 60, 75, 90, 105
20 : 20, 40, 60, 80, 100
Hence, the lowest common multiple of 10, 15 and 20 is 60, thus, an emergency telephone line, gas station and water well will coincide every 60km
Зх – 7y = -18
4x – 2y = -24
Answers
Answer:
(-6,0)
Step-by-step explanation:
3x - 7y = -18 -7y = -3x - 18
y = 3/7x + 18/7
4x - 2(3/7x + 18/7) = -24
4x - 6/7x - 36/7 = -24
22/7x = -132/7
x = -6
3(-6) - 7y = -18
-18 - 7y = -18
-7y = 0
y = 0
mr. adams divides 183 markers equally among the 24 students in his class. he puts the extra markers in a box. what is the least number of extra markers in a box?
Answers
Mr. Adams divides 183 markers equally among the 24 students in his class. To find the least number of extra markers in the box, divide the total markers (183) by the number of students (24). The result is 7 with a remainder of 15. So, the least number of extra markers in the box is 15.
Mr. Adams divides 183 markers equally among the 24 students in his class, which means each student gets 7 markers. However, since 7 does not divide evenly into 183, there will be some markers left over. To determine the least number of extra markers in a box, we need to find the remainder when 183 is divided by 24.
Using long division, we get:
24 | 183
-----
7 6
-----
This means that there are 6 markers left over that Mr. Adams puts in a box. Therefore, the least number of extra markers in a box is 6.
Mr. Adams divides 183 markers equally among the 24 students in his class. To find the least number of extra markers in the box, divide the total markers (183) by the number of students (24). The result is 7 with a remainder of 15. So, the least number of extra markers in the box is 15.
learn more about divide here :https://brainly.com/question/14758494
#SPJ11
Emery borrowed money from her brother to buy a new phone and is paying off a fixed amount each week. After 2 weeks, she will owe $456, and after 5 weeks, she will owe $228.
a. Write an equation in point-slope form to represent the situation.
b. What was the original amount Emery owed?
608$
c. How much is being paid each week?
76$
I only need the answer to question 1
Answers
Answer:
A. $608 B. $76
Hope this helps
Answer:
\(y=5w+2w=228\)
Step-by-step explanation:

solve for x and y
x + 10 = 2y - 3
Answers
Answer:
y=13
Step-by-step explanation:
Simplifying y + 10 = 2y + -3 Reorder the terms: 10 + y = 2y + -3 Reorder the terms: 10 + y = -3 + 2y Solving 10 + y = -3 + 2y Solving for variable 'y'. Move all terms containing y to the left, all other terms to the right. Add '-2y' to each side of the equation. 10 + y + -2y = -3 + 2y + -2y Combine like terms: y + -2y = -1y 10 + -1y = -3 + 2y + -2y Combine like terms: 2y + -2y = 0 10 + -1y = -3 + 0 10 + -1y = -3 Add '-10' to each side of the equation. 10 + -10 + -1y = -3 + -10 Combine like terms: 10 + -10 = 0 0 + -1y = -3 + -10 -1y = -3 + -10 Combine like terms: -3 + -10 = -13 -1y = -13 Divide each side by '-1'. y = 13 Simplifying y = 13
Find the square roots of these numbers by division method.
a-6090