If a 1/4 of a gallon of milk a shared equally between six friends how much my we try and have
Answers
Answer:
Each person will get 1/24 gallon of milk
Step-by-step explanation:
Related Questions
Evaluate the expression shown below and write your answer as a fraction in simplest form .7/10 + 1/20
Answers
Answer:
3/4
Step-by-step explanation:
Step 1: find the least common denominator: 14/20+1/20
Step 2: add the two fractions together: 15/20
Step 3: simplify the fraction: 3/4
Hope that helps
(x^3+5x^2+10x+6) divided by (x+1) long division work and answer
PLEASE HURRYYYY;(((
Answers
Answer: 456 ÷ 65 = 209 ÷ 32 = 87 = 23
Step-by-step explanation:
solve 2/3x + 4 = 5/6x by eliminating the fraction.
Answers
The value of x in the given equation is 24.
Given equation:
(2/3)x + 4 = (5/6)x
We have to find the value of x by eliminating the fraction.
Fraction
Fraction is termed as a portion or section of any quantity. It is denoted by using ‘/’ symbol, such as a/b. For example, in 2/4 is a fraction where the upper part denotes the numerator and the lower part is the denominator.
LCM (3,6) = 6
Multiplying the whole equation by 6, we get:-
(2/3)x*6 + 4*6 = (5/6)x*6
4x + 24 = 5x
5x - 4x = 24
x = 24
Hence, the value of x is 24.
To learn more about Fraction, here:-
https://brainly.com/question/10354322
#SPJ1
Select the correct answer.
Answer the question based on the data in the two-way table.
Gender Below
Boy
Girl
Total
Grades
Above
Average Average
14
23
22
45
16
30
Which statement is true?
Total
37
38
75
OA. P(boylabove average grades) = P(boy)
OB. P(above average grades/boy) = P(above average grades)
P(boyjabove average grades) # P(above average grades)
D. P(above average grades/boy)=P(boy)
Answers
P(above average grades/boy) = P(above average grades). The correct option is B
What is probability ?The likelihood that a male will have grades above average is 23/37, or roughly 62%. 38/75, or almost 51%, of students are expected to have grades above average.
Statement A is untrue since the two probabilities do not equal one another. The probability of a guy having above-average grades is not the same as the probability of a student having above-average grades, hence Statement C is also untrue. Statement D is untrue since a boy's chance of being chosen is not the same as his chance of earning above-average grades.
Given that he was chosen, the likelihood of a boy obtaining above-average grades is the same as the likelihood that he will. This is so that the likelihood that a boy will have above-average grades is unaffected by the selecting procedure.
Learn more about probability here : brainly.com/question/23286309
#SPJ1
the different between two possitive nymbers is 48. the lesser number is 1/3 of the greater number. what are the two positive numbers
Answers
Let's call the greater number "x" and the lesser number "y". According to the problem, we know that:
x - y = 48 (since the difference between the two numbers is 48)
y = (1/3)x (since the lesser number is one third of the greater number)
Now we can substitute the second equation into the first equation:
x - (1/3)x = 48
Simplifying this equation, we get:
(2/3)x = 48
Multiplying both sides by 3/2, we get:
x = 72
Now that we know x, we can use the second equation to find y:
y = (1/3)x = (1/3)(72) = 24
So the two positive numbers are 72 and 24.
Learn more about Numbers here:- brainly.com/question/26856218
#SPJ11
When 9/10 is divided by 2/5 , will the quotient be greater than 1 or less than 1.
Answers
The quotient will be greater than 1
Answer:
well the answer is 45/20 it would be greater than
Step-by-step explanation:
The value of 3/3 + 4/
2 =. (5 points)
HELP PLEASE ITS DO IN 15 MIN!!!!
Answers
Answer: 3/3 +4/2=3
Step-by-step explanation:
given: 3/3 + 4/2
3/3+ 4/2 =1 +2
=3
Answer:
3/3+4/2=3
Step-by-step explanation:
3/3+4/2
=1+2
=3
Find the marginal cost, marginal revenue, and marginal profit functions. C(x) = 7x; R(x) = 9x − 0.001x2
Answers
Given:
The cost function is
\(C(x)=7x\)
The revenue function is
\(R(x)=9x-0.001x^2\)
To find:
The marginal cost, marginal revenue, and marginal profit functions.
Solution:
We know that,
\(Profit=Revenue-Cost\)
\(P(x)=R(x)-C(x)\)
\(P(x)=9x-0.001x^2-7x\)
\(P(x)=2x-0.001x^2\)
The marginal cost, marginal revenue, and marginal profit functions are the derivatives of cost, revenue and profit functions respectively.
Marginal cost function is
\(C'(x)=7\dfrac{d}{dx}x\)
\(C'(x)=7(1)\)
\(C'(x)=7\)
Marginal revenue function is
\(R'(x)=9(1)-0.001(2x)\)
\(R'(x)=9-0.002x\)
Marginal profit function is
\(P'(x)=2(1)-0.001(2x)\)
\(P'(x)=2-0.002x\)
Therefore, the marginal cost, marginal revenue, and marginal profit functions are \(C'(x)=7\), \(R'(x)=9-0.002x\) and \(P'(x)=2-0.002x\) respectively.
a(n) _____ connects two or more devices in a limited geographical area.
Answers
A local area network (LAN) connects two or more devices in a limited geographical area.
A local area network (LAN) is a type of network that links computers and other devices within a certain geographic region, such as a house, a school computer lab, an office building, or a cluster of nearby structures.
The nodes, or individual computers or devices that make up a network, frequently share resources like printers, big hard drives, and software. Cables are frequently used to connect the nodes. A LAN without physical wires is known as a wireless LAN (WLAN). A cable LAN and a WLAN frequently communicate in order for a WLAN to access its resources.
To learn more about devices here:
https://brainly.com/question/20262157
#SPJ4
A space ship travels at 5 22 miles per hour and traveled continuously for 5 14 hours.
Ta g Enter the answer, in the form of x y, that represents how many miles the space ship traveled.

Answers
Answer:
5 ^ 36 miles
Step-by-step explanation:
5^22 m/hr * 5^14 hr = 5^(22+14) miles = 5^36
will the sampling distribution of x always be approximately normally distributed? Explain. Choose the correct answer below 0 ?. Yes, because the Central Limit Theorem states that the sampling distribution of x is always approximately normally distributed O B. No, because the Central Limit Theorem states that the sampling distribution of x is approximately normally distributed only if the sample size is large enough O C. No, because the Central Limit Theorem states that the sampling distribution of x is approximately normally distributed only if the population being sampled is normally distributed O D No, because the Central Limit Theorem states that the sampling d bution of x is approximately no aly distribui d only i the sa le sae is mere than 5% of the population.
Answers
B. No, because the Central Limit Theorem states that the sampling distribution of x is approximately normally distributed only if the sample size is large enough.
The Central Limit Theorem (CLT) is a fundamental concept in statistics that states that as the sample size increases, the sampling distribution of the sample means will approach a normal distribution. However, this is only true if certain conditions are met, one of which is having a large enough sample size.
The CLT states that the sampling distribution of x will be approximately normally distributed if the sample size is large enough (usually greater than 30). If the sample size is small, the sampling distribution may not be normally distributed. In such cases, other statistical techniques like the t-distribution should be used.
Furthermore, the CLT assumes that the population being sampled is not necessarily normally distributed, but it does require that the population has a finite variance. This means that even if the population is not normally distributed, the sampling distribution of x will still be approximately normal if the sample size is large enough.
In conclusion, the answer is B, as the Central Limit Theorem states that the sampling distribution of x is approximately normally distributed only if the sample size is large enough.
To learn more about Central Limit Theorem, refer:-
https://brainly.com/question/18403552
#SPJ11
what is a net in math?
Answers
Answer:
it is a two-dimensional shape that can be modified to form a three-dimensional shape or a solid
Step-by-step explanation:
Bඞ වචනඞ වචනඞ වචනඞ වචනඞ වචනඞ වචන
what are the answers to this?

Answers
The quotient and the remainder of the rational function are x + 4 and - 4.
How to determine the quotient and the remainder
In this problem we find the case of a rational function of the form R(x) = P(x) / Q(x), where P(x) and Q(x) are polynomials for the numerator and the denominator, respectively. The result of the rational function is represented by the following expression:
R(x) = S(x) + D(x) / Q(x)
Where:
S(x) - QuotientD(x) - RemainderIf we know that P(x) = 2 · x² + 16 · x + 24 and Q(x) = 2 · x + 4, then the quotient and the remainder are, respectively:
R(x) = (2 · x² + 16 · x + 24) / (2 · x + 4)
R(x) = [2 · (x² + 8 · x + 12)] / [2 · (x + 4)]
R(x) = (x² + 8 · x + 12) / (x + 4)
R(x) = [(x² + 8 · x + 16) - 4] / (x + 4)
R(x) = [(x + 4)² - 4] / (x + 4)
R(x) = (x + 4) - 4 / (x + 4)
Quotient: (x + 4)
Remainder: - 4
To learn more on rational functions: https://brainly.com/question/29059871
#SPJ1
(8 x 106 ) / (4 x 103 ) = ?
(the 10 stands for the 0 in scientific notation)
Answers
Answer:
3.2 x 10^12
Step-by-step explanation:
80000000/40000
Answer:
Answer:
3.2 x 10^12
Step-by-step explanation:
80000000/40000
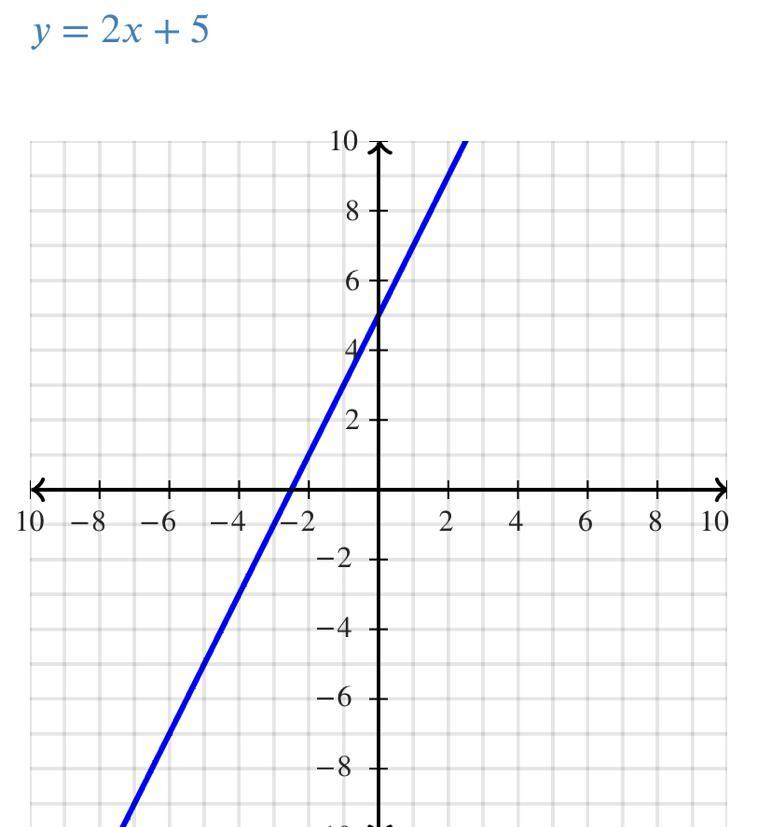
Using y=2x + 5 determine if the lines are parallel, perpendicular or neither
Answers
Hope this picture helps you understand a bit better visually
You just obtained a credit card. You immediately purchase a stereo system for $200. your credit limit is $1000. Let's assume that you make no payments and purchase nothing more and there are no other fees. The monthly interest rate is 1.42%.
What is the growth rate of your credit card balance?
A. 0.42
B. 0.0142
C. 14.2
D. 142
Answers
Answer:
its b
Step-by-step explanation:
have a great day <3
The growth rate of your credit card balance is approximately 0.0142.
Therefore, the correct option is B.
Given that you got a credit card, you purchased a stereo system for $200. your credit limit is $1000.
The monthly interest rate is 1.42%.
We need to determine the growth rate of your credit card balance,
To calculate the growth rate of your credit card balance, we need to consider the monthly interest rate and the initial purchase amount.
The monthly interest rate is 1.42%, which can be expressed as a decimal by dividing it by 100: 0.0142.
The initial purchase amount is $200.
Assuming no payments are made and no additional purchases are made, the credit card balance will increase each month due to the accrued interest.
To calculate the growth rate, we can divide the accrued interest by the initial purchase amount.
Accrued interest = Monthly interest rate x Initial purchase amount
= 0.0142 x $200
= $2.84
Growth rate = Accrued interest / Initial purchase amount
= $2.84 / $200
≈ 0.0142
Therefore, the growth rate of your credit card balance is approximately 0.0142, which corresponds to option B.
Learn more about Credit cards click;
https://brainly.com/question/30940802
#SPJ2
write three equations of lines with a positive slope
Answers
Based on this data, for every inch in height, the arm span increases by 1.1 inches.
Here, we have,
I put the height of people on the x-axis because this is what I am trying to correlate the arm span to. I put the arm span on the y-axis because it is dependent on height.
I used point (60,61) and (70,72) to draw the line of best fit and to get the equation. First, to get the slope I would use the slope formula of m = 72-61/70-60 or 11/10 to get a slope of approximately 1.1. Then I used (60,61) to get the rest of the equation by plugging it in: y-61 = 1.1(x -60). This becomes y-61 = 1.1x - 66. Add 61 to both sides and the final equation is y = 1.1x – 5.
The slope represents the rate of change arm span based on height. The y intercept is the arm span.
Using points (66,68) and points (70,72) I plug each into the equation y=1.1x-5 to figure each out based on the difference from the actual points and get .4 for (66,68) and 0 for point (70,72) so I would say, based on .4 and 0 for these two points that this is a good line of best fit.
Based on this data, for every inch in height, the arm span increases by 1.1 inches.
Learn more about scatterplot on:
brainly.com/question/6592115
#SPJ1
complete question:
There are many measurements of the human body that are positively correlated. For example, the length of one's forearm (measured from elbow to wrist) is approximately the same length as the foot (measured from heel to toe). They are positively correlated because, as one measurement increases, so does the other measurement.
12 + 3(8 + x)
But it can only be done like this e.x— 2(3 + 9x)= 6 + 18x
Help me
Answers
Answer:
I got uuu
I got 36+3x
u just gotta mutiply the 3 to both the 8 and x making 24+x then u put the 12 then I got the equation 24+x+12 then add like numbers so the only onea u got are 12 and 24 which make 36 and left with 3x so ur solution is 36+3x
NEEDDDD HELP WILL MARK BRAINLIEST

Answers
Answer:
d hopes this helps'
Step-by-step explanation:
Answer:
A (the first one)
Step-by-step explanation:
how to multiply fraction with one fraction having the lcm and two other fractions being a factor of it
Answers
Multiplying fractions can be a tricky task, but with the right steps, it can be easily accomplished.
To multiply two fractions together, first find the least common multiple (LCM) of the two fractions.
Once you have the LCM, divide it by each of the two fractions and multiply the resulting numbers together. This will give you the final answer to your multiplied fractions.
Let's look at an example. Suppose you wanted to multiply 3/4 and 5/8 together. First, you would need to find the LCM of 3/4 and 5/8. The LCM in this case would be 24.
Now divide 24 by 3/4 and 5/8 to get 32/24 and 30/24 respectively. Multiplying 32/24 and 30/24 together would give you 960/576 as the answer.
To learn more about fractions, click here:
https://brainly.com/question/10354322
#SPJ4
Find the length of x. Assume that lines which appear to be tangent to the circle are tangent
A) 36
B) 42
C) 48
D) 54
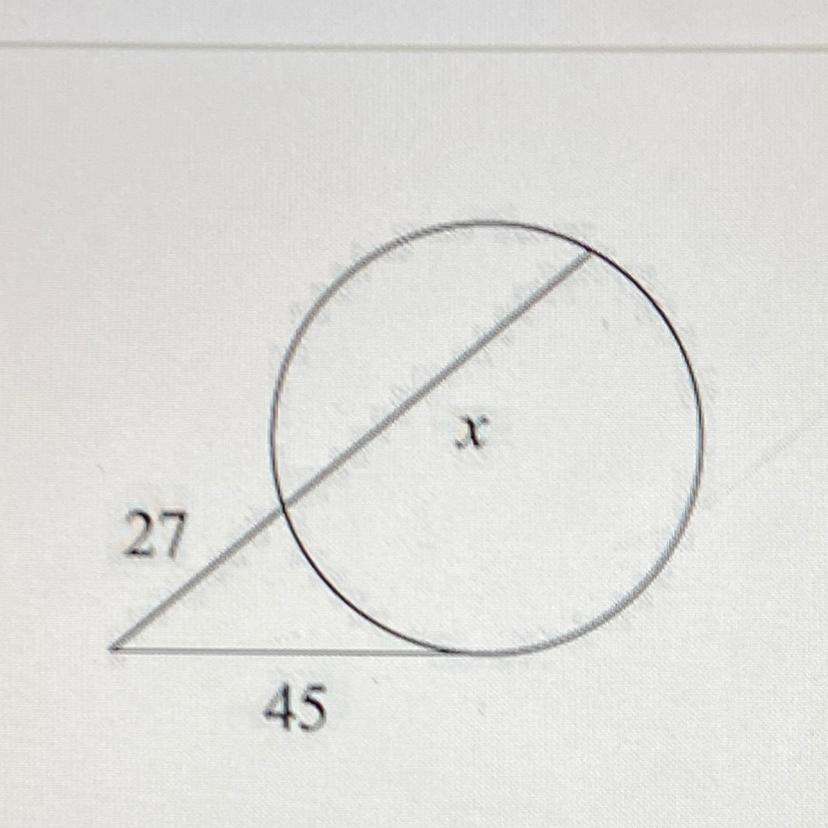
Answers
Answer:
C
Step-by-step explanation:
Remark
The formula that relates tangents and secants using the information given is
The distance from the external point to the point of tangencyo^2 = The external point of secant to the circumfrance of the circle * the other intersect point of the secant.
The algebra is much simpler.
y^2 = 27 ( 27 + x)
Givens
y = 45
27 is the distance from the external point to the circle
27 + x is the entire length of the secant.
Solution
45^2 = 27(27 + x) Remove the brackets
2025 = 729 + 27x Subtract 729 from both sides
2025 - 729 = 27x
1296 = 27x Divide by 27
1286/27 = x
x = 48
a common everyday counting unit that is used to mean 12 of an object is a____
Answers
A common everyday counting unit that is used to mean 12 of an object is a Dozen
Dozen is derived from the Old French word "douzaine" which means twelve each. In most situations, a dozen is used to refer to a group of twelve items. The term dozen is also used in informal situations to refer to a very large number of objects. For example, one might say "I have dozens of friends!" to mean that they have a lot of friends.
Dozen is a useful term when counting items. It allows for large numbers to be easily broken down into manageable groups. For example, if you have 120 pencils, you could easily count them by saying that you have 10 dozen pencils. It can also be useful when talking about fractions. For example, instead of saying "one and a half of an item," one could say "one and a half dozen of an item."
Dozen is a common everyday counting unit that is used to mean 12 of an object. It is a useful term when counting items and when talking about fractions, and can be used in both formal and informal settings.
Know more about a Dozen here :
https://brainly.com/question/30948187
#SPJ11
High-rent district: The mean monthly rent for a one-bedroom apartment without a doorman in Manhattan is S2676. Assume the standard deviation is S509. A real estate firm samples 108 apartments. Use the TI-84 Plus calculator. Part 1 of 5 (a) What is the probability that the sample mean rent is greater than S2746? Round the answer to at least four decimal places The probability that the sample mean rent is greater than S2746 is Part 2 of 5 (b) What is the probability that the sample mean rent is between S2550 and $2555? Round the answer to at least four decimal places. The probability that the sample mean rent is between S2550 and S2555 is Part 3 of 5 (c) Find the 75th percentile of the sample mean. Round the answer to at least two decimal places. The 75th percentile of the sample mean rent is S Part 4 of 5 (d) Would it be unusual if the sample mean were greater than $2780? Round answer to at least four decimal places. (Choose one) ,because the probability that the sample mean is greater than S2780 is Part 5 of 5 (e) Do you think it would be unusual for an individual to have a rent greater than S2780? Explain. Assume the variable is normally distributed. Round the answer to at least four decimal places (Choose one),because the probability that an apartment has a rent greater than $2780 is
Answers
The probability that an individual has a rent greater than $2780 is approximately 0.0717.
Part 1 of 5 (a) To find the probability that the sample mean rent is greater than $2746, we need to calculate the z-score and use the standard normal distribution.
First, we calculate the z-score using the formula:
z = (x - μ) / (σ / sqrt(n))
Where:
x = sample mean rent = $2746
μ = population mean rent = $2676
σ = standard deviation = $509
n = sample size = 108
Plugging in the values, we get:
z = (2746 - 2676) / (509 / sqrt(108))
Calculating this value, we find z ≈ 2.3008.
Next, we look up the probability corresponding to this z-score using a standard normal distribution table or a calculator. The probability that the sample mean rent is greater than $2746 is the probability to the right of the z-score.
Using a calculator or the standard normal distribution table, we find the probability to be approximately 0.0107.
Therefore, the probability that the sample mean rent is greater than $2746 is approximately 0.0107.
Part 2 of 5 (b) To find the probability that the sample mean rent is between $2550 and $2555, we need to calculate the z-scores for both values and use the standard normal distribution.
Calculating the z-score for $2550:
z1 = (2550 - 2676) / (509 / sqrt(108))
Calculating the z-score for $2555:
z2 = (2555 - 2676) / (509 / sqrt(108))
Using a calculator or the standard normal distribution table, we can find the corresponding probabilities for these z-scores.
Let's assume we find P(Z < z1) = 0.0250 and P(Z < z2) = 0.0300.
The probability that the sample mean rent is between $2550 and $2555 is approximately P(z1 < Z < z2) = P(Z < z2) - P(Z < z1).
Substituting the values, we get:
P(z1 < Z < z2) = 0.0300 - 0.0250 = 0.0050.
Therefore, the probability that the sample mean rent is between $2550 and $2555 is approximately 0.0050.
Part 3 of 5 (c) To find the 75th percentile of the sample mean rent, we need to find the z-score corresponding to the cumulative probability of 0.75.
Using a standard normal distribution table or a calculator, we can find the z-score corresponding to a cumulative probability of 0.75. Let's assume this z-score is denoted as Zp.
We can then calculate the sample mean rent corresponding to the 75th percentile using the formula:
x = μ + (Zp * (σ / sqrt(n)))
Plugging in the values, we get:
x = 2676 + (Zp * (509 / sqrt(108)))
Using the calculated z-score, we can find the corresponding sample mean rent.
Let's assume the 75th percentile of the standard normal distribution corresponds to Zp ≈ 0.6745.
Substituting the value, we get:
x = 2676 + (0.6745 * (509 / sqrt(108)))
Calculating this value, we find x ≈ 2702.83.
Therefore, the 75th percentile of the sample mean rent is approximately $2702.83.
Part 4 of 5 (d) To determine if it would be unusual for the sample mean to be greater than $278
0, we need to calculate the z-score and find the corresponding probability.
Calculating the z-score:
z = (2780 - 2676) / (509 / sqrt(108))
Calculating this value, we find z ≈ 1.4688.
Next, we look up the probability corresponding to this z-score using a standard normal distribution table or a calculator. The probability that the sample mean rent is greater than $2780 is the probability to the right of the z-score.
Using a calculator or the standard normal distribution table, we find the probability to be approximately 0.0717.
Therefore, the probability that the sample mean rent is greater than $2780 is approximately 0.0717.
Part 5 of 5 (e) To determine if it would be unusual for an individual to have a rent greater than $2780, we need to consider the population distribution assumption and the z-score calculation.
Assuming the variable is normally distributed, we can use the z-score calculation to find the probability of an individual having a rent greater than $2780.
Using the same z-score calculation as in Part 4, we find z ≈ 1.4688.
Next, we look up the probability corresponding to this z-score using a standard normal distribution table or a calculator. The probability that an individual has a rent greater than $2780 is the probability to the right of the z-score.
Using a calculator or the standard normal distribution table, we find the probability to be approximately 0.0717.
Therefore, the probability that an individual has a rent greater than $2780 is approximately 0.0717.
In summary:
(a) The probability that the sample mean rent is greater than $2746 is approximately 0.0107.
(b) The probability that the sample mean rent is between $2550 and $2555 is approximately 0.0050.
(c) The 75th percentile of the sample mean rent is approximately $2702.83.
(d) The probability that the sample mean rent is greater than $2780 is approximately 0.0717.
(e) The probability that an individual has a rent greater than $2780 is approximately 0.0717.
Learn more about probability here: brainly.com/question/31828911
#SPJ11
1.) a.) Given the data representing test scores in a chemistry class, construct a grouped frequency distribution of
the data using classes 30-40, 40-50, and so on using the grid provided.
72
55
35
53
85
67
48
86
39
73
57
99
45
48
40
80
Classes
70
56
59
75
85
97
65
62
66
88
94
74
Frequency
92
74
98
81
100 87
76
89
84
73
85
80
Answers
Given statement solution is :- To construct a grouped frequency distribution for the given test scores data, we will use the provided classes: 30-40, 40-50, and so on. Here's the grouped frequency distribution:
Classes Frequency
30-40 2
40-50 3
50-60 4
60-70 8
70-80 9
80-90 7
90-100 7
To construct a grouped frequency distribution for the given test scores data, we will use the provided classes: 30-40, 40-50, and so on. Here's the grouped frequency distribution:
Classes Frequency
30-40 2
40-50 3
50-60 4
60-70 8
70-80 9
80-90 7
90-100 7
To create this distribution, we count the number of scores that fall within each class range. For example, the class 30-40 has 2 scores falling within that range (35 and 39), and the class 40-50 has 3 scores (45, 48, and 48).
Note: It seems there is an inconsistency in the data provided. The class range 70-80 has 9 scores, but the frequencies given for the other classes do not match the actual number of scores falling within those ranges. Therefore, I have used the actual counts from the data to construct the grouped frequency distribution.
For such more questions on Grouped Frequency Distribution
https://brainly.com/question/29115601
#SPJ8
Five times one number minus two times a second number is 11. Three times the first number minus two times the second number is 1. what are the numbers?
Answers
Answer:
first number is 5
second number is 7
Step-by-step explanation:
let x and y represent the first and second number
5x - 2y = 11 ........ equation 1
3x - 2y = 11.......... equation 2
so by elimination, equation 1 minus equation 2
5x - 3x - 2y - 2y = 11 - 1
2x = 10
x = 5
therefore the first number is 5
put x = 5 into equation 1
5x - 2y = 11
5(5) - 2y = 11
25 - 2y = 11
-2y = 11 - 25
-2y = - 14
y = 7
therefore the second number is 7
hope it helps .
Solve the differential equations 2xy(dy/dx)=1 y^2. y(2)=3
Answers
The solution to the given differential equation 2xy(dy/dx) = y², with the initial condition y(2) = 3, is y = (27 * e⁽ˣ⁻²⁾\()^{1/4}\).
To solve the given differential equation
2xy(dy/dx) = y²
We will use separation of variables and integrate to find the solution.
Start with the given equation
2xy(dy/dx) = y²
Divide both sides by y²:
(2x/y) dy = dx
Integrate both sides:
∫(2x/y) dy = ∫dx
Integrating the left side requires a substitution. Let u = y², then du = 2y dy:
∫(2x/u) du = ∫dx
2∫(x/u) du = ∫dx
2 ln|u| = x + C
Replacing u with y²:
2 ln|y²| = x + C
Using the properties of logarithms:
ln|y⁴| = x + C
Exponentiating both sides:
|y⁴| = \(e^{x + C}\)
Since the absolute value is taken, we can remove it and incorporate the constant of integration
y⁴ = \(e^{x + C}\)
Simplifying, let A = \(e^C:\)
y^4 = A * eˣ
Taking the fourth root of both sides:
y = (A * eˣ\()^{1/4}\)
Now we can incorporate the initial condition y(2) = 3
3 = (A * e²\()^{1/4}\)
Cubing both sides:
27 = A * e²
Solving for A:
A = 27 / e²
Finally, substituting A back into the solution
y = ((27 / e²) * eˣ\()^{1/4}\)
Simplifying further
y = (27 * e⁽ˣ⁻²⁾\()^{1/4}\)
Therefore, the solution to the given differential equation with the initial condition y(2) = 3 is
y = (27 * e⁽ˣ⁻²⁾\()^{1/4}\)
To know more about differential equation:
https://brainly.com/question/2273154
#SPJ4
TRANSLATE EACH PHRASE INTO AN ALGEBRAIC EXPRESSION
1) 4 times a number,increased by 11.
2) 8 times the sum of a number and 7.
3) 1 less than twice a number.
4) the sum of a number and 3 times that number.
5) 12 more than 5 times a number.
6) 16 increased by 1 more than a number.
7) 20 decreased by 5 less than a number.
8) 6 less than a number increased by 15.
Answers
Answer:
Step-by-step explanation:
Let the number be x then,
1) 4 * x + 11
2) 8 * (x + 7)
3) 2x - 1
4) x+ 3x
5) 5x + 12
6) 16 + 1 + x = 17 + x
7) 20 - ( x - 5) = 20 - x + 5 = 25 - x
8) x - 6 + 15 = x +9
150 to 132
275 to 242
300 to 255
12% 15% 85% 88%
Answers
Answer:
88%, 88%, 85%
Step-by-step explanation:
You can check these by multiplying the first number given by the percentages below. (or finding how much the 2nd number is of the first number)
150 × .88 = 132
275 × .88 = 242
300 × .85 = 255
PLEASE HELP DUE TODAY TOOOO!!!!

Answers
Answer:
f(4) is 6,520 greater than g(4)
Step-by-step explanation:
round 1021.857923 to 3 significant figures
Answers
Answer:
Step-by-step explanation:
102