If f(x) = 4x - 6, what is f(6)?
A. 32
B. 3
o
C. 4
O D. 18
Answers
Answer:
18 is the correct answer
Step-by-step explanation:
to find f(6) you only need to put value 6 in place x and then simple addotion subtraction
f(6)=4(6)-6
f(6)=24-6
f(6)=18
Related Questions
All students wrote the test with an average of 6 points. Exactly 60% of these students passed the test successfully. Those students who successfully passed the test received an average of 8 points. How many points were received on average by those students who did not pass the test successfully?
Answers
Answer:
The average points received by those students who did not pass the test successfully would be 4 points.
Step-by-step explanation:
Step 1: We know that all students wrote the test and received an average of 6 points.
Step 2: We also know that 60% of those students passed the test successfully and received an average of 8 points.
Step 3: This means that the remaining 40% of students did not pass the test successfully.
Step 4: Since the average points for all students was 6 points and the average points for those who passed the test was 8 points, the average points for those who did not pass the test would be 4 points.
Find the equation of a parallel to y=-3x-5 that passes through the point (2,-1)
A) y-1= -1/3 (x-2)
B)y+1=-1/3(x+2)
C)y-1=-3(x+2)
D)y+1=-3(x-2)
Answers
D: y + 1 = -3(x - 2).
Step-by-step explanation:
The slope of the line y = -3x - 5 is -3, since it is in the form y = mx + b, where m is the slope.
A line parallel to this line will have the same slope, -3. Using the point-slope form of a linear equation, we can find the equation of the line:
y - y1 = m(x - x1), where (x1, y1) is the given point.
Plugging in the values, we get:
y - (-1) = -3(x - 2)
Simplifying and rearranging, we get:
y + 1 = -3x + 6
Subtracting 1 from both sides, we get:
y = -3x + 5
Therefore, the answer is option D: y + 1 = -3(x - 2).
Please help me ! I don’t understand :((

Answers
Answer:
(0,a)
Step-by-step explanation:
f(x) = a * b^x
Let x=0
f(0) = a * b^0
= a * 1
=a
(0,a)
using a rulers and a pair of compasses only contruct a triangle pqr such that pq is 7.5cm and qr is 6.1cm if pqr is 45 degree measure pr
Answers
Using a ruler and compasses, draw PQ (7.5cm), locate R using a 6.1cm radius from P, then connect PR. To measure ∠PQR, use a protractor with Q as the center.
To construct triangle PQR with sides PQ = 7.5 cm, QR = 6.1 cm, and ∠PQR = 45 degrees, follow these steps:
1. Draw a line segment PQ of length 7.5 cm using a ruler.
2. Place the compass at point P and draw an arc with a radius of 6.1 cm to intersect PQ. Label this point of intersection as R.
3. Set the compass to a radius of 7.5 cm and draw an arc with center Q.
4. Without changing the compass width, draw another arc with center R to intersect the previous arc. Label this point of intersection as P.
5. Connect points P and Q with a straight line segment to complete triangle PQR.
6. To measure the angle ∠PQR, use a protractor and place it on line segment QR such that the center of the protractor aligns with point Q. Then measure a 45-degree angle starting from the line segment QR and mark the point of intersection on line segment PQ. Label this point as S.
7. Connect points P and S to form the line segment PS.
8. Measure the length of line segment PS using a ruler.
For more such questions on compasses, click on:
https://brainly.com/question/30661844
#SPJ8
Lines s and t represent a system of linear equations.
• Lines passes through the points (0, 2) and
(2, 4)
• Line t passes through the points (-2, -4) and
(2, 0).
IS THIS CORRECT PLS HELP

Answers
All of your answers are correct
Use Euler's method with step size 0.25 to compute the approximate y -values y1, y2, y 3 , and y4 of the solution of the initial-value problem y′=−1+3x+4y, y(0)=−2.
Answers
The y-values of y1, y2, y3, and y4 are -3.5, -4.96875, -7.14551, and -9.72074 by using Euler's method of the equation y′=−1+3x+4y
Step size = 0.25
initial-value = y′=−1+3x+4y
We can use Euler's method with step size h = 0.25 as follows:
y0 = -2
x0 = 0
y1 = \(y0 + hf(x0, y0)\)
y1 = \(-2 + 0.25(-1 + 30 + 4(-2))\)
y1 = -3.5
x1 = x0 + h
x1 = 0 + 0.25
x1 = 0.25
y2 = \(y1 + hf(x1, y1)\)
y2 = \(-3.5 + 0.25(-1 + 30.25 + 4(-3.5))\)
y2 = -4.96875
x2 = x1 + h
x2 = 0.25 + 0.25
x2 = 0.5
y3 = \(y2 + hf(x2, y2)\)
y3 = \(-4.96875 + 0.25(-1 + 30.5 + 4(-4.96875))\)
y3 = -7.14551
x3 = x2 + h
x3 = 0.5 + 0.25
x3 = 0.75
y4 = \(y3 + hf(x3, y3)\)
y4 =\(-7.14551 + 0.25(-1 + 30.75 + 4(-7.14551))\)
y4 = -9.72074
Therefore, we can conclude that the y-values of y1, y2, y3, and y4 are -3.5, -4.96875, -7.14551, and -9.72074.
To learn more about Euler's method
https://brainly.com/question/30860703
#SPJ4
Point M is the midpoint of line segment CD,
shown below.
What are the coordinates of point M?
C (6,10)
M
D (20, 18)
Answers
Answer:
M(13, 14)-------------------------
Each coordinate of the midpoint is the average of endpoints:
x = (6 + 20)/2 = 26/2 = 13y = (10 + 18)/2 = 28/2 = 14Therefore M is (13, 14).
Use the discriminant to determine the number and type of solutions for the equation x^2+49=14x
(A). This equation has 1 real solution and one imaginary solution because the discriminant is negative.
(B). This equation has 2 imaginary solutions because the discriminant is negative.
(C). This equation has 2 real solutions because the discriminant is positive.
(D). This equation has 1 real solution because the discriminant is 0.
Answers
Answer:
d is the answer
Step-by-step explanation:
How long does it take a car to cover 200 km at a speed of 40 km h?
Answers
It would take a car 5 hours to cover 200 km at a speed of 40 km/h.
The car moves at a constant speed of 40 km/hr.
The car has to travel a total distance of 200 km.
As we know the formula of speed is distance/time,
Hence, s = d/t km/hr
So t = d/s hr
Let speed, distance and time be s, d, t respectively.
So by putting the values,
time t = 200/40 = 5 hours
Hence it can be said that the car would cover 200 km at the speed of 40 km/hr in 5 hours.
To learn more about speed visit: brainly.com/question/7359669
#SPJ4
Yves keeps track of the number of dinner guests at his home each night for one week. The data set is as follows: 12, 12, 12, 12, 12, 12, 12. What is the standard deviation of the scores
Answers
The standard deviation of the given data set, {12, 12, 12, 12, 12, 12, 12}, is zero. This is because the deviation of every value from the mean is zero. Therefore, the standard deviation of the given data set is zero.
In statistics, the standard deviation (SD) is a measure of how much the data is spread out from the mean, or how much the data deviates from the average value. It is calculated by finding the square root of the variance.Variance (σ2) is a measurement of the degree to which a set of data deviates from the mean. In other words, variance is a measure of how much the data is spread out. It is defined as the average of the squared differences from the mean.The formula for calculating the variance is
:σ2 = Σ(x - μ)2/N
where Σ represents the sum, x is the value of the observation,
μ is the mean of the observations, and
N is the total number of observations.
The standard deviation formula is the square root of the variance.
Therefore,σ = √σ2 = √Σ(x - μ)2/N
The given data set is {12, 12, 12, 12, 12, 12, 12}.
The mean of this data set is:(12+12+12+12+12+12+12) / 7 = 12
The deviation of every value from the mean is zero. Therefore, the variance of the given data set is zero. The standard deviation formula is the square root of the variance. Therefore, the standard deviation of the given data set is zero.
The standard deviation of the given data set, {12, 12, 12, 12, 12, 12, 12}, is zero.
To know more about standard deviation visit:
brainly.com/question/29115611
#SPJ11
Solve a = d+c/b
Help me please

Answers
Answer:
Option A is the correct
Step-by-step explanation:
a=d+c/b
Now we have to solve for d
Multiplying b on both sides
a*b=d+c/b*b
ab=d+c
ab-c=d
I hope this will help you:)
How do you solve the first line?

Answers
Answer:
18.84m
Step-by-step explanation:
The diameter=12m
To get the radius, the diameter has to be divided by 2
Radius=diameter/2
Radius=12/2=6m
Perimeter=3.14 x 6
=18.84m
plz help-
I don't wanna fail math-
again...

Answers
I hope this helps
Sebastian goes out to lunch. The bill, before tax and tip, was $8.75. A sales tax of 5% was added on. Sebastian tipped 17% on the amount after the sales tax was added. How much tip did he leave? Round to the nearest cent.
Answers
Answer:
1.56
Step-by-step explanation:
just do 8.75x1.05, then multiply that number by .17.
please mark as brainlest.
Million dollar bussyy jk help

Answers
Answer:
2. 2
3. 4
4. 3/4
5. 5/12
6. 6
7. 1/2
Ms. Reiger’s students found a total of 16 bird feathers. The line plot shows the lengths, in inches, of the bird feathers found by the students
Look at the line plot, and then select the two correct statements about the bird feathers.
The difference between the lengths of the shortest feather and the longest feather is 318 inches.
A. The difference between the lengths of the shortest feather and the longest feather is 238 inches.
B. The combined length of the two longest feathers is 828 inches.
C. The combined length of the shortest feather and the longest feather is 738 inches.
D. The combined length of the shortest feather and the longest feather is 618 inches.

Answers
Answer:
B
Step-by-step explanation:
The same amount of principal is invested in different accounts earning the same interest rate.
Which of the following accounts would have the greatest accumulated value at the end of one year?
A.An account eaming no interest
B.An account eaming simple interest
C.An account eaming interest compounded annually
D.An account earming interest compounded daily
Answers
Answer:
D.An account earming interest compounded daily
Step-by-step explanation:
An account earning interest compounded daily would have accumulated the greatest value at the end of the year.
Compound interest is interest on interest. In compound interest, the interest is calculated on the principal and interest accrued. This makes the value highest. For the account compounded daily, the interest on interest is taken every day. It has a power of 365. For compound interest accrued annually, the interest compounded yearly. Simple interest is basically on the principal.Answer: D! On edge 2021
Step-by-step explanation:
I just took the test :)
Find the value of x by solving the blue equation in the bottom.

Answers
If you solve this algebraically, this is what you would get. Hope this helps :)
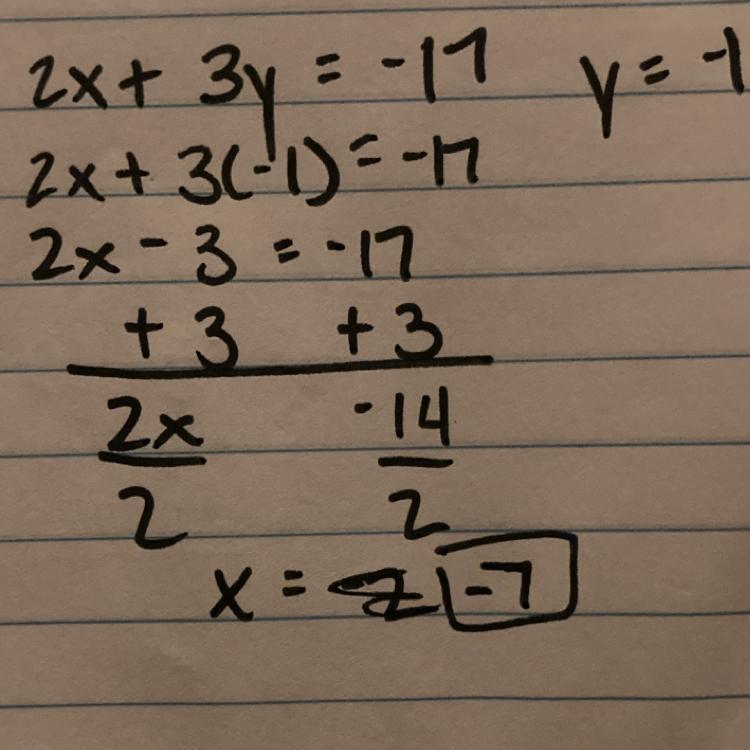
Find the scalar and vector projections of b onto a. a=⟨−5,12⟩, b=⟨4,6⟩
Answers
Step-by-step explanation:
The scalar projection of a vector b onto a vector a is given by the dot product of b and the unit vector of a:
p = (b · u) * u
where u is the unit vector of a, and can be found by dividing a by its magnitude:
u = a / ||a||
The vector projection of b onto a is simply the scalar projection scaled by the unit vector:
p = p * u
For the given vectors a = ⟨-5,12⟩ and b = ⟨4,6⟩, we first find the unit vector u:
u = a / ||a|| = ⟨-5,12⟩ / ||⟨-5,12⟩|| = ⟨-5/13,12/13⟩
Next, we find the dot product of b and u:
p = (b · u) = ⟨4,6⟩ · ⟨-5/13,12/13⟩ = (4 * -5/13) + (6 * 12/13) = -20/13 + 72/13 = 52/13
So the scalar projection of b onto a is p = 52/13.
Finally, we find the vector projection by scaling the unit vector u by the scalar projection:
p = p * u = (52/13) * ⟨-5/13,12/13⟩ = ⟨-52/169,104/169⟩
So the vector projection of b onto a is p = ⟨-52/169,104/169⟩.
Two parallel lines are cut by a transversal as shown below. Suppose m<1=34. Find m<6 and m<8
Answers
MULTIPLE CHOICE QUESTION
The REFLECTION of a point should ALWAYS be the SAME DISTANCE away from the opposite side of the line of reflection.
FALSE or TRUE?
Answers
Answer:
True
Step-by-step explanation:
A reflecrion always is the sam edustance because then it makes it look like they are reflecting each other.
find the nth derivative of each function by calculating the first few derivatives and observing the pattern that occurs.
Answers
The given function is solved using the power rule. The nth derivative of the given function f(x)=xⁿ is \(f^{(n)}(x) = n!x^{n-n }= n!\).
The power rule instructs how to differentiate xⁿ. It is used to determine the slope of polynomial functions as well as any other function with a real number exponent.
The given function is considered a power function. This is because the x is raised to the power (n). This n is considered a real number. So the derivative of this function is derived using the power rule.
First, differentiating the given function as follows,
\(\begin{aligned}f'(x)&=nx^{n-1}\\f''(x)&=n(n-1)x^{n-2}\\f'''(x)&=n(n-1)(n-2)x^{n-3}\end{aligned}\)
So observing the pattern, the nth derivative is found as follows, \(f^{(n)}(x) = n!x^{n-n }= n!\)
To know more about the power rule:
https://brainly.com/question/24920520
#SPJ4
The complete question is -
Find the nth derivative of each function by calculating the first few derivatives and observing the pattern that occurs.
f(x)=xⁿ
A backpack is on sale for 30% off. If the sales price is $15.75, what is the original price? Show your work.
Answers
Answer:
$22.50
Step-by-step explanation:
As it is 30% off, $15.75 is 70% of the full price. You can then divide 15.75 by 70 [= 0.225] to get 1% of the full price. Multiply 0.225 by 100 to get the full price. 0.225 x 100 = 22.5
We can check that this answer is correct by multiplying 22.50 by 0.7. If you get 15.75 you know the answer is correct as 15.75 is 70% of the full price.
define f : r 2 → r as: f(x1, x2) := { 0, if x1 is rational and x2 is irrational 1, otherwise show that f is discontinuous at each point of r 2 .
Answers
A system is characterized 4 x 10^-3 dy/dt+ 3y = 5 cos(1000t) - 10 cos(2000t). dt Determine y(t). (Hint: Apply the superposition property of LTI systems.) Answer(s) in Appendix F.
To know more about characterized refer here
https://brainly.com/question/30241716#
#SPJ11
Estimate the line of best fit using two points on the line.
A. y= -3/2x + 12
B. y= 3/2x + 12
C. y= -2/3 + 12
D. y= 2/3 + 12

Answers
Answer:
?
Step-by-step explanation:
Answer: c
Step-by-step explanation:
A p e x
- Andrew gave half of his money to support a local charity. From what was left, he spent
$22.75 on a present for his sister. If he had $183.89 left over, how much did he have to
begin with?
Answers
given 20 people, what is the probability that, among the 12 months in the year, there are 4 months containing exactly 2 birthdays and 4 containing exactly 3 birthdays?
Answers
the probability of having 4 months containing exactly 2 birthdays and 4 months containing exactly 3 birthdays among 20 people is approximately 0.000008, or about 0.0008%
The problem of calculating the probability of a certain pattern of birthdays among a group of people can be approached using the techniques of combinatorics and probability. To calculate the probability of having 4 months containing exactly 2 birthdays and 4 months containing exactly 3 birthdays among 20 people, we can use the following steps: First, we need to choose which 4 months will have exactly 2 birthdays and which 4 months will have exactly 3 birthdays. There are 12 months to choose from, so the number of ways to make these choices is given by the binomial coefficient: C(12, 4) × C(8, 4). This is the number of ways to choose 4 months out of 12 to have exactly 2 birthdays, multiplied by the number of ways to choose 4 months out of the remaining 8 to have exactly 3 birthdays. Next, we need to assign the people to the months. To do this, we can use the principle of inclusion-exclusion, which states that the number of ways to assign the people to the months so that each of the chosen months has the correct number of birthdays is: N = (20!/(2!²× 3!⁴)) × (4¹² - 6 × 3¹² + 4 × 2¹²). This expression counts the number of ways to distribute the 20 people among the 12 months so that the chosen months have the correct number of birthdays, and subtracts the cases where one or more of the chosen months have too many or too few birthdays. The factor (20!/(2!⁸ × 3!⁴)) accounts for the fact that we are counting distinguishable arrangements of people. Finally, we can calculate the probability of the desired pattern of birthdays by dividing the number of favorable outcomes (N) by the total number of possible outcomes, which is simply the total number of ways to assign the people to the months, given by: 12²⁰. Putting it all together, we get: P(4 months with 2 birthdays, 4 months with 3 birthdays) = N / 12²⁰. Evaluating this expression gives: P(4 months with 2 birthdays, 4 months with 3 birthdays) ≈ 0.000008. Therefore, the probability of having 4 months containing exactly 2 birthdays and 4 months containing exactly 3 birthdays among 20 people is approximately 0.000008, or about 0.0008%.
To learn more about probability click here
brainly.com/question/30034780
#SPJ4
Write the following as an algebraic expression. Simplify if possible.
Add 8y − 6 to 2y + 3.
The answer is ____.
Answers
Answer: 10y - 3
Step-by-step explanation:
We just add the "+" sign between the two.
So we get:
8y - 6 + 2y + 3
The y terms are like, so we do :
(8y + 2y) - 6 + 3
Which is:
10y - 6 + 3
The integers are like (common), so we do:
10y (-6 + 3)
Which is :
10y - 3
It is - 3 because -6 + 3 = -3, and we also add the "-" with the integer
So our final answer is=
10y - 3
Make my answer the brainliest!
Which expreion have a quotient of 6? Select all that apply. 0. 48 ÷ 0. 8
4. 8 ÷ 8
0. 48 ÷ 0. 08
4. 8 ÷ 0. 8
4. 8/0. 8
Answers
Expreion have a quotient of 6 is 0. 48 ÷ 0. 08.
What is quotient?
In mathematics, the quotient is the result of performing division operations on two integers. It is essentially the outcome of the division procedure. In arithmetic division, the terms divisor, dividend, quotient, and remainder are employed in four different ways.Division is one of the four basic operations of arithmetic, the ways that numbers are combined to make new numbers. The other operations are addition, subtraction, and multiplication.
0. 48 ÷ 0. 8
=0.06
The solution for Long Division of \($\frac{4.8}{8}$\) is 0.6
The solution for Long Division of \($\frac{0.48}{0.08}$\) is 6.
To learn more about Division visit:https://brainly.com/question/21416852
#SPJ4
I need help with my work

Answers
Answer:
1. acute angle (less than <90)
2. right angle (approximately <90)
3. obtuse angle (more than <90)
4. acute angle (less than <90)