If f(x) = -5x - 1, find the function value f(1).
f(1) =
Answers
Answer: f(1) = -6
Please mark me as Brainliest
Related Questions
can someone pls help w finding the x and y intercepts of this?
y=x^2-2x
Answers
Answer:
y-intercept is 0, x-intercept is 0 and 1
Step-by-step explanation:
For y-intercept, x=0 :
\({ \tt{y = {(0)}^{2} - 2(0) }} \\ { \tt{y = 0}}\)
For x-intercept, y=0 :
\({ \tt{0 = {2x}^{2} - 2x }} \\ { \tt{2x(x - 1) = 0}} \\ { \tt{x = 0 \: \: and \: \: 1}}\)
What can you triple and then subtract by 1 to get 29
Answers
Answer:
10 would be the answer :)
Simplify
a9/a5
a^4
1/a^4
4
a^14
Answers
Answer:
36a^10
Step-by-step explanation:
one half of negative five eights in numerical epression
Answers
Answer:
The answer is in the picture
Step-by-step explanation:
hope it helps!

50 plus 30 times 14 equalsss
Answers
Answer:
470 is your awnser
Step-by-step explanation:
Answer:
50 + 30 * 14 = 470
Step-by-step explanation:
50 + 30 * 14
= 50 + 420
= 470
What is the answer Which of the following equations have infinitely many solutions?
Choose all answers that apply:
Choose all answers that apply:
(Choice A)
A
-6x+35=-6x-35−6x+35=−6x−35minus, 6, x, plus, 35, equals, minus, 6, x, minus, 35
(Choice B)
B
6x+35=-6x-356x+35=−6x−356, x, plus, 35, equals, minus, 6, x, minus, 35
(Choice C)
C
-6x+35=-6x+35−6x+35=−6x+35minus, 6, x, plus, 35, equals, minus, 6, x, plus, 35
(Choice D)
D
6x+35=-6x+356x+35=−6x+35
I am still confused
Answers
-6x+35 = -6x+35 has the same thing on each side: , so this has infinite solutions. Option c is correct.
An equation will have infinite solutions if both sides of the equal sign are the exact same thing, for instance . (You can test this with any value of x and find that they all work!)
So to find the equations that have infinite solutions, we need to see which have the same exact sides.
(Choice A)
-6x+35 = -6x-35 have the different thing on each side: , so this has no solution.
(Choice B)
6x+35 = -6x-35 does not have the same thing on each side, so it doesn’t have infinite solutions (it has 1).
(Choice C)
-6x+35 = -6x+35 has the same thing on each side: , so this has infinite solutions.
(Choice D)
6x+35=-6x+35 And finally, has the different thing on each side: , so it has one solution.
Hence , -6x+35 = -6x+35 has the same thing on each side: , so this has infinite solutions.
Learn more about infinite solutions at:
https://brainly.com/question/27927692
#SPJ1
how does one do this equasion 6234653928+294292342-424624642x16515615615165161x1156+6466456
Answers
The given Expression simplifies to -8.1069556e+27
What is BODMAS rule?BODMAS stands for Bracket, Of, Division, Multiplication, Addition, and Subtraction. A mathematical expression's order of execution is explained using the BODMAS.
Given an equation to solve,
6234653928 + 294292342 - 424624642 x 16515615615165161 x 1156 + 6466456
Let us consider this Expression as A + B - C * D * E + F, with the corresponding terms being equal
By, the BODMAS rule,
First step: Multiply C, D, E. Let this be G
Now, the equation will look like this: A + B - G + F
Second step: We can add and subtract according to the signs now
On solving, the expression simplifies to -8.1069556e+27
To learn more about BODMAS, refer to the link below:
https://brainly.com/question/29626866
#SPJ1
the least squares regression line for a data set is yˆ=2.3−0.1x and the standard deviation of the residuals is 0.13. does a case with the values x = 4.1, y = 2.34 qualify as an outlier?
- Cannot be determined with the given information
- Yes
- No
Answers
Therefore, the correct option is "Cannot be determined with the given information." when the least squares regression line for a data set is y=2.3−0.1x and the standard deviation of the residuals is 0.13.
To determine if a case with the values x = 4.1, y = 2.34 qualifies as an outlier, we need to compare the observed value of y (2.34) with the predicted value of y based on the regression line (Y).
For this case, the predicted value of y (Y) can be calculated using the equation of the least squares regression line:
Y = 2.3 - 0.1x
Y = 2.3 - 0.1 * 4.1
Y = 2.3 - 0.41
Y = 1.89
Now, we can compare the observed value of y (2.34) with the predicted value of y (1.89). If the observed value significantly deviates from the predicted value, it can be considered an outlier.
In this case, the observed value (2.34) is greater than the predicted value (1.89), suggesting that it is above the regression line. However, without knowing the specific criteria or threshold for defining an outlier, it cannot be conclusively determined if this case qualifies as an outlier based solely on the information given.
To know more about least squares regression line,
https://brainly.com/question/29463195
#SPJ11
Prove each of these identities.
a (1 + secx) (cosec x - cotx) = tan x
b (1 + sec x)(1 - cos x) = sin x tan x
Answers
➲ ( 1 + sec x )( cosec x - cot x ) = tan x
Solving for L.H.S\( \implies\quad \sf{(1+sec\:x)(cosec\:x-cot\:x) }\)
\( \implies\quad \sf{ \left(1+\dfrac{1}{cos\:x}\right)\left(\dfrac{1}{sin\:x}-\dfrac{cos\:x}{sin\:x}\right)}\)
\( \implies\quad \sf{ \left(\dfrac{1+cos\:x}{cos\:x}\right)\left(\dfrac{1-cos\:x}{sin\:x}\right)}\)
\( \implies\quad \sf{ \left(\dfrac{1-cos^2 x}{cos\:x.sin\:x}\right)}\)
\( \implies\quad \sf{ \left( \dfrac{sin^2 x}{cos\:x.sin\:x}\right)}\)
\( \implies\quad \sf{ \left( \dfrac{sin\:x.\cancel{sin\:x}}{cos\:x.\cancel{sin\:x}}\right)}\)
\( \implies\quad \sf{\left( \dfrac{sin\:x}{cos\:x}\right) }\)
\( \implies\quad\underline{\underline{\pmb{ \sf{tan\:x}}} }\)
➲ ( 1+ sec x )( 1- cos x ) = sin x. tan x
Solving for L.H.S\( \implies\quad \sf{ ( 1+ sec\:x)(1-cos\:x)}\)
\( \implies\quad \sf{\left(1+\dfrac{1}{cos\:x} \right) \left( 1-cos\:x\right)}\)
\( \implies\quad \sf{ \left(\dfrac{cos\:x+1}{cos\:x} \right)(1-cos \:x)}\)
\( \implies\quad \sf{\dfrac{1-cos^2 x}{cos\:x} }\)
\( \implies\quad \sf{\dfrac{sin^2x}{cos\:x} }\)
\( \implies\quad \sf{sin\:x.\left( \dfrac{sin\:}{cos\:x}\right) }\)
\( \implies\quad\underline{\underline{\pmb{ \sf{sin\:x.tan\:x}}} }\)
6. An ant travels at a constant rate of 30 cm every 2 minutes.-
a. At what pace does the ant travel per centimeter?
b. At what speed does the ant travel per minute?
(From Unit 2, Lesson 18.)
Answers
A:
4 seconds per centimer:
30cms 15 cms
---------------- -------------
2 minutes 1 minute
1 minute= 60 seconds
15 cms 1cm
----------------- = ----------------
60 seconds 4seconds
B: 15 cms per minute
30cms/2minutes
(divide by 2 to get speed for one minute)
15cm/1 minute
The graph of the function g(x) = -x is shown on the grid below.Graph the function h(x) = -x +2+3 in the interactive graph.←++-9-8-7-6-5-4-3-28886103219Y7+6+5+4+3.2.-2--3+-4+-5+-6+$7-8+69-9.2 3 4 5 6 7 8 9y= g(x)→x

Answers
Given:
Given a graph of the function
\(g(x)=-|x|\)Required:
To graph the function
\(h(x)=-|x+2|+3\)Explanation:
The graph of the function h(x) is,
The blue graph is the graph of the function h(x).
Final Answer:


Kayla rolls a die 84 times. How many times can she expect to roll a 3?
A. 14
B. 21
C. 12
D. 18
Answers
Answer:
\(\huge\boxed{\sf 14\ times}\)
Step-by-step explanation:
Formula:\(\displaystyle Probability = \frac{Possible \ no. \ of\ events}{Total \ number\ of \ events}\)
Solution:If we roll a die 1 time, the probability of obtaining a 3 is:
= 1 / 6
Because a die has total 6 faces, out of which 3 is only 1.
But, if we roll it 84 times, it becomes:
= \(\displaystyle \frac{1}{6} \times 84\)
= 84/6
= 14 times\(\rule[225]{225}{2}\)
A test used to determine whether or not first-order autocorrelation is present is _____ test.
a. chi-square
b. t
c. Durbin-Watson
d. serial-autocorrelation
Answers
The test used to determine whether or not first-order autocorrelation is present is the Durbin-Watson test.
1. Fit a regression model to the data.
2. Obtain the residuals, which represent the differences between the observed values and the predicted values from the regression model.
3. Calculate the Durbin-Watson statistic, which is a ratio of the sum of squared differences between adjacent residuals to the sum of squared residuals.
4. Compare the calculated Durbin-Watson statistic to critical values from a Durbin-Watson table or use statistical software to determine if there is significant autocorrelation.
5. The Durbin-Watson statistic ranges from 0 to 4, where a value around 2 suggests no autocorrelation, a value below 2 indicates positive autocorrelation, and a value above 2 indicates negative autocorrelation.
6. By analyzing the Durbin-Watson statistic, researchers can make conclusions about the presence or absence of first-order autocorrelation in the regression model.
Learn more about sum : brainly.com/question/31538098
#SPJ11
PLEASE HELPPPPPPPP!!!!

Answers
Answer:
See below ~
Step-by-step explanation:
1.
x² + y² + 14x - 2y = -1[x² + 14x + 49] - 49 + [y² - 2y + 1] - 1 = -1(x + 7)² + (y - 1)² = 49Centre = (x, y) = (-7, 1)Radius = √49 = 72.
x² + y² - 10x + 8y - 8 = 0[x² - 10x + 25] - 25 + [y² + 8y + 16] - 16 - 8 = 0(x - 5)² + (y + 4)² = 49Centre = (x, y) = (5, -4)Radius = √49 = 73.
Points are : (-2, 1) and (4, 3)D = √(4 + 2)² + (3 - 1)²D = √36 + 4D = √40D = 2√10find the area under the standard normal curve over the interval specified below to the right of z=3
Answers
The standard normal curve, also known as the standard normal distribution or the z-distribution, is a specific probability distribution that follows a bell-shaped curve. The area under the standard normal curve to the right of z = 3 is approximately 0.0013.
For the area under the standard normal curve to the right of z = 3, we need to calculate the cumulative probability from z = 3 to positive infinity.
The standard normal distribution, also known as the z-distribution, has a mean of 0 and a standard deviation of 1. It is a symmetric bell-shaped curve that represents the distribution of standard scores or z-scores.
Using statistical tables or software, we can find the cumulative probability associated with z = 3, which represents the area under the curve to the left of z = 3.
The cumulative probability for z = 3 is approximately 0.9987.
For the area to the right of z = 3, we subtract the cumulative probability from 1.
Therefore, the area to the right of z = 3 is approximately 1 - 0.9987 = 0.0013.
In conclusion, the area under the standard normal curve to the right of z = 3 is approximately 0.0013.
This means that the probability of randomly selecting a value from the standard normal distribution that is greater than 3 is approximately 0.0013 or 0.13%.
To know more about standard normal curve refer here:
https://brainly.com/question/31666967#
#SPJ11
Identify the interquartile range for the set of values below. 37, 34 , 29 , 33, 35 , 30 , 34 A) 4 B) 5 C) 3 D) 8
Answers
Answer:25th Percentile: 5
50th Percentile: 30
75th Percentile: 34
Interquartile Range: 29
Step-by-step explanation:
Answer:
it is 5
Step-by-step explanation:
i looked it up
Sophie can type 129 words in 3 minutes. How many minutes will it take her to type 559 words?
Answers
EXPLANATION:
To solve the exercise we must make a rule of three.
The exercise is as follows:
\(\begin{gathered} 129\text{ }words\text{ }\rightarrow3\text{ minutes} \\ 559\text{ words}\rightarrow x \\ \frac{559\times3}{129}=13\text{ minutes} \\ \text{the answer is 13minutes} \end{gathered}\)(-2,1),(2,-5) slope intercept form
Answers
Answer:
y = -3/2 x -2Step-by-step explanation:
The equation of a line in slope-intercept form is expressed as y = mx+b
m is the slope
b is the intercept
Get the slope
m = -5-1/2-(-2)
m = -6/4
m = -3/2
Get the intercept
Substitute m = -3/2 and (-2, 1) into y = mx+c
1 = -3/2(-2) + c
1 = 3 + c
c = 1-3
c =-2
Get the required equation
y = mx+c
y = -3/2 x + (-2)
y = -3/2 x -2
Hence the required equation is y = -3/2 x -2
A Sample Has A Density Of 7.9 X 109 CFU/ML. What Sample Volume Should Yield A Countable Plate? 1 ML Of A 10-8 Original
Answers
To plate 1 mL of a sample that has been diluted in 0.00000001 mL of diluent, or a dilution factor of 10^8.
To determine what sample volume should yield a countable plate, we need to calculate the appropriate dilution factor.
The sample has a density of 7.9 x 10^9 CFU/mL, and we want to plate 1 mL of a 10^-8 original dilution, which means we need to dilute the sample by a factor of 10^8 to obtain a countable plate.
We can calculate the required dilution factor using the following formula:
Dilution factor = (Volume of sample plated) / (Total volume of diluted sample)
To dilute the sample by a factor of 10^8, we can calculate the total volume of diluted sample as follows:
Total volume of diluted sample = (Volume of sample plated) x (Dilution factor)
Substituting the values, we get:
10^8 = 1 mL / (Total volume of diluted sample)
Total volume of diluted sample = 1 mL / 10^8
Total volume of diluted sample = 0.00000001 mL
Therefore, to obtain a countable plate, we need to plate 1 mL of a sample that has been diluted in 0.00000001 mL of diluent, or a dilution factor of 10^8.
Learn more about dilution factor here
https://brainly.com/question/31503152
#SPJ11
find the centroid ( ¯ x , ¯ y ) of the triangle with vertices at ( 0 , 0 ) , ( 5 , 0 ) , and ( 0 , 7 ) .
Answers
The centroid of a triangle is the point where the three medians of the triangle intersect. In this case, the triangle has vertices at (0, 0), (5, 0), and (0, 7).
First, let's calculate the average x-coordinate:
¯x = (0 + 5 + 0) / 3 = 5/3 ≈ 1.67
Next, let's calculate the average y-coordinate:
¯y = (0 + 0 + 7) / 3 = 7/3 ≈ 2.33, the centroid of the triangle with vertices at (0, 0), (5, 0), and (0, 7) is approximately (1.67, 2.33).
In summary, the centroid of the triangle with verticesvertices at (0, 0), (5, 0), and (0, 7) is located at approximately (1.67, 2.33). This point represents the average position of the three vertices and is the intersection point of the medians of the triangle.
The centroid coordinates are found by taking the average of the x-coordinates and the average of the y-coordinates of the three vertices. In this case, we add up the x-coordinates (0 + 5 + 0 = 5) and divide by 3 to get an average of 5/3, which is approximately 1.67. Similarly, we add up the y-coordinates (0 + 0 + 7 = 7) and divide by 3 to get an average of 7/3, which is approximately 2.33. These values represent the x-coordinate (¯x) and the y-coordinate (¯y) of the centroid, respectively. Therefore, the centroid of the triangle is located at approximately (1.67, 2.33).
Learn more about triangles here
brainly.com/question/14366937
#SPJ11
Skylar just got hired for a new job and will make $61,000 in her first year. Skylar was told that she can expect to get raises of $2,500 every year going forward. How much money in salary would Skylar make in her 6th year working at this job?
Answers
If f(x) is given as an equation and g(x) is given as a table, how i can tell they are inverses
Answers
Answer: f(x) and g(x) both represent y of the equations
Step-by-step explanation: f(x) and g(x) both represent the y of the equation for example f(x)=mx+b or g(x)+mx+b both would be to find y of that specific equation and that would also make them inverses because you could use the table to label the inverses on a graph.
The proportion of a normal distribution located between z = .50 and z = -.50 is ____.
Answers
The proportion of a normal distribution located between z = .50 and z = -.50 will be 38.2%.
We have,
A normal distribution located between z = 0.50 and z = -0.50,
So,
Now,
From the Z-score table,
We get,
The Probability corresponding to the Z score of -0.50,
i.e.
P(-0.50 < X < 0) = 0.191,
And,
The Probability corresponding to the Z score of -0.50,
i.e.
P(0 < X < 0.50) = 0.191,
Now,
The proportion of a normal distribution,
i.e.
P(Z₁ < X < Z₂) = P(Z₁ < X < 0) + P(0 < X < Z₂)
Now,
Putting values,
i.e.
P(-0.50 < X < 0.50) = P(-0.50 < X < 0) + P(0 < X < 0.50)
Now,
Again putting values,
We get,
P(-0.50 < X < 0.50) = 0.191 + 0.191
On solving we get,
P(-0.50 < X < 0.50) = 0.382
So,
We can write as,
P(-0.50 < X < 0.50) = 38.2%
So,
The proportion of a normal distribution is 38.2%.
Hence we can say that the proportion of a normal distribution located between z = .50 and z = -.50 will be 38.2%.
Learn more about normal distribution here
https://brainly.com/question/13759327
#SPJ4
The demand equation for a product is p = 29 -0.01q
Write the revenue as a function of q and find the qunatity that maximizes revenue
R(q) =
The quantity that maximizes revenue is _____________________
The price of each item at this production level is $________________
The total revenue at this price is $_______________________
Answers
The quantity that maximizes revenue is 1450.
The price of each item at this production level is $14.50.
The total revenue at this price is $21,025.
The revenue as a function of q can be found by multiplying the price (p) by the quantity (q):
R(q) = pq = q(29 - 0.01q) = 29q - 0.01q^2
To find the quantity that maximizes revenue, we take the derivative of R(q) with respect to q and set it equal to zero:
R'(q) = 29 - 0.02q = 0
0.02q = 29
q = 1450
Therefore, the quantity that maximizes revenue is 1450.
To find the price at this production level, we substitute q = 1450 into the demand equation:
p = 29 - 0.01(1450) = $14.50
So the price of each item at this production level is $14.50.
The total revenue at this price can be found by substituting q = 1450 and p = $14.50 into the revenue equation:
R(1450) = 1450(14.50) = $21,025
To learn more about the demand function visit : https://brainly.com/question/24384825
#SPJ11
Which of the equations are true identities? \begin{aligned} \text{A. }&(y+6)(y-7)+42=y^2-y \\\\ \text{B. }&(x+3)(x-8)=x^2-5x \end{aligned} A. B. (y+6)(y−7)+42=y 2 −y (x+3)(x−8)=x 2 −5x
Answers
Answer:
Only A, the first equation is true.
Step-by-step explanation:
A. (y + 6)(y – 7) + 42 = y² + 6y –7y – 42 + 42 = y² – y. This means A is true
B. (x + 3)(X – 8) = x² + 3x – 8x – 24 = x² – 5x – 24. This means B is false.
what isle is the tattoo ink in walmart???
Answers
Answer: what
Step-by-step explanation:
6.549, 13/2, 6 6/11, 6.77 least to greatest
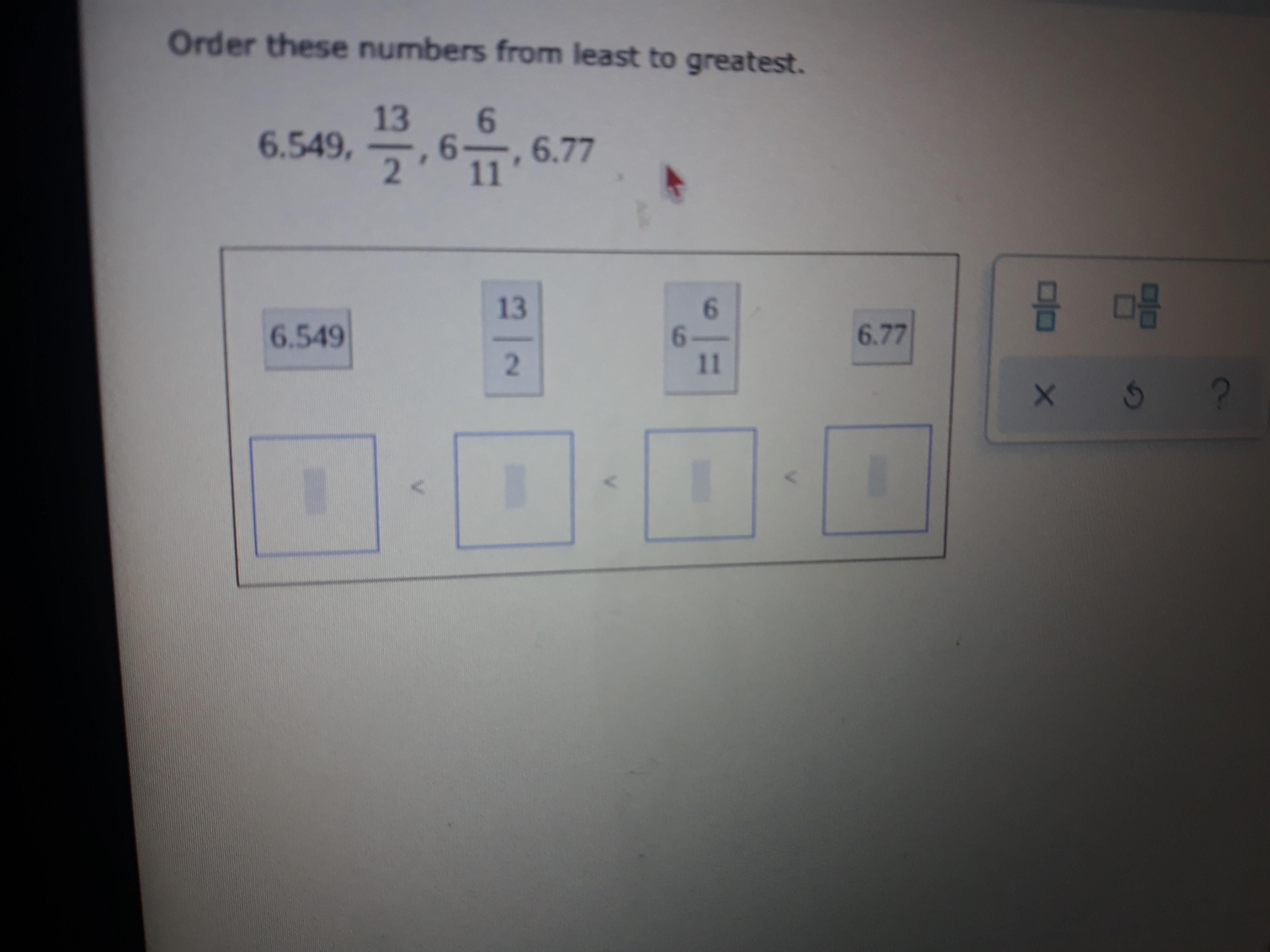
Answers
Answer:
13/2, 6.549, 6 6/11, 6.77
15 points Need ASAP- Use the table to write a proportion ~ (table on pic)

Answers
Answer:
m=24
Step-by-step explanation:
Andrew owns fewer DVDs than Paul. Let k represent the number of Paul's DVD. Identify the expression that can be used to find the number of DVD that Andrew owns.
Answers
Question:
Andrew owns 3 fewer DVDs than Paul. Let K represent the number of Paul's DVDs. Write the expression that can be used to find the number of DVDs that Andrew owns.
Answer:
\(Andrew = k - 3\)
Step-by-step explanation:
Given
\(Paul = k\)
\(Andrew = 3\ fewer\)
Required
Write an expression for Andrew
3 fewer means that we subtract 3 from Paul's number of DVDs.
i.e.
\(Andrew = Paul - 3\)
Substitute k for Paul
\(Andrew = k - 3\)
You paint 1/2 wall in 1/4 hour. At that rate, how long will it take you to paint one wall?
Answers
Answer:
40 minutes is your answer
Answer: It will take a 1/2 hour or 30min to paint one full wall.