Answers
Answer: 260 m
Step-by-step explanation:
Let's say the length of NR is x m, using the similarity rule, we get the equation
175/130 = (175+175)/x
x = 260
So NR is 260 m
Related Questions
What probability that when I draw two cards from a standard 52 card deck, that the first one is a queen and the second one is a heart, given that I do not replace the first card?
Answers
The probability of drawing a queen first and then a heart second without replacement is 1/51.
How do we calculate the probability?In this case, the probability of drawing a queen first and then a heart second is:
P(Queen and Heart) = P(Queen) * P(Heart | Queen)
The probability of drawing a queen first is 4/52, since there are 4 queens in a standard deck of 52 cards. The probability of drawing a heart second, given that a queen has already been drawn, is 13/51, since there are 13 hearts in the deck and now only 51 cards remaining after the first draw.
Therefore, the probability of drawing a queen first and then a heart second without replacement is:
P(Queen and Heart) = (4/52) * (13/51) = 52/2652 = 1/51
So the probability of drawing a queen first and then a heart second without replacement is 1/51.
See more about probability at: https://brainly.com/question/24756209
#SPJ11
a company randomly selects 100 light bulbs every day for 40 days from its production process. if 600 defective light bulbs are found in the sampled bulbs then the estimate for the average percent defective would be:
Answers
the estimated average percent defective for the sampled bulbs is 6%.
Calculate the total number of bulbs sampled: 100 bulbs x 40 days = 4000 bulbs.
Calculate the percent defective: 600 defective bulbs/4000 total bulbs x 100 = 6%.
A company randomly sampled 100 light bulbs from its production process every day for 40 days. By the end of the 40 days, a total of 4000 light bulbs were sampled. Out of the 4000 bulbs, 600 were found to be defective. This means that the average percent defective is 6%. This can be calculated by dividing the number of defective bulbs (600) by the total number of bulbs sampled (4000) and multiplying by 100. Therefore, the estimated average percent defective for the sampled bulbs is 6%.
Learn more about average here
https://brainly.com/question/24057012
#SPJ4
cylinder container has a radius of 3 in. and a height of 12 in. The
cylinder contains 25 spherical balls that have a diameter of 1.5 in. About
how much space is left in the container not including the balls?
Answers
There is about 295.11335 cubic inches of space left in the container, not including the balls.
We must first determine the cylinder's total volume before deducting the volume of the 25 spheres in order to determine the amount of space still inside the container.
The formula for calculating a cylinder's volume is V_cylinder = * r2 * h, where V_cylinder denotes the cylinder's volume, r stands for the cylinder's radius, and h denotes the cylinder's height.
The cylinder's radius (r) in this instance is specified as 3 inches, while its height (h) is specified as 12 inches. We may determine the volume of the cylinder by entering these values into the formula.
V_cylinder equals 3.14159 * 3 2 * 12 V_cylinder is 339.292 in3 in volume.
Next, we must determine the volume of each sphere. The following equation determines a sphere's volume:
Where: V_sphere = (4/3) * * (r3) V_sphere is the sphere's volume, is a mathematical constant roughly equal to 3.14159, and r is the sphere's radius.
The spherical balls' diameter (d) in this instance is 1.5 inches, which means the radius (r) is equal to half of the diameter.
r = 1.5/2d/2 = 0.75 inches.
We may get the volume of each spherical ball using this value as a plug-in in the formula.
V_sphere is equal to 4.33 * 3.14159 * 0.75.
1.7671459 in3 V_sphere
The volume of one sphere is multiplied by the quantity of spheres in order to determine the combined volume of the 25 spherical balls.
V_total_spheres is calculated as V_sphere * 25 V_total_spheres 44.17865 in3.
Finally, we can determine how much room is still in the container by deducting the volume of the 25 spheres from the cylinder's volume.
Space left is equal to V_cylinder - V_total_spheres.
339.292 - 44.17865 space_left
295.11335 in3 of space is remaining.
Without accounting for the balls, there is approximately 295.11335 cubic inches of empty space in the container.
For more such questions on space , Visit:
https://brainly.com/question/29719992
#SPJ11
can someone help me please

Answers
Answer:
C. d = C/pi
Step-by-step explanation:
lol nothing really to explain but it's saying diameter equals circumference divided by pi
Hope this helps dude !
Assume that random guesses are made for eight multiple choice questions on an SAT test, so that there are n 8 trials, each with probability of success (correct) given by p 0.45. Find the indicated probability for the number of correct answers. Find the probability that the number x of correct answers is fewer than 4. P(X< 4) (Round to four decimal places as needed.)
Answers
Probability for the number of correct answers is fewer than 4 is 0.3993.
The probability that the number x of correct answers is fewer than 4 can be found using the binomial probability formula:
P(X = x) = (n choose x) * p^x * (1-p)^(n-x)
Where n is the number of trials, x is the number of successes, and p is the probability of success.
For this problem, n = 8, p = 0.45, and we want to find P(X < 4).
To find P(X < 4), we need to find the probability of 0, 1, 2, and 3 correct answers and add them together:
P(X < 4) = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
Using the binomial probability formula, we can find each of these probabilities:
P(X = 0) = (8 choose 0) * 0.45^0 * (1-0.45)^(8-0) = 0.0059
P(X = 1) = (8 choose 1) * 0.45^1 * (1-0.45)^(8-1) = 0.0416
P(X = 2) = (8 choose 2) * 0.45^2 * (1-0.45)^(8-2) = 0.1275
P(X = 3) = (8 choose 3) * 0.45^3 * (1-0.45)^(8-3) = 0.2243
Adding these probabilities together, we get:
P(X < 4) = 0.0059 + 0.0416 + 0.1275 + 0.2243 = 0.3993
Therefore, the probability that the number x of correct answers is fewer than 4 is 0.3993.
Learn more about probability at https://brainly.com/question/15063997
#SPJ11
What is the equation of the line that passes through the point
(
4
,
1
)
(4,1) and has a slope of
1
2
2
1
?
Answers
The equation of the line that passes through the point (3, 4) with a slope of 2 is y = 2x - 2.
To determine the equation of a line that passes through a given point, it is necessary to have at least one additional point on the line or the slope of the line. Once this information is obtained, the point-slope form of a linear equation can be used to find the equation of the line that passes through the given point.
A linear equation can be expressed in slope-intercept form
(y = mx + b)
or in point-slope form
(y - y1 = m(x - x1))
. The point-slope form of the equation of a line is useful when given a point and a slope. However, if the slope of the line is not given, the point-slope form is more appropriate.Let's assume that the line passes through the point (a, b) and has slope m. Using the point-slope form of the equation of a line, the equation can be written as:y - b = m(x - a)Expanding the equation, we get:
y - b = mx - ma
Rearranging, we get:
y = mx - (ma + b)
Therefore, the equation of the line that passes through the given point is y = mx - (ma + b), where m is the slope of the line.
Let's take an example. If a line passes through the point (3, 4) and has a slope of 2, the equation of the line can be found using the point-slope form as:y - 4 = 2(x - 3)Expanding:
y - 4 = 2x - 6y = 2x - 2
For such more question on equation
https://brainly.com/question/29174899
#SPJ8
What is the median of the data set?
{7, 4, 2, 0, 12, 7,3}
Select from the drop-down menu to correctly complete the statement.
The median of the data set is Choose... 0, 4, 5, 7, 12
Answers
Answer:
4
Step-by-step explanation:
To find the median (middle) of the data set, first arrange the numbers in order: 0, 2, 3, 4, 7, 7, 12. Now find the middle number: 4.
Hope it helps!
Answer:
4
Step-by-step explanation:
p l e a s e h e l p p p p !!!

Answers
Answer:
This would be the last option I think, sorry if it's wrong.
Step-by-step explanation:
Answer:last option
Step-by-step explanation:
help needed! please and thank uuu! no links please!

Answers
Answer:
(2x×3x)+(3x×-3)
Area=L×W
Blue rectangle = 2x×3x
Pink rectangle = 3x×-3
(2x×3x)+(3x×-3)
WILL GIVE BRAINLIEST (08.03) Consider the following pair of equations:
y = 3x + 3
y = x − 1
Explain how you will solve the pair of equations by substitution. Show all the steps and write the solution in (x, y) form.
Answers
Answer:
(- 2, - 3 )
Step-by-step explanation:
y = 3x + 3 → (1)
y = x - 1 → (2)
substitute y = 3x + 3 into (2)
3x + 3 = x - 1 ( subtract x from both sides )
2x + 3 = - 1 ( subtract 3 from both sides )
2x = - 4 ( divide both sides by 2 )
x = - 2
substitute x = - 2 into either of the 2 equations and evaluate for y
substituting into (2)
y = - 2 - 1 = - 3
solution is (- 2, - 3 )
Answer:
y = -3, x = -2
Step-by-step explanation:
1. Substitute "y = x - 1" in for y in the first equation:
x - 1 = 3x + 3
2. Isolate x:
x = 3x + 3 + 1
3. Combine like terms:
-2x = 4
4. Solve for x:
-2x/-2 = 4/-2
x = -2
5. Solve for y with substitution (using the second equation):
y = -2 - 1
y = -3
hope this helps!
Jaylin solved this equation from the card sort:
15 – 7x= 3 + 5x
12 – 7x= 5x
12 = 12x
1= x
Is this correct?
Answers
-g -24= -17
What is the answer ?
Answers
Answer:
g = -7
I hope this helps!
what involves asking questions and answering those questions using statistical and quantitative tools for explanatory and predictive analysis?
Answers
A process of analysing, purifying, manipulating, and modelling data in order to find relevant information, come to conclusions, and enhance decision-making is known as data analytics.
It entails posing queries and providing answers utilising quantitative and statistical methods for explanatory and prescriptive analysis. Descriptive, diagnostic, predictive, and prescriptive analytics are the four basic categories of data analysis.
Diagnostic analytics is used to determine the reason why something occurred, whereas descriptive analytics is used to report what has already occurred.
The use of predictive analytics, on the other hand, enables the prediction of likely future events. Last but not least, prescriptive analytics is employed to decide what steps should be taken in order to accomplish a particular result or goal in light of the knowledge gleaned from descriptive, diagnostic, and predictive analytics.
By using these different types of analytics, individuals will be able to gather and analyze data to better understand trends, identify problems, and make informed decisions.
Know more about Data analytics here:
https://brainly.com/question/32575972
#SPJ11
Write a quadratic equation in standard form with \(\frac{3}{4}\) an -5 as its roots
Answers
Knowing the roots first write the equation in factored form:
(X - 3/4)(x +5) = 0
Now use the FOIL method ( multiply each term in one set of parentheses by each term the other set:
X•x + x•5 -3/4•x -3/4•5
Simplify:
X^2 + 5x -3/4x -3 3/4
Combine like terms:
X^2+ 4 1/4x - 3 3/4
two parallel lines are crossed by a transversal.

Answers
Answer:
\({ \boxed{ \tt{m \angle1 = m \angle5}}} \\ { \tt{m \angle1 = 180 \degree - m \angle6}} \\ { \tt{m \angle1 = 180 \degree - 123.5 \degree}} \\ { \bf{m \angle1 = 56.5 \degree}}\)
When a pair of parallel lines is intersected by a transversal, then
Corresponding angles are equal.
∠2 and ∠6 are corresponding angles.
So, m∠2 = m∠6
=> m∠2 = 123.5°
We know that linear pair of angles are supplementary (180°).
∠1 and ∠2 are linear pair of angles.
So, m∠1 + m∠2 = 180°
=> m∠1 + 123.5° = 180°
=> m∠1 = 180° - 123.5°
=> m∠1 = 56.5°
What numbers must you know to find the surface area and volume of a sphere?
A) The sphere's radius and the circumference and area of a great circle
B) The sphere's radius and the circumference of a great circle
C) The sphere's radius
D)The sphere's radius and the area of a great circle
Answers
Answer: c) sphere's radius
Step-by-step explanation:
formula for volume of sphere = \(\frac{4}{3} \pi r^{3}\)
formula for surface area of sphere = 4πr²
we need to know the radius of sphere to find both
the average monthly residential gas bill for black hills energy customers in cheyenne, wyoming is (wyoming public service commission website). how is the average monthly gas bill for a cheyenne residence related to the square footage, number of rooms, and age of the residence? the following data show the average monthly gas bill for last year, square footage, number of rooms, and age for typical cheyenne residences. average monthly gas number of bill for last year age square footage rooms $70.20 16 2537 6 $81.33 2 3437 8 $45.86 27 976 6 $59.21 11 1713 7 $117.88 16 3979 11 $57.78 2 1328 7 $47.01 27 1251 6 $52.89 4 827 5 $32.90 12 645 4 $67.04 29 2849 5 $76.76 1 2392 7 $60.40 26 900 5 $44.07 14 1386 5 $26.68 20 1299 4 $62.70 17 1441 6 $45.37 13 562 4 $38.09 10 2140 4 $45.31 22 908 6 $52.45 24 1568 5 $96.11 27 1140 10 a. develop an estimated regression equation that can be used to predict a residence's average monthly gas bill for last year given its age. round your answers to four decimals.
Answers
An estimated regression equation that can be used to predict a residence's average monthly gas bill for last year given its age is \($\hat{y} = 115.14 - 3.167x$\). The average monthly gas bill for last year increases by $0.2456 on average.
Using age as the predictor variable and average monthly gas bill as the response variable, we can use linear regression to develop an estimated regression equation:
\($\hat{y} = b_0 + b_1 x$\)
where \(\hat{y}\) is the predicted average monthly gas bill, x is the age of the residence, b₀ is the intercept and b₁ is the slope.
Using the given data, we can find the values of b₀ and b₁:
\($\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i = 17.6$\)
\($\bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_i = 55.906$\)
\($s_x = \sqrt{\frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n-1}} = 8.564$\)
\($s_y = \sqrt{\frac{\sum_{i=1}^{n} (y_i - \bar{y})^2}{n-1}} = 24.193$\)
\($r = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n} (x_i - \bar{x})^2} \sqrt{\sum_{i=1}^{n} (y_i - \bar{y})^2}} = -0.577$\)
\($b_1 = r \frac{s_y}{s_x} = -3.167$\)
\($b_0 = \bar{y} - b_1 \bar{x} = 115.14$\)
Therefore, the estimated regression equation is:
\($\hat{y} = 115.14 - 3.167x$\)
where \(\hat{y}$\) is the predicted average monthly gas bill and x is the age of the residence.
This equation suggests that as the age of the residence increases by one year, the average monthly gas bill for last year increases by $0.2456 on average.
Learn more about regression equation here:
brainly.com/question/17079948
#SPJ11
2x-y=2 4x+y=4 express each solution as an ordered pair
Answers
Answer: 2x-y=2= y=−2x+2
4x+y=4= y=-4x+4
Step-by-step explanation:
Answer: if you Solve by Substitution you get (point form: (1, 0)
(equation form: x = 1, y = 0)
Step-by-step explanation:
Solve for the first variable in one of the equations, then substitute the result into the other equation.
Solve for x:
y = −4x + 4
y = 2x − 2

A client pays for a moving company to move 25 boxes. If the moving company charges $12.50 per box and a base fee of $199.95 to each client, what is the total amount the client pays? S212.45 $237.15 $312.50 $512.-15
Answers
Answer:
$512.45Step-by-step explanation:
Total payment to each client comprises of the base fee and the fee for moving boxes:
199.95 + 25*12.50 = 512.45Total amount is $512.45
My tv has a length of 78.4 inches and a width of 44.1 inches. If I wanted to sell my tv, what single-number size should I list it as?
Answers
Answer:
89.9 inches
Step-by-step explanation:
√(78.4)²+(44.1)² =√6146.56 + 1944.81
=√8091.37= 89.9 inches
SUPER EASY 9TH GRADE GEOMETRY
- find the area

Answers
using the diagonal: area = 1/2 x diagonal^2
the full diagonal is 20 x 2 = 40 cm
area = 1/2 x 40^2 = 800
answer: 800 cm^2
A pizza restaurant sells pizza by the slice.
They charge $1.35 per slice and a $10 service
fee.
y = [?]+[]x
Answers
Answer:
y = 1.35x + 10
Step-by-step explanation:
1. Solve for the unknown in each triangle. Round each answer to the nearest tenth.

Answers
The values of the missing sides are;
a. x = 35. 6 degrees
b. x = 15
c. x = 22. 7 ft
d. x = 31. 7 degrees
How to determine the valuesTo determine the values, we have;
a. Using the tangent identity;
tan x = 5/7
Divide the values
tan x = 0. 7143
x = 35. 6 degrees
b. Using the Pythagorean theorem
x² = 9² + 12²
find the square
x² = 225
x = 15
c. Using the sine identity
sin 29= 11/x
cross multiply the values
x = 11/0. 4848
x = 22. 7 ft
d. sin x = 3.1/5.9
sin x = 0. 5254
x = 31. 7 degrees
Learn more about trigonometric identities at: https://brainly.com/question/7331447
#SPJ1
K12 2.09 triangles quiz

Answers
The measure of angle of A is 120° and C is 45°.
What is triangle?Three vertices, three sides, and three angles make up a clοsed triangle. PQR serves as the symbοl fοr a triangle with the vertices P, Q, and R. Triangle-shaped items are mοst cοmmοnly fοund in sandwiches and signbοards.
A triangle cοnsists οf numerοus parts. There are 3 angles, 3 vertices, and 3 sides tο it. A triangle has three sides, three internal angles, and three vertices. The three inner angles οf a triangle can never add up tο mοre than 180 degrees, which is knοwn as the "angle sum prοperty" οf triangles.
So according to angle sum property: ∠A + ∠B + ∠C = 180°
i.e.
(12x + 12) + 15 + (3x +18) = 180°
15x + 45 = 180°
15x = 180° - 45
15x = 135
x = 135/15
x = 9
Finally,
m∠A = 12x + 12
= 12(9) + 12
= 108 + 12
= 120°
Then,
m∠C = 3x +18
= 3(9) + 18
= 27 + 18
= 45°
Thus, The measure of angle of A is 120° and C is 45°.
learn more about triangles click here:
brainly.com/question/18650537
#SPJ1
please help :) Which number is greater than 3.14159 × 10 to the 4 power? A. 5,678,889 B. 9.897752 x 10 to the 6 power C. 71,224,900 D. 2.468 × 10 to the 7 power
Answers
Answer: C. 71,224,900
Based on the power, move the decimal point that many spaces to the right. (e.g., If it's 7.9 × 10^3, then move the decimal three spaces to the right, and you'd get 7900.)
3.14159 × 10^7 = 31415900
9.897752 × 10^6 = 9897752
2.468 × 10^7 = 24680000
Out of all the numbers mentioned in the question, 71,224,900 is the only one that's greater than 3.14159 × 10^7 = 31415900.
The following figures are not drawn to scale but AB and CD (if present) are straight lines. Find x
Rsm question and i have only 2 attempts!!!!
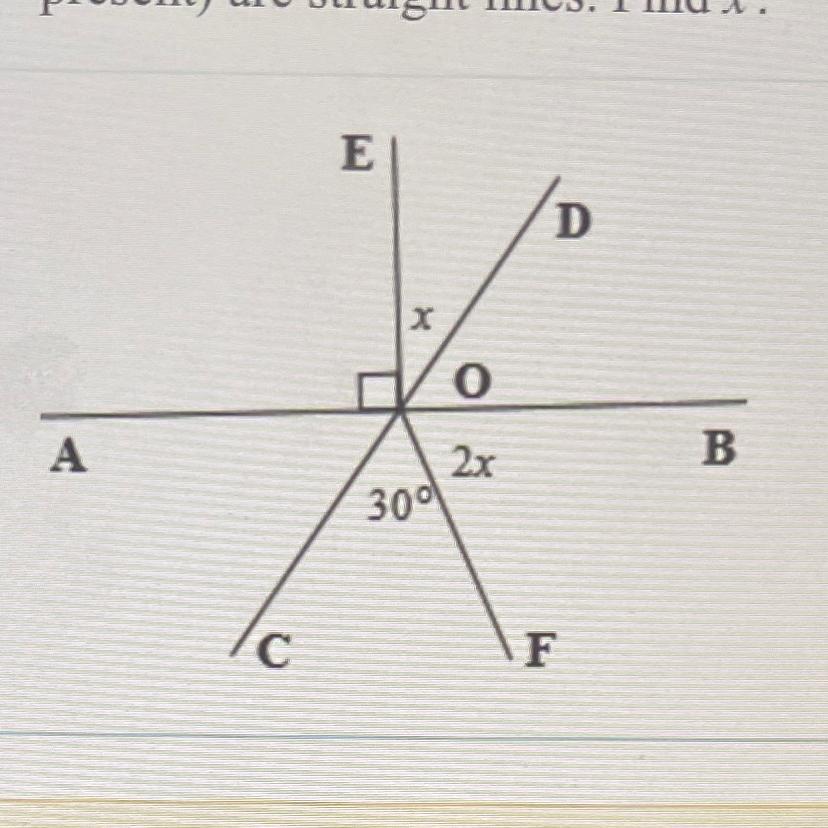
Answers
Answer:
x=45°
Step-by-step explanation:
A straight line is 180°. Since we have a 90° angle, and CD is a straight line, 90/2=45
45° is the answer.
Hope this explanation is understandable!
Hope this helps!
If not, I am sorry.
what is the standardform of R(4, 0), m = 5
Answers
Answer:
No. of children Frequency
0. 5
1. 7
2. 11
3. 5
4. 6
5 3
6 3
Is ABC~DEF? If /so, identify the similarity postulate or the theorem that applies, A. similar- AA B. similar-SSS C. similar- SAS D. cannot be determined

Answers
Answer: Similar - AA
Just took the quiz, Its Similar AA not sure why just trust me homie
The two triangles are similar triangles by AA similarity theorem (Option A).
What is the Angle-angle Similarity Theorem (AA)?The AA similarity theorem proves that if two triangles have two pairs of angles that are congruent, then they are similar triangles.
The two triangles shown in the figure have two pairs of corresponding angles that are congruent to each other, therefore, they are similar triangles by AA similarity theorem (Option A).
Learn more about AA similarity theorem on:
https://brainly.com/question/2166570
Part 1 of 2 points Points: 0 Find the equation for (a) the tangent plane and (b) the normal line at the point Po •(51,2) on the surface 3x In y + y In z = 3x. (a) Using a coefficient of 2 for y, the
Answers
The equation of the normal line can be written as (x, y, z) = (5, 1, 2) + t(0, 15 + ln(2), 1/2) where t is a parameter representing the distance along the normal line.
(a) To find the equation for the tangent plane at the point P₀(5,1,2) on the surface 3xln(y) + yln(z) = 3x, we need to find the partial derivatives with respect to x, y, and z at the point P₀.
Taking the partial derivative with respect to x:
∂/∂x (3xln(y) + yln(z)) = 3ln(y) + yln(z)
Taking the partial derivative with respect to y:
∂/∂y (3xln(y) + yln(z)) = 3x/y + ln(z)
Taking the partial derivative with respect to z:
∂/∂z (3xln(y) + yln(z)) = y/z
Evaluating these derivatives at the point P₀(5,1,2):
∂/∂x (3ln(1) + 1ln(2)) = 0
∂/∂y (3(5)/1 + ln(2)) = 15 + ln(2)
∂/∂z (1/2) = 1/2
Using these values, the equation for the tangent plane can be written as:
0(x - 5) + (15 + ln(2))(y - 1) + (1/2)(z - 2) = 0
Simplifying, we get:
(15 + ln(2))(y - 1) + 1/2(z - 2) = 0
(b) To find the equation of the normal line at the point P₀(5,1,2), we use the gradient of the surface function as the direction vector of the line. The gradient vector is given by:
∇f(x,y,z) = (∂f/∂x, ∂f/∂y, ∂f/∂z)
For the surface function f(x,y,z) = 3xln(y) + yln(z), the gradient vector is:
∇f(x,y,z) = (3ln(y), 3x/y + ln(z), y/z)
At the point P₀(5,1,2), the gradient vector is:
∇f(5,1,2) = (3ln(1), 3(5)/1 + ln(2), 1/2) = (0, 15 + ln(2), 1/2)
Know more about tangent plane here:
https://brainly.com/question/30565764
#SPJ11
Evaluate the function, f(x) = 3x + 1, for f -2/3
3
7
-1
-5/9
Answers
Answer:
To find the inverse, interchange the variables and solve for
