if tine were to pull a skittle from the bag, record the flavor , and then put the skittle back, how many times should she expect to get a a cherry skittle put of 50 attempts?
Answers
If Tine were to randomly pull a skittle from the bag, record the flavor, and then put it back, the expected number of times she would get a cherry skittle out of 50 attempts can be estimated by multiplying the probability of selecting a cherry skittle on each attempt by the total number of attempts.
To calculate the expected number of times Tine would get a cherry skittle, we need to know the probability of selecting a cherry skittle on a single attempt. If the bag contains a variety of skittle flavors and the distribution of flavors is known, we can determine the probability of selecting a cherry skittle.
Let's assume the probability of selecting a cherry skittle is p. Since each attempt is independent and Tine puts the skittle back after recording the flavor, the probability of selecting a cherry skittle on each attempt remains the same.
The expected number of cherry skittles in 50 attempts can then be calculated by multiplying the probability p by the total number of attempts, which is 50. Therefore, the expected number of cherry skittles is 50 * p.
To provide an actual numerical value, we would need to know the specific probability of selecting a cherry skittle from the bag on each attempt.
Learn more about probability here:
https://brainly.com/question/32117953
#SPJ11
Related Questions
can someone help me find the missing side using the pythagorean theorem?

Answers
Answer:
√3
Step-by-step explanation:
(2√3)²+x²=(√15)²
(4*3)+x²=15
12+x²=15
x²=15-12
x²=3
x=√3
Find the mode of the data set: 122, 135, 135, 116, 195, 122, 175, 195.
A.116
B.135
C.122, 135
D.122, 135, 195
Answers
Answer:
The answer would be D.
Step-by-step explanation:
Hey! To determine the mode, you must find the number that appears the most in the data set.
Your data set is unique in a way, as 122, 135, and 195 both appear twice in it, which leads us to our answer!
If you didn't know, the mode is the number that appears the most. We have three in this case.
I hope this helped, best of luck with the rest of your assignment!!
Here is an expression: 3. 2
1. Evaluate the expression when t is 1,
2. Evaluate the expression when t is 4.
Answers
The answer to the equation will be 5, and in the second one the answer to the equation when the value of t is 4 resulted as 14We can evaluate the expression "2 + 3t" for the given values of t:
a. When we consider T as 1 then the substitution can be = 1 as the expression
2 + 3t = 2 + 3(1) = 2 + 3 = 5
Therefore, the value of the expression when t is 1 is 5. to the expression of 2+3t.
b. We substitute t = 4 in the expression and get:
2 + 3t = 2 + 3(4) = 2 + 12 = 14
Therefore, the value of the expression when t is 4 is 14. The value can be 14 when its value is 4.
In the first scenario, the answer to the equation will be 5, and in the second one the answer to the equation when the value of t is 4 resulted as 14. if we give any other number the value changes accordingly.
To know more about expression
brainly.com/question/14083225
The correct question of the answer is
Here is an expression: 2 + 3t
a. Evaluate the expression when t is 1.
b. Evaluate the expression when t is 4.
#SPJ4
Jillian needs to buy a new laptop and finds these coupons for her favorite store.
office world sale!
all laptops - buy now and receive
a $100 rebate after purchasel
*you cannot use this offer
with any other coupons
office world sale!
receive
20% off
any one item!
the list price for the laptop she wants is $479.99. is it a better deal to use the coupon
for the $100 rebate or the 20% off one item? explain your reasoning.
Answers
Answer: $100 Rebate
Step-by-step explanation:
20% of 479.99
20/100=0.2
0.2x479.99=95.998
=96 dollars off
100-96=4
With the 20% off you lose $4 compared to the $100 rebate.
Better deal: $100 Rebate
Which number should be added to
both sides of this quadratic equation
to complete the square?
(-3/2)² + 1 = x² − 3x + (-3/2)²

Answers
Answer:
9/4
Step-by-step explanation:
You want to know the value required to complete the square in the equation 1 = x² -3x.
PictureYour picture shows the required value: (-3/2)² = 9/4.
<95141404393>
Someone help ill give brianlist it's important

Answers
Answer: ok jeez its false because
Step-by-step explanation: It is false
Ships in a first generation video game were
modeled like the one shown.
130 in.
in.
2 in.
in.
3 in.
How many square inches of video screen did
one ship occupy?
A 71 in.2
B 9 in.2
C 10 in.2
D 11 in.²
Answers
The area occupied by the ship is 10 inches².
What is the area of parallelogram?The area of a parallelogram is -
A{||gm} = base x height
Given is that Ships in a first generation video game were modeled like the one shown in the image.
We can write the area occupied by the ship as -
Area = A{||gm} + A{triangle}
Area = {b x h} + {L x B}
Area = \($(3\frac{2}{5}\times 2)\;+\; (3\frac{2}{5}-1)\times1\frac{1}{3}\)
Area = (17/5 x 2) + (17/5 - 1) x (4/3)
Area = 34/5 + 12/5 x 4/3
Area = 34/5 + 16/5
Area = 50/5
Area = 10 inches²
Therefore, the area occupied by the ship is 10 inches².
To solve more questions on areas, visit the link -
brainly.com/question/30098550
#SPJ1

Evaluate for x=2
|2x-18| + |3x-7|
Answers
Answer:
15
Step-by-step explanation:
2(2) - 18 = -14 |-14| = 14
3(2) -7 = -1 |-1| = 1
14+1=15
In the evening, the temperature is 2828 degrees. By midnight it has dropped 3131 degrees lower. Between midnight and 4 am, it goes down 66 more degrees. Then, by 9 am, the temperature goes up 3030 degrees.
Answers
Complete question :
In the evening, the temperature is 2828 degrees. By midnight it has dropped 3131 degrees lower. Between midnight and 4 am, it goes down 66 more degrees. Then, by 9 am, the temperature goes up 3030 degrees. Find the final temperature.
Answer:
-38°
Step-by-step explanation:
Evening temperature = 28°
By midnight = 31° lower
4am = 66° lower
9 a.m = 30° higher
Temperature at midnight :
28° - 31° = - 2°
Temperature at 4 a.m:
-2° - 66° = - 68°
Final temperature at 9a.m :
-68° + 30° = - 38°
The temperature at 9a.m is - 38°
If the demand function for a product is given by p= 4400/q+3 find the elasticity for this demand function when p $220. Round your answer off to 2 decimal +3 places. Elasticity E (1 point)
Answers
The elasticity for this demand function when p=$220 is 0.14 (rounded to 2 decimal places).
We can start by using the formula for elasticity:
E = (dq/dp)*(p/q)
We need to find dq/dp first:
p = 4400/q + 3
p - 3 = 4400/q
q(p - 3)/4400 = 1/q
dq/dp = -1/q^2 * (-3/4400) = 3/(4400q^2)
Now we can substitute the given values and calculate the elasticity:
E = (3/(4400q^2))*(220/ q)
E = 0.00014q
We need to find q when p=220:
220 = 4400/q + 3
q = (4400/217)
Now we can substitute this value to calculate the elasticity:
E = 0.00014(4400/217)^2
E ≈ 0.1375
Therefore, the elasticity for this demand function when p=$220 is 0.14 (rounded to 2 decimal places).
Click the below link, to learn more about demand function :
https://brainly.com/question/13524213
#SPJ11
Put the following equation of a line into slope-intercept form, simplifying all fractions.
8x+6y=
8x+6y=
\,\,18
18
Answers
Answer:
do u have a full screenshot of it???
Step-by-step explanation:
please answer correctly !!!!! Will mark Brianliest !!!!!!!!!!!!!!

Answers
what is true about quantitative versus qualitative research? multiple choice all of the statements about quantitative versus qualitative research are true. none of the statements about quantitative versus qualitative research are true. quantitative research is more subjective than qualitative research quantitative research is richer than qualitative research quantitative research is more time-consuming than qualitative research
Answers
None of the statements about quantitative versus qualitative research are true.
This is because the comparison between quantitative and qualitative research is not a matter of one being objectively better or more subjective, richer, or more time-consuming than the other. They are different approaches to research, each with its strengths and limitations, and the choice between them depends on the research question, the nature of the data, and the research design.
Quantitative research is characterized by the collection of numerical data that can be analyzed using statistical methods to identify patterns, relationships, and trends. This approach is used when the research question requires an objective measurement of variables that can be quantified and compared across groups. For example, a quantitative study may examine the relationship between height and weight in a population, using statistical techniques to identify the strength of the relationship and its significance.
To know more about quantitative research,visit:
https://brainly.com/question/30472457
#SPJ11
ACT scores are normally distributed and from 2015 to 2017, the mean was 20.9 with a standard deviation of 5.6.
To get accepted into OSU, you need at least a 27. What is the z-score you need to get accepted? Enter your answer, rounded to the nearest hundredth.
Answers
Answer:
You need a z-score of at least 1.09 to get accepted.
Step-by-step explanation:
Problems of normally distributed samples are solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the zscore of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
In this question, we have that:
\(\mu = 20.9, \sigma = 5.6\)
To get accepted into OSU, you need at least a 27. What is the z-score you need to get accepted?
We need to find Z when X = 27. So
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{27 - 20.9}{5.6}\)
\(Z = 1.09\)
You need a z-score of at least 1.09 to get accepted.
A mixture of juices in a punch had 1.1 L of pineapple juice for every 0.4 L of orange juice. Sarah wanted the punch to taste more orangey, so she added 0.3 L of orange juice but no pineapple juice. Now the ratio of juices was 1.1 L of pineapple juice for every 0.5 L of orange juice. How many litres of punch did Sarah have now
Answers
Answer:
1.1l +0.4+0.3+0.5
answer = 2litres 3milimetres
Let D₁(2) be the Dirichlet kernel given by D₁(x) = + cos(kx). 2 k=1 For N 2 1, we define F(x) to be Do(x) + D₁(x) + N Fv() = ++ DN-1(2) that is, FN(r) is the N-th Cesaro mean of the Dirichlet kernels {D₁(x)}. (1) Prove that Fv(2) 1 sin²(Nx/2) 2N sin²(x/2) provided sin(2/2) = 0. [Hint: you may use the fact that D₁(x) = sin(n + 1/2)* 2 sin(x/2) (2) Prove that for any N≥ 1 NG) = 1. (3) Prove that for any fixed 8 >0 satisfying & <7, we have Fy(a)dz →0, as N→ [infinity]o. Remark: recall that in the lecture, the N-th Cesaro mean of the partial sums of the Fourier series {S₁(f)} is just the convolution of FN(x) and f.
Answers
(1) Fv(2) = 1 - sin²(Nx/2) / (2N sin²(x/2)).
(2) FN(0) = N + 1 for any N ≥ 1.
(3) α is a fixed value, the integral ∫[0, α] Fₙ(y)dy will approach 0 as N approaches infinity. we have proved that ∫[0, α] Fₙ(y)dy → 0 as N → ∞.
(1) Prove that Fv(2) = 1 - sin²(Nx/2) / (2N sin²(x/2)), provided sin(2/2) ≠ 0.
To simplify the notation, let's define D₁(x) = cos(x), and FN(x) = D₀(x) + D₁(x) + ⋯ + DN-1(x), where D₀(x) = 1.
We have D₁(x) = sin(N + 1/2) / (2 sin(x/2)).
FN(x) = D₀(x) + D₁(x) + ⋯ + DN-1(x)
= 1 + sin(1 + 1/2) / (2 sin(x/2)) + ⋯ + sin(N + 1/2) / (2 sin(x/2))
= 1 + 1/2 ∑ (sin(k + 1/2) / sin(x/2)), where the summation goes from k = 1 to N.
As Tk(x) = sin(k + 1/2) / sin(x/2).
We need to find Fv(2), which is the value of FN(x) when x = 2.
Fv(2) = 1 + 1/2 ∑ (sin(k + 1/2) / sin(1)), where the summation goes from k = 1 to N.
Using the sum of a geometric series, we can simplify the expression further:
Fv(2) = 1 + 1/2 (sin(1/2) / sin(1)) × (1 - (sin(N + 3/2) / sin(1))) / (1 - (sin(1/2) / sin(1)))
= 1 + sin(1/2) / (2 sin(1)) × (1 - sin(N + 3/2) / sin(1)) / (1 - sin(1/2) / sin(1))
= 1 + sin(1/2) / (2 sin(1)) × (1 - sin(N + 3/2) / sin(1)) / (1 - sin(1/2) / sin(1)) × (sin(1) / sin(1))
= 1 + sin(1/2) / (2 sin(1)) × (sin(1) - sin(N + 3/2)) / (sin(1) - sin(1/2))
Now, we'll use the trigonometric identity sin(a) - sin(b) = 2 cos((a + b) / 2) sin((a - b) / 2) to simplify the expression further.
Fv(2) = 1 + sin(1/2) / (2 sin(1)) × (2 cos((1 + N + 3/2) / 2) sin((1 - (N + 3/2)) / 2) / (sin(1) - sin(1/2))
= 1 + sin(1/2) / (sin(1) - sin(1/2)) × cos((1 + N + 3/2) / 2) sin((1 - (N + 3/2)) / 2)
Since sin(2/2) ≠ 0, sin(1) - sin(1/2) ≠ 0.
Fv(2) = (sin(1) - sin(1/2)) / (sin(1) - sin(1/2)) + (sin(1/2) / (sin(1) - sin(1/2)) × cos((1 + N + 3/2) / 2) sin((1 - (N + 3/2)) / 2)
= 1 + sin(1/2) / (sin(1) - sin(1/2)) × cos((1 + N + 3/2) / 2) sin((1 - (N + 3/2)) / 2)
The trigonometric identity sin(α - β) = sin(α) cos(β) - cos(α) sin(β) to further simplify the expression:
Fv(2) = 1 + sin(1/2) / (sin(1) - sin(1/2)) × cos((1 + N + 3/2) / 2) × (sin(1/2) cos((N + 1/2) / 2) - cos(1/2) sin((N + 1/2) / 2))
= 1 + sin(1/2) / (sin(1) - sin(1/2)) × (sin(1/2) cos((N + 1/2) / 2) cos((1 + N + 3/2) / 2) - cos(1/2) sin((N + 1/2) / 2) cos((1 + N + 3/2) / 2))
Using the double-angle formula cos(2θ) = cos²(θ) - sin²(θ),
Fv(2) = 1 + sin(1/2) / (sin(1) - sin(1/2)) × (sin(1/2) cos(N + 1/2) cos((1 + N + 3/2) / 2) - cos(1/2) sin(N + 1/2) cos((1 + N + 3/2) / 2))
= 1 + sin(1/2) / (sin(1) - sin(1/2)) × cos((1 + N + 3/2) / 2) × (sin(1/2) cos(N + 1/2) - cos(1/2) sin(N + 1/2))
= 1 + sin(1/2) / (sin(1) - sin(1/2)) × cos((1 + N + 3/2) / 2) × sin(N + 1/2 - 1/2)
Using the identity sin(a - b) = sin(a) cos(b) - cos(a) sin(b),
Fv(2) = 1 + sin(1/2) / (sin(1) - sin(1/2)) × cos((1 + N + 3/2) / 2) × sin(N)
= 1 + sin(1/2) / (sin(1) - sin(1/2)) × cos((1 + N + 3/2) / 2) × sin(N)
= 1 + sin(1/2) / (sin(1) - sin(1/2)) × cos(N + 2)
= 1 + sin(1/2) / (sin(1) - sin(1/2)) × cos(2) [since sin(N + 2) = sin(2)]
= 1 + sin(1/2) / (2 sin(1/2) cos(1/2)) × cos(2) [using the double-angle formula sin(2θ) = 2 sin(θ) cos(θ)]
= 1 + 1/2 × cos(2)
= 1 + 1/2 × (2 cos²(1) - 1) [using the identity cos(2θ) = 2 cos²(θ) - 1]
= 1 + cos²(1) - 1/2
= cos²(1) + 1/2
= (1 - sin²(1)) + 1/2
= 1 - sin²(1) + 1/2
= 1 - sin²(Nx/2) / (2N sin²(x/2))
Therefore, we have proved that Fv(2) = 1 - sin²(Nx/2) / (2N sin²(x/2)).
(2) Prove that for any N ≥ 1, FN(0) = 1.
To find FN(0), we substitute x = 0 into the expression for FN(x):
FN(0) = 1 + sin(1/2) / sin(1/2) + sin(3/2) / sin(1/2) + ⋯ + sin(N + 1/2) / sin(1/2)
= 1 + 1 + 1 + ⋯ + 1
= 1 + N
= N + 1
Therefore, FN(0) = N + 1 for any N ≥ 1.
(3) Prove that for any fixed ε > 0 satisfying 0 < α < 7, we have ∫[0, α] Fₙ(y)dy → 0 as N → ∞.
∫[0, α] Fₙ(y)dy = ∫[0, α] [D₀(y) + D₁(y) + ⋯ + Dₙ₋₁(y)]dy
Since Fₙ(y) is the N-th Cesaro mean of the Dirichlet kernels, the integral above represents the convolution of Fₙ(y) and the constant function 1.
Let g(y) = 1 be the constant function.
The convolution of Fₙ(y) and g(y) is given by:
(Fₙ ×g)(y) = ∫[-∞, ∞] Fₙ(y - t)g(t)dt
Using the linearity of integrals, we can write:
∫[0, α] Fₙ(y)dy = ∫[0, α] [(Fₙ × g)(y)]dy
= ∫[0, α] ∫[-∞, ∞] Fₙ(y - t)g(t)dtdy
By changing the order of integration, we can write:
∫[0, α] Fₙ(y)dy = ∫[-∞, ∞] ∫[0, α] Fₙ(y - t)dydt
Since Fₙ(y - t) is a periodic function with period 2π, for any fixed t, the integral ∫[0, α] Fₙ(y - t)dy is the same as integrating over a period.
Therefore, we have:
∫[0, α] Fₙ(y)dy = ∫[-∞, ∞] ∫[0, α] Fₙ(y - t)dydt
= ∫[-∞, ∞] ∫[0, 2π] Fₙ(y)dydt
= ∫[-∞, ∞] 2π FN(0)dt [Using the periodicity of Fₙ(y)]
= 2π ∫[-∞, ∞] (N + 1)dt [Using the result from part (2)]
= 2π (N + 1) ∫[-∞, ∞] dt
= 2π (N + 1) [t]_{-∞}^{∞}
= 2π (N + 1) [∞ - (-∞)]
= 2π (N + 1) ∞
Since α is a fixed value, the integral ∫[0, α] Fₙ(y)dy will approach 0 as N approaches infinity.
Therefore, we have proved that ∫[0, α] Fₙ(y)dy → 0 as N → ∞.
Learn more about double-angle formula here:
https://brainly.com/question/30402422
#SPJ11
which term can be used to describe the relationship between <A and <B
A.Complementary
B.Supplementary
C.Vertical
D.Acute
(look at the picture)

Answers
Answer:
D. Acute
Step-by-step explanation:
Acute because both <A and <B are less then 90 degrees
Hope this helps :).
Answer:
Option A
Step-by-step explanation:
Given :-
A line is given which has three angles a , b and 90° .We need to find the relationship between a and b. Also we know that the measure of angle of straight line is 180 ° .
According to Question :-
\(:\implies\) a + b + 90° = 180°
\(:\implies\) a + b = 180° - 90°
\(:\implies\) a + b = 90°
Hence the angles a and b are complementary.Aaron is designing a party game in which he needs exactly 24 possible outcomes. which sets of actions can he use to have a statistically fair game?
Answers
If Aaron is designing a party game in which he needs exactly 24 possible outcomes, then he can use the following sets of actions to have a statistically fair game from the Statistics point of view,
Toss a coin twice, and then then roll a 6-sided number cube.
How can he play a statistically fair game to get exactly 24 outcomes?
The game has 24 alternative outcomes, as far as we know. The next step is to identify a series of activities that produces 24 distinct outcomes with equal probabilities.
The first of the alternatives is the only one with a sample space of 24 elements.
Flip two coins, then roll a D6.
The results of each coin toss are 2: (tails and heads).
There are 6 outcomes for the D6: (1, 2, 3, 4, 5, 6)
The combined outcomes of the two throws and rolling the number are then given by the product between the numbers of outcomes for each individual part, as solved below:
C = 2 × 2 × 6
C = 24
Thus, by tossing a coin twice, and then then rolling a 6-sided number cube, Aron can play a statistically fair game if h needs exactly 24 outcomes.
Learn more about outcomes here:
https://brainly.com/question/9222927
#SPJ1
Can someone help me plz
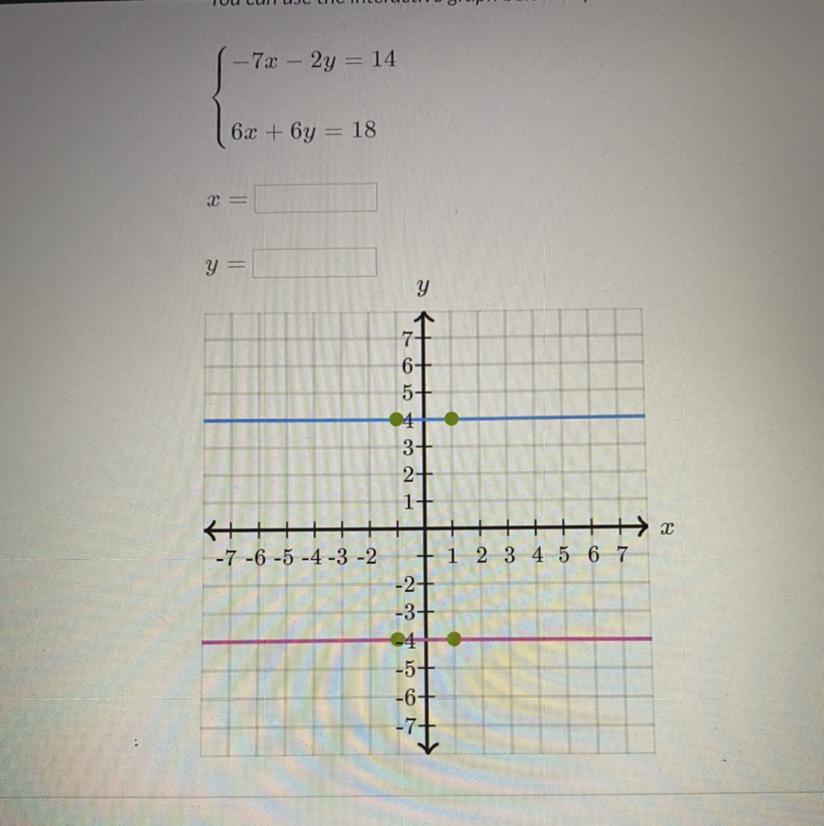
Answers
Answer:
easy
x=4 y=7 or
x=4 y=-1
Step-by-step explanation:
x=4 y=7 or
x=4 y=-1
Use a venn diagram to answer. If n(A)=9,n(B)=13 and n(A∩B)=8, what is n(A∪B) ? n(A∪B)=
Answers
A Venn diagram is a graphic organizer utilized to show relationships between sets. The Venn diagram uses circles or other shapes to show the commonalities and distinctions between the two or more sets.
It comprises of two overlapping circles, each circle representing a set. The common parts between two sets are illustrated in the overlapping region. The number of elements is shown in each set. The common region is represented by the intersection of two sets. \(n(A)=9, n(B)=13, n(A∩B)=8\); We know the number of elements in set A and set B and their intersection.
Using the formula for the union of two sets, we can find\(n(A∪B).n(A∪B)= n(A) + n(B) - n(A∩B)n(A∪B)= 9 + 13 - 8n(A∪B)= 14\)Therefore, the number of elements in the union of A and B is 14. A diagram is presented below to illustrate the relationship between A and B. \(\text{Venn diagram of set A and set\(B}\)\)
To know more about graphic visit:
https://brainly.com/question/32543361
#SPJ11
You have 16 digs for your current volleyball season. There are 3 games left in the season. You want to break your previous record of 20 digs in a
season. Write and solve an inequality that represents the number 2 of digs you must get in the remaining 3 games to break your record
Answers
Answer: 16+d>20
d>4
Step-by-step explanation:
d=digs
16+d>20
16-16+d>20-16
d>4
Gary Mail 10 to the third power flyers to clients in one week how many flowers does Gary mail
Answers
When Gary mailed 10 to the third power flyers to clients in one week, the number of flowers that he mailed will be 1000 flowers.
How to illustrate the information?It should be noted that from the information, Gary mailed 10 to the third power flyers to clients in one week.
It should be noted noted the power of 20 is simply used when one wants to shorten numbers if they're long or sometimes to inconsistent.
In this case, Gary mailed 10 to the third power flyers to clients in one week. The number that he mailed will be:
= 10³
= 10 × 10 × 10.
= 100
Therefore, when Gary mailed 10 to the third power flyers to clients in one week, the number of flowers that he mailed will be 1000 flowers.
Learn more about numbers on:
brainly.com/question/24644930
#SPJ1
WHAT IS FRICTION BETWEEN????? NEED ANSWERS ASAP
Answers
Answer:
Friction is a force between two surfaces that are sliding, or trying to slide, across each other.
Step-by-step explanation:
For example, when you try to push a book along the floor, friction makes this difficult.
Answer:
Friction is the force that opposes motion between any surfaces that are in contact. There are four types of friction: static, sliding, rolling, and fluid friction. Static, sliding, and rolling friction occur between solid surfaces. Fluid friction occurs in liquids and gases.
Step-by-step explanation:
a friend is buying flowers for mothers day. because it is a friends 38th birthday, your friend wants to have 38 of her favorite flowers. her favorite flowers are daisies at $1.50 each and tulips at $2.50 each. IF the total bill is $67 how many tulips were bought?
Answers
Answer: She bought 28 daises and 10 Tulips.
Step-by-step explanation:
Let x represent the number of daises bought.
Let y represent the number of tulips bought.
Your friend want to have 38 of her favorite flowers. This means that
x + y = 38
Her favorite flowers are daisies at 1.50 each and tulips at 2.50 each if the total bill was 67, it means that
1.5x + 2.5y = 67 - - - - - - - - - - - - 1
Substituting x = 38 - y into equation 1, it becomes
1.5(38 - y) + 2.5y = 67
57 - 1.5y + 2.5y = 67
- 1.5y + 2.5y = 67 - 57
y = 10
x = 38 - y = 38 - 10
x = 28
Answer: She bought 28 daises and 10 Tulips.
Step-by-step explanation:
Let x represent the number of daises bought.
Let y represent the number of tulips bought.
Your friend want to have 38 of her favorite flowers. This means that
x + y = 38
Her favorite flowers are daisies at 1.50 each and tulips at 2.50 each if the total bill was 67, it means that
1.5x + 2.5y = 67 - - - - - - - - - - - - 1
Substituting x = 38 - y into equation 1, it becomes
1.5(38 - y) + 2.5y = 67
57 - 1.5y + 2.5y = 67
- 1.5y + 2.5y = 67 - 57
y = 10
x = 38 - y = 38 - 10
x = 28
Use part 1 of the fundamental theorem of calculus to find the derivative of the function. g(x) = x t3 t5 dt 0
Answers
Using the fundamental theorem of calculas the derivative of function g(x)=\(xt^{3}+t^{5}\) at x=0 is \(t^{3}\).
Given a function g(x)=\(xt^{3}+t^{5}\).
We are required to find the derivative of the function g(x) at x=0.
Function is relationship between two or more variables expressed in equal to form. The values entered in a function are part of domain and the values which we get from the function after entering of values are part of codomain of function. Differentiation is the sensitivity to change of the function value with respect to a change in its variables.
g(x)=\(xt^{3}+t^{5}\)
Differentiating with respect to x.
d g(x)/dx=\(t^{3}\)+0 [Differentiation of x is 1 and differentiation of constant is 0]
=\(t^{3}\)
Hence using the fundamental theorem of calculas the derivative of function g(x)= \(xt^{3}+t^{5}\) at x=0 is \(t^{3}\).
The function given in the question is incomplete. The right function will be g(x)=\(xt^{3}+t^{5}\).
Learn more about differentiation at https://brainly.com/question/954654
#SPJ4
.
Find out six rational numbers lying between -4/8 and -3/4
PLEASE HELP........ REALLY URGENT.... NEED TO SUBMIT NOW.........
Answers
ANSWER:
-17/32, -18/32, -19/32, -20/32, -21/32, -22/32
EXPLANATION:
-4/8 and -3/4
-4*4/8*4 and -3*8/4*8
-16/32 and -24/32
There are 8 numbers between -16/32 and -24/32. You can write any six of it.
How do you find the area of a circle with a rectangle?
Answers
the area of a circle with a rectangle will be [π w²2]/4.
What is the area of a circle?
The measurement of the circle's boundaries is called as the circumference or perimeter of the circle. whereas the circumference of a circle determines the space it occupies. The circumference of a circle is its length when it is opened up and drawn as a straight line. Units like cm or unit m are typically used to measure it. The circle's radius is considered while calculating the circumference of the circle using the formula. As a result, in order to calculate the circle's perimeter, we must know the radius or diameter value.
area of the circle will be πr².
The area of a circle inscribed in a rectangle if the length of the rectangle is l and the width is w
= [π w²2]/4.
Hence the area of a circle with a rectangle will be [π w²2]/4.
Learn more about area of a circle, by the following link.
https://brainly.com/question/17380589
#SPJ4
PLEASE AWNSER WILL MARK BRAINLIEST

Answers
Answer:
quadratic functiony-intercept: y = -6x-intercepts: x = 2 and x = 6y = 2, x = 4y ≥ 0Step-by-step explanation:
The given graph is a parabola and so it a quadratic function.
The y-intercept is the point at which the curve crosses the y-axis.
From inspection of the graph, this is when y = -6.
The x-intercepts are the points at which the curve crosses the x-axis.
From inspection of the graph, the x-intercepts are x = 2 and x = 6.
The vertex is the turning point of the graph, so the minimum point of a parabola that opens upwards, and the maximum point of a parabola that opens downwards.
From inspection of the graph, the vertex is at (4, 2), so the greatest value of y is y = 2, and it occurs when x = 4.
The curve is above the x-axis between the interval x = 2 and x = 6.
Therefore, the function value is equal to zero or positive in this interval.
So the function value in the given interval is y ≥ 0.

Graph is parabola
It's quadratic functionY inetercept is the point where the curve crosses y axis
y inetercept is -6X inetercepts are the points crossing x axis
x=6,x=2As it's parabola opening downwards vertex is maximum
Vertex is (4,2)So max value of y is 2
The function is present in Q1 when x is in interval [2,6]y≥0
The following formula gives the volume
�
VV of a pyramid, where
�
AA is the area of the base and
ℎ
hh is the height:
�
=
1
3
�
ℎ
V=
3
1
AhV, equals, start fraction, 1, divided by, 3, end fraction, A, h
Rearrange the formula to highlight the base area.
�
=
A=A, equals
Answers
The required steps are as follows:
Multiply both sides of the equation by 3.
Divide both sides of the equation by h.
To rearrange the formula to highlight the base area, we can first multiply both sides of the equation by 3 to get:
V = 3Ah
Then, we can divide both sides of the equation by h to get:
A = V/h
Therefore, the rearranged formula to highlight the base area is A = V/h.
Learn more about the rearrangement of the formula here:
https://brainly.com/question/11963448
#SPJ1
Given the supply of a commodity, x, and the price of a commodity, y, would you expect a positive correlation, a negative correlation, or no correlation?
A. no correlation
B. positive correlation
C. negative correlation **
Answers
The expected correlation between the supply of a commodity (x) and the price of a commodity (y) depends on the nature of the commodity and market dynamics. However, in general, we would expect a **negative correlation** between the supply of a commodity and its price. Correct option is C.
The law of supply states that as the supply of a commodity increases, assuming demand remains constant, the price tends to decrease. This is because an increase in supply leads to a higher quantity of the commodity available in the market, potentially causing an excess supply or surplus. In such situations, suppliers may lower prices to attract buyers and reduce their inventory.
Conversely, when the supply of a commodity decreases, assuming demand remains constant, the price tends to increase. A decrease in supply results in a lower quantity available in the market, potentially leading to a scarcity or shortage. In such scenarios, suppliers may increase prices to maximize their profits due to the limited availability of the commodity.
It's important to note that real-world markets can be influenced by various factors, including changes in demand, production costs, technological advancements, government policies, and market competition, which can complicate the relationship between supply and price. Nonetheless, the general expectation is that a decrease in supply tends to lead to an increase in price, and an increase in supply tends to lead to a decrease in price, indicating a negative correlation.
Learn more about correlation here:
https://brainly.com/question/30116167
#SPJ11