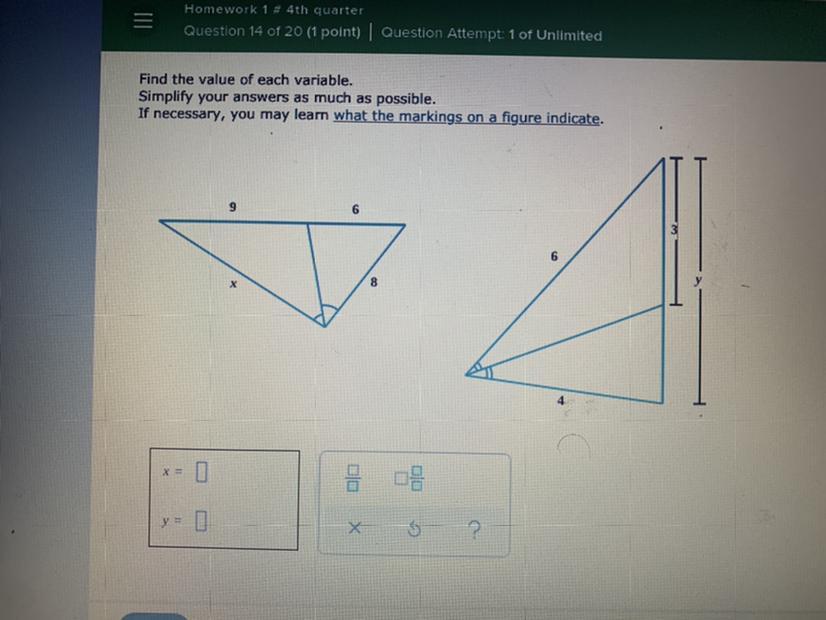
Answers
Here, we have two pairs of similar triangles.
Let's find the values of x and y.
• Sol,vin,g for x:
Given:
Length of longer base = 9
Length of shorter base = 5
Length of smaller leg = 8
Let's solve for x.
Since the triangles are similar, the corresponding sides will be in proportion.
To solve for x, apply the proportionality equation:
\(\frac{9}{x}=\frac{6}{8}\)Cross multiply and solve for x:
\(\begin{gathered} 6x=9*8 \\ \\ 6x=72 \\ \\ \text{ Divide both sides by 6:} \\ \frac{6x}{6}=\frac{72}{6} \\ \\ x=12 \end{gathered}\)• Solving for y:
Given:
Length of longer base = 3
Length of longer leg = 6
Length of smaller leg = 4
Length of total base = y
To solve for y, we have the equation:
\(\frac{6}{3}=\frac{4}{y-3}\)Cross multiply and solve for y:
\(\begin{gathered} 6(y-3)=4*3 \\ \\ 6y-6(3)=12 \\ \\ 6y-18=12 \\ \\ \text{ Add 18 to both sides:} \\ 6y-18+18=12+18 \\ \\ 6y=30 \\ \\ \text{ Divide both sides by 6:} \\ \frac{6y}{6}=\frac{30}{6} \\ \\ y=5 \end{gathered}\)ANSWER:
• x = 12
• y = 5
Related Questions
What is the area in square centimeters of the trapezoid below

Answers
Answer:
area = 1/2(a+b)h
a= 8.2 cm
b= 22.9 cm.
h= 9.8
therefore area = 77.91 sqcm
The area in square centimeters of the trapezoid below is 77.91 .
How to find the area of a trapezoid?The area of a trapezoid is the half of the product of sum of its parallel sides to the height of that trapezoid (the distance between those parallel sides).
Thus, if we have Length of its parallel sides = 'a' and 'b' units respectively
Perpendicular distance between its parallel sides = 'h' units,
Area = 1/2(a+b)h
a= 8.2 cm
b= 22.9 cm.
h= 9.8
Area = 1/2(8.2 + 22.9)9.8
therefore, area = 77.91 sqcm
Learn more about the area;
https://brainly.com/question/1658516
#SPJ2
If EF = 6 and EG=21 find the value of FG. The drawing is not to scale

Answers
Indi, Mark, and Tess each pick a slip of paper with a subtraction
expression written on it. The person holding the card with the
greatest value wins a prize. Who wins the prize?
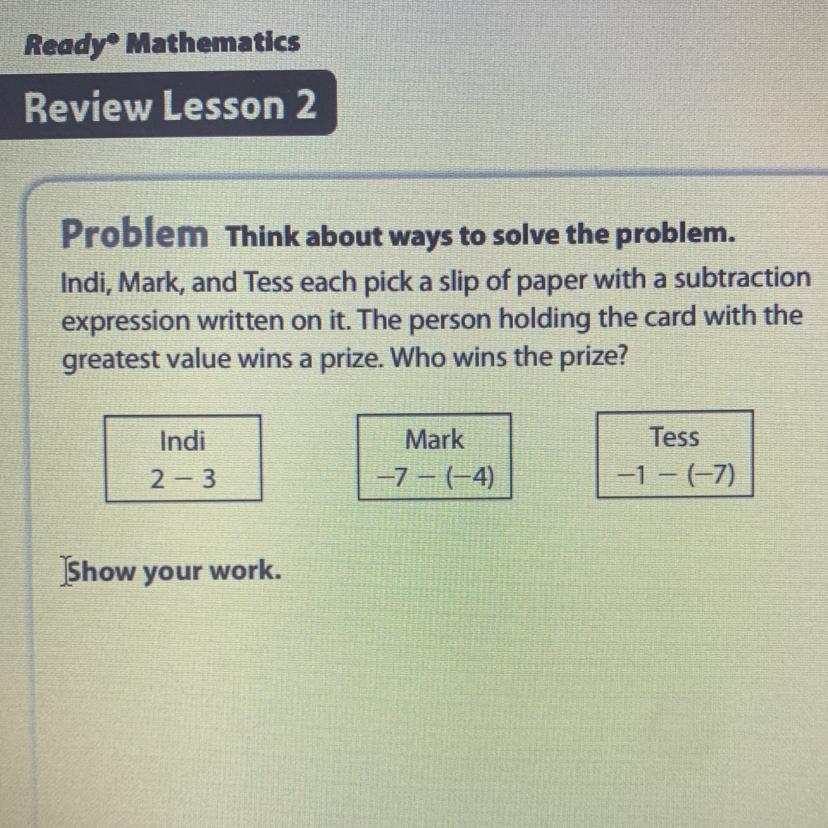
Answers
Answer:
Tess wins the prize.
Step-by-step explanation:
\(\boxed{\text{Indi}: 2-3}\)
\(\boxed{\text{Mark}: -7-(-4)}\)
\(\boxed{\text{Tess}: -1-(-7)}\)
The expression of Indi's card is 2 - 3 = -1
The expression of Mark's card is -7 - (-4) = -7+4= -3
The expression of Tess's card is -1 - (-7) = -1+7= 6
What is the value of the expression below
x = 8 and y = 3
9x + 7y
Answers
9x+7y
x=8 and y=3
9(8)+7(3)
72+7(3)
72+21
=93
You throw a fair die n times. Denote by Pn the probability of throwing an even number of sixes in n throws.(a) Prove the following difference equation 5 Pn 1 (- 1 – Pn-1) + pn-1. 6Pn(b) Solve above difference equation to obtain an explicit formula for Pn.
Answers
(a) Pₙ = (1/6) * (1 - Pₙ₋₁) + (5/6) * Pₙ₋₁
This is the difference equation that we needed to prove.
(b) The difference equation and obtain an explicit formula for Pn,
Pₙ = (1 + 4Pₙ₋₁) / 6
What is the equivalent expression?Expressions that are equivalent serve the same purpose regardless of appearance. When we employ the same variable value, two algebraic expressions that are equivalent have the same value.
To prove the given difference equation for Pₙ , let's break it down into two parts: the case where the nth throw results in a six and the case where it does not.
(a) Case: The nth throw results in a six
In this case, we need to consider the previous (n-1) throws to determine the probability of having an even number of sixes. Since the (n-1)th throw cannot be a six, the probability of having an even number of sixes in (n-1) throws is Pₙ₋₁.
Now, for the nth throw to be a six, we have a probability of 1/6. Therefore, the probability of having an even number of sixes in n throws, given that the nth throw is a six, is (1/6) * (1 - Pₙ₋₁).
This is because (1 - Pₙ₋₁) represents the probability of having an odd number of sixes in (n-1) throws.
(b) Case: The nth throw does not result in a six
In this case, we still need to consider the previous (n-1) throws to determine the probability of having an even number of sixes.
Since the nth throw does not result in a six, the probability of having an even number of sixes in (n-1) throws remains the same, which is Pₙ₋₁.
Now, for the nth throw to not result in a six, we have a probability of 5/6. Therefore, the probability of having an even number of sixes in n throws, given that the nth throw does not result in a six, is (5/6) * Pₙ₋₁.
Combining the probabilities from both cases, we get:
Pₙ = (1/6) * (1 - Pₙ₋₁) + (5/6) * Pₙ₋₁
This is the difference equation that we needed to prove.
To solve the difference equation and obtain an explicit formula for Pn, we can rearrange the equation:
6Pₙ = 1 - Pₙ₋₁ + 5Pₙ₋₁
6Pₙ = 1 + 4Pₙ₋₁
Pₙ = (1 + 4Pₙ₋₁) / 6
Now, we can use this recursive formula to find explicit values for Pₙ. We start with P₀, which represents the probability of having an even number of sixes in 0 throws (which is 1):
P₀ = 1
Then, we can use the recursive formula to calculate P₁, P₂, P₃, and so on, until we reach the desired value of Pₙ.
Hence,
(a) Pₙ = (1/6) * (1 - Pₙ₋₁) + (5/6) * Pₙ₋₁
This is the difference equation that we needed to prove.
(b) the difference equation and obtain an explicit formula for Pn,
Pₙ = (1 + 4Pₙ₋₁) / 6
To learn more about the equivalent expression visit:
https://brainly.com/question/2972832
#SPJ4
A boy who is flying a kite lets out 300 feet of string which makes an angle of 60o with the ground. Assuming that the string is stretched taut, find, to the nearest foot, how high the kite is above ground.
Answers
See the attachment for better understanding.
Given : Length of string (AC) = 300ft
To Find : Height of the kite from ground (AB)
\(:\implies\sf\:sin60^{\circ}=\dfrac{AB}{AC}\)
\(:\implies\sf\:\dfrac{\sqrt{3}}{2}=\dfrac{H}{300}\)
\(:\implies\sf\:H=\dfrac{300\sqrt{3}}{2}\)
\(:\implies\sf\:H=150\sqrt{3}\)
\(:\implies\:\boxed{\bf{\red{H\approx 260\:feet}}}\)
Hope it helps !

The kite is 260 ft. above ground.
What is right triangle?"It is a triangle whose one of the angle is 90"
What is sine of the angle?For right triangle the sine of the angle 'x' is,
sin(x) = opposite side of angle x / hypotenuse
For given example,
Consider the diagram given below.
KL represents the string length.
So, KL = 300 ft.
A string makes an angle of 60° with the ground.
This means, ∠KLM = 60°
Let, 'h' represents the height of of the kite above the ground.
For a right triangle KLM,
⇒ sin(KLM) = KM/KL
⇒ sin(60°) = h/300
⇒ h = sin(60°) × 300
⇒ h = 259.8 ft.
⇒ h ≈ 260 ft.
Therefore, the kite is 260 ft. above ground.
https://brainly.com/question/16853308
Learn more about sine here:
#SPJ2

help me with algebra please
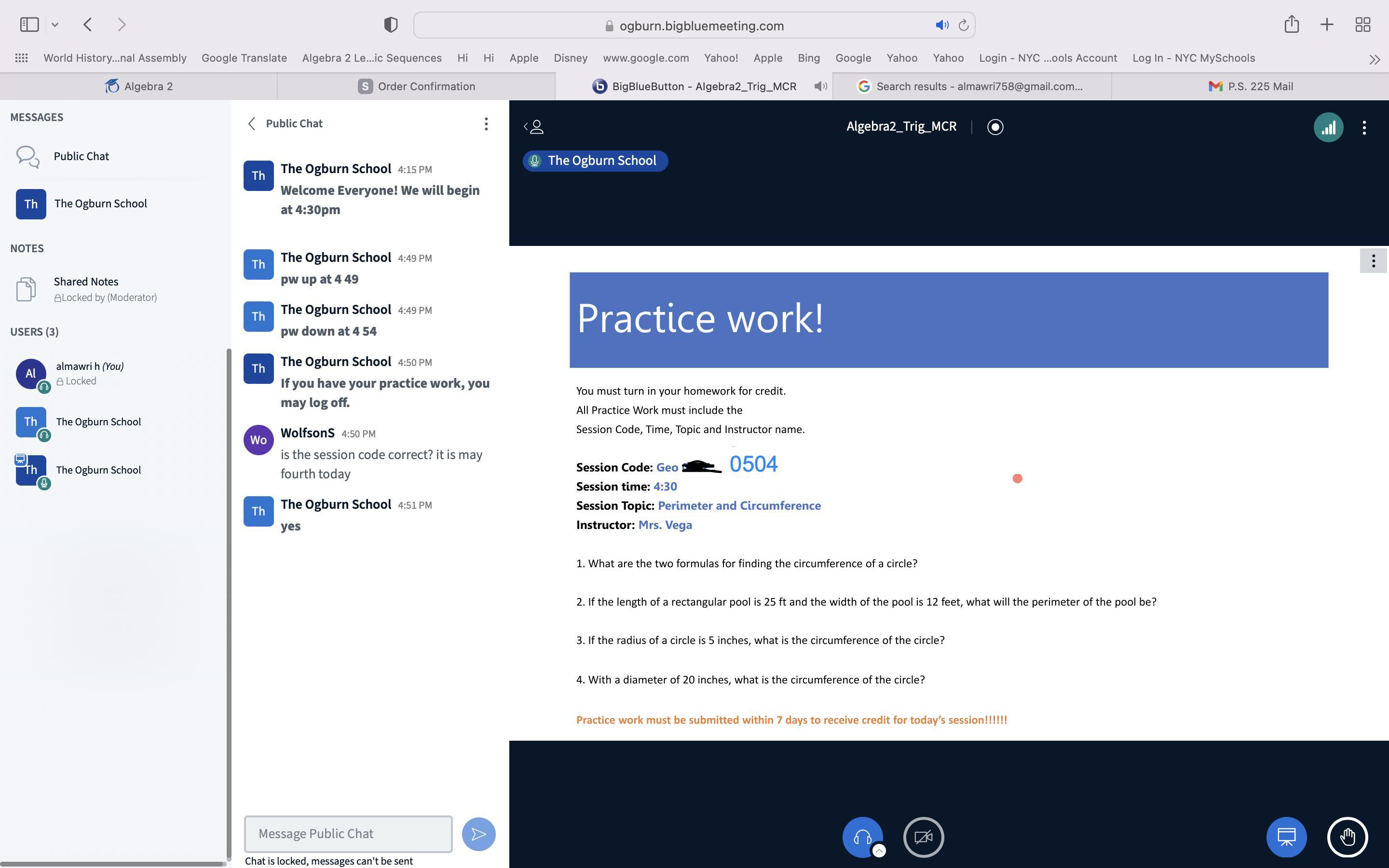
Answers
Answer:
1. Circumference of a circle = 2πr or πd (r=radius and d=diameter)
2. Perimeter = 74 feet
3. 2π*5 = 10π
4. π*20 = 20π
Step-by-step explanation:
1. Diameter is equal to radius*2.
2. 25+25+12+12=74
3. Substitute 5 for r in the formula.
4. Substitute 20 for d in the second formula.
A bowl of fruit contains 10 oranges, 12 apples, 6 plums, and 2 peaches. If you want to compare the number of apples to oranges what is the correct way to express this numerically and what language correctly describes the comparison?
Answers
Answer:
Kindly check explanation
Step-by-step explanation:
To compare the number of apples to oranges
Number of apples = 12
Number of oranges = 10
Number of apples in terms of oranges :
12 /10 = 1.2
Number of apples = 1.2(number of oranges)
If number of apples = x
Number of oranges = y
x = 1.2y
There are 1.2 times the number of apples than number of oranges.
The water level f, in feet, at a certain beach is modeled by the function
\(f(t)=2sin(2\pi t)/24\), where is the number of hours since the level was measured.
What is the amplitude of the function? What does it mean in this context?
What is the period of the function? What does it mean in this context?
Sketch a graph of the function over 72 hours.
![The water level f, in feet, at a certain beach is modeled by the function [tex]f(t)=2sin(2\pi t)/24[/tex],](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/xfhe6K6ZCS6WcXpEUc3YlOkDyp0qm31V.jpeg)
Answers
Answer:
1. Amplitude = 2 feet (max height level of water on the beach)
2. Periodicity = 24 hours (water level reaches 2 ft max every 24 hours or 0 feet minimum every 24 hours
3. Graph attached with explanation
Step-by-step explanation:
For a sine function, sin(x), the maximum value is 1 when x is π/2, 5π/2, 9π/2...
The minimum value is -1 at x = 0, π, 3π/2, 2π,...
a sin(x) will have the maximum value(amplitude) of |a · 1| = |a|
The given function is
\(f(t) = 2 \sin\left(\dfrac{2\pi t}{24}\right)\\\\\dfrac{2\pi t}{24} = \dfrac{\pi t}{12}\\\\\textrm{So the function is:}}\\\\f(t) = 2 \sin \left(\dfrac{\pi t}{12}\right)\)
1. The amplitude is 2 and this is the maximum water level in feet at the beach. This occurs when \(\textstyle {\dfrac{\pi t }{12} = \dfrac{\pi}{2}}\)
or, when t = 6. It repeats every 24 hours (see #2)
2. The periodicity of a function is when the function starts repeating itself
The periodicity of sin(x) is 2π i.e. the sinusoidal wave starts repeating itself every 2π radians
Since our sine function has πt/12 as its argument we have that
πt/12 = 2π
or t = 24
So every 24 hours, the water level which starts at 0 feet at 0 hours, becomes 0 again
3) Graph of the function attached. Note that water level cannot be negative which is the sine value from π/2 to 2π so we have to set it equal to 0
Water level goes to zero every 12 hours and stays at zero for 12 hours when it starts rising again.
As can be seen from the graph, every 24 hours, the water level reaches a peak height of 2 feet
I hope that this helps
![The water level f, in feet, at a certain beach is modeled by the function [tex]f(t)=2sin(2\pi t)/24[/tex],](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/wKazcLEYOqiqrwmV9t8w94KBpUTOwMUX.png)
the mariana trench is about 11km deep. mount everest is about 29,000 ft high. what is the total height change from the top of mount everest to the bottom of the mariana trench, expressed in miles?
Answers
Using unit conversions the total height change from the top of mount Everest to the bottom of the Mariana trench is 12.3 miles
We know that 1 km = 0.62136 miles and 1 foot = 0.000189 miles
Depth of Mariana Trench (d) = 11 km = 11 × 0.62136
= 6.835 miles
Height of Mount Everest (h) = 29000 ft = 29000 × 0.000189
= 5.492 miles
Therefore the total height difference top of Mount Everest and to bottom of the Mariana Trench is given by
H = Depth of Mariana Trench + Height of Mount Everest
H = d + h
H = 6.835 miles + 5.492 miles
H = 12.327 miles
H = 12.3 miles
To learn more about unit conversions here:
brainly.com/question/19420601
#SPJ4
convolution, Fourier series representation problems
w 32. Use the convolution theorem to solve the integral equation: y(t) = ? + - sinhít – sinh(t - A)g()dx 33. Find the Fourier series representation of f(x) given that f(x) = -{: -1, - < x < 0 , 0
Answers
32. Solving integral equation using the convolution theoremThe convolution theorem states that the convolution of two signals in the time domain is equivalent to multiplication in the frequency domain.
Therefore, to solve the given integral equation using the convolution theorem, we need to take the Fourier transform of both sides of the equation.
y(t) = ∫_{-∞}^{∞} sinh(−)g() + ∫_{-∞}^{∞} sinh(−−)g()Taking the Fourier transform of both sides, we haveY() = 2π[G()sinh() + G()sinh(−)]where Y() and G() are the Fourier transforms of y(t) and g(t), respectively.Rearranging for y(t), we gety(t) = (1/2π) ∫_{-∞}^{∞} [G()sinh()+G()sinh(−)]e^(j) d= (1/2π) ∫_{-∞}^{∞} [G()sinh()+G()sinh(−)](cos()+j sin())d= (1/2π) ∫_{-∞}^{∞} [G()sinh()+G()sinh(−)]cos()d+ j(1/2π) ∫_{-∞}^{∞} [G()sinh()+G()sinh(−)]sin()dTherefore, the solution to the integral equation is given by:y(t) = (1/2π) ∫_{-∞}^{∞} [G()sinh()+G()sinh(−)]cos()d + (1/2π) ∫_{-∞}^{∞} [G()sinh()+G()sinh(−)]sin()d
It is always important to understand the principles that govern an integral equation before attempting to solve them. In this case, we used the convolution theorem to solve the equation by taking the Fourier transform of both sides of the equation and rearranging for the unknown signal. The steps outlined above provide a comprehensive solution to the equation. 33. Fourier series representation of f(x)
The Fourier series representation of a periodic signal is an expansion of the signal into an infinite sum of sines and cosines. To find the Fourier series representation of the given signal, we need to first compute the Fourier coefficients, which are given by:an = (1/T) ∫_{-T/2}^{T/2} f(x)cos(nx/T) dxbn = (1/T) ∫_{-T/2}^{T/2} f(x)sin(nx/T) dxFurthermore, the Fourier series representation is given by:f(x) = a_0/2 + Σ_{n=1}^{∞} a_n cos(nx/T) + b_n sin(nx/T)where a_0, a_n, and b_n are the DC and Fourier coefficients, respectively. In this case, the signal is given as:f(x) = -1, -π
To know more about integral visit
https://brainly.com/question/31433890
#SPJ11
5. Theresa decides to donate money to cancer
research each year. Her brother, Tony, also decides
to contribute. Together, they donate $1,000 per
year to cancer research. If Tony is able to donate
1 1/2 times the amount that Theresa is able to
donate, what is the amount in dollars that Tony
will donate after 5 years, assuming the amount
and proportions remain the same cach year?
A. $2.000
B. $2.100
C. $2.450
D. $3.000
E. $3.600
Answers
Answer:
3000
Step-by-step explanation:
Tony will donates $3000 after 5 years.
What is Algebra?A branch of mathematics known as algebra deals with symbols and the mathematical operations performed on them.
Variables are the name given to these symbols because they lack set values.
In order to determine the values, these symbols are also subjected to various addition, subtraction, multiplication, and division arithmetic operations.
Given:
Donated amount= $1000
Tony is able to donate 3/2 times the amount that Theresa donates.
let Theresa donates x dollar each year
So, x+ 3/2x = 1000
5x/2 = 1000
5x = 2000
x= 400
Thus, Tony donate = 3/2 x 400 = $600
Hence, After 5 years Tony will donate= 600 x 5= $3000
Learn more about Algebra here:
https://brainly.com/question/24875240
#SPJ5
Explain what is meant by confounding. what is a lurking variable? what is a confounding variable?
Answers
Explain what is meant by confounding. what is a lurking variable? what is a confounding variable?
Answer:
A Confounding is the variable that is considered in a research study, and could overall influence the relations between the variables in the study. For example, students wanting to join AP English next semester were told to write a six page essay. When the students turned in their papers and teachers say the difference and grades they believed that the variable was the time that the students handed in the paper. They thought that if the student handed in their paper later than another student that they would receive a lower score, but this was not the case. When asking the students how they prepared for the paper, students replied with different answers. Those who outlined and used other literature for reference scored much higher than those who only used prior knowledge to write their essays. In this study, the lurking variable would be the presence of an outline.
Lurking variable: A variable that is not considered in a research study that could influence the relations between the variables in the study
Confounding variable: A variable that is considered in a research study that could influence the relations between the variables in the study
To Know more about Confounding Variable
https://brainly.com/question/28481575
can anyone help me, I'm trying to check my son's homework

Answers
To determine the distance between the Party supply store and the art gallery, you have to determine the position of each store and subtract them.
The stores are in the same horizontal line (y=2), the supply store is at x₁=1 and the art gallery is at x₂=7, the distance (d₁) between both stores can be calculated as:
\(\begin{gathered} d_1=x_2-x_1 \\ d_1=7-1 \\ d_1=6 \end{gathered}\)The distance between the party supply store and the art gallery is 6 blocks.
Next you have to determine the distance between the art gallery and the dry cleaners. Both stores are on the same vertical line (x=7), to calculate the distance you have to determine the difference between their positions over the y-axis.
The art gallery is at y₁=2 and the dry cleaners is at y₂=7. The distance between both stores (d₂) can be calculated as:
\(\begin{gathered} d_2=y_2-y_1 \\ d_2=7-2 \\ d_2=5 \end{gathered}\)The dry cleaner is 5 blocks away from the art gallery.
Now add both distances to determine how far would you walk
\(d_1+d_2=6+5=11\)The distance walked is 11 blocks
find the height of a pyramid with the volume of 340 cubic inches and a base of 42.5 squared inches.
Answers
Answer:
24 in
Step-by-step explanation:
The volume of a pyramid of base area A and height h is V = (1/3)(A)(h).
It's easiest to solve this for h before plugging in numerical values. Solving for h, we get: 3V = A·h, or
3V
h = -------------
A
With A = 42.5 in² and V = 340 in³, we have
3(340 in³)
h = ---------------- = 24 in
42.5 in²
V = --------------
two rays sharing a common endpoint is the definition of which term?
Answers
Two rays sharing a common endpoint is the definition of an angle.
What is a Ray?A ray is a geometric shape that is defined by a starting point (or endpoint) and extends infinitely in one direction. It is represented by an arrowhead on one end, indicating the direction of the ray. It is a one-dimensional object, and it can be thought of as a line with one endpoint fixed and the other extending indefinitely.
What is an Angle?An angle is defined as the measure of the amount of rotation between two rays that share a common endpoint (or vertex). The common endpoint is called the vertex of the angle. The two rays are called the arms of the angle.
Thus, two rays form an angle.
Learn more about rays on:
https://brainly.com/question/1734531
#SPJ1
Graph the system of equations. y = 2x y = –x + 6 Two lines on a coordinate plane that intersect at the point 2 comma 4. One line has y intercept 0 and the other has y intercept 6. Two lines on a coordinate plane that intersect at the point negative 2 comma negative 4. One line has y intercept 0 and the other has y intercept negative 6. Two lines on a coordinate plane that intersect at the point 1 comma 2. One line has y intercept 0 and the other has y intercept 3. Two lines on a coordinate plane that intersect at the point 3 comma 3. One line has y intercept 0 and the other has y intercept 6.
Answers
The solution to the systems of equations graphically is (2, 4)
Solving the systems of equations graphicallyFrom the question, we have the following parameters that can be used in our computation:
y = 2x
y = -x + 6
Next, we plot the graph of the system of the equations
See attachment for the graph
From the graph, we have solution to the system to be the point of intersection of the lines
This points are located at (2, 4)
Read more about equations at
brainly.com/question/148035
#SPJ1

a closed cylindrical can has a fixed surface area s. find the ratio of its height to the diameter of its base that maximizes its volume.
Answers
The ratio of the height to the diameter that maximizes the volume of the cylindrical can is: 0.886 approximately.
Let the radius of the cylindrical can be denoted by r, and its height by h. The surface area of the can is given by:
S = 2π\(r^2\)+ 2πrh
Simplifying this expression, we get:
h = (S - 2π\(r^2\))/(2πr)
The volume of the cylindrical can is given by:
V = π\(r^2\)h
Substituting the expression for h obtained earlier, we get:
V = π\(r^2\)(S - 2π\(r^2\))/(2πr)
Simplifying this expression, we get:
V = (S/2π - \(r^2\))πr
To maximize the volume of the cylindrical can, we need to find the value of r that maximizes the above expression. We can do this by differentiating the expression with respect to r, setting it equal to zero, and solving for r:
dV/dr = (S/2π - \(2r^2\))π = 0
Solving for r, we get:
r = √(S/4π)
Substituting this value of r back into the expression for h, we get:
h = (S - 4π\(r^2\))/(4πr) = (S - S/2)/(2√(S/4π)) = √(Sπ)/2
Therefore, the ratio of the height to the diameter that maximizes the volume of the cylindrical can is:
h/2r = (√(Sπ)/2)/(2√(S/4π)) = √(π/4) = 0.886 approximately.
To learn more about cylindrical visit: https://brainly.com/question/28231934
#SPJ11
Solve this (algebra) to the simplest form

Answers
Answer: b to the power of 3 / 8 Have a nice day!
change the following to algebraic expressions
nine times a number decreased by 11
Answers
Step-by-step explanation:
let the number be X
so,
X^9 - 11
Answer: the answer is -4
What is an equation of the line that passes through the point (-6, -7) and is
perpendicular to the line 6x + 5y = 30?
Answers
Answer:
Step-by-step explanation:
Product of slope of perpendicular lines = -1
6x + 5y = 30
Write this equation in y = mx + b form
5y = -6x + 30
y = \(\frac{-6}{5}x+\frac{30}{5}\)
\(y=\frac{-6}{5}x + 6\)
Slope of this line m₁ = -6/5
m₁ * m₂ = -1
m₂ = -1÷m₁ = -1 * \(\frac{5}{-6}\)
\(m_{2}=\frac{5}{6}\) & (-6 , -7)
Equation of the required line: y - y₁ = m (x - x₁)
\(y - (-7) = \frac{5}{6}(x - [-6])\\\\y + 7 = \frac{5}{6}x + 6 *\frac{5}{6}\\\\y = \frac{5}{6}x +5-7\\\\y=\frac{5}{6}x-2\)
What is the range of f/x )= sin x the set of all real numbers?
Answers
On solving the provided question we can say that - The Range of the given function, f(x) = sin(x) , Range = \(-1 < y < 1\)
What is Range?Range: the discrepancy between the top and bottom numbers. To get the range, locate the greatest observed value of the variable and deduct the least observed value (the minimum). The data points between the two extremes of the distribution are not taken into consideration by the range; just these two values are considered. Between the lowest and greatest numbers, there is a range. Values at the extremes make up the range. The data set 4, 6, 10, 15, 18, for instance, has a range of 18-4 = 14, a maximum of 18, a minimum of 4, and a minimum of 4.
The Range of the given function, f(x) = sin(x)
\(-1 < y < 1\)
To know more about Range visit:
https://brainly.com/question/12789483
#SPJ4
Challenge The price of Stock A at 9 AM. was $14.62. Since then, the price has been increasing at the rate of $0.13 each hour. At noon the price of Stock B was $15.37. It begins to decrease at the rate
of $0.15 each hour. If the two rates continue, in how many hours will the prices of the two stocks be the same?
Answers
After 2.68 hours the price of both stocks be the same.
What is stock?A stock denotes an investment to the public company. The term stock is used to confirm the certificate of all shareholders who invested for a large company.
What is stock price?The word stock price refers the current value or market price. price can be dropped or extended or remain the same.
Given, The price of stock A at 9AM =$14.62
since then, this price start increasing $0.13 per hour
At noon the price of Stock B =$15.37
since then, this price start decreasing $0.15 per hour
let, it takes x hours that the prices of both stocks become equal.
after x hour the stock A become $14.62+$0.13x
after x hours the stock B become $15.37-$0.15x
as per given statement, 14.62+0.13x = 15.37-0.15x
solving equation, we get x=2.68
hence, after 2.68 hours the price of both stocks be the same.
to learn more about price of stock visit:
https://brainly.com/question/19091385
#SPJ1
Answer:
1 2/7 hours (after noon)
Step-by-step explanation:
You want to know how long after noon two stocks will have the same price if A was $14.62 at 9 a.m. and increasing $0.13 per hour, while B was $15.37 at noon and decreasing $0.15 per hour.
SetupIf x represents hours after midnight, the price of stock A can be described by ...
A = 14.62 +0.13(x -9)
and the price of stock B can be described by ...
B = 15.37 -0.15(x -12)
SolutionThe two prices will be the same when ...
A = B
14.62 +0.13(x -9) = 15.37 -0.15x -12 . . . . . substitute for A and B
0.13x +13.45 = -0.15x +17.17
0.28x = 3.72 . . . . . . . . . add 0.15x-13.45
x = 3.72/0.28 = 13 2/7 . . . . . . hours after midnight
To find the number of hours after noon, we need to subtract 12 from this number. 13 2/7 -12 = 1 2/7
The two stocks will be the same price after 1 2/7 hours.
__
Additional comment
That's about 1:17 p.m.
The wording "in how many hours" is a bit ambiguous, since there are two different time references given in the problem. We assume we want hours after the later time reference, noon.
Fiona earns 85 cents for each toy she
a- How much does she earn for assembling:
i) 146 toys? ii) 203 toys?
b- Last week Fiona earned $459
How many tovs did she assemble?
c- Find the number of toys Fiona must assemble to earn (at least)
the following amounts:
i) $200
ii) $620
Please explain and with steps
Answers
Given :
Cost of each toy assembled by Fiona = 85 centsa) total amount of money she earns for assembling
(i)146 toys= cost of one toy x no. of toys she assembled= 85cents x 146= 12,410 cents or $124.10 (ii)203 toys= cost of one toy x no. of toys she assembled= 85cents x 203= 17,255 cents or $172.55b) total no. of toys assembled by Fiona by earning:
$459convert $459 into cents
$459 = 459 x 100 = 45,900 centsdivide the sum by the cost of a single toy
= 45900cents/85cents= 540 toyshence, she assembled 540 toys and earned $459 out of them.
c) no. of toys she must assemble to earn
(i) $200convert the sum into cents
$200 = 20,000 centsdivide the sum by the cost of a single toy
20,000cents/85cents= 235 toyshence, she must assemble 235 toys in order to earn $200
(ii) $620convert the sum into cents
$620 x 100 = 62,000 centsdivide the sum by the cost of a single toy
62,000cents/85cenfs= 729 toyshence,she must assemble 729 toys in order to earn $620
When a scientist conducted a genetics experiments with peas, one sample of offspring consisted of 933 peas, with 729 of them having red flowers. If we assume, as the scientist did, that under these circumstances, there is a 3/4 probability that a pea will have a red flower, we would expect that 699.75 (or about 700) of the peas would have red flowers, so the result of 729 peas with red flowers is more than expected.
. If the scientist's assumed probability is correct, find the probability of getting 729 or more peas with red flowers.
b. Is 729 peas with red flowers significantly high?
c. What do these results suggest about the scientist's assumption that 3/4 of peas will have red flowers
Answers
The solution to the statistics have been given below
How to solve for the probabilityThe probability = 3 / 4 = 0.75
n = 933
x≥ 729
np = 0.75 * 933
= 699.75
√933 * 0.75 * 0.25
= √174.9375
= 13.23
using the continuity correction we have
729 - 0.5
= 728.5 - 699.75 / 13.23
= 2.17
The p value is 0.015003.
there is a 1.5% chance of getting 729 peas with red flowers
b. given that Z is greater than 2, this can be said to be high
c. These results suggest that the scientist maybe wrong in his assumption
Read more on statistics here:https://brainly.com/question/25082768
#SPJ1
Find the integer that exceeds –5 by the same amount that 13 exceeds –1. \
Answers
Answer:
7
Step-by-step explanation:
13 exceeds - 1 by - 1 + 13 = 12, then
- 5 + 12 = 7
Answer:
Step-by-step explanation:
Answer:
7
Step-by-step explanation:
13 exceeds - 1 by - 1 + 13 = 12, then
- 5 + 12 = 7
some students took an optional training class before their driving test. 28/75 took the optional class and passed their drivers test. 8/15 passed their drivers test. 3/5 took the optional class. How many students took the optional class, given he or she passed?
Answers
Approximately 17 students who took the optional class passed their driver's test.
Let's solve this problem step by step.
We are given the following information:
28 out of 75 students who took the optional class passed their driver's test.
8 out of 15 students overall passed their driver's test.
3 out of 5 students took the optional class.
To find the number of students who took the optional class and passed, we need to calculate the intersection of these two groups.
First, let's calculate the total number of students who took the optional class:
Total students who took the optional class = (3/5) \(\times\) Total number of students
Total students who took the optional class = (3/5) \(\times\) 75 = 45
Now, let's calculate the total number of students who passed their driver's test:
Total students who passed their driver's test = (8/15) \(\times\) Total number of students
Total students who passed their driver's test = (8/15) \(\times\) 75 = 40
Next, let's find the number of students who both took the optional class and passed their driver's test.
This can be found by taking the intersection of the two groups:
Number of students who took the optional class and passed = (28/75) \(\times\)Total students who took the optional class
Number of students who took the optional class and passed = (28/75) \(\times\)45 = 16.8 (approximated to the nearest whole number).
Therefore, approximately 17 students who took the optional class passed their driver's test.
It's important to note that since we're dealing with whole numbers, the approximated answer is 17, as we cannot have a fraction of a student.
For similar question on intersection.
https://brainly.com/question/30915785
#SPJ8
if m, p, and t are distinct positive prime numbers, then m3pt has how many different positive divisors greater than 1 ?
Answers
There are 15 different positive divisors (greater than 1) for the number m³pt. Here m, p, and t are distinct prime numbers. This is obtained by the prime factorization method.
How to find the number of positive factors for a number?The following are the steps to find the number of positive factors of a number:
Step 1: Find the L.C.M of the number by using the prime factorization method. For example: consider the number 24. Then, its prime factorization is as follows:
24 = 2 × 2 × 2 × 3
Step 2: Same bases should be added in powers. So, the factors we can write as
24 = 2³ × 3¹
Step 3: To find the number of positive factors of the number, the exponents of the prime factors is multiplied by adding 1.
I,e., N = (3 + 1)(1 + 1) = 4 × 2 = 8.
So, there are 8 factors for the number 32. They are 1, 2, 3, 4, 6, 8, 12, and 24.
Calculation:It is given that, m, p, and t are distinct positive prime numbers.
Then, the number of positive divisors greater than 1 for the number m³pt are
m³× p × t
Since m, p, and t are prime factors, we can multiply their power by adding 1 to them. I.e.,
N = (3 + 1) (1 + 1) (1 + 1) = 4 × 2 × 2 = 16
So, there are a total of 16 factors for the given number (including 1). So, the number of factors greater than 1 is 16 - 1 = 15.
Therefore, there are 15 different positive divisors greater than 1 for the number having prime factors as m³pt.
Learn more about prime factorization and the number of factors formula at the following link:
https://brainly.com/question/16358473
#SPJ4
An African elephant weighs 6.3 tons. Convert the weight to pounds.
Answers
Multiply by 2000
6.3 * 2000= 12600
The diameter of a circle is 12.8 meters. What is the circle's circumference?
Answers
Answer:
40.21 m is the circle's cirumference.