Answers
Answer:
5
Step-by-step explanation:
First find the value of 1/10 of 500 :
⇒ 1/10 × 500
⇒ 500/10
⇒ 50
Now divide 50 by 10 to get the missing value :
⇒ 50/10
⇒ 5
Related Questions
Pleaseeeee helpppppp meee

Answers
Answer:
C, F
Step-by-step explanation:
Dont have time rn
find a ratio that is
equivalent to 2:5.
Answers
Answer:
4:10 hope this helps
Step-by-step explanation:
coordinate plane with points at A 0 comma 2 and B 2 comma 0 intersected by line f Dilate line f by a scale factor of one half with the center of dilation at the origin to create line f′. Where are points A′ and B′ located after dilation, and how are lines f and f′ related? The locations of A′ and B′ are A′ (0, 2) and B′ (0, 0); lines f and f′ intersect at point A. The locations of A′ and B′ are A′ (0, 1) and B′ (1, 0); lines f and f′ are parallel. The locations of A′ and B′ are A′ (0, 0) and B′ (2, 0); lines f and f′ intersect at point B. The locations of A′ and B′ are A′ (0, 2) and B′ (2, 0); lines f and f′ are the same line.
Answers
The answer of the given question based on the graph is , The locations of A′ and B′ are A′ (0, 1) and B′ (1, 0); lines f and f′ are parallel.
What is Scale factor?A scale factor is a number that scales, or multiplies, a quantity by some factor. It is used in mathematics to describe the relationship between corresponding measurements of two similar figures, such as triangles or rectangles.
To dilate line f by scale factor of one half with center of dilation at origin, we multiply coordinates of each point on line f by 1/2.
The equation of line f can be found by using the points A and B:
slope of line f = (0 - 2)/(2 - 0) = -1
y-intercept of line f = 2
Therefore, the equation of line f is y = -x + 2.
To find the coordinates of A' and B' after dilation, we can apply the dilation factor to each point:
A' = (0, 2)*1/2 =(0, 1)
B' = (2, 0)*1/2 =(1, 0)
So A' is located at (0, 1) and B' is located at (1, 0) after dilation.
Now let's analyze the relationship between lines f and f'. The dilation was centered at the origin, so the origin is a fixed point of the dilation. This means that the point where lines f and f' intersect must be the origin.
If we plug in x = 0 into the equation of line f, we get y = 2. This means that point A is located at (0, 2) and intersects with line f at y = 2. After dilation, point A' is located at (0, 1), which means that lines f and f' intersect at point A.
To determine the relationship between lines f and f', we can compare their equations. The equation of f' can be found by using the points A' and B':
slope of f' = (0 - 1)/(1 - 0) = -1
y-intercept of f' = 0
Therefore, the equation of f' is y = -x.
Comparing the equations of f and f', we can see that they have the same slope of -1, which means they are parallel. Therefore, the correct answer is: The locations of A′ and B′ are A′ (0, 1) and B′ (1, 0); lines f and f′ are parallel.
To know more about Center of dilation visit:
https://brainly.com/question/30240999
#SPJ1
Which of the scenarios below are considered seller-based discounts? options are in the picture

Answers
The scenarios that can be considered a seller-based discount are:
A. The offer by Wire and Cable
B. Carfna's Fine Foods
C. Mouser Electronics offer
E. Carchex Car Maintenance
What is a seller-based discount?A seller-based discount is a discount that is offered by a seller for the early purchase of a product. The goal of the seller in this case is to get cash as he or she is in an immediate need for cash.
The most outstanding example is that of Carchex Car Maintenance where an offer is made by the seller for the early purchase of products.
Learn more about the seller-based discount here:
https://brainly.com/question/30849708
#SPJ1
Joy sells two types of yarn: wool and synthetic. Wool is $12 per skein and synthetic is $9 per skein. If Joy sold 16 skeins of synthetic and collected a total of $432, how many skeins of wool did she sell?
Answers
multiple the amount of synthetic skeins sold to the price of one synthetic skein. subtract the sum to the total. take the subtracted sum and divide it by the price of wool skeins
Explanation:
First you have to see how much of the money she has total came from the synthetic yarn profit.
If she sold 16 skeins of synthetic yarn you multiply 16 x 9(the price per skein of synthetic yarn) to get 144.
Next you subtract 144 from 432 (432-144) to get 288.
Finally, divide 288 by 12(the price of a skein of wool yarn) to get 24.
24 is the amount of skeins of wool yarn she sold.
To be sure you can multiply 24 x 12 (wool yarn sold) and add that to 16 x 9 (synthetic yarn sold) to get 432 which is your total profit.
Hope this helps!
Each of the triangles below has one angle measured. Mentally estimate the measures of the other two angles. Drag and drop the most likely angle measurements to the two different angles in each triangle. I forgot to upload the picture in the other thing, so please help me. I need this to be an A+

Answers
Answer:
Step-by-step explanation:
presumably this is the answer and if you want the reasoning I could explain it in more detail if needed
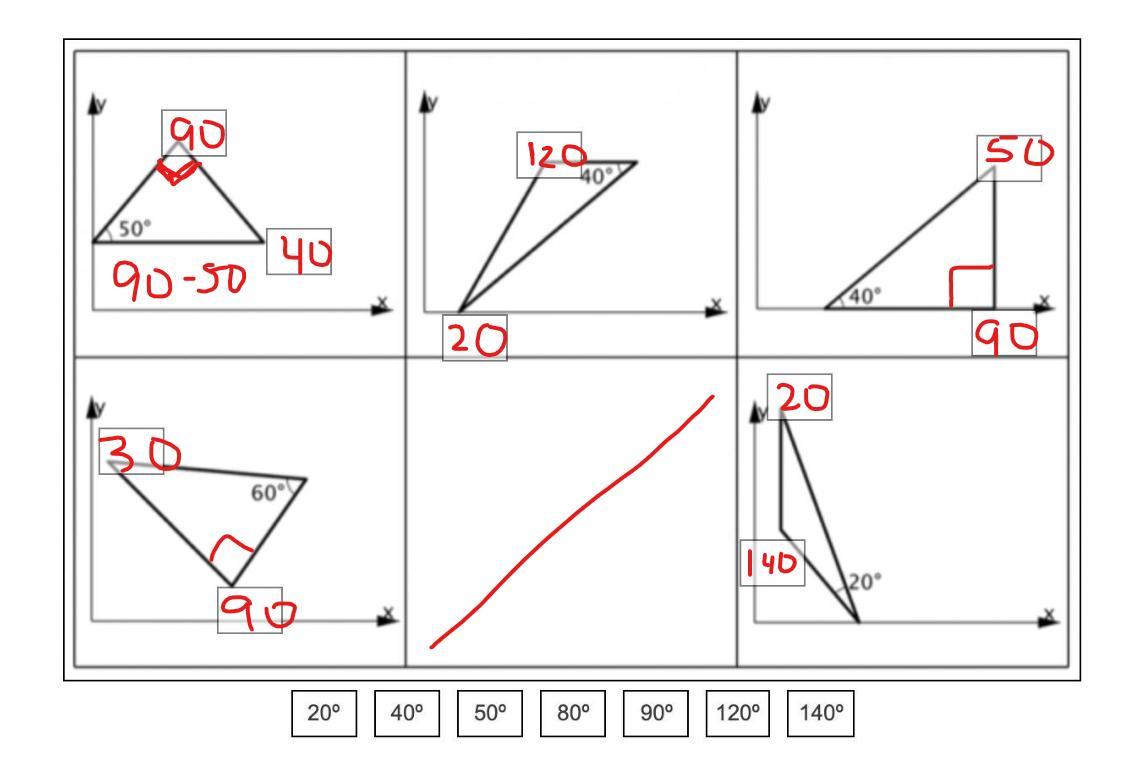
please please help me I will mark brainlist !!



Answers
Answer:
9. B. 32 millimeters
10. C. 7 inches
11. C. 56.24 millimeters
13. B. 14.13 square feet
Step-by-step explanation:
9. Radius of a circle or any circular shape = ½ of its diameter
Diameter of the disk = 64 millimeters
Radius of the disk = ½(64) = 32 millimeters
10. Width of the cooler = 6 in.
Length = 8 in.
Volume = 336 in.³
Height = ?
Formula for volume of a rectangular prism = L*W*H
Plug in the values
336 = 8*6*H
336 = 48*H
Divide both sides by 48
336/48 = H
H = 7 inches
11. A dime has a circular shape
The circumference of the dime = circumference of a circle = πd
Where,
d = 17.91 millimeters
π = 3.14
Plug in the values
C = 3.14 × 17.91 = 56.2374
≈ 56.24 millimeters (nearest hundredth)
12. Area of the top of the desk = area of semicircle = ½ × πr²
Where,
r = ½(6) = 3 ft
π = 3.14
Plug in the values
Area = ½ × 3.14 × 3² = ½ × 3.14 × 9
Area = 14.13 square feet
A triangle has vertices at (1, 1), (1, 4), and (-3, 4).
What are the coordinates of the centroid?
Answers
Answer:
B, (-1/3, 3)
Step-by-step explanation:
This is the correct answer :)
Answer:
B, (-1/3, 3)
Step-by-step explanation:
For the following vectors, (a) find the dot product v•w ; (b) find the angle between v and w , (c) state whether the vectors are parallel, octagonal, or neither. V=-3i-4j, w=6i+8j
A- v•w
B-the angle between v and w is theta ^•?
C- the vectors v and w are?
Answers
B) The angle between vectors v and w can be found using the formula: cos(theta) = (v • w) / (||v|| ||w||), where ||v|| and ||w|| are the magnitudes of vectors v and w respectively.
First, we need to find ||v|| and ||w||:
||v|| = sqrt((-3)^2 + (-4)^2) = 5
||w|| = sqrt((6)^2 + (8)^2) = 10
Now, we can substitute in the values to get:
cos(theta) = (-50) / (5 * 10) = -1
theta = arccos(-1) = pi radians or 180 degrees.
Therefore, the angle between vectors v and w is 180 degrees.
C) Two vectors are parallel if their directions are the same, which can be determined by comparing their unit vectors.
The unit vector of v is:
v_hat = v / ||v|| = (-3/5)i + (-4/5)j
The unit vector of w is:
w_hat = w / ||w|| = (6/10)i + (8/10)j = (3/5)i + (4/5)j
We can see that the unit vectors are in opposite directions, which means that the vectors are anti-parallel or opposite. Therefore, the vectors v and w are neither parallel nor orthogonal.
Find the sum of the following fractions:
2/8 + 1/3
Answers
Answer:
Step-by-step explanation:
Answer:
7/12. if you find a common denominator for the two, like 24 for example, 2/8 converts to 6/24 and 1/3 converts to 8/24. 6/24+8/24=14/24, and that reduced is 7/12.
Step-by-step explanation:
The coordinates of the midpoints of the four sides of a square are S(-4,11), Q(2,5), U(-4,-1), A (-10,5)
Answers
The perimeter and area of the square are; 24√2 units and 12 units² respectively
Given the coordinates of the midpoints of the four sides of a square are S(-4,11), Q(2,5), U(-4,-1), A (-10,5)
But since we have the midpoints of all the sides, we can assume they're equidistant from one another since the figure is a square.
SQ = √(x₂ - x₁)² + (y₂ - y₁)²
SQ = √(2 - (-4)² + (5 - 11)²
SQ = 6√2
Let's find QU
QU = √(-4 - 2)² + (-1 - 5)²
QU = 6√2
Let's find UA ;
UA = √(-10 - (-4))² - (5 - (-1)²
UA = 6√2
And the distance AS = 6√2
The perimeter of the square = 4 (6√2)
Perimeter = 24√2 units
The area of the square = l²
Area of the square = (6√2)²
Area of square = 12 units²
Learn more on perimeter of square here;
brainly.com/question/25092270
#SPJ1
Rewriting 3x^2=6x and solving with rewritten
Answers
Answer:
x = 0 , x = 2
Step-by-step explanation:
3x² = 6x ( subtract 6x from both sides )
3x² - 6x = 0 ← factor out 3x from each term
3x(x - 2) = 0
equate each factor to zero and solve for x
3x = 0 ⇒ x = 0
x - 2 = 0 ( add 2 to both sides )
x = 2
solutions are x = 0 , x = 2
In an isolated environment, a disease spreads at a rate proportional to the product of the infected and non-infected populations. Let I(t) denote the number of infected individuals. Suppose that the total population is 2000, the proportionality constant is 0.0001, and that 1% of the population is infected at time t-0, write down the intial value problem and the solution I(t).
dI/dt =
1(0) =
I(t) =
symbolic formatting help
Answers
Answer:
dI/dt = 0.0001(2000 - I)I
I(0) = 20
\(I(t)=\frac{2000}{1+99e^{-0.2t}}\)
Step-by-step explanation:
It is given in the question that the rate of spread of the disease is proportional to the product of the non infected and the infected population.
Also given I(t) is the number of the infected individual at a time t.
\(\frac{dI}{dt}\propto \textup{ the product of the infected and the non infected populations}\)
Given total population is 2000. So the non infected population = 2000 - I.
\(\frac{dI}{dt}\propto (2000-I)I\\\frac{dI}{dt}=k (2000-I)I, \ \textup{ k is proportionality constant.}\\\textup{Since}\ k = 0.0001\\ \therefore \frac{dI}{dt}=0.0001 (2000-I)I\)
Now, I(0) is the number of infected persons at time t = 0.
So, I(0) = 1% of 2000
= 20
Now, we have dI/dt = 0.0001(2000 - I)I and I(0) = 20
\(\frac{dI}{dt}=0.0001(2000-I)I\\\frac{dI}{(2000-I)I}=0.0001 dt\\\left ( \frac{1}{2000I}-\frac{1}{2000(I-2000)} \right )dI=0.0001dt\\\frac{dI}{2000I}-\frac{dI}{2000(I-2000)}=0.0001dt\\\textup{Integrating we get},\\\frac{lnI}{2000}-\frac{ln(I-2000)}{2000}=0.0001t+k \ \ \ (k \text{ is constant})\\ln\left ( \frac{I}{I-222} \right )=0.2t+2000k\)
\(\frac{I}{I-2000}=Ae^{0.2t}\\\frac{I-2000}{I}=Be^{-0.2t}\\\frac{2000}{I}=1-Be^{-0.2t}\\I(t)=\frac{2000}{1-Be^{-0.2t}}\textup{Now we have}, I(0)=20\\\frac{2000}{1-B}=20\\\frac{100}{1-B}=1\\B=-99\\ \therefore I(t)=\frac{2000}{1+99e^{-0.2t}}\)
The required expressions are presented below:
Differential equation\(\frac{dI}{dt} = 0.0001\cdot I\cdot (2000-I)\) \(\blacksquare\)
Initial value\(I(0) = \frac{1}{100}\) \(\blacksquare\)
Solution of the differential equation\(I(t) = \frac{20\cdot e^{\frac{t}{5} }}{1+20\cdot e^{\frac{t}{5} }}\) \(\blacksquare\)
Analysis of an ordinary differential equation for the spread of a disease in an isolated population
After reading the statement, we obtain the following differential equation:
\(\frac{dI}{dt} = k\cdot I\cdot (n-I)\) (1)
Where:
\(k\) - Proportionality constant\(I\) - Number of infected individuals\(n\) - Total population\(\frac{dI}{dt}\) - Rate of change of the infected population.Then, we solve the expression by variable separation and partial fraction integration:
\(\frac{1}{k} \int {\frac{dI}{I\cdot (n-I)} } = \int {dt}\)
\(\frac{1}{k\cdot n} \int {\frac{dl}{l} } + \frac{1}{kn}\int {\frac{dI}{n-I} } = \int {dt}\)
\(\frac{1}{k\cdot n} \cdot \ln |I| -\frac{1}{k\cdot n}\cdot \ln|n-I| = t + C\)
\(\frac{1}{k\cdot n}\cdot \ln \left|\frac{I}{n-I} \right| = C\cdot e^{k\cdot n \cdot t}\)
\(I(t) = \frac{n\cdot C\cdot e^{k\cdot n\cdot t}}{1+C\cdot e^{k\cdot n \cdot t}}\), where \(C = \frac{I_{o}}{n}\) (2, 3)
Note - Please notice that \(I_{o}\) is the initial infected population.
If we know that \(n = 2000\), \(k = 0.0001\) and \(I_{o} = 20\), then we have the following set of expressions:
Differential equation\(\frac{dI}{dt} = 0.0001\cdot I\cdot (2000-I)\) \(\blacksquare\)
Initial value\(I(0) = \frac{1}{100}\) \(\blacksquare\)
Solution of the differential equation\(I(t) = \frac{20\cdot e^{\frac{t}{5} }}{1+20\cdot e^{\frac{t}{5} }}\) \(\blacksquare\)
To learn more on differential equations, we kindly invite to check this verified question: https://brainly.com/question/1164377
If one wanted to solve the equation below using the quadratic formula, what would be the b value used to substitute into the quadratic equation.
3x 2 − 2 = - 5x
Answers
Answer:
b = 5
Step-by-step explanation:
All quadratic equations are formed in the format of \(a^{2}\) + bx + c = 0
Using this formula, we can re-arrange the equation to fit the given format.
\(3x^{2}\) - 2 = -5x
\(3x^{2}\) + 5x - 2 = 0
5 is plugged in for "b" in this equation, therefore b = 5.
Please help, I'm really confused and would really appreciate the help. What is the measure of angle R and how do I find it?
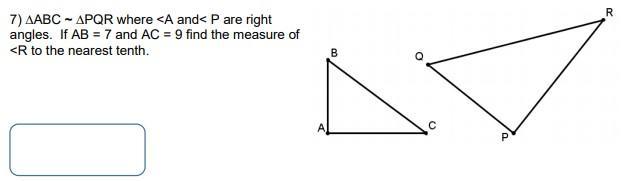
Answers
Answer:
37.9°
Step-by-step explanation:
ΔABC is similar to ΔPQR, so ∠R ≅ ∠C.
Given AB = 7 and AC = 9, we can find m∠C using tangent.
tan C = AB / AC
tan C = 7 / 9
m∠C = 37.9°
m∠R = 37.9°
Enter the ratio as a fraction in lowest terms.
5 ft to 70 in.
Answers
Answer:
1/14
Step-by-step explanation:
The ratio is 5:70. The fraction form of that is 5/70. To get the lowest terms, I divided both numbers by 5. So it is 1/14
which relation describes the graph?

Answers
Answer:
B.
Step-by-step explanation:
someone please help me answer this!!
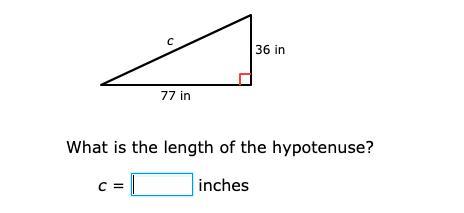
Answers
Answer:
c = 85 in is the answer.
Step-by-step explanation:
a = 36 in
b = 77 in
c = ?
According to the Pythagoras theorem,
a² + b² = c²
36² + 77² = c²
1296 + 5929 = c²
7225 = c²
c = 85 in
∴ c = 85 in is the length of the missing leg.
36^2+77^2=c^2
1296+5929=c^2
C^2=7225
C=-_/7225
C=85
Bookwork code: N84
This is a new version of the question Make sure you start now workings
Calculate the range, in centimetres (cm), of the following
lengths:
15 cm, 0.5 cm, 10.3 cm, 16.7 cm, 21 cm,
8.6 cm
Answers
The range, in centimetres (cm), of the following lengths is 20.5 cm
What is the range?
The difference between the lowest and highest numbers is referred to as the range. For instance, the range will be 10 - 2 = 8 if the given data set is 2, 5, 8, 10, and 3.
As a result, the range may alternatively be thought of as the distance between the highest and lowest observation. The range of observation is the name given to the outcome. Statistics' range reflects the variety of observations.
Given, 15 cm, 0.5 cm, 10.3 cm, 16.7 cm, 21 cm, 8.6 cm
So, the highest value of length = 21 cm
the lowest value of length = 0.5 cm
Then, range = the highest value - the lowest value
= 21 - 0.5 = 20.5 cm
Hence, the range, in centimetres (cm), of the following lengths is 20.5 cm
To learn more about range
https://brainly.com/question/29794774
#SPJ1
HELP PLSSSSSS!!! answer all pls

Answers
Answer:
See below.
Step-by-step explanation:
STEP 1: If you write the given terms all with denominators of 16, they are 28/16, 25/16, 22/16, 19/16, __, ____, ____, 7/16, 4/16.
STEP 2: The terms decrease by 3/16 for each step.
RULE: Term 1 = 7/4 and term (n + 1) = term 'n' - 3/16
The operation for increasing by the same amount every step is addition.
The operation for decreasing by the same amount every step is subtraction.
STEP 3: The rule is that the terms decrease by 3/16 at each step.
So the next 3 terms after 19/16 will be 16/16, 13/16, and 10/16.
Reformat them and you have 1, 13/16, 5/8.
So now the completed sequence is 1&3/4, 1&9/16, 1&3/8, 1&3/16, 1, 13/16, 5/8, 7/16, 1/4.
A. Are the expressions 3(m - 2) + 2(m - 2) and 5(m - 2) equivalent expressions? B. In two or more complete sentences, justify your answer to A.
Answers
A. Yes, the two expressions in discuss as given in the task content are; equivalent expressions.
B. The two expressions when simplified to the fewest terms is; 5m - 10. Hence, the two expressions are equivalent expressions.
Are the two expressions given equivalent expressions?It follows from the task content that the two expressions given are to be compared and determined if they are equivalent expressions.
A. By evaluation; using the Distributive property; we have;
3(m - 2) + 2(m - 2) = 3m - 6 + 2m - 4 = 5m - 10.
Also; 5(m - 2) = 5m - 10.
Therefore, the two expressions are equivalent.
B. Since both expressions given can be written in fewest terms as; 5m - 10, the expressions are equivalent. Hence, the two expressions are said to be equivalent expressions.
Read more on equivalent expressions;
https://brainly.com/question/24734894
#SPJ1
Sue and Pam are sisters, but they live far from each other. They both
want a garden at their respective homes, and they decide they want to
build identical flower gardens that are in the shape of a triangle.
They spend a lot of time emailing and talking on the phone, trying to
figure out how to make these triangular gardens exactly the same.
● Sue suggests that they each make their gardens with brick walls
outlining the gardens, and they should make sure all three angles
of the two triangles are the same: 30, 60, and 90. Sue asserts
that this will make their gardens congruent.
●
1
Pam likes the idea of the wall, but instead she thinks that they
should make their triangles equal by making one wall 7 feet long
with a 30 angle attached to it. Sue says the other two walls
•
will match up to make a triangle, and that their triangles will
be equal.
I
The two women can't agree on the best method. They hire you to help
them with the design.
•
Determine if either of their methods will create congruent
triangular gardens. Use your congruent triangle theorems, like
SSS, ASA, SAS, to decide.
. If you don't think that a method will work, you must explain why
the method will not work.
How do you think Sue and Pam should create congruent triangular
gardens?

Answers
On solving the provided question we can say that so SAS, the are congruent triangles
What is triangle?A triangle is a polygon since it has three sides and three vertices. It is one of the basic geometric shapes. The name given to a triangle containing the vertices A, B, and C is Triangle ABC. A unique plane and triangle in Euclidean geometry are discovered when the three points are not collinear. Three sides and three corners define a triangle as a polygon. The triangle's corners are defined as the locations where the three sides converge. 180 degrees is the result of multiplying three triangle angles.
here,
we have to triangles
with angles as 30,60,90 and 60,60,90 respectively
and 2 sides of 7 cm each.
so SAS, the are congruent triangles
To know more about triangle visit:
brainly.com/question/2773823
#SPJ1
A marine biologist measured one dish that was 1 1/4 of a foot and a second fish that was 3/4 of a foot long. How much longer was the first fish
Answers
Answer:
1/3 foot longer
Step-by-step explanation:
2/3-1/3=1/3
7 + 8/5-2
Could someone help me with this?
Answers
Answer:
hope it's helpful for you

State the Limits Rule and explain what it means
Answers
Answer:
The limit of a sum is equal to the sum of the limits.
Step-by-step explanation:
The limits of a constant times a function is equal to the constant times the limit of the function.
a) angle of line of From a point O in the school compound, Adeolu is 100 m away on a bearing N 35° E and Ibrahim is 80 m away on a bearing S 55° E. (a) How far apart are both boys? (b) (c) What is the bearing of Adeolu from point O, in three-figure bearings? What is the bearing of Ibrahim from point O, in three figure bearings? A boy walks 5 km due North and then 4 km due East. (a) Find the bearing of his current posi- tion from the starting point. (b) How far is the boy now from the start- ing point? A boy runs 200 m on a bearing of 230°.
Answers
a) Angle of line of sightFrom a point O in the school compound, Adeolu is 100 m away on a bearing N 35° E and Ibrahim is 80 m away on a bearing S 55° E. (a) How far apart are both boys? (b) (c) What is the bearing of Adeolu from point O, in three-figure bearings? What is the bearing of Ibrahim from point O, in three-figure bearings?The angle of the line of sight of Adeolu from the point O is given by:α = 90 - 35α = 55°.The angle of the line of sight of Ibrahim from the point O is given by:β = 90 - 55β = 35°.a) By using the Sine Rule, we can determine the distance between Adeolu and Ibrahim as follows:$
\frac{100}{sin55^{\circ}} = \frac{80}{sin35^{\circ}
100 sin 35° = 80 sin 55°=57.73 mT
herefore, both boys are 57.73 m apart. b) The bearing of Adeolu from the point O can be determined as follows:OAN is a right-angled triangle with α = 55° and OA = 100. Therefore, the sine function is used to determine the side opposite the angle in order to determine AN.
Thus:$$sin55^{\circ} = \frac{AN}{100}$$AN = 80.71 m.
To find the bearing, OAD is used as a reference angle. Since α = 55°, the bearing is 055°.
Therefore, the bearing of Adeolu from the point O is N55°E. c) Similarly, the bearing of Ibrahim from the point O can be determined as follows:OBS is a right-angled triangle with β = 35° and OB = 80. Therefore, the sine function is used to determine the side opposite the angle in order to determine BS.
Thus:$$sin35^{\circ} = \frac{BS}{80}$$BS = 46.40 m.
To find the bearing, OCD is used as a reference angle. Since β = 35°, the bearing is 035°.Therefore, the bearing of Ibrahim from the point O is S35°E. A boy walks 5 km due North and then 4 km due East. (a) Find the bearing of his current posi- tion from the starting point.
(b) How far is the boy now from the start- ing point?The boy's position is 5 km North and 4 km East from his starting position. The Pythagorean Theorem is used to determine the distance between the two points, which are joined to form a right-angled triangle. Thus
:$$c^2 = a^2 + b^2$$
where c is the hypotenuse, and a and b are the other two sides of the triangle. Therefore, the distance between the starting position and the boy's current position is:$$
c^2 = 5^2 + 4^2$$$$c^2 = 25 + 16$$$$c^2 = 41$$$$c = \sqrt{41} = 6.4 km$$
Therefore, the boy is 6.4 km from his starting point. (a) The bearing of the boy's current position from the starting point is given by the tangent function.
Thus:$$\tan{\theta} = \frac{opposite}{adjacent}$$$$\tan{\theta} = \frac{5}{4}$$$$\theta = \tan^{-1}{\left(\frac{5}{4}\right)}$$$$\theta = 51.34^{\circ}$$
Therefore, the bearing of the boy's current position from the starting point is N51°E.
For such more question on triangle
https://brainly.com/question/1058720
#SPJ8
Express the area of the entire rectangle.
Your answer should be a polynomial in standard form.

Answers
Answer:
x^2 + 12x + 27
Step-by-step explanation:
x^2 + 9x + 3x + 27 =
= x^2 + 12x + 27
Tina pet sits to earn extra money. She charges a flat service fee of $20, plus $15 per day. If one of her customers spent less than $125, which of the following inequalities could be used to solve for x, the number of days the customer paid for pet sitting?
Answers
Therefore, **x < 7** is the inequality that may be utilized to find x
What is inequality?A mathematical statement known as an inequality compares two expressions using an inequality sign, such as (less than), > (greater than), or (less than or equal to).
For instance, the inequality x + 2 5 signifies that "x + 2 is less than 5".
Let x represent how many days the client paid for pet sitting.
$15 per day plus a $20 fixed service fee equals the total cost of pet sitting.
We are aware that the customer's purchase was under $125. Consequently, we can write:
20 + 15x < 125
Putting this disparity simply:
15x < 105
x < 7
To know more about inequality visit:
brainly.com/question/11536194
#SPJ1
plz help me .........

Answers
Answer:
216 inches
Step-by-step explanation:
72+72+36+36=216
2c+7n+z=y solve for c
Answers
In order to solve for c we just have to remember one simple rule: what we do in one side of the equal "=" we should do it in the other side.
In this case:
2c + 7n + z = y
↓ substracting z both sides
2c + 7n + z - z = y - z
2c + 7n + 0 = y - z
2c + 7n = y - z
↓ substracting 7n both sides
2c + 7n - 7n = y - z - 7n
2c + 0 = y - z - 7n
2c = y - z - 7n
↓ dividing by 2 both sides
\(\begin{gathered} \frac{2c}{2}=\frac{y-z-7n}{2} \\ c=\frac{y-z-7n}{2} \end{gathered}\)Then, we have the answer:
\(c=\frac{y-z-7n}{2}\)