If your breakfast costs $12 and you are
charged 9% sales tax, what is the total
cost of your meal?
Answers
Answer:
find 9% of 12
12 times 9 divided by 100
108/100
$1.08
12+1.08
Your mean costs $13.08
-Have a nice meal!

Related Questions
Solve the differential equation
yy'ex' = x – 1; y (2) = 0 O y2 = In(x2 -x/2 +1) O y2 = ln(x^2 – 2x + 1) O y^2 = ln(x2 – 2x) + C O y^2 = ln(x2 – 2x)
Answers
The solution to the differential equation is given by the equation arctan(x) + arctan(y) - ln|x²+y²+1| = C.
The differential equation is given as:
x(1+y²)dx-y(1+x²)dy=0
To solve this differential equation, we can start by rearranging the terms and separating the variables. We can start by dividing both sides by x(1+y²), which gives:
dx/(1+y²) - y(1+x²)/(x(1+y²)) dy = 0
Next, we can integrate both sides of the equation. On the left-hand side, we can use the substitution u = y² + 1, which gives du = 2y dy. The equation then becomes:
∫dx/(1+y²) - ∫(1+x²)/x du = C
where C is the constant of integration.
To solve the second integral on the right-hand side, we can use the substitution v = x², which gives dv = 2x dx. The equation then becomes:
∫dx/(1+y²) - ∫(1+v)/v dv = C
To solve the first integral, we can use the substitution y = tanθ, which gives dy = sec²θ dθ. The equation then becomes:
∫dx/cos²θ - ∫(1+v)/v dv = C
We can simplify the first integral using the trigonometric identity sec²θ = 1 + tan²θ. The equation then becomes:
∫dx/(1+ tan²θ) - ∫(1+v)/v dv = C
The first integral can be evaluated using the substitution x = tanφ, which gives dx = sec²φ dφ. The equation then becomes:
∫sec²φ dφ/(1+tan²θ) - ∫(1+v)/v dv = C
Simplifying the first integral using the identity sec²φ = 1 + tan²φ, the equation becomes:
∫(1+tan²θ) dθ/(1+tan²θ) - ∫(1+v)/v dv = C
The first integral simplifies to ∫dθ, which is just θ + K, where K is another constant of integration. Substituting back the variables, we have:
arctan(x) + arctan(y) - ln|v| = C
where v = x² and C = K - ln|D|, where D is a constant of integration.
Finally, we can substitute back the variables u = y² + 1 and v = x² to obtain the solution to the differential equation:
arctan(x) + arctan(y) - ln|x²+y²+1| = C
To know more about differential equation here
https://brainly.com/question/30074964
#SPJ4
Complete Question:
Solve the differential equation:
x(1+y²)dx-y(1+x²)dy=0
Solve the equation
3/2x - 2 > 7
Answers
You can multiply each side of equation by the denominator to eliminate the fraction.
Work:

karen purchased a DVD player on sale. the original price was $175.80. the sale price was 153.67 what is the first step in finding the percent markdown? find the percent markdown.
Answers
The percent markdown is 22.58% for the given DVD player.
What is the percentage?The percentage is defined as a ratio expressed as a fraction of 100.
We can determine the value of the percent markdown by the following formula,
percentage decrease = (initial value - reduced value) / initial value × 100%
As per the given question, we have
initial value = $175.80, and reduced value = $153.67
Substitute the values in the above formula, and we get
percent markdown = (175.80 - 153.67) / 175.80 × 100%
percent markdown = (22.13) / 175.80 × 100%
percent markdown = 0.1258 × 100%
Apply the multiplication operation, and we get
percent markdown = 12.58 %
Thus, the percentage decrease of the given item would be 12.58%.
Learn more about the percentages here:
brainly.com/question/24159063
#SPJ1
helpppppp pleaseeeee

Answers
Answer:
\(x^2+\left(b^3-3bc\right)x+c^3=0\)
\(\alpha = 1 \quad \textsf{and} \quad \beta=2\)
\(b=-3\)
Step-by-step explanation:
If α and β are roots of x² + bx + c = 0 then the equation must be:
\((x -\alpha)(x - \beta) = 0\)
Expanding we get:
\(x^2-\beta x - \alpha x + \alpha \beta = 0\)
\(x^2-(\alpha +\beta ) x + \alpha \beta = 0\)
Equating the coefficients we get:
\(\alpha + \beta=-b\)
\(\alpha \cdot \beta=c\)
For an equation with the roots α³ and β³, the sum of the roots can be rewritten in terms of (α + β) and (α·β) using the Sum of Cubes formula, and the Square of Binomials formula:
\(\begin{aligned}\alpha^3+\beta^3&=(\alpha + \beta)(\alpha^2-\alpha\beta+\beta^2)\\&=(\alpha + \beta)(\alpha^2+2\alpha\beta+\beta^2-3\alpha\beta)\\&=(\alpha + \beta)((\alpha+\beta)^2-3\alpha\beta))\end{aligned}\)
Substitute in the expressions for (α + β) and αβ to find the sum of the roots α³ and β³ in terms of b and c:
\(\begin{aligned}\alpha^3+\beta^3&=(\alpha + \beta)((\alpha+\beta)^2-3\alpha\beta))\\&=(-b)((-b)^2-3c))\\&=-b(b^2-3c)\\&=-b^3+3bc\end{aligned}\)
The product of the roots α³ and β³ in terms of c is:
\(\alpha \cdot \beta = c\)
\((\alpha \cdot \beta)^3 = c^3\)
\(\alpha^3 \cdot \beta^3=c^3\)
For a quadratic equation in the form x² + bx + c = 0:
The sum of the roots is equal to -b.The product of the roots is equal to c.So for x² + bx + c = 0 with roots α³ and β³:
\(x^2-(\alpha^3 + \beta^3)x+(\alpha^3 \cdot \beta^3)=0\)
\(x^2-\left(-b^3-3bc\right)x+c^3=0\)
\(x^2+\left(b^3-3bc\right)x+c^3=0\)
Therefore, the equation with the roots α³ and β³ is:
\(\boxed{x^2+\left(b^3-3bc\right)x+c^3=0}\)
Substitute the given value of c = 2:
\(x^2+\left(b^3-3b(2)\right)x+2^3=0\)
\(x^2+\left(b^3-6b\right)x+8=0\)
If b³ - 6b + 9 = 0, then (b³ - 6b) = -9.
Substitute this into the equation:
\(x^2-9x+8=0\)
Factor:
\((x-1)(x-8)=0\)
Therefore, the roots of the equation with the roots α³ and β³ are 1 and 8, so the values of α and β are:
\(\alpha^3 =1 \implies \alpha = 1\)
\(\beta^3=8 \implies \beta=2\)
To find the real roots of b³ - 6b + 9 = 0, substitute the found values of α and β into the expression for b:
\(b=-(\alpha + \beta)\)
\(b=-(1+2)\)
\(b=-3\)
Therefore, the real root of b³ - 6b + 9 = 0 is b = -3.
We can confirm this by substituting b = -3 into the equation:
\(\begin{aligned}(-3)^3-6(-3)+9&=-27+18+9\\&=-9+9\\&=0\end{aligned}\)
1. What is the slope of the line that passes through the points (26, 7) and (-39, 12)?
Answers
Answer:
m = 68/5.
Step-by-step explanation:
points (26, 7) and (-39, 12)
Gradient (m) =
\( = \frac{y2 - y1}{x2 - x1} \\ = \frac{ - 39 - 26}{12 - 7} \\ = \frac{68}{5} \)
therefore the gradient (m) = 68/5.
Consuelo deposited an amount of money in a savings account that earned 6. 3% simple interest. After 20 years , she had earned $5’922 in interest. What was her initial deposit
Answers
Consuelo deposited an amount of money in a savings account that earned 6. 3% simple interest. After 20 years , she had earned $5’922 in interest then the initial deposit was $4700
Use the simple interest formula
I = P r t
where I = simple interest
P = principal
r= rate of interest
t= number of years
5922=Px6.3%x20
5922=Px1.26
P=5922/1.26
P=4700
learn more about of amount here
https://brainly.com/question/27054498
#SPJ4
Solve for b
SOLVE ASAP!!

Answers
Answer:
Step-by-step explanation:
<A and <B are alternate interior angles. That means they are in the interior of the parallel lines and they are on opposite sides of the transversal.
When that happens <A = <B
8x + 78 = 2x + 114 Subtract 2x from both sides.
8x - 2x + 78 = 2x - 2x + 114 Combine
6x + 78 = 114 Subtract 78 from both sides
6x + 78 - 78 = 114 - 78
6x = 36 Divide by 6
6x/6 = 36/6
x = 6
I think you are asked for B
<B = 2x + 114
<B = 2*6 + 114
<B = 12 + 114
<B = 126
Given f(x)=x*-x³-6x², for what values of x will f(x) > 0?
Answers
The values of x will f(x) > 0 for x < 0, and f(x) < 0 for -6 < x < 0 and x > -6.
To determine the values of x for which f(x) > 0, we need to find the intervals where the function is positive. Let's analyze the function f(x) = x*-x³-6x².
First, let's factor out an x from the expression to simplify it: f(x) = x(-x² - 6x).
Now, we can observe that if x = 0, the entire expression becomes 0, so f(x) = 0.
Next, we analyze the signs of the factors:
1. For x < 0, both x and (-x² - 6x) are negative, resulting in a positive product. Hence, f(x) > 0 in this range.
2. For -6 < x < 0, x is negative, but (-x² - 6x) is positive, resulting in a negative product. Therefore, f(x) < 0 in this range.
3. For x > -6, both x and (-x² - 6x) are positive, resulting in a negative product. Thus, f(x) < 0 in this range.
For such more questions on values
https://brainly.com/question/843074
#SPJ8
\( {7}^{2x + 3} = 1\)
Answers
Answer:
x = -3/2
Step-by-step explanation:
7⁰ = 1 (anything to the power of 0 equals 1)
7²ˣ ⁺ ³ = 7⁰
Since the bases are the same, you 'forget' about the bases and then you solve for x.
2x + 3 = 0
2x = -3
x = -3/2
for exercise, mae jogs miles then walks an additional to cool down. if her jogging speed is miles per hour faster than her walking speed and her total exercise time is , what is her walking speed?
Answers
Mae's walking speed is 10 miles per hour. This is calculated by considering the given information.
Let's assume Mae's walking speed is represented by the variable "x" (in miles per hour). According to the given information, her jogging speed would then be "x + 12.5" miles per hour.
To calculate Mae's exercise time, we can use the formula: time = distance / speed.
Mae jogs 27 miles at a speed of "x + 12.5" miles per hour, so her jogging time can be calculated as:
jogging time = 27 / (x + 12.5)
Mae walks an additional 3 miles at a speed of "x" miles per hour, so her walking time can be calculated as:
walking time = 3 / x
The total exercise time is given as 3 hours. Therefore, we can set up the equation:
jogging time + walking time = 3
Substituting the calculated values, we get:
27 / (x + 12.5) + 3 / x = 3
To solve this equation, we can start by multiplying all terms by x(x + 12.5) to eliminate the denominators:
27x + 27 * 12.5 + 3(x + 12.5) = 3x(x + 12.5)
Simplifying the equation:
\(27x + 337.5 + 3x + 37.5 = 3x^2 + 37.5x\)
Combining like terms:
\(30x + 375 = 3x^2 + 37.5x\)
Rearranging the terms to set the equation equal to zero:
\(3x^2 + 7.5x - 375 = 0\)
To solve this quadratic equation, we can use the quadratic formula:
x = (-b ± √(\(b^2\) - 4ac)) / (2a)
In this case, a = 3, b = 7.5, and c = -375. Substituting these values into the quadratic formula:
x = (-7.5 ± √(\(7.5^2\) - 4 * 3 * -375)) / (2 * 3)
x = (-7.5 ± √(56.25 + 4500)) / 6
x = (-7.5 ± √(4556.25)) / 6
Calculating the square root:
x = (-7.5 ± 67.5) / 6
Simplifying further:
x = (60 / 6) or x = (-75 / 6)
Since Mae's walking speed cannot be negative, the solution is x = 10.
Therefore, Mae's walking speed is 10 miles per hour.
Learn more about quadratic equation here:
https://brainly.com/question/1214333
#SPJ11
The complete question is:
For exercise, Mae jogs 27 miles then walks an additional 3 miles to cool down. If her jogging speed is 12.5 miles per hour faster than her walking speed and her total exercise time is 3 hours, what is her walking speed? The athlete's walking speed is
How many solutions are there to the equation x 1 +x 2 +⋯+x 5=94 where x i∈N and x i ≤33 for all i ?
Answers
Using the stars and bars technique, the number of solutions to the equation \(x_1 + x_2 + \ldots + x_5 = 94\) with \(x_i \in \mathbb{N}\) and \(x_i \leq 33\) is 75,287,520.
To find the number of solutions to the equation \(x_1 + x_2 + \ldots + x_5 = 94\) with the given conditions \(x_i \in \mathbb{N}\) and \(x_i \leq 33\) for all \(i\), we can use a technique called stars and bars.
Let's introduce five "stars" to represent the sum \(94\). Now, we need to distribute these stars among five "bars" such that each bar represents one of the variables \(x_1, x_2, \ldots, x_5\). The stars placed before each bar will correspond to the value of the respective variable.
To ensure that \(x_i \leq 33\) for all \(i\), we can introduce five "extra" stars and place them after the last bar. These extra stars guarantee that each variable will be less than or equal to 33.
Now, we have \(94 + 5 = 99\) stars and \(5\) bars, which we can arrange in \({99 \choose 5}\) ways.
Therefore, the number of solutions to the equation is given by:
\({99 \choose 5} = \frac{99!}{5!(99-5)!}\)
Evaluating this expression, we get:
\({99 \choose 5} = \frac{99!}{5!94!} = 75,287,520\)
So, there are 75,287,520 solutions to the equation \(x_1 + x_2 + \ldots + x_5 = 94\) under the given conditions.
To learn more about expression click here brainly.com/question/29696241
#SPJ11
What is the square root of 450 divided by 5?
Answers
Answer:
The square root of 450 is irrational, meaning it never ends. As an estemate though the answer is 4.24
Step-by-step explanation:
¾ (x - 13) = -2 (9 + x)
Answers
1) The way to tackle this expression is to apply the Distributive Property, a.k.a by the acronym FOIL
2) So, we can write down the following development:
\(\begin{gathered} \frac{3}{4}(x-13)=-2(9+x) \\ \frac{3}{4}x-\frac{39}{4}=-18-2x \\ \frac{3}{4}x+2x=-18+\frac{39}{4} \\ \frac{3}{4}x+\frac{8}{4}x=-\frac{72}{4}+\frac{39}{4} \\ \frac{11}{4}x=-\frac{33}{4} \\ 4\times\frac{11}{4}x=-\frac{33}{4}\times4 \\ 11x=-33 \\ \frac{11x}{11}=-\frac{33}{11} \\ x=-3 \end{gathered}\)Note that we have distributed the factors over the parentheses and then we rewrote those whole numbers as fractions.
Thus, the answer is x=-3
You perform an hypothesis test and the null hypothesis was not rejected at an alpha level of 0.05. You want to perform the same test using an alpha of 0.25. What will be your conclusion? a. Fail to reject the null hypothesis b. Accept the alternative hypothesis c. No conclusion can be made
d. Reject the null hypothesis e. Reject the alternative hypothesis
Answers
The correct answer is a. Fail to reject the null hypothesis.
Explanation:
When performing a hypothesis test, the alpha level is the probability of rejecting the null hypothesis when it is actually true. A lower alpha level, such as 0.05, means that there is a smaller chance of making a Type I error (rejecting the null hypothesis when it is actually true). If the null hypothesis was not rejected at an alpha level of 0.05, it means that there was not enough evidence to support the alternative hypothesis.
When the alpha level is increased to 0.25, the probability of making a Type I error increases, but it does not change the conclusion of the test. The null hypothesis will still fail to be rejected because there is not enough evidence to support the alternative hypothesis.
Learn more about null hypothesis:
https://brainly.in/question/3231387#:~:text=Expert%2DVerified%20Answer&text=Statistical%20hypothesis%20testing%20employs%20null,or%20no%20association%20between%20variables.
#SPJ11
Cual es el area de un semicírculo que se diámetro es 14
Answers
The area of a circle is given by:
\(A_C=\frac{1}{4}\cdot\pi\cdot d^2.\)Where π ≅ 3.14 and d is the diameter of the circle.
Now, a semi-circle is a half of a circle, so its area is half of the area of the complete circle:
\(A_{SC}=\frac{1}{2}\cdot A_C=\frac{1}{2}\cdot(\frac{1}{4}\cdot\pi\cdot d^2)=\frac{1}{8}\cdot\pi\cdot d^2\text{.}\)Replacing the value d = 14 in the last formula, we get:
\(A_{SC}=\frac{1}{8}\cdot\pi\cdot(14units)^2=24.5\cdot\pi\cdot units^2\cong76.97units^2.\)Answer
The area of a semicircle with a diameter d =14 is approximately 76.97 units square.
EXTRA POINTS The amount of people diagnosed is 3,131,953 and the amount of deaths is 132,056 what is the percentage of people who die from the disease?
Answers
2.3%
divide the infected number by the deaths. Then move the decimal points to the left.
Answer:
2.3%
divide the infected number by the deaths. Then move the decimal points to the left.
Step-by-step explanation:
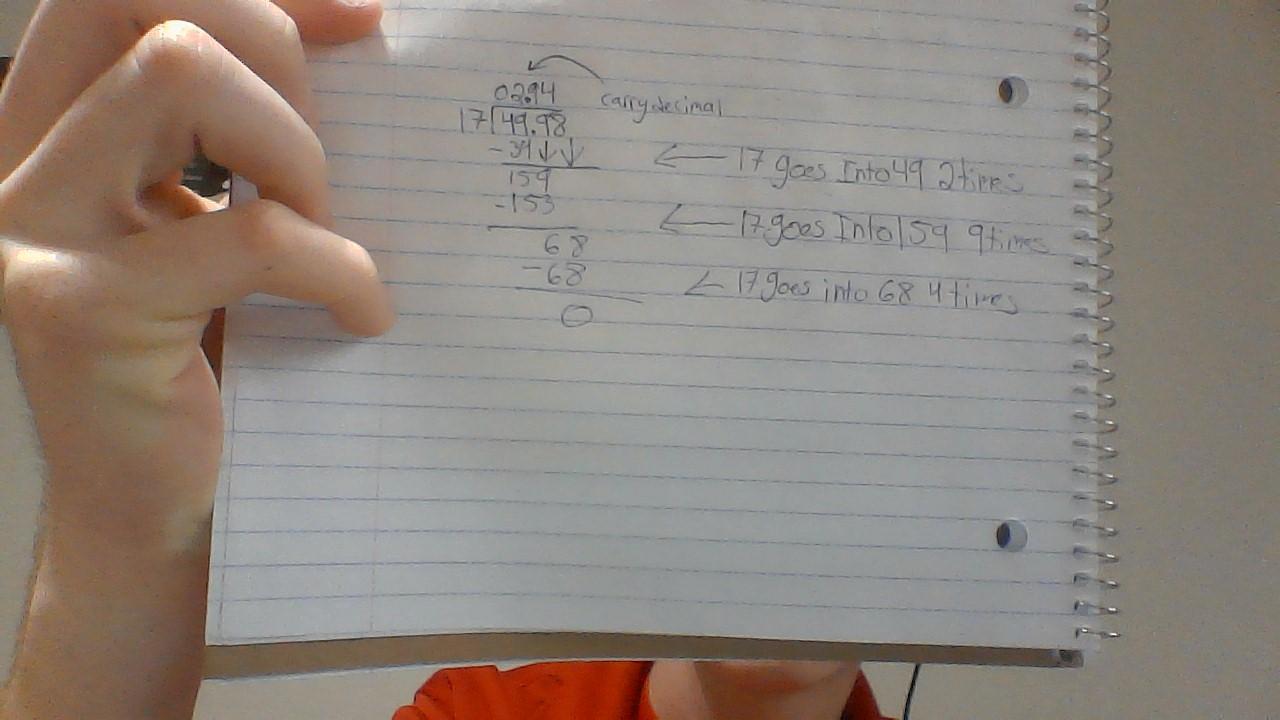
49.98 ÷ 17 = ? (show ur work)
Answers
Answer:
2.94
Step-by-step explanation:
In the picture below
ASAP! FIND THE AREA OF THE SECTOR

Answers
Answer:
probably B
Step-by-step explanation:
Using the formula pi*r^2, we plug in our values
pi*49=49pi mi^2
but, we still have one more step, as we are calculating for three quarters of a circle, not a full circle.
To find the area for 3/4 of a circle, we just multiply 3/4 by the area of the circle
49pi*3/4=147pi/4
A quick way (though not always accurate) to guess the answer in a multiple choice like this is to see that someone might find the area of the full circle as their final answer, not multiplying by 3/4, so there's a good chance that 49pi mi^2 would be an answer in the multiple choice. since we know that there is a correct answer that is exactly 3/4 of that answer, we can take the ratios of the answers and check if any of them equal 3/4. indeed, after checking a bit, answer B divided by answer A equals 3/4 exactly, and no other answer combination equals 3/4 (D/B is about equal to 4/5). So, we can guess that B is the answer.
Still better to actually do the problem though
13 POINTS FOR THIS GUYS PlEASE HELP

Answers
Answer:
I'm pretty sure
dependent: total video games
independent: number of months
A square that measures one yard on each side will have an answer of square yards
Answers
Length x width is the formula.
Hope this helps
describe how the function and its graph would chjange if the tire's radius was 24 inches instead of 25 cm
Answers
If the tire's radius is changed from 25 cm to 24 inches, the function representing the tire's rotation would require adjustment, incorporating the new radius in its equation. The graph would also change, displaying a slightly different shape and scale due to the alteration in units and resulting adjustments in the function.
When the tire's radius is changed from 25 cm to 24 inches, the function representing the tire's rotation would need to be modified. The original function, which might have been something like f(x) = 2π(25x), where x represents the number of rotations, would now need to incorporate the new radius. Using the conversion factor of 1 inch = 2.54 cm, the adjusted function would become f(x) = 2π(24x/2.54).
The graph representing the function would also be affected by this change. With the new radius, the graph would display a slightly different shape and scale compared to the original one. The x-axis, which represents the number of rotations, would remain the same, but the y-axis, representing the distance traveled, would be altered due to the change in units. The graph's curvature and overall appearance might be slightly different, reflecting the adjustment made to the function.
Learn more about radius here: https://brainly.com/question/31884051
#SPJ11
Solve the system using substitution (1 point)
x + y = 8
y = 3x
(A). (4, 12)
(B). (2, 6)
(C). (1/2, 3/2)
(D). (-4, -12)
Answers
The solution to the system is x = 2 and y = 6, represented as the ordered pair (2, 6). This corresponds to option (B) in the answer choices.
To solve the system using substitution, we'll substitute the value of one variable from one equation into the other equation and solve for the remaining variable.
Given the system:
x + y = 8
y = 3x
Substituting the value of y from the second equation into the first equation, we have:
x + (3x) = 8
4x = 8
x = 2
Now, substitute the value of x into the second equation to solve for y:
y = 3(2)
y = 6
Therefore, the solution to the system is (2, 6). Option (B) is the correct answer.
To know more about variable click here
brainly.com/question/2466865
#SPJ11
Please answer this I give brainliest! :-) No responding fake answers, will be reported to the service:
It costs $35 to join a gym. The monthly fee is $25. Write and graph an equation in 2 variables that represent the total cost of a gym membership. Let m represent the number of months and c represent the total cost of the gym membership.
Answers
Answer:
c=35 + 25m
Step-by-step explanation:
Sorry, that's all I got
The urface area of a cylinder i 24π m². The ditance around the bae of the cylinder i 3π meter and the diameter of a bae of the cylinder i 4 meter. What i the height of the cylinder? Enter your anwer, a a implified fraction, in the box
Answers
After solving, the height of the cylinder is 6 meters.
The surface area of a cylinder is 24π m².
The distance around the base of the cylinder is 3π meter.
The diameter of a base of the cylinder is 4 meter.
Now the radius of the cylinder = diameter/2
The radius of the cylinder = 4/2
The radius of the cylinder = 2 meter.
The formula of surface area of cylinder:
S = 2πrh
From the question:
2πrh = 24π
Now putting the value of r
2π × 2 × h = 24π
4πh = 24π
Divide by 4π on both side, we get
h = 6
To learn more about surface area of cylinder link is here
brainly.com/question/22074027
#SPJ4
The complete question is:
The surface area of a cylinder is 24π m². The distance around the base of the cylinder is 3π meter and the diameter of a base of the cylinder is 4 meter. What is the height of the cylinder? Enter your answer, in a simplified fraction, in the box.
What is the slope of the line passing through the points (-1, 7) and (3, 4)?
Answers
Answer:
-3/4
Step-by-step explanation:
The formula for slope is [ y2-y1/x2-x1 ].
4-7/3-(-1)
-3/4
Best of Luck!
Answer:
The slope is -3/4x.
Step-by-step explanation:
Slope = \(\frac{y_{2} -y_1}{x_{2} -x_1}\)
\(\frac{4-7}{3--1}\)
\(\frac{4-7}{3+1}\)
\(\frac{-3}{4}\)
\(-\frac{3}{4}\)
What is the value of X?

Answers
Answer:
x=12°
Step-by-step explanation:
180 - 90 = 4x - 2° + 3x + 8 °
90°= 7x + 6
90° - 6 = 7x
7x = 84
x= 84/7
x = 12
Describe the shape of the distribution.
A. It is symmetric.
B. It is uniform.
C. It is bimodal.
D. It is skewed.

Answers
What is The Sum of the solutions of the two equations Below?
8x=12
2y+10=22
A. 2 2/5
B.7 1/2
C.9
D.10
E.17 1/2
Answers
Answer:
B. 7 1/2
Step-by-step explanation:
8x=12
x = 1.5
2y+10=22
2y = 12
y = 6
1.5 + 6 = 7.5
So, the sum of the solutions of the two equations is
B. 7 1/2
Answer:
Step-by-step explanation:
firstly we solve 8x=12 we divide both sides by 8 since 8 is the coefficient of x so we are trying to find x that is 8x divided by 8 which is x =12 divided by 8 which is 1.5 which means x=1.5 then we solve the second one 2y+10=22 we collect like terms which means 2y=22-10 as you should know the 10 changes to negative when crossed over to the other side so then 2y=12 is the answer then we divide both sides by the coefficient of y which is 2 so 2y divided by 2 =y 12 divided by 2 = 6 so y=6 then we add both of them together x=1.5+(y=6) so add 1.5 and 6 together answer is 7.5 or 7 1/2
Due soon FOR 20 POINTS AND BRAINLY
which transformation represents a dilation centered at the origin
A). (x,y) → (x,3y)
B). (x,y) → (x,y 0.25x,y)
C). (x,y) → (2x,-4y)
D). (x,y) →(0.75x,0.75y)
Answers
The transformation (x,y) →(0.75x,0.75y) represents a dilation centered at the origin. which is the correct answer would be an option (D).
What is a transformation?A point is transformed when it is moved from where it was originally to a new location. Translation, rotation, reflection, and dilation are examples of different transformations.
On the coordinate plane, you may dilate figures. The origin is frequently utilized as the center of dilatation. If you are distorting a figure centered at the origin, you may find the points in the image by multiplying the coordinates of the points in the preimage by the scale factor.
As per the given option, we can see the scale factor i.e. 0.75 is multiplying the coordinates of the points (x, y) in option (D).
Thus, the transformation (x,y) →(0.75x,0.75y) represents a dilation centered at the origin.
To learn more about the transformations click here :
https://brainly.com/question/28029674
#SPJ1
There is a triangular parking lot at the local mall. The second angle of the triangular parking lot is six more than twice as large as the first angle. The third angle is equal to the sum of the other two angles. What are the measures of the three angles?
Answers
Answer:
The measure of the three angles are;
The first angle is 62°
The second angle is 28°
The third angle is 90°
Step-by-step explanation:
The given information are;
The shape of the parking lot = Triangular
Let the angles of the triangle be given as follows
First angle = A
Second angle = B
Third angle = C
The given triangle interior angle dimensions are;
A = 6 + 2× B
C = A + B
However, we have;
A + B + C = 180° (Angle sum property for a triangle)
Therefore;
A + B + C = 180° gives;
C + C = 180° (Transitive property)
2·C = 180°
C = 180°/2 = 90°
C = 90°
However, C = A + B therefore;
90° = A + B and, A = 6 + 2 × B, we get;
A + B = 90° (Symmetric property)
6 + 2× B + B = 90° (Substitution property)
6 + 3·B = 90°
3·B = 90° - 6° = 84°
B = 84°/3 = 28°
B = 28°
From, A = 6 + 2 × B, we have;
A = 6 + 2 × 28° = 62°
A = 62°
First angle = A = 62°
Second angle = B = 28°
Third angle = C = 90°
The measure of the three angles are;
First angle is 62°
Second angle is 28°
Third angle is 90°.