In JKL, J = 7.9 inches, K = 2 inches and L =9.8 inches. Find the measure of K to the nearest degree
Answers
Answer:
4
Step-by-step explanation:
Delta math
The measure of K to the nearest degree is 4°.
What is the laws of cosines?The law of cosines, commonly referred to as the cosine rule or the cosine formula, in trigonometry essentially connects the length of the triangle to the cosines of one of its angles. It claims that we can determine the length of the third side of a triangle if we know the length of the first two sides and the angle between them.
Given ΔJKL,
j = 7.9 inches, k = 2 inches, l = 9.8 inches
to find the measure of angle K,
we can calculate the angle by cosine law,
cosK = (j² + l² - k²)/(2.j.l)
cosK = (7.9² + 9.8² - 2²)/(2*7.9*9.8)
cosK = 154.45/154.81
K = cos⁻¹(0.99748)
K = 4.067⁰ ≈ 4°
Hence angle K is 4°.
Learn more about the laws of cosines;
https://brainly.com/question/17289163
#SPJ1
Related Questions
Steven has $1294.00 in his savings account. He makes a deposit of $100.00 , and for the next 4 weeks he withdraws $350.50 each week. What is his balance at the end of the 4 weeks?
- $108.00
- $8.00
$493.00
$1244.50
Answers
Answer:
-8$
Step-by-step explanation:
first, add 100 to 1,294
then multiply 350.50 by 4
and subtract them
Annette has 3 hours to spend training for an upcoming race. She completes her training by running full speed the distance of the race and walking back the same distance to cool down. If she runs at a speed of 9mph and walks back at a speed of 3mph , how long should she plan to spend walking back?
Answers
Answer:
Annette should plan to spend 2.25 hours walking back.
Step-by-step explanation:
To solve this problem, we can use the formula:
Time = Distance / Speed
Let's assume the distance of the race is D miles.
Annette spends her time running the distance of the race, which takes:
Time running = D / 9 hours
She then walks back the same distance, which we need to find the time for:
Time walking = D / 3 hours
Since Annette has a total of 3 hours for her training, the sum of the running time and walking time should equal 3 hours:
D / 9 + D / 3 = 3
To simplify the equation, we can multiply all terms by 9 to eliminate the denominators:
D + 3D = 27
Combining like terms:
4D = 27
Dividing both sides of the equation by 4:
D = 6.75
So, the distance of the race is 6.75 miles.
To find the time Annette should spend walking back, we substitute the distance into the time-walking formula:
Time walking = D / 3 = 6.75 / 3 = 2.25 hours
Therefore, Annette should plan to spend 2.25 hours walking back.
Evaluate the function f(x) at the given numbers (correct to six decimal places).
f(x) =
x2 − 2x
x2 − 4
,
x = 2.1, 2.05, 2.01, 2.001, 2.0001,
1.9, 1.95, 1.99, 1.999, 1.9999
x f(x)
2.1
0.512195
Correct: Your answer is correct.
2.05
0.5062
Incorrect: Your answer is incorrect.
2.01
0.5012
Incorrect: Your answer is incorrect.
2.001
0.5000
Incorrect: Your answer is incorrect.
2.0001
0.500012
Correct: Your answer is correct.
x f(x)
1.9
0.487179
Correct: Your answer is correct.
1.95
0.493670
Incorrect: Your answer is incorrect.
1.99
0.498746
Incorrect: Your answer is incorrect.
1.999
0.499874
Incorrect: Your answer is incorrect.
1.9999
0.499987
Correct: Your answer is correct.
Answers
Answer:
\(f(2.1) = 0.512195\)
\(f(2.05) = 0.506173\)
\(f(2.01)=0.501247\)
\(f(2.001) = 0.500125\)
\(f(2.0001) = 0.500012\)
\(f(1.9) = 0.487179\)
\(f(1.95) = 0.493671\)
\(f(1.99) = 0.498747\)
\(f(1.999) = 0.499875\)
\(f(1.9999) = 0.499987\)
Step-by-step explanation:
Given
\(f(x) = \frac{x^2 - 2x}{x^2 - 4}\)
Solve for f(x) for all given values of x
First, we need to simplify f(x)
\(f(x) = \frac{x^2 - 2x}{x^2 - 4}\)
\(f(x) = \frac{x(x - 2)}{x^2 - 2^2}\)
\(f(x) = \frac{x(x - 2)}{(x- 2)(x + 2)}\)
\(f(x) = \frac{x}{x + 2}\)
When \(x = 2.1\)
\(f(x) = \frac{x}{x + 2}\)
\(f(2.1) = \frac{2.1}{2.1 + 2}\)
\(f(2.1) = \frac{2.1}{4.1}\)
\(f(2.1) = 0.512195\)
When \(x = 2.05\)
\(f(x) = \frac{x}{x + 2}\)
\(f(2.05) = \frac{2.05}{2 + 2.05}\)
\(f(2.05) = \frac{2.05}{4.05}\)
\(f(2.05) = 0.506173\)
When \(x = 2.01\)
\(f(x) = \frac{x}{x + 2}\)
\(f(2.01)=\frac{2.01}{2.01 +2}\)
\(f(2.01)=\frac{2.01}{4.01}\)
\(f(2.01)=0.501247\)
When \(x = 2.001\)
\(f(x) = \frac{x}{x + 2}\)
\(f(2.001) = \frac{2.001}{2.001 +2}\)
\(f(2.001) = \frac{2.001}{4.001}\)
\(f(2.001) = 0.500125\)
When \(x = 2.0001\)
\(f(x) = \frac{x}{x + 2}\)
\(f(2.0001) = \frac{2.0001}{2.0001 + 2}\)
\(f(2.0001) = \frac{2.0001}{4.0001}\)
\(f(2.0001) = 0.500012\)
When \(x = 1.9\)
\(f(x) = \frac{x}{x + 2}\)
\(f(1.9) = \frac{1.9}{1.9 + 2}\)
\(f(1.9) = \frac{1.9}{3.9}\)
\(f(1.9) = 0.487179\)
When \(x = 1.95\)
\(f(x) = \frac{x}{x + 2}\)
\(f(1.95) = \frac{1.95}{1.95 + 2}\)
\(f(1.95) = \frac{1.95}{3.95}\)
\(f(1.95) = 0.493671\)
When \(x = 1.99\)
\(f(x) = \frac{x}{x + 2}\)
\(f(1.99) = \frac{1.99}{1.99 + 2}\)
\(f(1.99) = \frac{1.99}{3.99}\)
\(f(1.99) = 0.498747\)
\(f(x) = \frac{x}{x + 2}\)
When \(x = 1.999\)
\(f(x) = \frac{x}{x + 2}\)
\(f(1.999) = \frac{1.999}{1.999 + 2}\)
\(f(1.999) = \frac{1.999}{3.999}\)
\(f(1.999) = 0.499875\)
When x = 1.9999
\(f(x) = \frac{x}{x + 2}\)
\(f(1.9999) = \frac{1.9999}{1.9999 + 2}\)
\(f(1.9999) = \frac{1.9999}{3.9999}\)
\(f(1.9999) = 0.499987\)
Note that all values of f(x) are approximated to 6 decimal places
Evaluate ∫ y2dx + x dy along the following paths. (a) C = C1 is the line segment from (-13, -7) to (0, 6) (b) C = C2 is the arc of the parabola x = 36 - y2 from (-13, -7) to (0, 6).
Answers
a. Parameterize C₁ by
\((x(t),y(t)) = (1-t)(-13,-7) + t(0,6) = (-13+13t,-7+13t)\)
with 0 ≤ t ≤ 1. Then both dx = 13 dt and dy = 13 dt, so that the line integral along C₁ is
\(\displaystyle \int_C y^2\,dx + x\,dy = \int_0^1 (-7+13t)^2(13\, dt) + (-13+13t)(13\,dt)\)
\(\displaystyle \int_C y^2\,dx + x\,dy = 13 \int_0^1 (169t^2 - 169t + 36) \, dt\)
\(\displaystyle \int_C y^2\,dx + x\,dy = 13 \left(\frac{169}3-\frac{169}2+36\right) = \boxed{\frac{611}6}\)
b. Parameterize C₂ by
\((x(t),y(t)) = (36-t^2,t)\)
with -7 ≤ t ≤ 6. Then dx = -2t dt and dy = dt, so the line integral is
\(\displaystyle \int_C y^2\,dx + x\,dy = \int_{-7}^6 t^2(-2t\,dt) + (36-t^2)\,dt\)
\(\displaystyle \int_C y^2\,dx + x\,dy = \int_{-7}^6 (36-t^2-2t^3) \, dt\)
\(\displaystyle \int_C y^2\,dx + x\,dy = \left(36\cdot6-\frac{6^3}3-\frac{6^4}2\right) - \left(36\cdot(-7)-\frac{(-7)^3}3-\frac{(-7)^4}2\right) = \boxed{\frac{5005}6}\)
HELP I NEED THE ANSWER FAST “NO LINKS”

Answers
Answer:
a
Step-by-step explanation:
240
SOMEBODY HELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIEST
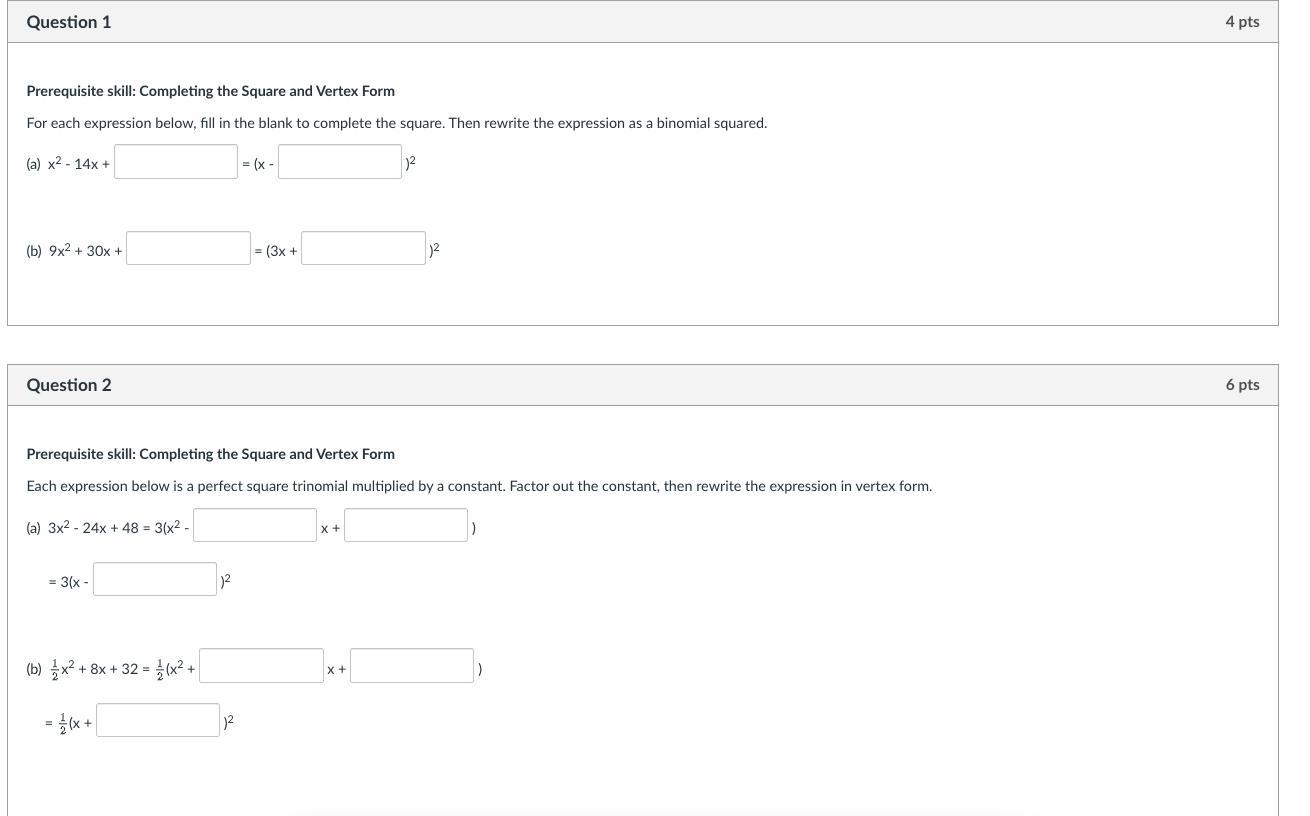
Answers
Answer:
\(\textsf{1.(a)} \quad x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
\(\textsf{1.(b)} \quad 9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\begin{aligned}\textsf{2.(a)}\quad3x^2-24x+48&=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\\&=3\left(x-\boxed{4}\right)^2\end{aligned}\)
\(\begin{aligned}\textsf{2.(b)}\quad \dfrac{1}{2}x^2+8x+32&=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\\&=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\end{aligned}\)
Step-by-step explanation:
Question 1(a) When completing the square for a quadratic equation in the form ax² + bx + c where the leading coefficient is one, we need to add the square of half the coefficient of the x-term:
\(x^2-14x+\left(\dfrac{-14}{2}\right)^2\)
\(x^2-14x+\left(-7\right)^2\)
\(x^2-14x+49\)
We have now created a perfect square trinomial in the form a² - 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Therefore:
\(a^2=x^2 \implies a=1\)
\(b^2=49=7^2\implies b = 7\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
(b) When completing the square for a quadratic equation where the leading coefficient is not one, we need to add the square of the coefficient of the x-term once it is halved and divided by the leading coefficient, and then multiply it by the leading coefficient:
\(9x^2 + 30x +9\left(\dfrac{30}{2 \cdot 9}\right)^2\)
\(9x^2 + 30x +9\left(\dfrac{5}{3}\right)^2\)
\(9x^2 + 30x +9 \cdot \dfrac{25}{9}\)
\(9x^2 + 30x +25\)
We have now created a perfect square trinomial in the form a² + 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 +2ab + b^2 = (a +b)^2}\)
Therefore:
\(a^2=9x^2 = (3x)^2 \implies a = 3x\)
\(b^2=25 = 5^2 \implies b = 5\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\hrulefill\)
Question 2(a) Factor out the leading coefficient 3 from the given expression:
\(3x^2-24x+48=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\)
We have now created a perfect square trinomial in the form a² - 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=3\left(x-\boxed{4}\right)^2\)
(a) Factor out the leading coefficient 1/2 from the given expression:
\(\dfrac{1}{2}x^2+8x+32=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\)
We have now created a perfect square trinomial in the form a² + 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2+2ab + b^2 = (a +b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\)
Step-by-step explanation:
Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
Max has 382 baseball cards, Ali has 4x more, how many more does Ali have? What is the total of the cards added together?
Answers
Answer:
Ali has 1528. She has 1146 more cards than Max. In total, there are 1910 cards.
Step-by-step explanation:
382 x 4 = 1528
1528 - 382 = 1146
1528 + 382 = 1910
Answer:
If Max=382 and Ali=4x\(4x = 4 \times 382 = 1448\)total cards added together is 328+1448=2776Convert 48 2/5 into a decimal
Answers
Answer:
48 and 2/5 converted into decimal form is 48.4
Answer:
\(48.4\)
Step-by-step explanation:
\(48 \frac{2}{5} \\ \frac{242}{5} \frac{ \times 20}{ \times 20} = \frac{4840}{100} \\ = 48.4\)
The set of order pairs representing a function is given
(1,3),(2,3),(5,6)
Select all of the pairs that could be included in the set so that it remains a function
Answers
(4,8) and (6,10) are the pairs that could be included in the set so that it remains a function.
Difference Quotient Problem

Answers
The difference quotient expression for the given function is
\(\frac{f(x+h)-f(x)}{h} =\frac{\sqrt{(x+h+1)(x+h-1)}-\sqrt{(x+1)(x-1)} }{h}\)
Difference Quotient Formula:The expression in single-variable calculus is usually referred to as the difference quotient.
\(\frac{f(x+h)-f(x)}{h}\)
When taken to the limit as h gets closer to zero, h frac f(x+h)-f(x)h, which gives the derivative of the function f.
The slope of a secant line passing through the curve of f(x) is measured by the difference quotient.
Consider the difference quotient formula,
\(\frac{f(x+h)-f(x)}{h}\)
Evaluate the function at x = x + h
replace the variable x with (x + h) in the given expression
\(f(x+h)=\sqrt{(x+h)^2-1}\)
simplify the result ,
\(f(x+h)=\sqrt{(x+h+1)(x+h-1)}\)
find the components of the definition,
\(f(x+h)=\sqrt{(x+h+1)(x+h-1)}\)
\(f(x)=\sqrt{(x+1)(x-1)}\)
plug in the components,
\(\frac{f(x+h)-f(x)}{h} =\frac{\sqrt{(x+h+1)(x+h-1)}-\sqrt{(x+1)(x-1)} }{h}\)
Learn more about difference quotient , visit:
https://brainly.com/question/29054033
#SPJ1
The distance between Dania and Hollywood is shown on the map. What is the actual distance between Dania and Hollywood?
please help it is due in 15 min

Answers
Answer:
15 miles
Step-by-step explanation:
If there are 2.5 inches and 1 inch is 6 miles, then just multiply 6 by 2.5 to get 15
6*2.5=15
giải phương trình Bermolli : y' +\(\frac{y}{x}\) =x\(y^{2}\)
Answers
Answer:
y(x) = -1/(x^2 + c_1 x)
Step-by-step explanation:
Solve Bernoulli's equation ( dy(x))/( dx) + y(x)/x = x y(x)^2:
Divide both sides by -y(x)^2:
-(( dy(x))/( dx))/y(x)^2 - 1/(x y(x)) = -x
Let v(x) = 1/y(x), which gives ( dv(x))/( dx) = -(( dy(x))/( dx))/y(x)^2:
( dv(x))/( dx) - v(x)/x = -x
Let μ(x) = e^( integral-1/x dx) = 1/x.
Multiply both sides by μ(x):
(( dv(x))/( dx))/x - v(x)/x^2 = -1
Substitute -1/x^2 = d/( dx)(1/x):
(( dv(x))/( dx))/x + d/( dx)(1/x) v(x) = -1
Apply the reverse product rule f ( dg)/( dx) + g ( df)/( dx) = d/( dx)(f g) to the left-hand side:
d/( dx)(v(x)/x) = -1
Integrate both sides with respect to x:
integral d/( dx)(v(x)/x) dx = integral-1 dx
Evaluate the integrals:
v(x)/x = -x + c_1, where c_1 is an arbitrary constant.
Divide both sides by μ(x) = 1/x:
v(x) = x (-x + c_1)
Solve for y(x):
y(x) = 1/v(x) = -1/(x^2 - c_1 x)
Simplify the arbitrary constants:
Answer: y(x) = -1/(x^2 + c_1 x)
The expression (g^2)^4 is equivalent to g^m. What is the value of m?
^ means exponents
Answers
Answer:
m = 8
Step-by-step explanation:
4 x 2
you just have to multiply exponents
Evaluate the function f(x) =x/2-5
For x=-3
F(-3)
Answers
Sal paid (x + 2y) cents for a quart of milk and (2x + y) cents each for three cartons of orange juice. Write and simplify an expression for the total cost of Sal's purchases.
Answers
The expression for the total cost of Sal's purchases is 7x + 5y cents.
We know that Sal paid (x + 2y) cents for a quart of milk and (2x + y) cents each for three cartons of orange juice.To find the total cost of Sal's purchases we need to add the cost of the milk and the cost of the three cartons of orange juice and simplify the expression.The cost of the milk is given as (x + 2y) cents. The cost of three cartons of orange juice is (2x + y) cents each.
Therefore, the cost of three cartons of orange juice is (3 × (2x + y)) cents. To find the total cost of Sal's purchases, we add the cost of the milk and the cost of the three cartons of orange juice.(x + 2y) + (3 × (2x + y)) cents = x + 2y + 6x + 3y cents= 7x + 5y cents.
For more questions on cost
https://brainly.com/question/2292799
#SPJ8
please soleeeeeeeeeeeeèeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee

Answers
Step-by-step explanation:
Answer is 99. I am pretty sure.
Which is an equation of the line that passes through (4, -5) and (6, 9)?
Answers
Answer:
try 21 x 21 plus 21 divided by 21 then add 21 x 21
Step-by-step explanation:
easy math
Answer:
\(y=7x-33\)
Step-by-step explanation:
\(m=\frac{9-(-5)}{6-4}\\m=\frac{14}{2}\\m=7\\y=7x+b\\b=-5-(7)(4)\\b=-33\\y=7x-33\)
-15.5. - 15. - 14.5, -14, ...
What is this in explicit formula
Answers
Answer:
the numbers are going down by .5 nvm I answered this wrong.
My salary is £28,860 per year. What is my hourly rate of pay if I work 37 hours a week
Answers
Answer:
pay rate £7.80
Step-by-step explanation:
28860 divide by 37 = 780
780 divided by 100 = 7.80
PLEASE HELP ASAP
prove the identity:
sec x sin x
—————— =sin^2x
tan x+cot x
Options in pic

Answers
Answer:
See below
Step-by-step explanation:
\(\displaystyle \frac{\sec x\sin x}{\tan x+\cot x}\\\\=\frac{\frac{1}{\cos x} \sin x}{\frac{\sin x}{\cos x} + \frac{\cos x}{\sin x}}\\ \\=\frac{\frac{\sin x}{\cos x} }{\frac{\sin x \sin x}{\cos x \sin x} + \frac{\cos x \cos x}{\cos x \sin x}}\\\\=\frac{\frac{\sin x}{\cos x} }{\frac{\sin^2 x}{\cos x \sin x} + \frac{\cos^2 x}{\cos x \sin x}}\\\\=\frac{\frac{\sin x}{\cos x}}{\frac{\sin^2 x+\cos^2 x}{\cos x \sin x} }\\ \\=\frac{\frac{\sin x}{\cos x} }{\frac{1}{\cos x \sin x} }\)
\(=\frac{\sin x}{\cos x}\cdot \sin x \cos x\\ \\=\frac{\sin x \sin x \cos x}{\cos x}\\ \\=\sin^2x\)
Thus, the identity is proven. Match the options up accordingly to my step-by-step process.
Given rhombus ABCD, find the area if mZABC = 60° and AE = 2.

Answers
The area of the rhombus, obtained from the dimensions, of the diagonals, found from the trigonometric of sines of the angle can be presented as follows;
Area = 8·√3
What is the area of a plane figure?The area of a plane figure is the two dimensional space occupied by the figure on a plane.
The measure of the angle ABC, m∠ABC = 60°
The length of the segment AE = 2 units
The diagonals of a rhombus bisect each other at right angles, and the right angles through which they pass, therefore;
BE = ED, m∠AEB = 90°
m∠ABE = 30°
sin(30°) = AE/AB
sin(30°) = 2/AB
AB = 2/(sin(30°)) = 4
AB = 4
BE = √(4² - 2²) = √(12) = 2·√3
Therefore; AC = 2 + 2 = 4
BD = 2·√3 + 2·√3 = 4·√3
The area of a rhombus = (1/2) × The product of the length of the diagonals
Therefore;
Area of the rhombus = (1/2) × (4·√3) × 4 = 8·√3
The area of the rhombus = 8·√3
Learn more on the area of a rhombus here: https://brainly.com/question/30985956
#SPJ1
Determine whether the graph defines a function of x.
Yes or No

Answers
Answer:
No.
Step-by-step explanation:
A function should never have a shape like this.
which of the following is equivalent to x^2 -5x +6
Answers
Hello!
x² - 5x + 6
= (x² - 2x) + (-3x + 6)
= x(x - 2) - 3(x - 2)
= (x - 2)(x - 3)
What is the length of the hypotenuse, x, if (20, 21, x) is a Pythagorean triple?
22
29
41
42
Answers
Answer:
B
Step-by-step explanation:
The length of the hypotenuse, x, if (20, 21, x) is a Pythagorean triple is 29.
What is Pythagorean triples?Pythagorean triples are represented as the triple (a, b, c) where a represents the perpendicular side, b represents the base and c represents the hypotenuse.
Pythagoras theorem states that for a right angled triangle, the square of the hypotenuse is the sum of the squares of base and altitude.
c² = a² + b²
Here a = 20, b = 21 and c = x.
x² = 20² + 21²
x² = 841
x = √841 = 29
Hence the length of the hypotenuse, x, is 29.
Learn more about Pythagorean Triples here :
https://brainly.com/question/15190643
#SPJ5
I’m trying to complete old work but this assignment was some time ago and I do not remember the steps to it

Answers
Given:
\(\sin\theta=\frac{5}{13}\)Required:
To find the value of
\(\cos2\theta\)Explanation:
We know that
\(\cos2\theta=1-2\sin^2\theta\)\(\begin{gathered} =1-2(\sin\theta)^2 \\ \\ =1-2(\frac{5}{13})^2 \\ \\ =1-2(\frac{25}{169}) \\ \\ =1-\frac{50}{169} \\ \\ =\frac{169-50}{169} \\ \\ =\frac{119}{169} \end{gathered}\)Final Answer:
\(\cos2\theta=\frac{119}{169}\)In a package of candy there is a total of 24 yellow pieces. For every 5 green pieces in the package, there are 8 yellow pieces. How many green pieces of candy are in the bag?
Answers
Answer:
15 green pieces.
Step-by-step explanation:
8x = 24
x = 3.
So you need 3 times the amount of green pieces for every yellow piece.
3 * 5 green pieces = 15 green pieces
giving brainliest ! *easy*

Answers
Answer:
170
Step-by-step explanation:
17π/18 * 180/π
17*180/18
=170
In How Many Different Ways Can A Player Select A Spadea) In how many different ways can a player select a spade and a heart from a deck of 52 bridge cards?ways(b) In how many different ways can a player select one card of each suit from a bridge deck?ways
Answers
Thus, there are 169 different ways that a player could choose a diamond and a club.
How Many Different Ways Can A Player Select A Spade?A deck of 52 bridge cards contains 13 cards in each of the four suits—diamond, spade, club, and hearts—for a total of 52 cards. One of the earliest activities can be thought of as diamond choosing. \($A_1$\) and the second endeavour \($A_2$\) determines which club to join. Apply the adage "If two things, multiply them by two." \($A_1$\) and \($A_2$\) is possible to perform in \($n_1$\) and \($n_2$\) many methods, correspondingly. The total number of ways that are then \($A_1$\) then comes \($A_2$\) being able to be done \($n_1 \times n_2$\) "
Here, \($n_1=13$\) and \($n_2=13$\), In the following rule, change the values as follows:
\($$\begin{aligned}n_1 \times n_2 & =13 \times 13 \\& =169\end{aligned}$$\)
The user can choose a diamond and a club in one of 169 different ways. When I see a SPADE, I should square the item to the left, square the item to the right, add the two items, and then take the square root of that sum.
To learn more about spade selection refer to :
https://brainly.com/question/1243126
#SPJ4
i need help i dont quite understand this and would be happy if someone helped

Answers
Answer: 2, 3, 6, 7
Step-by-step explanation:
Supplementary is two angles adding up to 180. The angles above with angle 5 add up to 180.
Gianna just started a running plan where she runs 20 miles the first week and then increases the number of miles she runs by 5% each week. If she keeps up this plan for 17 weeks, how many total miles would Gianna have run, to the nearest whole number?