In June 2003, an Italian named Giancarlo Bellingrath set a world record when
he held his breath for 12 minutes and 47 seconds. How many seconds is
this?
Answers
Answer:
767 Seconds
Step-by-step explanation:
60 seconds in a minute so 12 x 60 = 720
Then add the 47.
720 + 47 = 767
Answer:
59
Step-by-step explanation:
Related Questions
let p be a point chosen uniformly at random in the interior of the unit square with vertices at (0, 0),(1, 0),(1, 1), and (0, 1). the probability that the slope of the line determined by p and the point 5 8 , 3 8 is greater than or equal to 1 2 can be written as m n , where m and n are relatively prime positive integers. find m n
Answers
The probability that the slope of the line determined by p and the point (5/8, 3/8) is greater than or equal to 1/2 is 5/8.
Let the coordinates of point p be (x,y). Then, the slope of the line determined by p and the point (5/8, 3/8) is:
(slope) = (y - 3/8)/(x - 5/8)For the slope to be greater than or equal to 1/2, we must have:
(y - 3/8)/(x - 5/8) >= 1/2Solving for y, we get:
y >= (x/2) + 7/16Graphing this inequality on the unit square, we see that the region satisfying this inequality is a trapezoid with vertices (5/8,3/8), (1,1/2), (1,1), and (3/4,1).
The area of this trapezoid is (1/2)*((5/8 - 3/4) + (1 - 5/8) + (1 - 1/2) + (3/8 - 3/16)) = 5/16.
The area of the unit square is 1, so the probability we seek is 5/16.
Hence, the answer is 5/16 written as a fraction in its simplest form, which is 5/16.
Learn more about Probability:
https://brainly.com/question/24756209
#SPJ4
Find the total surface area of the figure below.

Answers
Answer:
240
Step-by-step explanation:
You have to find the area of each indivigual side and then add all the areas together. So like 9x5 is 45 so you take 45 and multiply it by 4 since there are 4 sides identical to that side and then you get 180. Then you multiply 6x5 and that gives you 30 which you then multiply by 60, so then all you gotta do is 60+180=240.
During science class, groups measure out different volumes of vinegar. The line plot below shows the amount of vinegar used by 12 1212 groups, rounded to the nearest 1 2 mL 2 1 mLstart fraction, 1, divided by, 2, end fraction, start text, space, m, L, end text. 4 4 4 1 2 4 2 1 5 5 5 1 2 5 2 1 6 6 6 1 2 6 2 1 7 7 7 1 2 7 2 1 8 8 A line plot labeled 4 to 8 with tick marks every one-half unit labeled with a tick mark and number. Above tick mark four and one-half there is a column of two dots. Above tick mark 5 there is a column of three dots. Above tick mark six and one-half there is a column of two dots. Above tick mark 7, there is a column of two dots. Above tick mark seven and one-half, there is a column of three dots. What is the total amount of vinegar, in milliliters, used by the 3 33 groups that used the most? mL mL
Answers
Answer:
22 1/2
Step-by-step explanation:
What is the meaning of "\(F=\left \{ (x,y):\varphi (x,y,p) \right \}\)"?
![What is the meaning of "[tex]F=\left \{ (x,y):\varphi (x,y,p) \right \}[/tex]"?](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/qPezzQZ7dJhdA0YcETQG5fBdyZW4BfQR.png)
Answers
The expression "F = {(x, y) : φ(x, y, p)}" represents a set of ordered pairs (x, y) that satisfy a condition defined by the function φ. The interpretation and nature of the set F depend on the specific function φ and the parameter p, which determine the relationship between the variables x, y, and p.
The expression "F = {(x, y) : φ(x, y, p)}" represents a set F consisting of ordered pairs (x, y) that satisfy a particular condition defined by the function φ, which takes the variables x, y, and p as inputs.
To fully understand the meaning of F, we need to delve into the function φ and its relationship with the variables x, y, and p. The function φ could represent a wide range of mathematical relationships or conditions that determine the inclusion of certain pairs (x, y) in the set F.
For instance, let's consider a specific example where vraphi(x, y, p) is defined φ(x, y, p) = \(x^2 + y^2 - p^2.\)In this case, F = {(x, y) : \(x^2 + y^2 - p^2\)= 0} represents a set of ordered pairs (x, y) that satisfy the equation \(x^2 + y^2 - p^2 = 0.\) This equation represents a circle with radius p centered at the origin (0, 0). Consequently, F corresponds to all the points lying on the circumference of this circle.
It is important to note that the specific meaning and implications of F heavily rely on the nature of the function φ and the parameter p. Different functions and parameters will yield distinct sets F with their own unique characteristics and interpretations.
For more such information on: expression
https://brainly.com/question/28602085
#SPJ8
Turn this into a formula and step by step on how to solve it.

Answers
What number completes the ordered pair (4, y) so that it is a solution of the function can be 2x+y=10
Answers
2(4)+y=10
8+y=10
10-8
y=2
If f (x) = 2 x + 5 and three-halves are inverse functions of each other and StartFraction 41
Answers
The inverse of the function → f(x) = 2x + 5 is → f⁻¹(x) = (x/2) - (5/2).
What is the procedure to find inverse of function ?Inverse of a function can be calculated by following the steps mentioned below -
Step 1 - Replace {y} with {x} and vice - versa.Step 2 - Rewrite the equation by solving for {y}.Step 3 - Replace {y} with f⁻¹(x).According to the question, the equation given is as follows
y = f(x) = 2x + 5
y = 2x + 5
Replace 'y' with 'x', we get -
x = 2y + 5
Now, solve for y -
2y = x - 5
y = (x/2) - (5/2)
Replace 'y' with f⁻¹(x) -
f⁻¹(x) = (x/2) - (5/2)
Hence, the inverse of the function → f(x) = 2x + 5 is → f⁻¹(x) = (x/2) - (5/2).
To solve more questions on inverse of function, visit the link below-
brainly.com/question/28229665
#SPJ1
Johnny and Elizabeth were playing a video game and trying to get all of the treasure Johnny got 1/3 and Elizabeth got 5/9 of the treasure . How much of the treasure did they get in all?
Answers
Answer:
8/9. 5/9+1/3 L.C.M =9 ANS= 8/9.
Help me!
A) SSS
B) ASA
C) SAS
D) SSA
Choose the right one!

Answers
How many solutions does the system of equations have? Explain1. Y = 5x - 4 Y = -4 + 5xNumber of solutions:Explain Why2. Y=2x+3 Y=-3x+63. Y=-4x+5 Y=-4x+5
Answers
The equations are
\(\begin{gathered} Y=5x-4 \\ Y=-4+5x \end{gathered}\)Solve the equations for varaible x.
\(\begin{gathered} 5x-4=-4+5x \\ -4=-4 \end{gathered}\)Since each side of the equation is equal to each other. So lines overlap each other and there are infinitely many solution for the equations.
PLEASE ANSWER ASAP I NEED IT.

Answers
Answer:
\(\huge\boxed{\sf 18^{-3}}\)
Step-by-step explanation:
Given expression:\(\displaystyle \frac{18^4}{18^7}\)
According to exponent rule:\(\displaystyle \frac{a^m}{a^n} = a^{m-n}\)So, the expression becomes:
= \(18 ^{4-7}\)
= \(18^{-3}\)
\(\rule[225]{225}{2}\)
The average natural gas bill for a random sample of 26 homes in the 19808 zip code during the month of March was $305.30 with a sample standard deviation of $46.50. The critical value for a 95% confidence interval around this sample mean is ________.
Answers
Answer:
2.06
Step-by-step explanation:
The formula for critical value = Margin of Error / Standard Error
Margin of Error = z × Standard deviation/√n
Mean for the month of March = $305.30
Standard deviation = $46.50
n = number of samples = 26 homes
z score for 95% confidence interval = 1.96
= 1.96 × $46.50/√26
= 17.874024556
Standard error = standard deviation/√n
= $46.50/√26
= 9.1194002839
Critical value = Margin of Error/Standard Error
= 17.874024556/9.1194002839
= 2.06
I’m am so lost please help thank you all

Answers
Answer:
Step-by-step explanation:
148 people
Given f(x)=x^2+6x and g(x)=4 x^2, find fg. fg(x)=
Answers
The composite function f·g(x) is 4x⁴+24x³.
The given functions are f(x)=x²+6x and g(x)=4x².
We need to find f·g(x).
We know that, f·g(x)=f(x)×g(x)
Here, f·g(x)=(x²+6x)×4x²
= x²×4x²+6x×4x²
= 4x⁴+24x³
Therefore, the composite function f·g(x) is 4x⁴+24x³.
To learn more about the function visit:
https://brainly.com/question/28303908.
#SPJ1
Carlos works at an electronics store selling computer equipment. He can earn a bonus if he sells
$10,000 worth of computer equipment this month. So far this month, he has sold $4000 worth of
computer equipment. He hopes to sell additional laptop computers for $800 each to reach his goal.
The function f(x) = 800x + 4000 represents Carlos's total sales as a function of the number of laptop
computers he sells.
Answers
Answer:
lol i hope this helps:
Step-by-step explanation:
:3 (look at the photo!!!)


Ralph wants to join a travel soccer team, a discretionary expense.
His parents tell him he must get a job to earn the money to cover the costs. Ralph now views this discretionary expense as an essential expense since he must pay his parents back. The costs of the travel team are listed below.
Uniform - $67.00
Registration - $50.00
Tournaments -$775.00
Travel - $300.00
a. Find the total cost of being on the team.
b. If Ralph takes a summer job and works 10 weeks over the summer, how much must he average each week to cover the travel team expenses?
c. If Ralph is paid at a flat rate of exactly q dollars each week, what is the standard deviation of the distribution of his 10 weekly paychecks?
Answers
a) The total cost of being on the team is; $1192
b) Ralph average cost is; $119.20
c) The standard deviation of the distribution of his 10 weekly paychecks is; $0
What is the Total Cost?
We are given the costs of the travel team as listed below;
Uniform - $67.00
Registration - $50.00
Tournaments -$775.00
Travel - $300.00
a) To find the total cost of being on the team, we will simply add all the individual costs as given to get;
Total Cost = 67 + 50 + 775 + 300
Total Cost = $1192
b) If Ralph takes a summer job and works 10 weeks over the summer, then his average cost is;
Average Cost = 1192/10
Average Cost = $119.20
c) If he is paid at a flat rate of exactly q dollars each week, the standard deviation of the distribution of his 10 weekly paychecks is;
$0
Read more about Total Cost at; https://brainly.com/question/25109150
#SPJ1
Answer:
Step-by-step explanation:
first one is wrong and I don’t know the answer yet
PLEASSSSSSSSSSSSEEE HELPPP
69=-3(-3-4p)
Answers
Answer:
p = 5
Step-by-step explanation:
-3(-3-4p) = 69
-3×(-3) + -3× (-4p) = 69
9 + 12p = 69
12p + 9 - 9 = 69 - 9
12p = 60
p = 5
Hope this helps!!!
cuanto es 99+85+23+1231141221+52154234+265326355
Answers
1548622017
The sum of two numbers is −14. One number is 23 more than the other one. Find the numbers.
Answers
Answer:
below
Step-by-step explanation:
x = one number
x+23 = second number <======added together the equal -14
x + x+23 = -14
2x = -37
x = -18.5 other number = x+23 = 4.5
Find the perimeter of this shape

Answers
The perimeter of the given shape as represented in the task content is; 29 cm.
What is the perimeter of the given shape?It follows from the task content that the perimeter of the given shape on the centimeter grid as required is to be determined.
Since each grid line has 1cm as it's length;
The perimeter of the shape is the sum of all side lengths of the shape;
Perimeter, P = 6+2+3+2+2+1+3+2+2+2+2+1
P = 29 cm
Hence, the perimeter of the shape is; 29 cm.
Read more on perimeter of a shape;
https://brainly.com/question/303508
#SPJ1
SOMEBODY HELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIEST
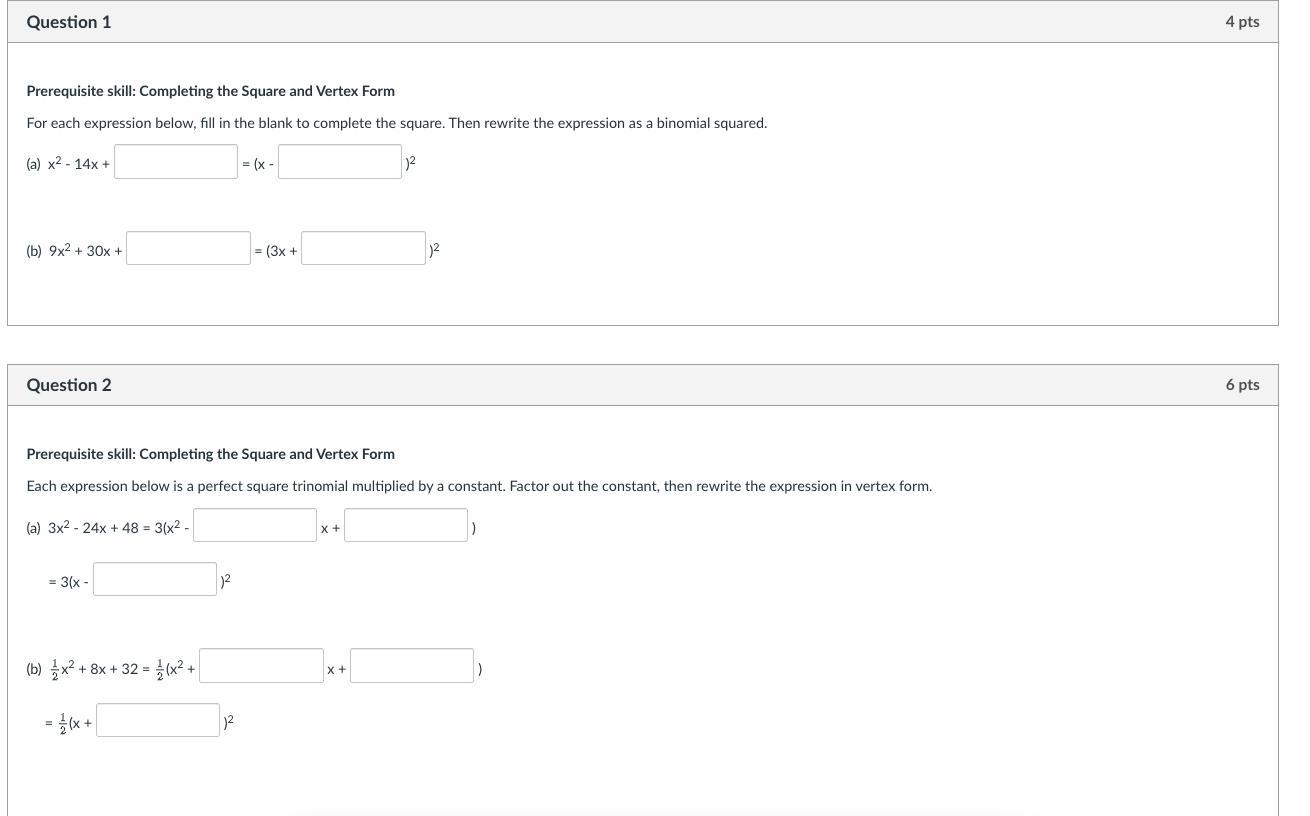
Answers
Answer:
\(\textsf{1.(a)} \quad x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
\(\textsf{1.(b)} \quad 9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\begin{aligned}\textsf{2.(a)}\quad3x^2-24x+48&=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\\&=3\left(x-\boxed{4}\right)^2\end{aligned}\)
\(\begin{aligned}\textsf{2.(b)}\quad \dfrac{1}{2}x^2+8x+32&=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\\&=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\end{aligned}\)
Step-by-step explanation:
Question 1(a) When completing the square for a quadratic equation in the form ax² + bx + c where the leading coefficient is one, we need to add the square of half the coefficient of the x-term:
\(x^2-14x+\left(\dfrac{-14}{2}\right)^2\)
\(x^2-14x+\left(-7\right)^2\)
\(x^2-14x+49\)
We have now created a perfect square trinomial in the form a² - 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Therefore:
\(a^2=x^2 \implies a=1\)
\(b^2=49=7^2\implies b = 7\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
(b) When completing the square for a quadratic equation where the leading coefficient is not one, we need to add the square of the coefficient of the x-term once it is halved and divided by the leading coefficient, and then multiply it by the leading coefficient:
\(9x^2 + 30x +9\left(\dfrac{30}{2 \cdot 9}\right)^2\)
\(9x^2 + 30x +9\left(\dfrac{5}{3}\right)^2\)
\(9x^2 + 30x +9 \cdot \dfrac{25}{9}\)
\(9x^2 + 30x +25\)
We have now created a perfect square trinomial in the form a² + 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 +2ab + b^2 = (a +b)^2}\)
Therefore:
\(a^2=9x^2 = (3x)^2 \implies a = 3x\)
\(b^2=25 = 5^2 \implies b = 5\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\hrulefill\)
Question 2(a) Factor out the leading coefficient 3 from the given expression:
\(3x^2-24x+48=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\)
We have now created a perfect square trinomial in the form a² - 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=3\left(x-\boxed{4}\right)^2\)
(a) Factor out the leading coefficient 1/2 from the given expression:
\(\dfrac{1}{2}x^2+8x+32=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\)
We have now created a perfect square trinomial in the form a² + 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2+2ab + b^2 = (a +b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\)
Step-by-step explanation:
Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
PLEASE HELP DUE IN 3 minutes

Answers
Answer:
Answer is B
Step-by-step explanation:
-40× +5y -125=0 relates y
Answers
Answer: −200y−125
Step-by-step explanation:
Solve the following for θ, in radians, where 0≤θ<2π.
4sin2(θ)+7sin(θ)−5=0
Select all that apply:
2.57
1.37
1.05
2.35
0.58
1.88
Answers
Answer:θ ≈ 2.57 radians
θ ≈ 0.58 radians
Step-by-step explanation:We can solve this quadratic equation in sin(θ) by factoring:
4sin^2(θ) + 7sin(θ) - 5 = 0
(4sin(θ) - 1)(sin(θ) + 5) = 0
Therefore, either:
4sin(θ) - 1 = 0
sin(θ) = 1/4
or:
sin(θ) + 5 = 0
sin(θ) = -5 (not possible, since sin(θ) is between -1 and 1)
So, we have sin(θ) = 1/4. Since 0 ≤ θ < 2π, we can find the two solutions in the interval [0, 2π) by using the inverse sine function:
θ = arcsin(1/4)
Using a calculator, we find:
θ ≈ 0.2531 or θ ≈ 2.8887
Therefore, in radians, the solutions for θ are approximately:
0.2531 (which is less than 2π)
2.8887 (which is greater than 2π)
So the only answer that satisfies 0 ≤ θ < 2π is:
URGENT!! ILL GIVE BRAINLIEST! AND 100 POINTS

Answers
The equation for the total cost of all adult tickets (a) and student tickets (s).
4a + 2.5s = 2,820
a + s = 900
The number of adults ticket and student tickets is 380 and 520.
We have,
Adults ticket cost = $4
Student ticket cost = $2.5
Now,
Total amount earned = $2,820
The equation for the total cost of all adult tickets (a) and student tickets (s).
4a + 2.5s = 2,820 ______(1)
And,
The number of tickets sold = 900.
We can write as equation as:
a + s = 900 ______(2)
Now,
We have two equations.
4a + 2.5s = 2820
a + s = 900
Solving for s.
s = 900 - a
Substituting in (1)
4a + 2.5(900 - a) = 2820
Simplifying and solving for a.
4a + 2250 - 2.5a = 2820
1.5a = 570
a = 380
Now,
a + s = 900
380 + s = 900
s = 520
Therefore,
The number of adults ticket and student tickets is 380 and 520.
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ1
The perimeter of Tamara's suitcase is 8x - 3 and the perimeter of Anna's suitcase is
3x + 2. Write an algebraic expression that represents
the difference between the perimeter of Tamara's suitcase
and the perimeter of Anna's suitcase?
Answers
Answer:
perimeter: 2
Step-by-step explanation:
8x-3 = 6x
8x – 6x = 3
2x = 3
x = 3/2
The required algebraic expression that represents the difference between the perimeter of Tamara's suitcase and the perimeter of Anna's suitcase is 5x - 5.
What are equation models?The equation model is defined as the model of the given situation in the form of an equation using variables and constants.
Here,
The difference between the perimeter of Tamara's suitcase and Anna's suitcase can be found by subtracting the expression for the perimeter of Anna's suitcase from the expression for the perimeter of Tamara's suitcase:
(8x - 3) - (3x + 2)
Simplifying the expression by removing the parentheses and combining like terms, we get:
8x - 3 - 3x - 2
= 5x - 5
Therefore, the algebraic expression that represents the difference between the perimeter of Tamara's suitcase and the perimeter of Anna's suitcase is 5x - 5.
Learn more about models here:
https://brainly.com/question/22591166
#SPJ7
Examine the triangle below. Use it to answer question 31.
Question 3
What type of trangle is shown?
Acute Equilateral Triangle
Acute Scalen Triangle
C. Obuse Scalene Triangle
D. Right Isosedes Triangle

Answers
Answer:
It’s blurry but I think it’s an obtuse triangle
Step-by-step explanation:
Maybe a right triangle
Let the positive numbers a, b, c. Prove that \(\frac{a^{2013}+b^{2013}+c^{2013} }{a^{2012}+b^{2012}+c^{2012}} \geq \frac{a+b+c}{3\\}\)
Answers
Answer:
I don't need to prove it, I already believe you
Anyone good with calculus? Please help.

Answers
First take a time derivative of a function describing motion,
\(\frac{d}{dt}h(t)=\frac{d}{dt}-4.9t^2+19.6t-14.6=-9.8t+19.6\).
Finding the maxima of the function is obtained by determining where the critical points are. You can find the critical points by equating the derivative with 0 and solving for t,
\(\frac{d}{dt}h(t)=0\)
\(-9.8t+19.6=0\implies t=\frac{19.6}{9.8}=\boxed{2}\).
So at 2 seconds the ball peaks in height.
To find out the height feed 2 to the function h.
\(h(2)=-4.9\cdot2^2+19.6\cdot2-14.6=\boxed{5}\).
So at 2 seconds the ball reaches maximum height of 5 meters.
Hope this helps :)
can someone help me answer this question please!!

Answers
Answer:
i think its A
Step-by-step explanation: