In Mrs. Clarito's farm, the ratio of goat to cow is 5:6. If there are 25 goats, how
many cows does she have?
A) 10
B) 20
C) 30
D) 40
Answers
Related Questions
Help:
The matrix equation represents a system of equations.
A matrix with 2 rows and 2 columns, where row 1 is 2 and 5 and row 2 is 1 and 3, is multiplied by matrix with 2 rows and 1 column, where row 1 is x and row 2 is y, equals a matrix with 2 rows and 1 column, where row 1 is 7 and row 2 is 5.
Solve for x and y using matrices. Show or explain all necessary steps.

Answers
Answer:
(x,y)=(-4,3)
Step-by-step explanation:
[2 5][x] = [7]
[1 3][y] [5]
[2 5 | 7] <-- Write the augmented matrix
[1 3 | 5]
[1 5/2 | 7/2] <-- (1/2)R1
[1 3 | 5 ]
[1 5/2 | 7/2] <-- R2-R1
[0 1/2 | 3/2]
[1 5/2 | 7/2] <-- 2R2
[0 1 | 3 ]
[1 0 | -4 ] <-- R1-(5/2)R2
[0 1 | 3 ]
RREF is achieved using Gaussian-Jordan Elimination. Therefore, the solution is (-4,3).
Biology application. The approximate number of calories C that an animal needs each day is given by
c = 72m 2/4, where m is the animal mass in kilograms.
Find the number of Calories that a 16 kg bear needs each day. To solve this, evaluate the equation when
m = 16.
Please help I will give Brainliest.
Answers
Answer:
C = 288 kg
Step-by-step explanation:
Given:
C = 72m^2/4
where,
C = approximate number of calories
m = animal mass in kilograms.
Find C when m = 16
C = 72m^2/4
= 72 * (16)^2/4
= 72 * (16)^1/2
= 72 * √16
= 72 * 4
= 288
C = 288 kg
A senior class saves money for the school prom. The class currently has $400 saved and wants a total of $7,600 for the prom. The class saves $80 each day.
Part B: How much does the class save, in total, after 25 days?
A) $4500
B) $3500
C) $2400
D) $1400
Answers
Answer: B
Step-by-step explanation:
Answer:
C
Step-by-step explanation:
80*25=2000
2000+400=$2400
Calculate the value of ra so that the following configuration is valid. R1 = 16 r2 = 2. 8 r3 = 2 vs = 72 vout = 64 (round off to two decimal places)
Answers
The value of Ra that makes the configuration valid is approximately 38.4.
To calculate the value of ra in order to have a valid configuration, we can use the voltage divider formula. The voltage divider formula is given by:
Vout = (Ra / (Ra + Rb)) * Vin
In this case, Ra is the unknown value we need to find, Rb is the sum of r2 and r3, and Vin is vs. We are given the following values:
R1 = 16
r2 = 2.8
r3 = 2
vs = 72
Vout = 64
First, let's find Rb:
Rb = r2 + r3 = 2.8 + 2 = 4.8
Now, we can rearrange the voltage divider formula to solve for Ra:
Ra = (Vout / Vin) * (Ra + Rb)
Substituting the given values:
Ra = (64 / 72) * (Ra + 4.8)
Simplifying the equation:
Ra = (8 / 9) * (Ra + 4.8)
Multiplying both sides by 9 to eliminate the fraction:
9 * Ra = 8 * (Ra + 4.8)
9Ra = 8Ra + 38.4
Subtracting 8Ra from both sides:
Ra = 38.4
Therefore, the value of Ra that makes the configuration valid is approximately 38.4.
To know more about voltage visit:
https://brainly.com/question/30765443
#SPJ11
the base and the height of a parallelogram are 18cm, and 23cm. if its base is decreases by 50%, calculate its new area.
Answers
The new area of the parallelogram is 207 cm², the area of a parallelogram is calculated by multiplying the base by the height. In this problem, the base is 18 cm and the height is 23 cm.
So, the original area of the parallelogram is 18 * 23 = 414 cm².If the base is decreased by 50%, the new base will be 18 / 2 = 9 cm. The new area of the parallelogram is then 9 * 23 = 207 cm².
Here are some additional explanations:
The base of a parallelogram is the side that is parallel to the other side.The height of a parallelogram is the perpendicular distance between the two bases.The area of a parallelogram is calculated by multiplying the base by the height.If the base of a parallelogram is decreased, the area of the parallelogram will also decrease.To know more about area click here
brainly.com/question/13194650
#SPJ11
For what values of x is the absolute value function ƒ(x) = −|x + 3| − 4 decreasing?
Answers
By identifying the vertex of the function, we conclude that it is decreasing for:
\(x < -3\)
For what values of x is the function increasing?Here we have an absolute value function:
\(f(x) = -|x + 3| - 4\)
This absolute value function has a positive coefficient, which means that the function opens downwards, so it looks like a regular "down" letter.
The function is decreasing when, reading from right to left, we see that the line goes downwards. And for functions like this, this happens for values of x smaller than the vertex x-value.
For:
\(f(x) = -|x + 3| - 4\)
The vertex is at (-3, -4)
Then the function is decreasing for \(x < -3\)
Learn more about absolute value functions:
brainly.com/question/5012769
pls help me classify this asap?!?!


Answers
Since all the angles of the first triangle are different, it is a scalene triangle, Similarly, since all the sides of the second triangle is also different, it is a scalene triangle.
Classification of trianglesTriangles is a 3-D shape with 3 sides and angles. The types of triangle that we have include;
ScaleneIsoscelesEquilateralObtuseRight triangleSince all the angles of the first triangle are different, it is a scalene triangle, Similarly, since all the sides of the second triangle is also different, it is a scalene triangle.
Learn more on triangle classification here: https://brainly.com/question/21535569
#SPJ1
#
f(x) = x
f(x) = 3
5
6
f(x)=3-x
f(x) = 1
Domain
3
0
x=2
2
f(x) = 2
Function Equation
f(x) = 5-x
Answers
f(x) = x is a simple linear function with a slope of 1, f(x) = 3 5 6 is a constant function, f(x) = 3-x is a linear function with a negative slope of -1, f(x) = 1 is a constant function, f(x) = 2 is a constant function
What is a constant function?A constant function is a mathematical function whose output value is the same for every input value
From the given parameters, f(x) = x is a simple linear function with a slope of 1, this implies that for every unit increase in x, the value of y increases by 1.
Also, f(x) = 3 5 6 is a constant function, where the value of y is always 3 5 6, regardless of the value of x.
In the same way, f(x) = 3-x is a linear function with a negative slope of -1, which means that for every unit increase in x, the value of y decreases by 1. The fourth function f(x) = 1 is a constant function, where the value of y is always 1, regardless of the value of x.
The domain of the fifth function is 3 0, which means that x can take any value between 3 and 0.
The sixth function f(x) = 2 is a constant function, where the value of y is always 2, regardless of the value of x.
Learn more about domain of a function on https://brainly.com/question/28599653
#SPJ1
find the value of the variables, giving brief reasons for your answer:
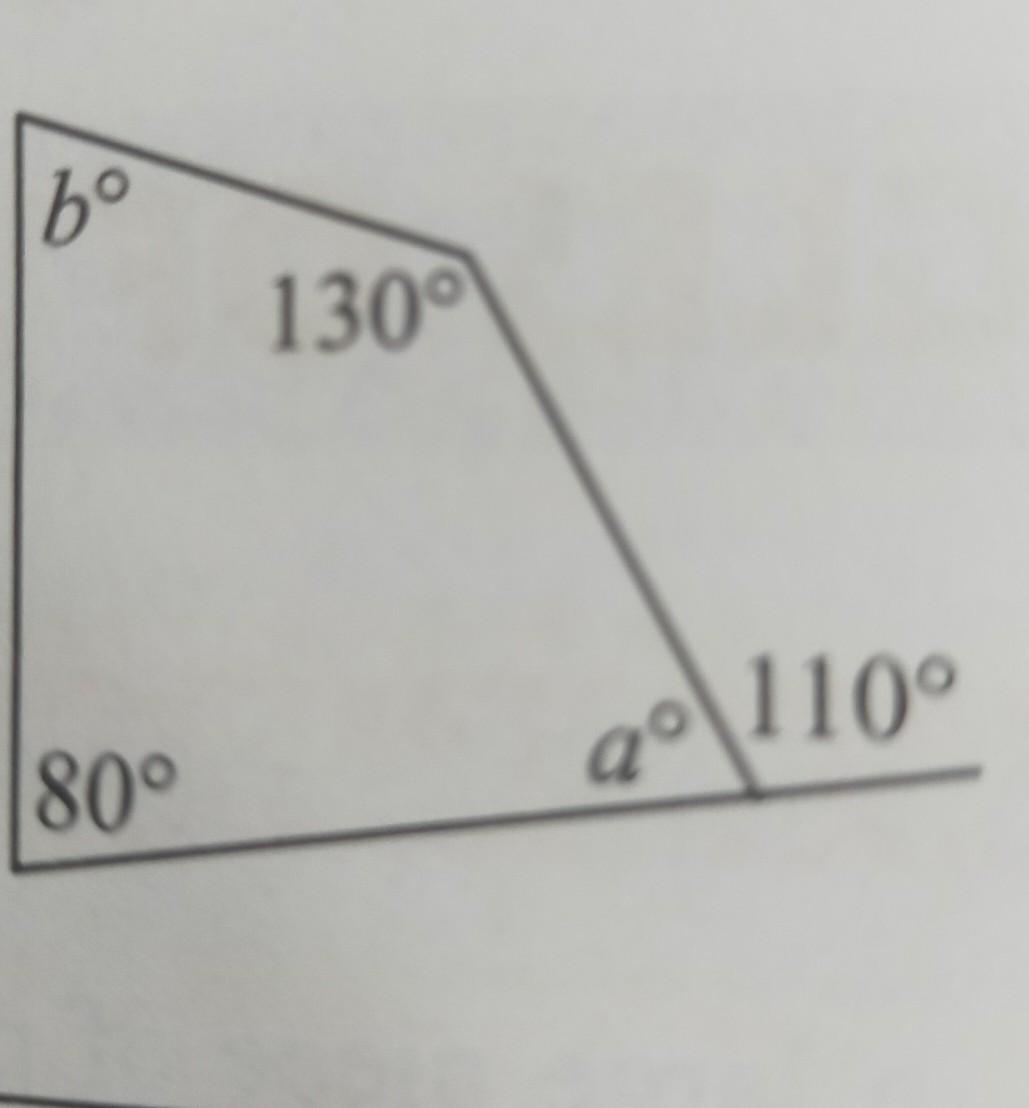
Answers
Answer:
a = 70°
b = 80°
Step-by-step explanation:
Angles on a straight line add up to 180°
⇒ a + 110 = 180
⇒ a = 180 - 110
⇒ a = 70°
The sum of the interior angles of a quadrilateral is 360°
⇒ a + b + 130 + 80 = 360
⇒ 70 + b + 130 + 80 = 360
⇒ b + 280 = 360
⇒ b = 360 - 280
⇒ b = 80°
please help I will give you any award

Answers
Answer:
218.57
Step-by-step explanation:
Since it is an isoceles triangle, the sides are 32, 32, and 14.
Using Heron's Formula, which is Area = sqrt(s(s-a)(s-b)(s-c)) when s = a+b+c/2, we can calculate the area.
(A+B+C)/2 = (32+32+14)/2=39.
A = sqrt(39(39-32)(39-32)(39-14) = sqrt(39(7)(7)(25)) =sqrt(47775)= 218.57.
Hope this helps have a great day :)
Check the picture below.
so let's find the height "h" of the triangle with base of 14.
\(\begin{array}{llll} \textit{using the pythagorean theorem} \\\\ a^2+o^2=c^2\implies o=\sqrt{c^2 - a^2} \end{array} \qquad \begin{cases} c=\stackrel{hypotenuse}{32}\\ a=\stackrel{adjacent}{7}\\ o=\stackrel{opposite}{h} \end{cases} \\\\\\ h=\sqrt{ 32^2 - 7^2}\implies h=\sqrt{ 1024 - 49 } \implies h=\sqrt{ 975 }\implies h=5\sqrt{39} \\\\[-0.35em] ~\dotfill\)
\(\stackrel{\textit{area of the triangle}}{\cfrac{1}{2}(\underset{b}{14})(\underset{h}{5\sqrt{39}})}\implies 35\sqrt{39} ~~ \approx ~~ \text{\LARGE 218.57}\)

Central Middle School has calculated a 95% confidence interval for the mean height (μ) of 11-year-old boys at their school and found it to be 56 ± 2 inches.
(a) Determine whether each of the following statements is true or false.
There is a 95% probability that μ is between 54 and 58.
There is a 95% probability that the true mean is 56, and there is a 95% chance that the true margin of error is 2.
If we took many additional random samples of the same size and from each computed a 95% confidence interval for μ, approximately 95% of these intervals would contain μ.
If we took many additional random samples of the same size and from each computed a 95% confidence interval for μ, approximately 95% of the time μ would fall between 54 and 58.
(b) Which of the following could be the 90% confidence interval based on the same data?
56±1
56±2
56±3
Without knowing the sample size, any of the above answers could be the 90% confidence interval.
Answers
a)1. True
2.False
3.True
4).False
b)Without knowing the sample size and standard deviation, we cannot determine the exact 90% confidence interval.
(a) For the content loaded Central Middle School data:
1. True: There is a 95% probability that μ (mean height) is between 54 and 58 inches.
This is the correct interpretation of the 95% confidence interval.
2. False: The confidence interval doesn't tell us the probability of the true mean or the margin of error being exactly as given. It only tells us the range where the true mean is likely to fall with 95% confidence.
3. True: If we took many additional random samples of the same size and from each computed a 95% confidence interval for μ, approximately 95% of these intervals would contain μ. This is the definition of a 95% confidence interval.
4. False: It's incorrect to say that μ would fall between 54 and 58 95% of the time. The correct interpretation is that if we computed multiple 95% confidence intervals, approximately 95% of those intervals would contain the true mean height.
(b) To determine the 90% confidence interval based on the same data:
Without knowing the sample size and standard deviation, any of the above answers could be the 90% confidence interval. Confidence intervals depend on the sample size, standard deviation, and desired confidence level. With the information given, we cannot determine the exact 90% confidence interval.
To know more about Mean:
https://brainly.com/question/31101410
#SPJ11
Consider the discrete probability distribution below. Complete parts and to the right Outcome Probability 0.26 035 2 0.00 0.00 0 1 a. Calcutate the mean of this distibution - Type an integer or a decimal) b. Calculate the standard deviation of this distribution 0.18 3 4 5 6 0.04 0.02 (Round to three decimal places as needed.)
Answers
Given data: Outcome 0 1 2 Probability 0.26 0.35 0.39a)
The mean of the distribution is given by: Mean = $\sum x P(x)$The distribution can be represented as follows:
Outcome(x) Probability(P(x)) x P(x) 0 0.26 0 1 0.35 0.35 2 0.39 0.78 $\sum x P(x)=0+0.35+0.78=1.13$
Therefore, Mean = $\frac {\sum xP(x)}{n}=\frac {1.13}{3} =0.3767 ≈ 0.377$ (rounded to three decimal places)
b) The formula for standard deviation is given as: $$\sigma =\sqrt{\sum(x-\mu) ^2P(x)} $$where $\mu$ is the mean of the distribution
Substituting the given values in the above formula, we get:
\begin{align*}\sigma &=\sqrt{\sum(x-\mu) ^2P(x)} \\\sigma &=\sqrt{\sum(x-0.377) ^2P(x)} \end{align*} Outcome(x) Probability(P(x)) $x-μ$ $P(x)(x-μ)^2$ 0 0.26 -0.37746 0.03665 1 0.35 -0.02746 0.00076 2 0.39 1.01254 0.15709 Total 1 0.19450$$\sigma =\sqrt {0.1945}=0.441 ≈ 0.441$$
Therefore, the standard deviation of the distribution is approximately equal to 0.441 (rounded to three decimal places).
To know more about Probability refer to:
https://brainly.com/question/27342429
#SPJ11
A photograph measures five inches wide and six inches long. The picture is enlarged to fit on a wall. If the new larger picture is 150 inches wide, how long is it?
A)200 inches
B)250 inches
C)210 inches
D)180 inches
Answers
D, divide and figure out how much the picture is increasing lengthwise and use that to find the wideness
The dimension of the enlarge picture will be 150 inches (3.81 meters) wide and 180 inches (4.57 meters) long. Then the correct option is D.
What is dilation?Dilation is the process of increasing the size of an item without affecting its form. Depending on the scale factor, the object's size can be raised or lowered.
There is no effect of dilation on the angle.
A photograph measures 5 inches (0.13 meters) wide and 6 inches (0.15 meters) long.
The picture is enlarged to fit on a wall.
If the new larger picture is 150 inches (3.81 meters) wide.
Then the scale factor of the enlargement will be
Scale factor = 150 / 5
Scale factor = 30
Then the length of the picture will be
The length of the picture is given by the product of the scale factor and original length.
Length = 30 x 6
Length = 180 inches (4.57 meters)
Then the dimension of the enlarge picture will be 150 inches (3.81 meters) wide and 180 inches (4.57 meters) long.
Then the correct option is D.
More about the dilation link is given below.
https://brainly.com/question/2856466
#SPJ5
Will give brainliest
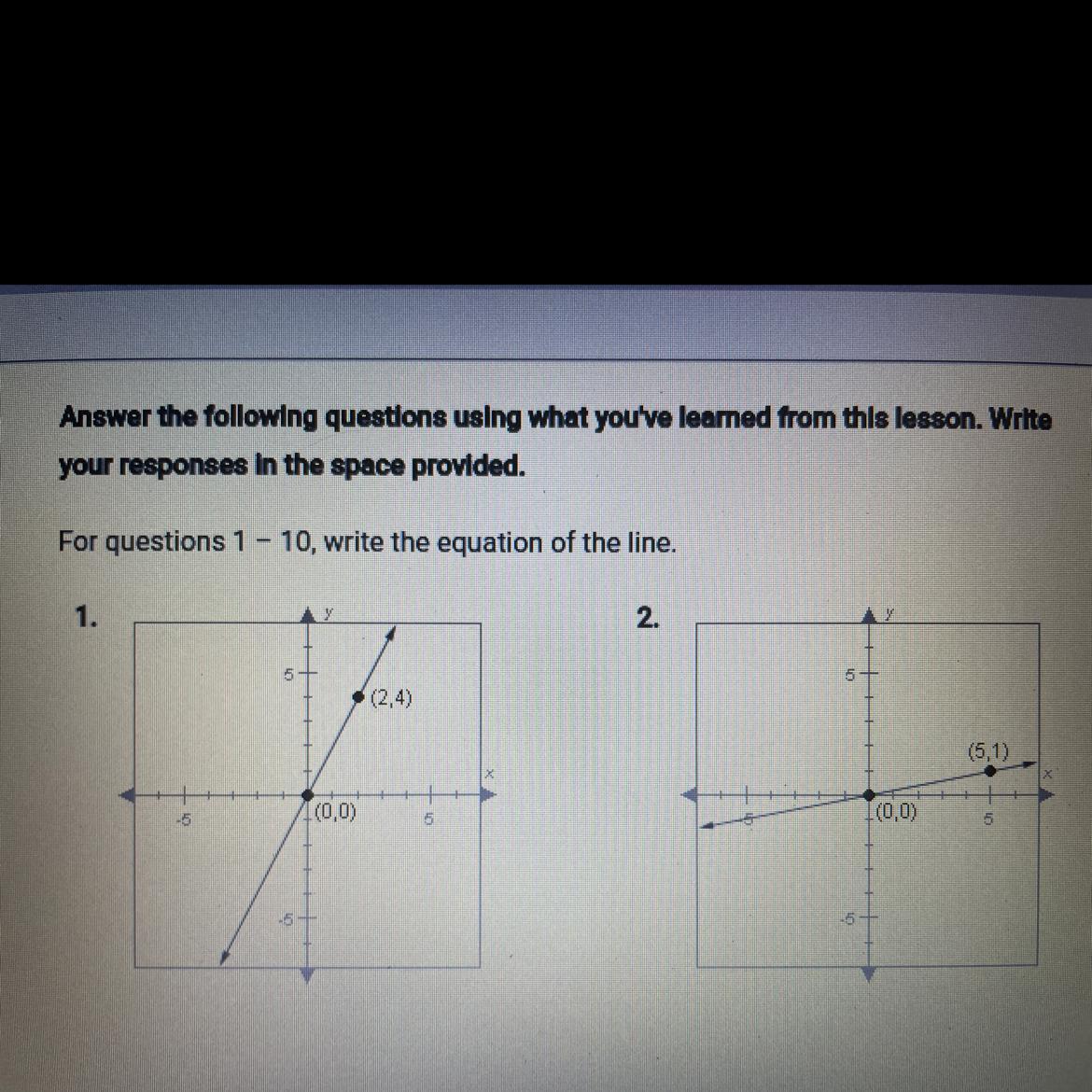
Answers
i cant see the question good enough
Answer:
1. y = 2x
2. y = 1/5x
Step-by-step explanation:
To write the equation of the line we need to find the slope and the y-intercept.
1. slope = y/x
4/2 = 2
y = 2x or y = 2x + 0
2.
1/5
y = 1/5x
How many wreaths could Diego make with the available ribbon
Answers
Answer:
9
Step-by-step explanation:
I feel like this is easy but I’m struggling

Answers
Answer:
There are several ways to put the coins one is 16 quarters and 5 dimes but 18 quarters could work as well
Step-by-step explanation:
400/25=16
50/10=5
450/25=18
a square whose side measures 2 centimeters is dilated by a scale factor of 3 . what is the difference between the area of the dilated square and the original square?
Answers
After figuring out the given issue, we discovered that the original square's area and the dilated square's area differ by 32 square centimeters.
What is the area of square formula?Square Area = Side x Side. Hence, Side2 square units are equivalent to the area of the square. and four side units make up a square's perimeter.
The formula for calculating the area of a initial square with sides that are 2 centimeters long is:
A = s²
A = 2²
A = 4 square centimeters
The revised side length of this square after dilation by a scale factor of 3 is:
s' = 3s
s' = 3(2)
s' = 6 centimeters
Calculations for the dilated square's area are as follows:
A' = s'²
A' = 6²
A' = 36 square centimeters
The area of a dilated square differs from the size of the original square by:
A' - A = 36 - 4
A' - A = 32 square centimeters
As a result, the original square's area and the dilated square's area differ by 32 square centimeters.
To know more about area of a square, visit:
https://brainly.com/question/30556035
#SPJ1
Find the amount of money Amber can afford to borrow using the banker's rule. Amber makes $32,300 annually. What is the amount that can be borrowed?
Answers
According to the banker's rule, Amber can afford to borrow a maximum of $96,900.
What is the amount that can be borrowed?
The banker's rule is a guideline used by some lenders to determine the maximum amount that an individual can borrow based on their annual income.
According to the banker's rule, the maximum amount that can be borrowed is typically a multiple of the borrower's annual income.
The exact multiple used in the banker's rule may vary depending on the lender and the borrower's financial situation, but a common multiple used is 3.
Therefore, to calculate the amount that Amber can afford to borrow using the banker's rule, we can multiply her annual income by 3.
Given that Amber makes $32,300 annually, we can calculate the amount that can be borrowed using the banker's rule as follows:
Maximum amount that can be borrowed = Annual income * Banker's rule multiple
Maximum amount that can be borrowed = $32,300 * 3
Maximum amount that can be borrowed = $96,900
Learn more about amount borrowed here: https://brainly.com/question/28959940
#SPJ1
express each of the following rational numbers as decimals
a,4/9
Answers
Step-by-step explanation:
-4/9 = -0.4444
Rounding the above number to 2 decimal places.
-0.44
a photograph is 5 inches by 8 inches. a frame shop charges $3.00 per inch for a silver frame. how much would it cost to buy a silver frame for the photograph?
Answers
Answer: The total cost for the frame is $78.00
Step-by-step explanation:
Photograph size = 5 inches x 8 inches
Perimeter = 5 + 5 +8 + 8
Perimeter =26 inches
Cost = $3.00 / inch for a silver frame
Total frame cost = 26 inches x $3.00 = $78.00
Please remember to vote this answer as Brainliest if I earned it!
Leon correctly found the slope and y-intercept of the line that passes through the points (9, –8) and (3, 4) as follows. m = StartFraction negative 8 minus 4 Over 9 minus 3 EndFraction = StartFraction negative 12 Over 6 EndFraction = negative 2. y = negative 2 x + b. Negative 8 = negative 2 (9) + b. Negative 8 = negative 18 + b. 10 = b. What is the equation of the line in slope-intercept form? y = negative 2 x + 10 y = 2 x + 10 y = 10 x minus 2 y = 10 x + 2
Answers
Answer:it’s a : y= -2x +10
Step-by-step explanation:
I just took the test and sorry I’m late
Step-by-step explanation:
y= -2x +10
How many different passcodes can be formed from the letters {a, b, c, d} if each letter can only be used once?.
Answers
The number of passcodes that can be formed from the letters {a, b, c, d} if each letter can only be used once is 24 according to permutations.
ni this problem we are not allowed to repeat the letters, so: we will be referring to the permutations, where Permutations are basically for the problems where the order or we can the arrangement matters
the formula for permutation is ⁿPr=n!/(n-r)! where n is the number of given letters and r is the number of letters to be used.here n and r are 4, substituting the values on the above formula, we get
⁴P₄=4!/(4-4)! = 4! = 4*3*2*1= 24
to know more about permutations refer to the link https://brainly.com/question/1216161?referrer=searchResults.
#SPJ4
PLEASE HELP HURRYYYYY

Answers
Answer:
See below
Step-by-step explanation:
Looks like positive linear to me....slope is up and to the right (positive) and the line drawn shows it ot be approx linear

Rodrigo compro 1/5 de los pasteles que venden la señora carmen , carlos 1/10 y francisca 1/3 del total . El resto de los pasteles no se vencio . Que parte del total aun esta disponible?
Answers
Se asume que en la pregunta: "El resto de los pasteles no se venció", se quiso decir en realidad: "El resto de los pasteles no se vendió".
Answer:
La parte del total que aún está disponible es \( \\ \frac{11}{30}\).
Step-by-step explanation:
El total de los pasteles que se compraron es la suma de las fracciones del total que compró Rodrigo, \( \\ \frac{1}{5}\), de la fracción del total que compró Carlos, \( \\ \frac{1}{10}\), y de la fracción del total que compró Francisca, \( \\ \frac{1}{3}\).
Numericamente hablando, Rodrigo, Carlos y Francisca compraron:
\( \\ \frac{1}{5}+\frac{1}{10}+\frac{1}{3}\) [1]
Del total de los pasteles que vende la Señora Carmen.
La suma de las fracciones en [1] se puede realizar de distintas maneras, una posible es la siguiente:
Podemos aplicar la propiedad asociativa para la suma, es decir, primero sumamos dos fracciones y el resultado lo sumamos a la fracción restante.Debemos recordar que, en general, en la suma de fracciones tenemos los siguientes casos:
Fracciones con denominadores diferentes
Si los denominadores de las fracciones son diferentes, los denominadores se multiplican. Este será el nuevo denominador para la suma de dos fracciones.Luego, cada denominador se multiplica con el numerador de la otra fracción. El resultado de cada multiplicación se suma y el total forma el nuevo numerador.Simplificar la fracción de ser posible, es decir, si el numerador y el denominador pueden dividirse por un mismo número, la división resultante para el numerador y el denominador formarán la nueva fracción. El número que simplifica la fracción a su "mínima expresión" es el máximo común divisor de ambos números.Fracciones con iguales denominadores
Se deja el mismo denominador y se suman los numeradores.Seguir el paso 3 del caso anterior para simplificar la fracción.De esta forma:
\( \\ (\frac{1}{5}+\frac{1}{10})+\frac{1}{3}\)
Se desarrolla primero la operación entre las fracciones dentro del paréntesis conforme a lo explicado anteriormente:
\( \\ (\frac{1*10+5*1}{5*10})+\frac{1}{3}\)
\( \\ (\frac{10+5}{50})+\frac{1}{3}\)
\( \\ \frac{15}{50} + \frac{1}{3}\)
Se divide el numerador y el denominador de la fracción \( \\ \frac{15}{50}\) entre cinco (5):
\( \\ (\frac{\frac{15}{5}}{\frac{50}{5}})+\frac{1}{3}\)
Resultando:
\( \\ (\frac{3}{10})+\frac{1}{3}\)
Esta fracción se suma a la siguiente y se procede de igual manera:
\( \\ \frac{3}{10}+\frac{1}{3}\)
\( \\ \frac{3*3+10*1}{10*3}\)
\( \\ \frac{9+10}{30}\)
\( \\ \frac{19}{30}\)
El número 19 es primo, es decir, sólo lo puede dividir el 1 y el mismo número (19). El 30 no es divisible por 19, por lo tanto, la fracción queda expresada de esa manera.Tenemos entonces que:
El total de los pasteles vendidos fue la fracción \( \\ \frac{19}{30}\).La parte que aún está disponible hay que restarla del total. El total es 1.De esta manera, la parte que aún está disponible es:
\( \\ 1 - \frac{19}{30}\)
Podemos hacer \( \\ 1 = \frac{30}{30} = 1\) (o un número dividido por si mismo es igual a la unidad) para que la operación se haga más fácilmente (caso de suma de fracciones con iguales denominadores):
\( \\ \frac{30}{30} - \frac{19}{30}\)
\( \\ \frac{30 - 19}{30}\)
\( \\ \frac{11}{30}\)
El número once es también un número primo y la fracción no se puede simplificar más porque el 30 no es divisible por 11.
Por lo tanto, la parte que aún está disponible es la fracción \( \\ \frac{11}{30}\), la cual podría interpretarse como once (11) partes de las treinta (30), \( \\ \frac{11}{30}\), que estaban disponibles antes de que Rodrigo, Carlos y Francisca compraran los pasteles.
(6d+5)−(2−3d) = what is the answer
Answers
\({ \red{ \bold{9d}}} \: + \: { \red{ \bold{3}}} \)
Step-by-step explanation:
\({ \blue{ \tt{(6d + 5)}}} - { \blue{ \tt{(2 - 3d)}}}\)
\({ \blue{ \tt{6d + 5 - 2 + 3d}}}\)
\( = { \blue{ \tt{9d + 3}}}\)
1/4x+2=2/3x+1/2 please help me
Answers
this is my answer, if you dont understand, dont be afraid to ask, hope this helps!

Help me down below
PLEASE

Answers
Answer:
the answer of the value of ten is 10000
Step-by-step explanation:
Answer:
Well the answer to the line is 55,000
Step-by-step explanation:
Not sure how to explain this. But if you count over to ones tens hundreds thousands and then ten thousands you should be at 55,000.
A spring has a rest length of 13 inches and a force of 12 pounds stretches the spring to a length of 18 inches. How much work is done stretching the spring from a length of 16 inches to a length of 25 inches?
Answers
The work done by stretching the spring from 16 inches to 25 inches is approximately 30.46 pound-inches.
We can start by calculating the spring constant k using Hooke's law.
F = kL0
k = F/L0 =12/13
Hooke's law states that the force required to compress or stretch a spring is directly proportional to the distance compressed or stretched, provided the elastic limit is not exceeded.The spring constant k can also be used to calculate the force required to compress or stretch the spring.
F = k (L-L0)
Where L is the length of the spring after being stretched or compressed.
Using the above equation, we can calculate the force required to stretch the spring from 16 inches to 25 inches.
F1 = k (16-13) = 12/13 * 3 = 36/13 pounds
F2 = k (25-13) = 12/13 * 12 = 144/13 pounds
Now, we can use the work-energy principle which states that the work done by a force is equal to the change in kinetic energy of the object the force is acting on, provided there is no change in potential energy.
W = ΔK = (1/2) m (v2 - v1)
where ΔK is the change in kinetic energy of the object, m is its mass, v2 is its final velocity, and v1 is its initial velocity. In this case, the object is the spring and its mass is negligible.
Therefore, the work done by stretching the spring from 16 inches to 25 inches is
W = (1/2) k [(25-13)2 - (16-13)2]
W = (1/2) (12/13) [(12)2 - (3)2] = 396/13 ≈ 30.46 pound-inches
The work done by stretching the spring is approximately 30.46 pound-inches.
Learn more about Work done:
https://brainly.com/question/25573309
#SPJ11
Use the normal approximation to find the indicated probability.
The sample size is n, the population proportion of successes is p,
and X is the number of successes in the sample.
n = 84, p = 0.4: P(X> 26)
Answers
The indicated probability is 0.07548.
When can we use the normal approximation to the binomial distribution?The binomial distribution is the probability of x successes on n trials, with p probability of a success on each trial. It can be approximated to the normal distribution with , as long as .
\(E(X) = np\\\\Var(X) = np(1-p)\)
we have that:
n = 84, p = 0.4: P(X> 26)
np = 84 x 0.4 = 33.6
n(1 - p) = 84 x 0.6 = 50.4 .
we can use the online binomial probability distribution calculator :
P(X≥ 26 ) = 0.07548
Hence the indicated probability is 0.07548.
More can be learned about the normal approximation to the binomial distribution at;
brainly.com/question/14424710
#SPJ1
I need help bro u will Mark u as the brainiest answer if u answer and it’s right!

Answers
Answer:
57.57% (round probably) for allergies and 42.42% for non allergies
Step-by-step explanation:
To find the percentage,
take the amount of people who have allergies and put it over the total number of people who speak two languages (33) and divide
19/33 x 100 = 57.57% (repeating so id round up to tenths)
same with no allergies
14/33 x 100 = 42.42% (also repeating)