In which of these pairs of numbers is 2 greater than the first and less than the second? 2.1, 2.3 2, 2 2.7, 3 2 , 2
Answers
Answer: most likely 2,2 I believe
Step-by-step explanation:
Related Questions
Domenic and Adriana are observing a hot-air balloon from two tracking stations on the ground.
The tracking stations are 6.0 km apart. From Domenic's point of view, the hot-air balloon is at an
angle of elevation of 72º. From Adriana's point of view, the angle of elevation is 58º.
Answers
Answer:
height of the balloon = 6.32 km
Step-by-step explanation:
The question wants us to find the height of the balloon .
They are observing the balloon from two tracking stations on the ground. The tracking stations are 6 km apart . From Dominic point of view the hair balloon is at an angle of elevation of 72° and from Adriana point of view the elevation is 58° . The illustration forms a triangle containing 2 right angles with a similar height.
To find the height we must find the hypotenuse of one of the right angle triangle. WE are given 2 angle and a side of 6 km. The third angle is 180 - 72 - 58 = 50°.
Using sin rule
6/sin 50° = b/sin 72°
cross multiply
6 sin 72° = b sin 50°
divide both sides by sin 50°
b = 6 sin 72°/sin 50°
b = 6 × 0.95105651629 /0.76604444311
b = 5.70633909777 /0.76604444311
b = 7.44909665372
b ≈ 7.45 km
The height can be found since we know the hypotenuse of one side of one of the right angle triangle.
sin 58° = opposite/hypotenuse
sin 58° = h/7.45
cross multiply
h = 7.45 × sin 58°
h = 7.45 × 0.84804809615
h = 6.31795831637
h ≈ 6.32 km
Help is needed please????

Answers
Answer: let F(x)=y
y=2x+5
Step-by-step explanation:
what the word form of 500.2
Answers
Answer:
How to Write Out USD 500.2 Dollars in Words: five hundred dollars and twenty cents.
I count on the best
how do you Simplify 6(x + 3).
Answers
Answer:
6x+18
Step-by-step explanation:
6(x + 3).
Distribute
6x+6*3
6x+18
what is the slope (5,7) and (2,-2)
Answers
Answer:
slope = 3
Step-by-step explanation:
to find the slope you do (y2-y1)/(x2-x1)=m
so we can plug the points into this formula
(5,7) (2,-2)
x1 y1 x2 y2
-2-7/2-5=m
-9/-3=m
Simplifies to
3=m
the formula s= I dont know how to type that but I really need helppppp

Answers
Answer:
\( s = \sqrt{30} - 2\sqrt{5} m \)
Step-by-step explanation:
Given:
Formula for side length of cube, \( s = \sqrt{\frac{SA}{6} \)
Where, S.A = surface area of a cube, and s = side length.
Required:
Difference in side length between a cube with S.A of 180 m² and a cube with S.A of 120 m²
Solution:
Difference = (side length of cube with 180 m² S.A) - (side length of cube with 120 m² S.A)
\(s = (\sqrt{\frac{180}{6}}) - (\sqrt{\frac{120}{6}})\)
\( s = (\sqrt{30}) - (\sqrt{20}) \)
\( s = \sqrt{30} - \sqrt{4*5} \)
\( s = \sqrt{30} - 2\sqrt{5} m \)
Determine whether 548 is greater than or less than 373. Then write the expression showing this using < or >.
Answers
Answer:
548 > 373
Step-by-step explanation:
548 is greater than 373 because when we compare the digits from left to right, we find that the first digit of 548 (5) is greater than the first digit of 373 (3). Therefore, we can conclude that 548 is greater than 373.
The ">" symbol is used to represent "greater than" in mathematical comparisons.
Hope this helps!
What is the solution of ?\(\frac{5}{2} x-7=\frac{3}{4} x+14\)
Answers
Combine the terms by multiplying into a single fraction.
\(\bf{\dfrac{5}{2}x-7=\dfrac{3}{4}x+14 }\)
Find the common denominator.
\(\bf{\dfrac{5x}{2}-7=\dfrac{3}{4}x+14 }\)
Combine fractions with the lowest common denominator.
\(\bf{\dfrac{5x(-7)}{2}=\dfrac{3}{4}x+14 }\)
Multiply the numbers.
\(\bf{\dfrac{5x-14}{2}=\dfrac{3}{4}x+14 }\)
Combine the multiplied terms into a single fraction
\(\bf{\dfrac{5x-14}{2}=\dfrac{3x}{4}+14 }\)
Find the common denominator.
\(\bf{\dfrac{5x-14}{2}=\dfrac{3x}{4}+\dfrac{4\cdot14}{4} }\)
Combine fractions with the lowest common denominator.
\(\bf{\dfrac{5x-14}{2}=\dfrac{3x+4\cdot14}{4} }\)
Multiply the numbers.
\(\bf{\dfrac{5x-14}{2}=\dfrac{3x+56}{4} }\)
Eliminate the denominators of the fractions.
\(\bf{4\cdot\dfrac{5x-14}{2}=4\cdot\dfrac{3x+56}{4} }\)
Cancel the multiplied terms that are in the denominator.
\(\bf{2(5x-14)=3x+56}\)
To distribute.
\(\bf{10x-28=3x+56 }\)
Add 28 to both sides.
\(\bf{10x-28+28=3x+56+28 }\)
Simplify
\(\bf{10x=3x+84 }\)
Subtract 3x from both sides.
\(\bf{10x-3x=3x+84-3x }\)
Simplify
\(\bf{7x=84 }\)
Divide both sides by the same factor.
\(\bf{x=\dfrac{84}{7} }\)
Simplify
\(\bf{x=12 \ \ \ === > \ \ \ Answer}\)
↓
VerificationLet x=12.
\(\bf{\dfrac{5}{2}\times12-7=\dfrac{3}{4}\times12+14 }\)\(\bf{\dfrac{5\times12}{2}-7=\dfrac{3}{4}\times12+14 }\)\(\bf{\dfrac{60}{2}-7=\dfrac{3}{4}\times12+14 }\)\(\bf{30-7=\dfrac{3}{4}\times12+14 }\)\(\bf{30-7=\dfrac{3\times12}{4}+14 }\)\(\bf{30-7=\dfrac{36}{4}+14 }\)\(\bf{30-7=9+14 }\)\(\bf{23=9+14 }\)\(\bf{23=23}\)Checked ✅
The product of two consecutive positive even number is 48. Find the number using factorization method solve
x²-2x-4 = 0
Answers
Answer:
View the image attached

is 4/5 greater than or less than 2/3?
Answers
Answer:
Yes 4/5 is greater than 2/3
Step-by-step explanation:
Because
4/5 = 0.8
2/3 = 0.667
Then, we compare the two decimal numbers to get the answer.
0.8 is greater than 0.667.
Therefore, 4/5 is greater than 2/3 and the answer to the question "Is 4/5 greater than 2/3?" is yes.
Select the correct answer from each drop-down menu. Graph shows a four-sided polygon is plotted on a coordinate plane at A (3, 4), B (5, 3), C (3, 2), and D (1, 3). Polygon ABCD is plotted on a coordinate plane. If the polygon translates 3 units to the left and 1 unit down, the length of diagonal A ′ C ′ ¯ is units. If the polygon translates 3 units further to the left and four units down, the length of diagonal A ′ C ′ ¯ . Reset Next
Answers
Therefore, the length of diagonal A'C' is also 2 units after the polygon translates 3 units further to the left and 4 units down.
What is a polygonal example?A polygon is any form having three sides. Although a circle is curved and devoid of sides and angles, it is not categorised as a polygon even if it is a plane figure.
If the polygon translates 3 units to the left and 1 unit down, the coordinates of the new vertices would be:
A' (0, 3)
B' (2, 2)
C' (0, 1)
D' (-2, 2)
To find the length of diagonal AC, we can use the distance formula:
AC = √[(3-3)^2 + (2-4)^2] ≈ 2 units
If the polygon translates 3 units further to the left and 4 units down, the coordinates of the new vertices would be:
A'' (-3, -1)
B'' (-1, -2)
C'' (-3, -3)
D'' (-5, -2)
To find the length of diagonal A'C', we can use the distance formula:
A'C' = √[(0-0)^2 + (1-3)^2] ≈ 2 units
Therefore, the length of diagonal A'C' is also 2 units after the polygon translates 3 units further to the left and 4 units down.
To know more about polygon visit:
https://brainly.com/question/24464711
#SPJ1
What is the answer to this question in the picture

Answers
9514 1404 393
Answer:
\(\displaystyle\sqrt{x+7}-\log{(x+2)}\)
Step-by-step explanation:
It's pretty straightforward. You want ...
f(x) - g(x)
Substituting the given function definitions gives ...
\(\displaystyle\boxed{\sqrt{x+7}-\log{(x+2)}}\)
A college graduate expects to earn a salary of $55,000 during the first year after graduation and receive a 3% raise every year after that. What is the total income he will have received after ten years?
Answers
Answer:
$73915.40
Step-by-step explanation:
→ Find the multiplier
( 3 + 100 ) ÷ 100 = 1.03
→ Multiply by principal amount and raise it to the power of years
55000 × 1.03¹⁰ = 73915.40
Answer: $630,513.36
Step-by-step explanation:
Making a Formula for His Salary on a Given YearLet's make a table of values to see how much he earns every year after graduation.
1 year -> $55,000
2 years -> 55,000 * 103% = $56,650
3 years -> 56,650 * 103% = 55000 * 103% * 103% = $58,349.50
4 years -> 58349.50 * 103% = 55,000 * 103% * 103% * 103% = 55000(1.03)³
Here, we see that every year, he gets 103% of what he got the previous year, which is also 1.03 times his previous salary.
We also see that we multiply 55000 by 1.03 three times in the fourth year, and two times in the third year. This means that we multiply 55000 by 1.03 n-1 times.
Using this, let's generalize this for n.
n years -> \(55000(1.03)^{n-1}\)
Finding the Sum after Ten YearsWe are trying to find his total income after ten years, or the sum of his salary from year 1 to year 10. We can represent this in sigma notation like this
\(% Adjusted limits of summation$\displaystyle\sum_{n=1} ^{10} 55000(1.03)^{n-1}$\)
This essentially translates to the sum of the first ten terms in the sequence \(55000(1.03)^{n-1}\), starting at n=1.
Since this is a geometric sequence, or a sequence where we need to multiply by the same number to get to the next term, we can find the sum using the sum of geometric series formula. This formula is as follows:
\(S_n=a_1\frac{1-r^n}{1-r}\)
where \(S_n\) is the sum of the first n terms, \(a_1\) is the first term, r is the common ratio, and n is the number of terms. In this question, \(S_n\) is the total income after n years, \(a_1\) is his salary after the first year, r is how much his salary increases by each year, and n is the number of years we are calculating the sum for.
\(a_1\) -> 55000
r -> 1.03
n -> 10
Now that we have the values for each variable, let's plug them in and solve
\(S_{10}=55000(\frac{1-1.03^{10}}{1-1.03})\\S_{10}=630513.36\)
The total income he will have received after ten years is $630,513.36.
8=-2/5c what does c=
Answers
Answer:
c is -1/20
Step-by-step explanation:
sorry, i don't know how to get the answer
i literally typed it up
Perry is responsible for distributing soccer balls to the kids at soccer camp. During practice, Perry would like each group of 5 children to share two soccer balls. How many soccer balls does Perry need if 25 kids attend camp?
Answers
Q: Perry is responsible for distributing soccer balls to the kids at soccer camp. During practice, Perry would like each group of 5 children to share two soccer balls. How many soccer balls does Perry need if 25 kids attend camp?
A: 20 soccer balls
Hope this helped!
solve the equation.
x+(2)=5
Answers
Answer:
x = 3
Step-by-step explanation:
x+(2)=5
This is the same as x+2=5
To find x,
x + 2 = 5
-2 -2
This is to bring the 2 to the right hand side, leaving x
x = 3
The following picture shows a number line.
Each hash on the number line represents one unit. Which of the following statements is true?
A. The sum of points A, B, C, and D is greater than zero.
B. The sum of points B and C is greater than point A.
C. The sum of points A and B is greater than point C.
D. The opposite of point A is less than point D.
Show work here.

Answers
Answer:
We conclude that only option B is true.
i.e. The sum of points B and C is greater than point A
Step-by-step explanation:
Given the location of points on the left side of the number line
A=-6
B=-5
Given the location of points on the right side of the number line
C=3
D=4
Checking the statement A
The sum of points A, B, C, and D is greater than zero.
i.e. A+B+C+D > 0
-6 + -5 + 3 + 4 > 0
-11+7 > 0
-4 > 0
Thus,, this statement is false
Checking the statement B
The sum of points B and C is greater than point A
B+C>A
-5+3 > -6
-2 > -6
Thus, this statement is true.
Checking the statement C
The sum of points A and B is greater than point C
A+B > C
-6 + -5 > 3
-11 > 3
Thus, this statement is false
Checking the statement D
The opposite of point A is less than point D
As
A = -6
opposite of point A = -(-6)=6
The opposite of point A < D
6 < 4
Thus, this statement is false
Therefore, we conclude that only option B is true.
i.e. The sum of points B and C is greater than point A
NO LINKS!
The WBHS golf team was out hitting some golf balls on the weekend. Matt hit the ball off the ground and followed it a parabolic path reached a height of 4 feet. If ball hit the ground in 10 seconds, write the equation that would model the situation
h(t)=___(x - __)^2 + ___
Answers
========================================================
Explanation:
The instructions don't mention it, but I'm assuming that the height of 4 feet is the max height the of the ball.
If so, then this is the vertex of the parabola.
The ball is on the ground when x = 0 and x = 10. The x coordinate of the vertex is the midpoint of those two roots. So it's at x = 5.
Overall, the vertex is (h,k) = (5,4)
The equation
y = a(x-h)^2 + k
becomes
y = a(x-5)^2 + 4
Next, we plug in the root (x,y) = (10,0) since the ball hits the ground when x = 10. Let's solve for 'a'
y = a(x-5)^2 + 4
0 = a(10-5)^2 + 4
0 = 25a + 4
25a = -4
a = -4/25
We could have used (x,y) = (0,0) and we'd end up with the same 'a' value.
Therefore, the height function is
\(y = \boldsymbol{-\frac{4}{25}}(x - \boldsymbol{5})^2 + 4\)
Simplify; 25 3/8 - 15 1/4
A. 1/8
B. 10 2/32
C. 10 1/8
D. 10 1/2
Answers
Answer:
The choice C.
\(10 \frac{1}{8} \)
Step-by-step explanation:
\(25 \frac{3}{8} - 15 \frac{1}{4} \\ \\ \frac{203}{8} - \frac{61}{4} \\ \\ \frac{203}{8} - \frac{122}{8} = \frac{81}{8} = 10 \frac{1}{8} \)
=203/8 - 61/4
=203/8 - 122/8
=81/8
=10 1/8
Therefore the answer is C
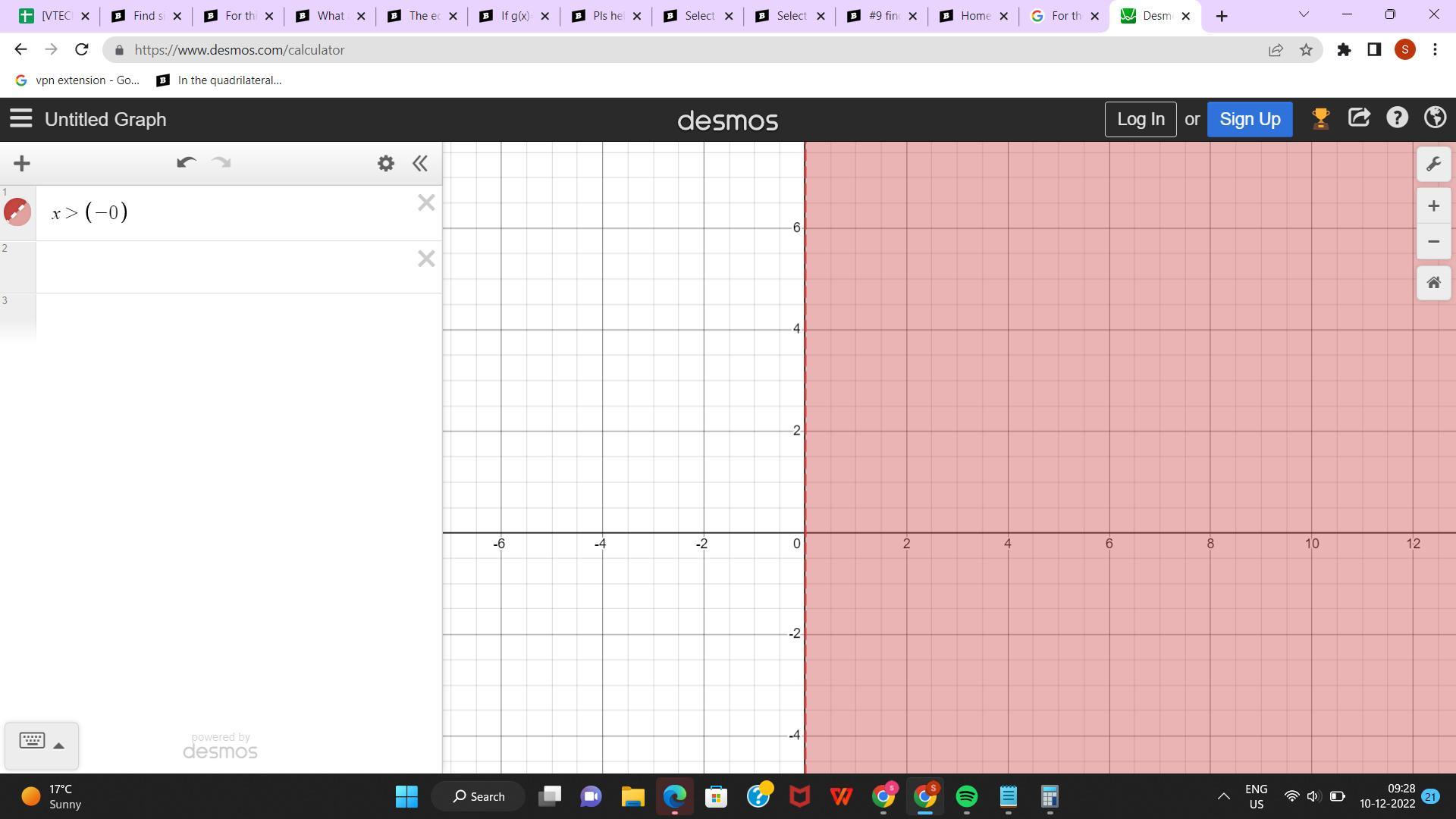
Select the graph for the solution of the open sentence. Click until the correct graph appears. |x| + 3 > 3
Answers
The graph for |x| + 3 > 3 is attached below.
What is open sentence?It is unknown if a mathematical sentence is true or false since it uses variables, which is known as a "open sentence" in mathematics. On the other hand, a closed sentence is a mathematical statement that is known to be either true or untrue.
Given:
|x| + 3 > 3
|x| > 3- 3
|x| > 0
Now, The open sentence is an absolute inequality, so we start by analyzing the inequality sign > 0 means that, the x-values of the inequality is not less than 0.
So, the shaded area of the graph are: x >0 then right side of the graph is shaded.
Learn more about open sentence here:
brainly.com/question/2448784
#SPJ1
pls help me i will mark brainliest if you are right !

Answers
Answer:
second option
Step-by-step explanation:
diameter= 22 cm
radius = diameter/2
=22/2
11 cm
volume of a sphere = \(\frac{4}{3}*pie* r^3\)
=\(\frac{4}{3} * 3.14 *11^3\)
=4.186666 * 1331
=5572 . 5 cubic centimeters (cm^3)
Area of Rectangles
Best answer marks branlist!

Answers
Answer:
rectangle above = 3 x 5 = 15 cm²
rectangle below = 8 x 5 = 40 cm²
functions please helpp

Answers
Answer:
Functions:
3. The chart with arrows
4. The graph
Not Functions:
1. (1,1), (2,2), (3,3), (1,4)
2. (1,17), (0,16), (0,15), (-2,17)
Step-by-step explanation:
Functions do not have repeating domains (x-coordinates).
Hope it helps!
Find each indicated measure for circle O.
M
MCE =
M
M
M
answer all pls :)

Answers
The indicated measures in the given circle are:
a. m<A = 38°; b. m(CE) = 56°; c. m<C = 38°; d. m<D = 39°;
e. m<ABE = 67°
How to Find Each Indicated Measure for the Circle?In order to find the indicated measures in the circle, recall that the measure of an inscribed angle is half of the measure of the intercepted arc based on the inscribed angle theorem.
Thus, we have:
a. m<A = 1/2(m(BD))
Substitute:
m<A = 1/2(76)
m<A = 38°
b. m(CE) = 2(m<CBE))
Substitute:
m(CE) = 2(28)
m(CE) = 56°
c. m<C = 1/2(m(BD))
Substitute:
m<C = 1/2(76)
m<C = 38°
d. m<D = 1/2(m(AC))
Substitute:
m<D = 1/2(78)
m<D = 39°
e. m<ABE = 1/2(m(ACE))
m<ABE = 1/2(m(AC) + m(CE))
Substitute:
m<ABE = 1/2(78 + 56)
m<ABE = 67°
Learn more about measures in a circle on:
https://brainly.com/question/24348931
#SPJ1
through -2, 3), whone
Answers
A soccer coach purchased one goal and some soccer balls for the team. The expression 180 + 15x represents the cost before tax. What do the different parts of the expression model? Drag the parts of the expression into the boxes to match each description. Put responses in the correct input to answer the question. Select a response, navigate to the desired input and insert the response. Responses can be selected and inserted using the space bar, enter key, left mouse button or touchpad. Responses can also be moved by dragging with a mouse. cost of goal total cost of soccer balls
Answers
The meaning of the terms and factors in the expression are
180 ⇒ cost of goal15x ⇒ total cost of soccer ballsx ⇒ Number of soccer balls180 + 15x ⇒ total cost of soccer balls and goalHow to determine what the different parts of the expression model represents?The expression is given as
180 + 15x
The above expression can be split as follows:
180 15xx180 + 15xThe meaning of the above terms and factors are
180 ⇒ cost of goal15x ⇒ total cost of soccer ballsx ⇒ Number of soccer balls180 + 15x ⇒ total cost of soccer balls and goalRead more about linear functions at
https://brainly.com/question/4025726
#SPJ1
A right triangle has side lengths that are consecutive integers and a perimeter of 12 feet. What are the
angles of the triangle?
А. 30°, 60° and 90°
B. 33.47°, 56.53° and 90°
C. 36.87°, 53.13° and 90°
D. 40.16°, 49.84° and 90°
Answers
Answer:
option c
Step-by-step explanation:
Let the sides of the right angled triangle = x , (x +1) , (x +2)
Perimeter = 12 feet
x + x +1 + x + 2 = 12
x +x + x + 1+2 = 12
Combine like terms
3x+ 3 = 12
Subtract 3 from both sides
3x = 12- 3
3x = 9
Divide both sides by 3
x = 9/3
x = 3
x + 1 = 3 + 1 = 4
x + 2 = 3 + 2 = 5
The sides of the triangle are 3 , 4 ,5
The biggest side will be the hypotenuse.
So, hypotenuse = 5 ft. other legs are 3 and 4
\(\text {Sin \ $\theta$ = $\dfrac{opposite \ side \ of \ \theta}{hypotenuse}$ } \\\\\\ = \dfrac{4}{5}\\\\\\Sin \ \theta = 0.8\\\\\theta = Sin^{-1} \ 0.8\\\\\theta = 53.13 \ ^\circ\)
another angle = 180 - [ 90 + 53.13]
= 180 - 143.13
= 36.87°
whatz is avagadro no.
Answers
Find the area of the triangle having the indicated angle and sides. (Round your answer to one decimal place.)
B 128°, a 86, c = 37

Answers
The area of the triangle with angle B = 128°, side a = 86, and side c = 37 is approximately 2302.7 square units.
To find the area of a triangle when one angle and two sides are given, we can use the formula for the area of a triangle:
Area = (1/2) * a * b * sin(C),
where a and b are the lengths of the two sides adjacent to the given angle C.
In this case, we have angle B = 128°, side a = 86, and side c = 37. To find side b, we can use the law of cosines:
c² = a² + b² - 2ab * cos(C),
where C is the angle opposite side c. Rearranging the formula, we have:
b² = a² + c² - 2ac * cos(C),
b² = 86² + 37² - 2 * 86 * 37 * cos(128°).
By substituting the given values and calculating, we find b ≈ 63.8.
Now, we can calculate the area using the formula:
Area = (1/2) * a * b * sin(C),
Area = (1/2) * 86 * 63.8 * sin(128°).
By substituting the values and calculating, we find the area of the triangle to be approximately 2302.7 square units.
For more question on area visit:
https://brainly.com/question/2607596
#SPJ8
Can someone please provide a step-by-step explanation for the answer?
If the universe of discourse is the real numbers, give the truth value of each of the
following propositions:
(a) ∀x∃y(x = y²)
(b) ∀x∃y(x² = y)
(c) ∃x∀y(xy = 0)
(d) ∀x∃y(x + y = 1)

Answers
The Propositions are resulting
(a) ∀x∃y(x = y²) is False
(b) ∀x∃y(x² = y) is True.
(c) ∃x∀y(xy = 0) is True.
(d) ∀x∃y(x + y = 1) is True.
(a) ∀x∃y(x = y²)
This proposition states that for every x, there exists a y such that x is equal to y². To determine the truth value, we need to check if this statement holds true for every value of x.
If we take any positive value for x, we can find a corresponding value of y that satisfies the equation.
For example, if x = 4, then y = 2 satisfies the equation since 4 = 2². Similarly, if x = 9, then y = 3 satisfies the equation since 9 = 3².
Therefore, the proposition (a) is false.
(b) ∀x∃y(x² = y)
For any given positive or negative value of x, we can find a corresponding value of y that satisfies the equation.
For example, if x = 4, then y = 2 satisfies the equation since 4² = 2. Similarly, if x = -4, then y = -2 satisfies the equation since (-4)² = -2.
Therefore, the proposition (b) is true.
(c) ∃x∀y(xy = 0)
The equation xy = 0 can only be satisfied if x = 0, regardless of the value of y. Therefore, there exists an x (x = 0) that makes the equation true for every y.
Therefore, the proposition (c) is true.
(d) ∀x∃y(x + y = 1)
To determine the truth value, we need to check if this statement holds true for every value of x.
If we take any value of x, we can find a corresponding value of y that satisfies the equation.
For example, if x = 2, then y = -1 satisfies the equation since 2 + (-1) = 1. Similarly, if x = 0, then y = 1 satisfies the equation since 0 + 1 = 1.
Therefore, the proposition (d) is true.
Learn more about Proposition here:
https://brainly.com/question/30695879
#SPJ1