In which year did Eugene, Oregon have the greatest difference between high and low temperatures in November?
A)November 2009
B)November 2010
C)November 2011
D)November 2008

Answers
Related Questions
A tabletop in the shape of a trapezoid has an area of 5,700 square centimeters. its longer base measures 135 centimeters, and the shorter base is 105 centimeters. what is the height? the height of the tabletop is centimeters.
Answers
Answer:
47.5 cm
Step-by-step explanation:
You want the height of a trapezoid with bases of lengths 135 cm and 105 cm, and an area of 5700 cm².
AreaThe formula for the area of a trapezoid is ...
A = 1/2(b1 +b2)h
Filling in the given values, we have ...
5700 = 1/2(135 +105)h
5700 = 120h
h = 5700/120 = 47.5
The height of the tabletop is 47.5 cm.
<95141404393>
Select the real-world problem that could be solved using a proportion.

Answers
the answer is D
300/6 = x/10
once solved, it will be proportional
There are 23 families living in the Willbrook Farms Development. Of these families, 11 prepared their own federal income taxes for last year, Six had their taxes prepared by a local professional, and the remaining Six by H&R Block.
a. What is the probability of selecting a family that prepared their own taxes?
b. What is the probability of selecting two families, both of which prepared their own taxes?
c. What is the probability of selecting three families, all of which prepared their own taxes?
d. What is the probability of selecting two families, neither of which had their taxes prepared by H&R Block?
Answers
The probability of selecting a family that prepared their own taxes is approximately 0.478, or 47.8%.
The probability of selecting two families, both of which prepared their own taxes, is approximately 0.221, or 22.1%.
The probability of selecting three families, all of which prepared their own taxes, is approximately 0.098, or 9.8%.
The probability of selecting two families, neither of which had their taxes prepared by H&R Block, is approximately 0.520, or 52.0%.
Here, we have,
a. The probability of selecting a family that prepared their own taxes can be calculated by dividing the number of families that prepared their own taxes (11) by the total number of families (23):
P(family prepared own taxes) = 11/23 = 0.478
There are 11 families that prepared their own taxes out of a total of 23 families.
The probability of selecting a family that prepared their own taxes is approximately 0.478, or 47.8%.
b. The probability of selecting two families, both of which prepared their own taxes, can be calculated by multiplying the probability of selecting the first family that prepared their own taxes (11/23) by the probability of selecting the second family from the remaining families that also prepared their own taxes:
P(both families prepared own taxes) = (11/23) * (10/22) = 0.221
The probability of selecting the first family that prepared their own taxes is 11/23. After selecting the first family, there are 10 families left that prepared their own taxes out of the remaining 22 families.
The probability of selecting two families, both of which prepared their own taxes, is approximately 0.221, or 22.1%.
c. The probability of selecting three families, all of which prepared their own taxes, can be calculated by multiplying the probability of selecting the first family that prepared their own taxes (11/23) by the probability of selecting the second family from the remaining families that prepared their own taxes (10/22), and then multiplying by the probability of selecting the third family from the remaining families that prepared their own taxes (9/21):
P(all families prepared own taxes) = (11/23) * (10/22) * (9/21) ≈ 0.098
The probability of selecting the first family that prepared their own taxes is 11/23. After selecting the first family, there are 10 families left that prepared their own taxes out of the remaining 22 families. Similarly, after selecting the second family, there are 9 families left that prepared their own taxes out of the remaining 21 families.
The probability of selecting three families, all of which prepared their own taxes, is approximately 0.098, or 9.8%.
d. The probability of selecting two families, neither of which had their taxes prepared by H&R Block, can be calculated by multiplying the probability of selecting the first family that did not have their taxes prepared by H&R Block (17/23) by the probability of selecting the second family from the remaining families that also did not have their taxes prepared by H&R Block (16/22):
P(neither family had taxes prepared by H&R Block) = (17/23) * (16/22) ≈ 0.520
The probability of selecting the first family that did not have their taxes prepared by H&R Block is 17/23. After selecting the first family, there are 16 families left that did not have their taxes prepared by H&R Block out of the remaining 22 families.
The probability of selecting two families, neither of which had their taxes prepared by H&R Block, is approximately 0.520, or 52.0%.
To know more about probability , visit;
brainly.com/question/32004014
#SPJ4
X -2/5=7 help please
Answers
Answer:
37
Step-by-step explanation:
Here is a set of signed numbers: 7, -3, LaTeX: \frac{1}{2}1 2, -0.8, 0.8, LaTeX: -\frac{1}{10}− 1 10, -2 Order the numbers from least to greatest. Group of answer choices 7, 0.8, 1/2, -1/10, -0.8, -2, -3 -3, -2, -0.8, -1/10, 1/2, 0.8, 7 -1/10, 1/2, -0.8, 0.8, -2, -3, 7
Answers
Answer:
\(-3, -2, -0.8, -\frac{1}{10} ,\frac{1}{2}, 0.8, 7\)
Step-by-step explanation:
Given
\(7, -3, \frac{1}{2}, -0.8, 0.8, -\frac{1}{10}, -2\)
Required
Order from least to greatest
\(7, -3, \frac{1}{2}, -0.8, 0.8, -\frac{1}{10}, -2\)
Convert 1/2 and -1/10 to decimals
\(7, -3, 0.5, -0.8, 0.8, -0.1, -2\)
Negative numbers are always the least of all numbers.
In the given list, the negative numbers are:
\(-3, -0.8, -0.1, -2\)
The higher the magnitude of a negative number, the smaller it is.
--------------------------------------------------------------------------------------------
Take for instance: -7 and -8.
-8 has a magnitude of 8 and -7 has a magnitude of 7.
Because 8 > 7 (the magnitudes), then
-8 < -7
--------------------------------------------------------------------------------------------
Using the above analysis:
\(-3, -0.8, -0.1, -2\) from least to greatest is:
\(-3, -2, -0.8, -0.1\)
Considering the positive numbers:
\(7, 0.5, 0.8\)
From least to greatest, it is:
\(0.5, 0.8, 7\)
Merge the negative and the positive numbers:
\(-3, -2, -0.8, -0.1,0.5, 0.8, 7\)
Convert 0.5 and -0.1 back to fractions
\(-3, -2, -0.8, -\frac{1}{10} ,\frac{1}{2}, 0.8, 7\)
Select the clause from the drop-down menu to correctly complete the sentence.
Be sure to wear goggles while you swim
Choose...
..thar last word is chlorine by the way
Answers
Answer: ;otherwise, your eyes will become very irritated from the chlorine.
Step-by-step explanation: I took the test
Answer:
the answer above is right i jus took the test
Step-by-step explanation:
I need help with this question

Answers
The length of the legs of the right triangle are 2.83 units.
How to find the side of a right triangle?A right tangle triangle is a triangle that has one of its angles as 90 degrees. The sum of angles in a triangle is 180 degrees.
Therefore, the legs of the triangle can be found using trigonometric ratios.
Hence,
sin 45 = opposite / hypotenuse
sin 45 = a / 4
cross multiply
a = 4 × 0.70710678118
a = 2.83 units
Therefore,
cos 45 = b / 4
cross multiply
b = 0.70710678118 × 4
b = 2.82842712475
b = 2.83 units
Therefore, the legs are 2,83 units
learn more on right triangle here: https://brainly.com/question/29285631
#SPJ1
Can any kind soul help me ASAP!

Answers
Answer:
the answer is B
x = 1
Step-by-step explanation:
the symmetry is in the middle of the curve like a mirror and the equation of the mirror or symmetry line is x=1
hi!!!! could someone please help im the middle of taking a test

Answers
Answer:
126
might be the answer
You can Check by counting the box
the angle of elevation of the top of a tower from a point 42 metres away from it's base on level ground is 26 degrees. find the height of the tower.
Answers
Answer:
20.485 Meters
Step-by-step explanation:
So first you wanna draw a diagram. Start with the tower, then on the ground to the left (or right) draw a point. The point will be labeled as 42 m away from the tower. Now draw a line from that point to the top of the tower. This makes your triangle, and that angle you just drew that touches the point is 26 degrees.
Now, since you have a right triangle you can use trig. You know an angle and a side. Specifically, relative to the 26 degree angle you know the adjacent angle and want the opposite, which is the tower. So opposite and adjacent is tangent. So you set up tan(26) = o/42 where o is the opposite side.
So solving you get o = 20.485 meters
6. bryce played the same song on guitar hero 8 times and scored the following percentages for his accuracy: 89%,82%,90%,88%,89%,91%,85%, and95% based on his scores, he wants to know the population mean that he will score a90%or better. which would be the best estimate? 0.5 0.625 0.25 0.375
Answers
The best estimate for the population mean that Bryce will score a 90% or better is 0.625.
Based on the given information, Bryce played the same song on Guitar Hero 8 times and scored percentages of 89%, 82%, 90%, 88%, 89%, 91%, 85%, and 95%. He wants to know the population mean that he will score a 90% or better. Which would be the best estimate?
To find the population mean, we need to calculate the average of Bryce's scores.
Step 1: Add up all the scores: 89 + 82 + 90 + 88 + 89 + 91 + 85 + 95 = 709.
Step 2: Divide the sum by the total number of scores (8): 709 / 8 = 88.625.
Therefore, the best estimate for the population mean that Bryce will score a 90% or better is 0.625.
To know more about population mean refer here:
https://brainly.com/question/33439013
#SPJ11
Kill’em Dead Pest Control needs to set out 5 roach motels per square yard. In a rectangular studio apartment that’s 7 yards by 4 yards wide, about how many roach motels will need to be set out?
Answers
Answer:
113 moteis
Step-by-step explanation:
A = 7 x 4 = 28 yards^2
1 yard - 0,9 m
1 yard^2 - 0,81 m^2
28 yards^2 - A
A = 28 x 0,81 = 22,68m^2
22,68 x 5 = 113,4
113 moteis
Answer:
140
Step-by-step explanation:
because it is
PLEASE HELP ASAP FOR ALGEBRA 1 Mr Reder has just robbed a bank and is trying to escape on foot. He is currently 3 miles from the bank and running at 5 miles per hour. Write an equation to model how far from the bank Mr Reder is after a certain amount of time has passed. How far has he gone after 3 hours? Draw an appropriate graph for this equation.
Answers
Answer:
He has ran 15 miles and passed the bank 12 miles from his location where he is at.
Step-by-step explanation:
WHY WAS HE ROBBING A BANK?????????
Answer:
Step-by-step explanation:
His distance from the bank can be modeled using an equation in the form y=mx+b. Since he has already ran 3 miles, the "b" is equal to 3, and can be added to how many miles he runs on from now on. If he can run 5 miles per hour, then that means every hour, he will run 5 miles. We can represent how many hours have passed as x. This would make our equation y=5x+3.
After 3 hours he has gone 5(3)+3 miles, or 18 miles

A test is worth 50 points. Multiple-choice questions are worth 1 point, and
short-answer questions are worth 3 points. If the test has 20 questions, how
many multiple-choice questions are there?
A. m + s = 50
B. m + 2s = 20
C. m.s= 20
D. m + s = 20
Answers
Answer:
d) m + s = 20
m = 5
Step-by-step explanation:
m + 3s = 50
m + s = 20
m + 3(20-m) = 50
m + 60 - 3m = 50
60 - 2m = 50
60 = 50 + 2m
60 - 50 = 2m
10 = 2m
5 = m
What is the slope of a line perpendicular to the line whose equation is 3x+y=8. Fully simplify your answer.
Answers
Phones-R-Us charges $16.95 per
month and $0.05 per text message.
Awesome Wireless charges $22.95 per
month and $0.02 per text message.
During one month, how many text
messages can be sent so that
Awesome Wireless cost greater than
or equal to Phones-R-Us?
Answers
Answer:
874.5 text messagesStep-by-step explanation:
To solve this problem let us find out how many text messages can be sent from both phones
1. Phones-R-Us
total charges= $16.95
cost per text message= $0.05
number of text message= 16.95/0.05
=339 messages
2. Awesome wireless
total charges= $22.95
cost per text message= $0.02
number of text message= 22.95/0.02
=1147.5messages
Now if Awesome wireless to equal Phones-R-Us then the number of sms would be
16.95/0.02
=874.5 text messages
Find the length of the third side. If necessary, write in simplest radical form.

Answers
Answer:
6
Step-by-step explanation:
The value of the square length of the hypotenuse is equal to sum of the square length of the two legs: let x represent the missing side
\(\sqrt{} 85^{2}\) = 7^2 + x^2 calculate the powers
85 = 49 + x^2 subtract 49 from both sides
36 = x^2 find the root of the both sides
6 = x
solve the separable differential equation 9x−4yx2 1−−−−−√dydx=0. subject to the initial condition: y(0)=4.
Answers
The solution to the differential equation with the given initial condition is y = (√(\(x^2 + 1\)) - 3x) / 2.
We can separate the variables and integrate both sides as follows:
∫ 1/(9x - 4y√(\(x^2 + 1\))) dy = ∫ dx
Let u = \(x^2 + 1\), then du/dx = 2x and we have:
∫ 1/(9x - 4y√(\(x^2 + 1\))) dy = ∫ 1/u * (du/dx) dy
∫ 1/(9x - 4y√(\(x^2 + 1\))) dy = ∫ 2x/(\(9x^2 - 4y^2u\)) du
We can now integrate both sides with respect to their respective variables:
(1/4)ln|9x - 4y√(\(x^2\) + 1)| + C1 = ln|u| + C2
(1/4)ln|9x - 4y√(\(x^2\) + 1)| + C1 = ln|x^2 + 1| + C2
where C1 and C2 are constants of integration.
Using the initial condition y(0) = 4, we can substitute x = 0 and y = 4 into the above equation to solve for C1 and C2:
(1/4)ln|36| + C1 = ln|1| + C2
C1 = C2 - (1/4)ln(36)
Substituting this into the above equation, we get:
(1/4)ln|9x - 4y√(\(x^2 + 1\))| = ln|\(x^2 + 1\)| - (1/4)ln(36)
Taking the exponential of both sides, we get:
|9x - 4y√(\(x^2 + 1)|^{(1/4)\) = |\(x^2 + 1|^{(1/4)\) / 6
Squaring both sides and simplifying, we get:
y = (√(\(x^2 + 1\)) - 3x) / 2
To know more about differential equation, refer to the link below:
https://brainly.com/question/15168689#
#SPJ11
Polygon CCC has an area of 404040 square units. K 2ennan drew a scaled version of Polygon CCC using a scale factor of \dfrac12 1 2 start fraction, 1, divided by, 2, end fraction and labeled it Polygon DDD. What is the area of Polygon DDD?
Answers
Answer:
Area of polygon D = 10 square units
Step-by-step explanation:
Given:
Polygon C has an area of 40 square units.
It is scaled with a scale factor of \(\frac{1}2\) to form a new polygon D.
To find:
The area of polygon D = ?
Solution:
When any polygon is scaled to half, then all the sides of new polygon are half of the original polygon.
And the area becomes one-fourth of the original polygon.
Let us consider this by taking examples:
First of all, let us consider a right angled triangle with sides 6, 8 and 10 units.Area of a right angled triangle is given by:
\(A = \dfrac{1}{2} \times Base \times Height\\\Rightarrow A = \dfrac{1}{2} \times 6 \times 8 = 24\ sq\ units\)
If scaled with a factor \(\frac{1}{2}\), the sides will be 3, 4 and 5.
New area, A':
\(A' =\dfrac{1}{2} \times 3 \times 4 = 6\ sq\ units = \dfrac{1}4\times A\)
i.e. Area becomes one fourth.
Let us consider a rectangle now.Sides be 8 and 10 units.
Area of a rectangle, A = \(Length \times Width\) = 8 \(\times\) 10 = 80 sq units.
Now after scaling, the sides will be 4 and 5 units.
New Area, A' = 4 \(\times\) 5 =20 sq units
So, \(\bold{A' = \frac{1}4 \times A}\)
Now, we can apply the same in the given question.
\(\therefore\) Area of polygon D = \(\bold{\frac{1}{4}}\)\(\times\) Area of polygon C
Area of polygon D = \(\bold{\frac{1}{4}}\)\(\times\) 40 = 10 sq units
Answer:
Step-by-step explanation:
10
The annual profits for a company are given in the following table, where x represents the number of years since 2006, and y represents the profit in thousands of dollars. Write the linear regression equation that represents this set of data, rounding all coefficients to the nearest hundredth. Using this equation, find the projected profit (in thousands of dollars) for 2015, rounded to the nearest thousand dollars.
Regression equation:
Final answer in thousand dollars:

Answers
Answer: Hello how are you doing today?
Step-by-step explanation: How may I help you?
2020-21
19 of 35
Text-to-Speech
19. Brian bought a new jacket at a discount of 30%. If the original price was $65, how
much did Brian pay for the jacket?
Answers
Answer: Brain paid $ 45.5 for the jacket.
Step-by-step explanation:
Given: Original price of jacket = $ 65
Discount -= 30%
Price after discount = Original price - 30% of Original price
= 65 - 30% of 65
= 65 - (0.3) x 65 [30% = 0.3]
= (65) (1-0.3 ) [Taking 65 common]
= (65)(0.7)
= $ 45.5
Hence, Brain paid $ 45.5 for the jacket.
im stuck pls help me 6

Answers
Answer:
6)a. π(16²)x = 62,731.3
b.
\(x = \frac{62731.3}{\pi( {16}^{2} )} = 78\)
c. The height is 78 cm.
The tens digit of a two-digit number is twice the ones digit. Its reversed number is 36 less than the original number.
Answers
From the calculation, the original number is obtained as 84.
What is the original number?We know that we are told in the question that in the question, we are required to obtain the number and that is what we are going to do below.
Let the tens digit be T and let the units digit be U
We can then write
10U+T = 10T+U-36
Since the reversed number is 36 less than the original number.
Then;
9U = 9T -36
Dividing both sides of the equation by 9
U = T -4
U=2U-4
U=4
T = 8
It then follows that the original number is 84.
Learn more about tens digit:https://brainly.com/question/13722748
#SPJ1
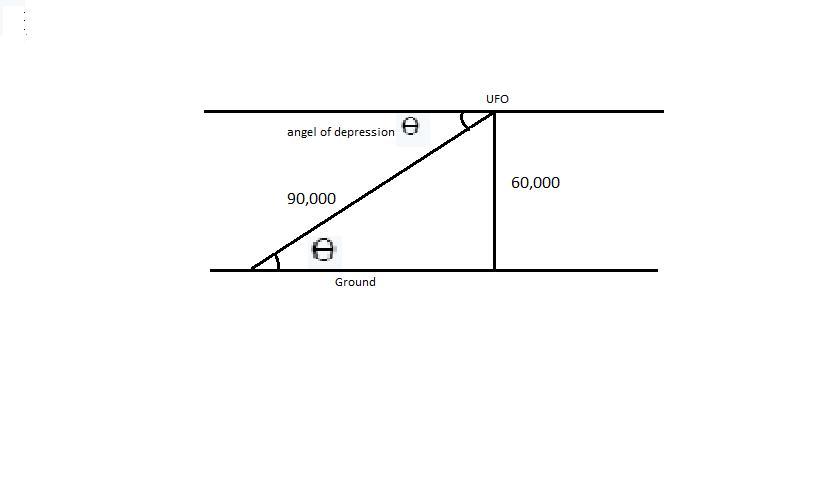
A UFO is coming in to pick up some test subjects. Their elevation above the ground is 60,000 feet. Their laser sights tell them that a direct (diagonal) path to the nearest landing area is 90,000 feet away. What is the angle of depression as they come in to land?
Answers
Answer:
41.83°
Step-by-step explanation:
It is given that :
The vertical distance of the UFO from the ground = 60,000 feet
The diagonal distance of the landing area to the UFO = 90,000 feet
In order to find the angle of depression, we have to use the trigonometric ratios, i.e.,
\($\sin \ \theta = \frac{\text{perpendicular distance}}{\text{hypotenus}}$\)
\($\sin \ \theta = \frac{60,000}{90,000}$\)
\($\sin \ \theta = \frac{2}{3}$\)
\($\sin \ \theta = 0.667$\)
∴ \($\theta = \sin^{-1 }(0.667)$\)
= 41.83°
Can someone please help me ? I don’t understand this

Answers
What is the x-intercept of the following function?
h(x) = 4x+3 - 2
Answers
Answer:
Let h(x) = y
y = 4^(x+3) -2
For x intercept let y = 0
2 = 4^(x+3)
2= 2^2(x+3)
1 = 2x +6
2x = -5
2x = -5
Divide by 2
x = -5/2
The x intercept for the function is ( -5/2, 0)
Hope this helps.
Answer:
(-2.5,0)
Step-by-step explanation:
\(h(x)=4^{x+3}-2\)
Since the x intercept of a graph is when the y value is 0:
\(0=4^{x+3}-2 \\\\2=4^{x+3} \\\\2=(2^2)^{x+3} \\\\2^1=2^{2x+6} \\\\1=2x+6 \\\\2x=-5 \\\\x=-2.5\)
Hope this helps!
Find how many quarts of 6% butterfat milk and 2% butterfat milk should be mixed to yield 80 quarts of 5% butterfat milk.
Answers
If you mix x quarts of 6% butterfat milk with y quarts of 2% butterfat milk, then the resulting mixture would have a total volume of x + y quarts.
1 quart of the 6% milk contains 0.06 quart of fat, and 1 quart of the 2% contains 0.02 quart of fat. So x quarts of 6% milk contains 0.06x quart and y quarts of 2% milk contains 0.02y quart of fat, and the resulting mixture would contain a total of (0.06x + 0.02y) quarts of fat.
You want to end up with 80 quarts of 5% milk, which contains 0.05 • 80 quarts = 4 quarts of fat, so that
x + y = 80
0.06x + 0.02y = 4
Solve for x and y :
y = 80 - x
0.06x + 0.02 (80 - x) = 4
0.06x + 1.6 - 0.02x = 4
0.04x = 2.4
x = 60
y = 20
Can someone help with this?

Answers
Answer:
4 < n < 130.
Step-by-step explanation:
n is a positive integer
n^100 > 2^200
2^2*100 = 2^200
4 ^100 = 2^200
So n > 4
(130n)^50 > n^100
130^50 * n^50 > n^100
130^50 > n^50
130 >n
so n < 130.
Dennis made an extra 245. 00 do for selling furniture was 7% of the total value of the furniture he sold. What was the total value of the furniture Dennise sold?
Answers
The total value of the furniture that was sold by Dennis is 3,500 dollars.
What is the percentage?
The amount of something is expressed as if it is a part of the total which is a hundred. The ratio can be expressed as a fraction of 100. The word percent means per 100. It is represented by the symbol ‘%’.
Dennis made an extra $245.00 for selling furniture.
Let the cost of the furniture be x.
Let the total value of the furniture be x + 245.
The extra $245.00 was 7% of the total value of the furniture he sold.
0.07(x + 245) = 245
x+ 245 = 3500
x = 3255
Then the total value of the furniture is (3,255 + 245 =) $3,500.
Hope it helped!
6. suppose that x is an exponential random variable with mean 1. give another random variable that is negatively correlated with x and that is also exponential with mean 1.
Answers
If we let Z = 3 - X, then Z is another exponential random variable with mean 1 that is negatively correlated with X.
Let Y = 2 - X, where X is an exponential random variable with mean 1.
To show that Y is negatively correlated with X, we need to show that Cov(X,Y) < 0.
Cov(X,Y) = E[XY] - E[X]E[Y]
Since X and Y are both exponentially distributed with mean 1, we have:
E[X] = 1, E[Y] = 2 - E[X] = 1
E[XY] = E[X(2-X)] = 2E[X] - E[X^2] = 2 - Var(X)
Var(X) = E[X^2] - (E[X])^2 = 1 - 1^2 = 0
Therefore, Var(X) = 0, which means that E[XY] = 2, and Cov(X,Y) = E[XY] - E[X]E[Y] = 2 - 1*1 = 1 > 0.
Since Cov(X,Y) > 0, we know that Y is positively correlated with X. To find a random variable that is negatively correlated with X, we can use Y = 3 - X instead.
Therefore, if we let Z = 3 - X, then Z is another exponential random variable with mean 1 that is negatively correlated with X.
Learn more about variable here:
https://brainly.com/question/29696241
#SPJ11