(In(n)) 14 Consider the following series 72 What test(s) is(are) applicable to test the convergence or divergence of this series. Root test Ingegral test Geometric series test Ratio test (m) Does this series converge? No Yes
Answers
The series (In(n))^14 diverges. The series in question is (In(n))^14. To test for convergence or divergence, we can use the integral test since the series is a function of a continuous, positive, and decreasing function, ln(x).
To apply the integral test, we need to take the integral of the function (In(x))^14 from 1 to infinity:
∫[1, ∞] (In(x))^14 dx
We can use integration by parts, setting u = (In(x))^14 and dv = dx, to get:
∫[1, ∞] (In(x))^14 dx = (1/15) x (In(x))^15 - ∫[1, ∞] (1/15) x (In(x))^14 / x dx
Simplifying and evaluating the definite integral from 1 to infinity, we get:
∫[1, ∞] (In(x))^14 dx = (1/15) lim x→∞ [x (In(x))^15 - x] + (1/15)
Since the limit as x approaches infinity of x (In(x))^15 goes to infinity faster than x, the first term in the limit evaluates to infinity, and thus the integral test fails to converge.
Therefore, the series (In(n))^14 diverges.
Learn more about series here:
brainly.com/question/30098029
#SPJ11
Related Questions
you start a savings account with $200 and save $300 each month. Write an explicit formula to represent the amount of money you invest into your savings account as an arithmetic sequence. How much money will you have invested after 12 months? HELP!!!
Answers
Answer:
a\(_{n}\) = 3500
Step-by-step explanation:
a\(_{n}\) = a + d (n - 1)
a = 200
d = 300
n = 12
a\(_{n}\) = 200 + 300 (12 - 1)
= 200 + 300 (11)
= 200 + 3300
a\(_{n}\) = 3500
PLEASE ANSWER ASAP!! WORTH 20 POINTS
A cab company charges a $4 boarding rate in addition to its meter which is $1.50 for every mile. Write a linear equation which models this. Use the equation to determine the total fare for a trip that is 2 miles, 3 miles and 5 miles.
Answers
Answer:
y = 1.50x+4
if x = 2
y = 7
if x = 3
y = 8.5
if x = 5
y = 11.5
Step-by-step explanation:
every mile(x) add 1.50 dollars to 4 dollars
calculate the vertex of h(t) = - 16t^2 + 24t + 300
Answers
Answer: (-0.75, 309)
Step-by-step explanation:
To find the vertex, first we will complete the square.
Given:
h(t) = - 16t² + 24t + 300
Factor out -16:
h(t) = -16(t² - 1.5t) + 300
Add and subtract \(\frac{b}{2} ^2\):
h(t) = -16(t² - 1.5t + 0.5625 - 0.5625) + 300
Regroup:
-16 * -0.5625 = 9; 9 + 300 = 309
h(t) = -16(t² - 1.5t + 0.5625) + 309
Factor:
h(t) = -16(t² - 1.5t + 0.5625) + 309
h(t) = -16(t - 0.75)² + 309
Now, this equation is in vertex form. The vertex is (h, k) in the form y = a(x - h)² + k, meaning that our vertex is;
(-0.75, 309)
I have also graphed this, see attached.

The sum of two numbers is 54.The smaller number is 22 less than the larger number.what are the numbers?
Answers
Answer:
x=16 y=38
Step-by-step explanation:
x+y=54.......equation 1
x=y-22........ equation 2
substitute
y-22+y=54
2y-22=54
2y=54+22
2y=76
y=76/2
y=38''
x=y-22
x=38-22
x=16''
[(0)/(1) Points ] DETAILS PREVIOU. Simplify the compound fractional expression (1+(1)/(x+8))/(1-(1)/(x+8))
Answers
The simplified the compound fractional expression (1+(1)/(x+8))/(1-(1)/(x+8)) is (x+9)/(x+7).
To simplify the compound fractional expression (1+(1)/(x+8))/(1-(1)/(x+8)), we can follow the following steps:
Step 1: Find the common denominator for the fractions in the numerator and denominator. In this case, the common denominator is (x+8).
Step 2: Multiply the numerator and denominator of the expression by the common denominator to get rid of the fractions. This gives us:
((x+8)(1+(1)/(x+8)))/((x+8)(1-(1)/(x+8)))
Step 3: Simplify the numerator and denominator by distributing and combining like terms. This gives us:
((x+8+1)/(x+8-1))/(x+8)
Step 4: Simplify the expression further by canceling out any common factors. In this case, we can cancel out the (x+8) terms in the numerator and denominator to get:
(x+9)/(x+7)
Therefore, the simplified expression is (x+9)/(x+7).
Learn more expression at https://brainly.com/question/29293479
#SPJ11
Instructions: Find the missing length indicated.
I NEED HELP, NO LINKS PLEASE
can you explain please

Answers
Answer:
136
Step-by-step explanation:
First you need to know that there are 2 triangles in the image.
One triangle (the smaller one) has sides that measure 119 (the side) and 56 (the bottom).
The other triangle (the bigger one) has sides that measure 119 + ? (the side) and 120 (the bottom).
Let's replace the 119 + ? with an x so that the entire side length of the big triangle measures x.
1. Make a proportion using ratios. For the ratios of each triangle, we can do side over bottom lengths and then set them equal to each other.
119 = x sides
56 120 bottoms
2. You can cross multiply, or just solve for x.
119*120= 14280
14280/56= 255
3. Then subtract the total length minus 119 to find the question mark
255 - 119 = 136
(x+5) (x+2) (x+a) = x3 +bx 2+ cx-30 work out values of a,b and c
Answers
Answer:
\(a=-3, b=-4, c=-11\)
Step-by-step explanation:
\((x+5)(x+2)(x+a)=(x^2+7x+10)(x+a)=x^3+x^2(a+7)+x(10+7a)+10a \\ \\ \therefore 10a=-30 \implies a=-3 \\ \\ \therefore x^3+4x^2-11x-30 \implies b=-4, c=-11\)
Helllpppppp me please

Answers
Answer:
The answer is 9 7/10
Step-by-step explanation:
hope this helps
Hello I got this wrong will you help me solve

Answers
Solve for y
\(4x+3y=-21\)Subtract 4x both sides
\(\begin{gathered} 4x+3y-4x=-21-4x \\ 3y=-21-4x \\ \end{gathered}\)Divide by 3 into both sides
\(\begin{gathered} \frac{3y}{3}=-\frac{21}{3}-\frac{4x}{3} \\ y=-7-\frac{4}{3}x \\ by\text{ reordering} \\ y=-\frac{4}{3}x-7 \end{gathered}\)Answer:
\(y=-\frac{4}{3}x-7\)Amazon sells 3 whatsits for $5. 20 and 11whatsits for $10. 40?a. Write a function expressing cost as a function of the number whatsitsb. How many whatsits can you get for $22. 75
Answers
(a) To express the cost as a function of the number of whatsits, we can use the information provided. Let's assume x represents the number of whatsits. From the given data, we can set up two equations:
3x = $5.20
11x = $10.40
To find the cost as a function of the number of whatsits, we can divide the total cost by the number of whatsits:
Cost(x) = Total cost / Number of whatsits
Solving the equations above, we find that the cost per whatsit is $5.20/3 and $10.40/11, respectively. Therefore, the function expressing cost as a function of the number of whatsits is:
Cost(x) = ($5.20/3) * x = $1.7333x
(b) To determine how many whatsits can be obtained for $22.75, we can set up an equation using the cost function:
Cost(x) = $1.7333x
We need to solve for x when the cost is equal to $22.75:
$1.7333x = $22.75
Dividing both sides of the equation by $1.7333, we find:
x = $22.75 / $1.7333
Calculating this, we find that approximately 13.121 whatsits can be obtained for $22.75.
Therefore, you can get approximately 13 whatsits for $22.75.
Learn more about the cost here: brainly.com/question/10795261
#SPJ11
Given the functions f(x) = 2x^4 and g(x) = 4 x 2^x, which of the following statements is true

Answers
The statement that correctly shows the relationship between both expressions is
f(2) > g(2)
how to find the true statementThe given equation is
f(x) = 2x⁴ and
g(x) = 4 x 2ˣ
plugging in 2 for x in both expressions
f(x) = 2x⁴
f(2) = 2 * (2)⁴
f(2) = 2 * 16
f(2) = 32
Also
g(x) = 4 x 2ˣ
g(2) = 4 x 2²
g(2) = 4 * 4
g(2) = 16
hence comparing both we can say that
f(2) = 32 is greater than g(2) = 16
Learn more about exponents at
https://brainly.com/question/13669161
#SPJ1
the swim team trains 4 days every week. Mon, Tues, and Thurs, the swim tea spends 1/2h in the gym followed by 1 1/4 in the pool. On Saturday there is no gym work but double the swim team time. how many hours per week does the team train?
Answers
The number of hours that the team trians per week is 17 hours.
How to illustrate the fraction?A fraction simply means a piece of a whole. In this situation, the number is represented as a quotient such that the numerator and denominator are split. In this situation, in a simple fraction, the numerator as well as the denominator are both integers.
Since the the swim tea spends 1/2h in the gym followed by 1 1/4 in the pool. On Saturday there is no gym work but double the swim team time. The number of hours will be:
( 1 1/4 + 1/2 + 2 1/2) × 4
= 4.25 × 4
= 17 hours.
Learn more about fractions on:
brainly.com/question/78672
#SPJ1
What is the smallest number by which 864 must be multiplied with to make the quotient a perfect cube?
Answers
Answer:
Number is two
Step-by-step explanation:
First of all we find the closest factors of 864 which are 32 x 27
Simply them we have
32 x 27 = 2^5 x 3³
So
Next we know that to be aperfect cube, each exponent needs to be equally divided by divisible by 3.
So If we multiply 864 x 2 we get
Then
1728 = 2^6 x 3³
So if we finally
Take the cube root of that is 2²* 3^1 = 4 x 3= 12
So 2² x 3^1
So if we equate the powers we have the answer as 2.
chegg suppose we take a single observqation froma bernouilli population, where the mean is known to be restruction p [1/3, 2/3] what is the maximum likellhiood estimator
Answers
The maximum likelihood estimator (MLE) for a single observation from a Bernoulli population, where the mean is known to be restricted to p [1/3, 2/3], is p = 0.
The maximum likelihood estimator (MLE) for a single observation from a Bernoulli population with a known mean restriction p [1/3, 2/3] can be found by maximizing the likelihood function.
In this case, the likelihood function can be defined as the probability of obtaining the observed value given the parameter p. Since the population follows a Bernoulli distribution, the likelihood function can be expressed as:
\(L(p) = p^x * (1-p)^(1-x)\)
where x is the observed value (0 or 1).
To find the MLE, we need to find the value of p that maximizes the likelihood function. Taking the derivative of the log-likelihood function with respect to p and setting it equal to zero, we can solve for the MLE.
The log-likelihood function for a single observation from a Bernoulli distribution is:
\(log L(p) = x * log(p) + (1-x) * log(1-p)\)
Taking the derivative with respect to p:
\(d/dp (log L(p)) = (x/p) - ((1-x)/(1-p))\)
Setting it equal to zero and solving for p:
\((x/p) - ((1-x)/(1-p)) = 0\)
Simplifying the equation, we get:
\(x(1-p) - (1-x)p = 0\)
Expanding the equation further, we get:
x - px - p + xp = 0
2xp - 2p = x
Factoring out p, we get:
\(p(2x-2) = x\)
Dividing both sides by (2x-2), we get:
p = x / (2x-2)
In this case, since the mean is restricted to the range [1/3, 2/3], we need to consider the possible values of x (0 or 1) and substitute them into the equation to find the MLE.
For x = 0:
p = 0 / (2*0-2)
= 0
For x = 1:
p = 1 / (2*1-2)
= 1 / 0
= undefined
Therefore, the maximum likelihood estimator (MLE) for a single observation from a Bernoulli population, where the mean is known to be restricted to p [1/3, 2/3], is p = 0.
To know more about population visit-
https://brainly.com/question/15889243
#SPJ11
It costs $20 to enter an amusement park and $0.50 to go on each ride. You have $24. How many rides are you able to go on?
Answers
Answer:
8 rides
Step-by-step explanation:
20 + .50x = 24
-20 -20
.50x = 4
/.50 /.50
x = 8
Answer:
8
Step-by-step explanation:
If you have $24 and you buy a $20 ticket to get in, you are left with four dollars.
Since each ride is $0.50 and that is half a dollar, you can multiply four times two. This gives you eight.
Therefore, you can ride 8 rides :)
On a coordinate plane, a solid straight line has a positive slope and goes through (negative 4, 1) and (0, 3). Everything below and to the right of the line is shaded. Which linear inequality is represented by the graph? y ≤ 2x + 4 y ≤ one-halfx + 3 y ≥ One-halfx + 3 y ≥ 2x + 3
Answers
Answer: \(y \leq \frac{1}{2} x+3\)
Step-by-step explanation:
If a function has a positive slope, that means the y value is increasing with respect to x. As you go down the x-axis, the y value will continuously increase.
First you want to plot the two sets of coords that they gave you, or else you wont know what the line looks like. Or, you could visually do it in your head. We're going down -4 on the x-axis and down 1 on the y-axis. Then for our second coords, we are going to 0 on the x-axis, then up 3 on the y-axis.
You could plot this for yourself, but im going to do it in my head for simplicity. We also need to find the slope of this function in order for us to find the y-intercept. The slope is change in y divided by the change in x. Subtract the initial position from the final position.
3 - 1 = 2
0 - (-4) = 4
2/4 = 1/2
The new equation is:
\(y=\frac{1}{2} x+b\\plugin(0,3)\\3=\frac{1}{2} (0)+b\\b=3\)
Everything is shaded below and to the right of the line. They said the line was solid, so that means less than or equal to, \(\leq\)
Answer:
B
Step-by-step explanation:
Given the functions {f} and {g} below, find g(f(-1)) f(x)=-x-4 \quad g(x)=-x^{2}-3 x-1 -5 -3 -1 -2 none of these
Answers
The value of g(f(-1)) is -41.
To find the value of g(f(-1)), we substitute the value of f(-1) in the expression of g(x) and then simplify.
We have:
f(-1)=-(-1)-4
=5
Now, we substitute f(-1)=5 in the expression of g(x) and get:
g(f(-1))=g(5)
=-5^2-3(5)-1
=-25-15-1
=-41.
Hence, the answer is -41.
Hence, g(f(-1)) is -41.
To know more about the expression, visit:
brainly.com/question/14083225
#SPJ11
This ellipse is centered at the origin. Find it’s equation. Verticles: (0,-6) (0,6) Foci: (0,-2) (0,2)
Answers
The equation of the ellipse will be x² / 36 – y² / 32 = 1.
What is an ellipse?An ellipse is a locus of a point that moves in a plane such that the sum of its distances from the two points called foci adds up to a constant. It is taken from the cone by cutting it at an angle.
This ellipse is centered at the origin.
Vertices: (0,-6) (0,6)
Foci: (0,-2) (0,2)
Then the equation of the ellipse will be given as
x² / a² – y² / b² = 1
Let c be the distance between the origin to foci.
Then we have
c = 2
And the value of a will be
a = 6
Then the value of a² will be
a² = 6² = 36
The value of b is the distance from center to one of the Co-vertices. Then the value of b² will be
a² – b² = c²
36 – b² = 2²
b² = 36 – 4
b² = 32
Then the equation of the ellipse will be x² / 36 – y² / 32 = 1.
More about the ellipse link is given below.
https://brainly.com/question/19507943
#SPJ1
Build a deterministic FA M
3
for the following language L
3
=L(M
3
)={x over {a,b,c}∣x has strictly more than 3c symbols and does not end in c} For example, abcca ∈
/
L
3
and bacccc ∈
/
L
3
, but cccca ∈L
3
and acbcaaabcccb ∈L
3
.
Answers
The deterministic finite automaton (DFA) M3 for the language L3, where strings have more than 3 'c' symbols and do not end in 'c', is designed with states q0, q1, q2, q3, and q4. Transitions and loops are created to determine acceptance.
To build a deterministic finite automaton (DFA) for the language L3 = {x ∈ {a, b, c}* | x has strictly more than 3 'c' symbols and does not end in 'c'}, we can design the following DFA M3:1. Start with an initial state q0.
2. Create a loop on q0 for 'a', 'b', and 'c' inputs, leading back to q0.
3. From q0, transition to a state q1 on input 'c'. This represents the first 'c' encountered.
4. From q1, create a loop for 'a' and 'b' inputs, leading back to q1.
5. Transition from q1 to q2 on input 'c'. This represents the second 'c' encountered.
6. Similarly, create a loop on q2 for 'a' and 'b' inputs, leading back to q2.
7. Transition from q2 to q3 on input 'c'. This represents the third 'c' encountered.
8. From q3, create a loop for 'a', 'b', and 'c' inputs, leading back to q3.
9. Create a final accepting state q4 and transition from q3 to q4 on 'a' or 'b' inputs.
In this DFA, any string that ends with 'c' or has less than three 'c' symbols will not reach the accepting state q4, hence not belonging to L3.
Therefore, The deterministic finite automaton (DFA) M3 for the language L3, where strings have more than 3 'c' symbols and do not end in 'c', is designed with states q0, q1, q2, q3, and q4. Transitions and loops are created to determine acceptance.
To learn more about automaton click here
brainly.com/question/33332366
#SPJ11
when studying the relationship between test performance (exam score) and length of sleep (the night before), which type of hypothesis is being examined?
Answers
When studying the relationship between test performance (exam score) and length of sleep (the night before), here the true population correlation is being used.
Correlation:
Correlation analysis examines relationships between variables. The purpose of correlation analysis is to find out whether there are relationships between variables that are unlikely to be caused by sampling error. The null hypothesis states that there is no relationship between the two variables. Correlation analysis provides the following information:
Direction of relationship: positive or negative - indicated by the sign of the correlation coefficient.
Strength or magnitude of relationship between two variables - indicated by the correlation coefficient, which varies from 0 (no relationship between variables) to 1 (perfect relationship between variables).
Positive Correlation:
A positive correlation indicates that high scores for one variable are associated with high scores for the other variable. Low values of one variable are associated with low values of the second variable. For example, in the chart below, a higher score for negative impacts corresponds to a higher score for perceived stress.
Negative Correlation:
A negative correlation indicates that high values of one variable are associated with low values of the other variable. This graph shows that people with higher perceived stress scores are more likely to have lower proficiency scores. The slope of the graph decreases toward the right. In the chart below, the higher the mastery score, the lower the perceived stress score.
Strength or Magnitude of Relationship
The strength of a linear relationship between two variables is measured by a statistic known as the correlation coefficient, which varies between 0 and -1 and 0 and +1. There are some correlation coefficients. The most common are Pearson's r and Spearman's rho. The strength of the relationship is interpreted as follows.
Small/Weak: r= 0.10 to 0.29
Medium/Medium: r= 0.30 to 0.49
Large/Strong: r= 0.50 to 1
Learn more about Population Correlation:
https://brainly.com/question/25822940
#SPJ4
Im struggling a lot with these problems can anyone help and show the WORK please?

Answers
Answer:
Step-by-step explanation:
I'll give a couple answers so you get the gist of things.
All you have to do is substitute 1/2 for x and 3/4 for y.
Ex - 30. x × y = 1/2 × 3/4 = 3/8
Michael needs to memorize words for class. he has memorized 20 which is 4/5 of them. how many does he have left to memorize?
Answers
He have left to memorize = 16 words.
What is percentage?a percentage that represents a tenth of a quantity. One percent, denoted by the symbol 1%, is equal to one hundredth of something; hence, 100 percent denotes the full thing, and 200 percent designates twice the amount specified. percentage.
Percentage derives from the Latin word per centum, which means "by the hundred." The Latin expression was adopted by English in the sixteenth century. In the future, it was shortened to % with a final period. The two sections were eventually combined, the period was omitted, and the result was the contemporary one-word form %.
According to the given information:20 words should be committed to memory.
Has completed 4/5 of the portion.
The number of words he has memorized =
= 20 * 4/5,
which equals 16.
Thus,
The total number of words Ivan has memorized up to this point is sixteen (16), as he has only learnt four of the total (five-fifths), or five sections of four words each. 16 (sixteen) is the answer, therefore.
To know more about percentage visit:
https://brainly.com/question/14883639
#SPJ4
Suppose that 12 inches of wire costs 60 cents.
At the same rate, how many inches of wire can be bought for 25 cents?
Answers
Answer:
5 inches of wire.
Step-by-step explanation:
60/12 = 5
So at .05 an inch, you can afford 5 inches at 25 cents
Please mark brainliest!
how many samples of size n=2 can be drawn from this population
Answers
The samples of size n = 2 that can be drawn from this population is 28
How many samples of size n=2 can be drawn from this populationFrom the question, we have the following parameters that can be used in our computation:
Population, N = 8
Sample, n = 2
The samples of size n = 2 that can be drawn from this population is calculated as
Sample = N!/(n! * (N - n)!)
substitute the known values in the above equation, so, we have the following representation
Sample = 8!/(2! * 6!)
Evaluate
Sample = 28
Hence, the number of samples is 28
Read more about sample size at
https://brainly.com/question/17203075
#SPJ1
Complete question
A finite population consists of 8 elements.
10,10,10,10,10,12,18,40
How many samples of size n = 2 can be drawn this population?
1,2/3,1/4,1/2,1/3 least to greatest
Answers
you throw 3 fair six-sided dice at the same time, what is the expected sum of faces?
Answers
For three fair six-sided dice, the possible sum of the faces rolled can be any digit from 3 to 18.the number of sums will be greater than 16 and the minimum number greater than 16 is 17.
For instance the minimum sum occurs when all three dices shows 1 (i.e. 1 + 1 + 1 = 3) and the maximum sum occurs when all three dces shows 6 (i.e. 6 + 6 + 6 = 18).
Thus, there are 16 possible sums when three six-sided dice are rolled.
Therefore, from the pigeonhole principle, the minimum number of times you must throw three fair six-sided dice to ensure that the same sum is rolled twice is 16 + 1 = 17 times.
The pigeonhole principle states that if n items are put into m containers, with n > m > 0, then at least one container must contain more than one item.
That is for our case, given that there are 16 possible sums when three six-sided dice is rolled, for there to be two same sums, the number of sums will be greater than 16 and the minimum number greater than 16 is 17.
learn more about of sum here
https://brainly.com/question/4176440
#SPJ4
Please help me with this math!!!
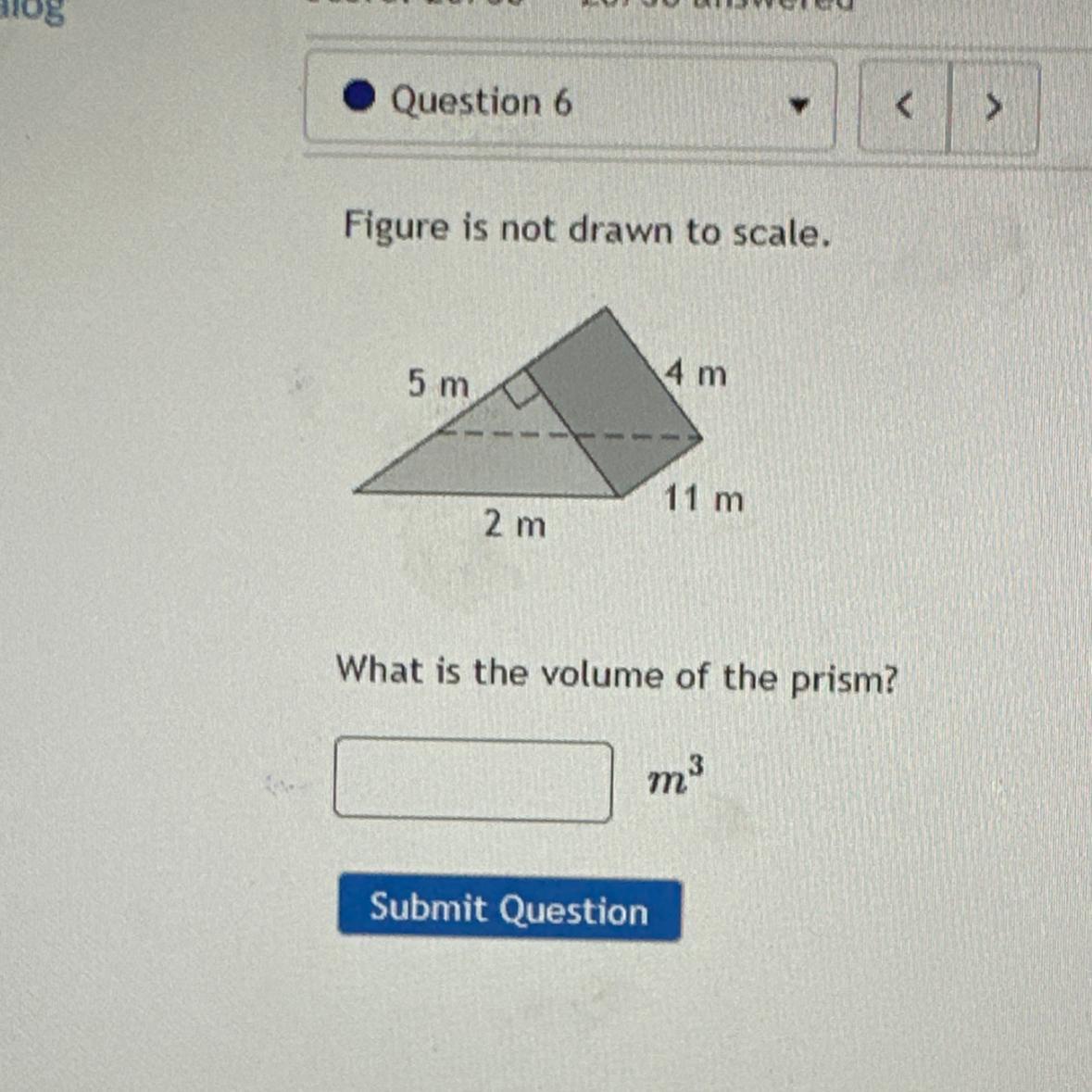
Answers
The volume of the triangular prism is calculated as 176.25m³
What is the volume of a triangular prism?The formula of volume of a triangular prism is given as;
V = 1/4h√(-a⁴ + 2(ab)² + 2(ac)² - b⁴ + 2(bc)² - c⁴
Where;
h = height of the prisma, b, c and d = side lengthsSubstituting the values into the formula above;
V = 1/4* 5√(-2⁴ + 2(2*4)² + 2(2*11)² -4⁴ + 2(4*11)² - 11⁴
V = 176.25m³
The volume of the triangular prism is 176.25m³
Learn more on volume of triangular prism here;
https://brainly.com/question/23491071
#SPJ1
Which is the approximate measure of angle yzx? 34.8° 39.4° 50.6° 55.2°
Answers
The approximate measure of angle YZX is 39.4°. Option(B) is the correct answer.
we know that
In the right triangle XYZ
\(tan(Y Z X)= \frac{opposite side angle YZX}{adjacent side angle YZX}\)
In this problem,
Opposite side angle YZX= XY = 12.4cm
Adjacent side angle YZX= YZ = 15.1cm
substitute the values,
\(tan ( Y Z X) = \frac{12.4}{15.1}\)
\(Angle ( Y Z X) = arc tan( \frac{12.4}{15.1} )\)
Angle ( Y Z X) = 39.4°
So, the approximate measure of angle YZX is 39.4°.
Read more about the right triangle:
https://brainly.com/question/2437195
#SPJ4
The complete question is:
In right triangle XYZ, the right angle is located at vertex Y. The length of line segment XY is 12.4 cm. The length of line segment YZ is 15.1 cm. Which is the approximate measure of angle YZX?
A .34.8°
B .39.4°
C .50.6°
D. 55.2°
We just had the first day of fall, and a sunny 100-day summer has finally ended. Over those 100 days, nclear =62 of them were clear, ncloudy =28 of them were cloudy (but not rainy), and the remaining nrainy =10 were rainy. Denote the probability that a given summer day next year will be clear, cloudy, and rainy by pclear ,pcloudy , and prainy , respectively, and assume that next summer's weather will follow the same pattern as this year's. Please derive expressions for the maximum-likelihood estimates of pclear ,pcloudy , and prainy , in terms of this summer's weather data.
Answers
The maximum-likelihood estimates of the probabilities for clear, cloudy, and rainy summer days next year can be derived from this year's weather data. The estimates are given by the ratios of the number of days with each type of weather to the total number of days in the summer. The maximum-likelihood estimates are pclear = nclear/100, pcloudy = ncloudy/100, and prainy = nrainy/100.
To find the maximum-likelihood estimates of pclear, pcloudy, and prainy, we divide the number of days with each type of weather by the total number of days in the summer. Given that nclear = 62, ncloudy = 28, nrainy = 10, and the total number of days in the summer is 100, we can calculate the estimates as follows:
pclear = nclear/100 = 62/100 = 0.62
pcloudy = ncloudy/100 = 28/100 = 0.28
prainy = nrainy/100 = 10/100 = 0.1
These estimates represent the probabilities of each type of weather occurring on a summer day next year, based on the observed frequencies from this year's data. For example, the estimate of pclear suggests that there is a 0.62 (or 62%) chance of a summer day next year being clear.
It is important to note that these estimates assume that next summer's weather will follow the same pattern as this year's. However, weather patterns can vary, and other factors may influence the probabilities of different weather types. Therefore, these estimates provide a reasonable approximation based on the available data, but they may not accurately reflect the actual probabilities for next year's weather.
Learn more about ratios here:
https://brainly.com/question/13419413
#SPJ11
m=2/3; passes through the point (3,-1)
your response will be the number value for b
Answers
9514 1404 393
Answer:
-3
Step-by-step explanation:
The "b" is the y-intercept in the slope-intercept form ...
y = mx + b
Filling in the given values, we can find b.
-1 = (2/3)(3) +b
-1 = 2 + b . . . . simplify
-3 = b . . . . . . . subtract 2
The value for b is -3.
