Is (-47, -21) a solution to the equation y = x + -26
Yes or No ?
Answers
Answer:
I believe the answer you are looking for is "no"
Related Questions
how to make a calculator in c# windows form application
Answers
To create a calculator in a C# Windows Form application, you can follow these steps:
1. Open Visual Studio and create a new Windows Forms Application project.
2. Design the user interface of the calculator by dragging and dropping the necessary controls from the Toolbox onto the form. You will need buttons for numbers, arithmetic operations (+, -, *, /), and an equals (=) button. You can also add a text box to display the result.
3. Set properties for each control to specify their appearance and functionality. For example, you can set the text property of each button to represent the corresponding number or operation.
4. Write the code for handling button clicks and performing calculations. Double-click on each button to create an event handler for the Click event. Inside the event handler, you can access the button's text property to determine which button was clicked. Use conditional statements and switch-case statements to handle different button clicks.
5. Create variables to store the numbers entered by the user and the result of the calculations. You can use the double data type for these variables.
6. Implement the logic for performing calculations based on the button clicked. For example, when the "+" button is clicked, you can add the two numbers together and display the result in the text box. Similarly, you can handle other arithmetic operations.
7. Use the TryParse method to convert the button's text to a double value and store it in the appropriate variable. This will allow you to perform calculations correctly.
8. Display the result of the calculations in the text box by assigning the calculated value to the text property of the text box.
9. Test your calculator by running the application and clicking on the buttons to perform calculations. Verify that the calculator performs the desired calculations and displays the correct results.
Here is a simplified example of code for handling button clicks and performing calculations in a C# Windows Form application:
```csharp
private double firstNumber;
private double second number;
private string operation;
private void NumberButton_Click(object sender, EventArgs e)
{
Button button = (Button)sender;
textBox.Text += button.Text;
}
private void OperationButton_Click(object sender, EventArgs e)
{
Button button = (Button)sender;
operation = button.Text;
firstNumber = double.Parse(textBox.Text);
textBox.Clear();
}
private void EqualsButton_Click(object sender, EventArgs e)
{
secondNumber = double.Parse(textBox.Text);
double result = 0;
switch (operation)
{
case "+":
result = firstNumber + secondNumber;
break;
case "-":
result = firstNumber - secondNumber;
break;
case "*":
result = firstNumber * secondNumber;
break;
case "/":
result = firstNumber / secondNumber;
break;
}
textBox.Text = result.ToString();
}
```
Remember to adjust the code and customize the user interface according to your specific requirements.
to know more about c# windows here:
brainly.com/question/31252564
#SPJ11
What’s the surface area of this sphere

Answers
Answer:
314
Step-by-step explanation:
A=4πr^2
A= (4)(3.14)(5)^2
A=314
Question :-
What is the surface area of the sphere that has a radius of 5 inches?Answer :-
The surface area of the sphere is 314 inches².\( \rule{180pt}{3pt}\)
Diagram :-
\(\setlength{\unitlength}{1.2cm}\begin{picture}(0,0)\thicklines\qbezier(2.3,0)(2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,2.121)(0,2.3)\qbezier(-2.3,0)(-2.121,-2.121)(0,-2.3)\qbezier(2.3,0)(2.121,-2.121)(-0,-2.3)\qbezier(-2.3,0)(0,-1)(2.3,0)\qbezier(-2.3,0)(0,1)(2.3,0)\thinlines\qbezier (0,0)(0,0)(0.2,0.3)\qbezier (0.3,0.4)(0.3,0.4)(0.5,0.7)\qbezier (0.6,0.8)(0.6,0.8)(0.8,1.1)\qbezier (0.9,1.2)(0.9,1.2)(1.1,1.5)\qbezier (1.2,1.6)(1.2,1.6)(1.38,1.9)\put(0.2,1){\bold{5 \: inches}}\end{picture}\)
Solution :-
As per the provided information in the given question, we have been given that the radius of the sphere is 5 inches. We have been asked to find or calculate the surface area of the sphere.
To calculate the surface area of the sphere, we will use the formula below :-
\(\bigstar \:\:\:\boxed{\sf{\:\:Surface \: Area_{(Sphere)} = 4\pi r^2 \:\:}}\)
Substitute the given values into the above formula and solve for surface area:
\(\sf:\implies Surface \: Area_{(Sphere)} = 4\pi r^2\)
\(\sf:\implies Surface \: Area_{(Sphere)} = (4)(3.14)(5 \: in)^2\)
\(\sf:\implies Surface \: Area_{(Sphere)} = (4)(3.14)(25 \: in^2)\)
\(\sf:\implies Surface \: Area_{(Sphere)} = (4)(78.5 \: in^2)\)
\(\sf:\implies \bold{Surface \: Area_{(Sphere)} = 314 \: inches^2}\)
Therefore :-
The surface area of the sphere is 314 inches².\(\\\)
Learn more about the surface area of the sphere at https://brainly.com/question/28988747
Have a great day! <33
Which functions have the same rate of change?
y=0.3x-6
y=3x-8
y=0.3x+4
y=0.03x+1
1:A and D
2:B and C
3:A and C
4:C and D
Answers
Answer:
Option 3
Step-by-step explanation:
All equations are in slope-intercept form. \(y=mx+b\)
The 'm' is the slope.
The 'b' is the y-intercept.
The slope is also known as the rate of change. So, we would have to look at what replaces 'm' and select two equations that have the same rate of change.
Let's look over the equations:
Equation A:\(y=0.3x-6\)
In this equation, 0.3 replaces 'm', so the rate of change for this equation is 0.3.
Equation B:\(y=3x-8\)
In this equation, 3 replaces 'm', so the rate of change for this equation is 3.
Equation C:\(y=0.3x+4\)In this equation, 0.3 replaces 'm', so the rate of change for this equation is 0.3.
Equation D:\(y=0.03x+1\)In this equation, 0.03 replaces 'm', so the rate of change for this equation is 0.03.
Equation C and equation A have 0.3 as the slope. Since the question asks for two equations that have the same rate of change, the answer would be Equations A and C, or Option 3.
ven the function f(x)=x^(2)+7x+6, determine the average rate of change of e function over the interval -4<=x<=-1
Answers
The average rate of change of the function f(x) = x² + 7x + 6 over the interval -4 ≤ x ≤ -1 is -8/3 or about -2.67.
To determine the average rate of change of a function over a specific interval, we use the following formula:
\($$ \frac{f(b) - f(a)}{b - a} $$\)
where a and b are the endpoints of the interval.
In this case, we have the function f(x) = x² + 7x + 6 and the interval -4 ≤ x ≤ -1. To find the average rate of change of the function over this interval, we need to evaluate the function at the endpoints of the interval and substitute these values into the formula.
Therefore:
\($$ \text{Average rate of change} = \frac{f(-1) - f(-4)}{-1 - (-4)} $$\)
We start by evaluating the function at the endpoints of the interval: \($$ f(-1) = (-1)^2+ 7(-1) + 6 = -2 $$\)
\($$ f(-4) = (-4)^2 + 7(-4) + 6 = 6 $$\)
Substituting these values into the formula, we get: \($$ \text{Average rate of change} = \frac{-2 - 6}{-1 - (-4)} = \frac{-8}{3} $$\)
Therefore, the average rate of change of the function f(x) = x² + 7x + 6 over the interval -4 ≤ x ≤ -1 is -8/3 or about -2.67.
To know more about function, visit:
https://brainly.com/question/30721594
#SPJ11
which expression is equivalent to...........

Answers
Answer:
6.5y-11
Step-by-step explanation:
i think that's the answer. if I'm wrong tell me right away good day

Let f(x) = 4x3 + 3x2 − 20x − 15 and g(x) = 4x + 3. Find f of x over g of x.
x2 − 5
4x2 + x
x2 − 5x
4x2 + 12
Answers
Answer:
not B
Step-by-step explanation:
I took the test
William is thinking of 2 numbers. The larger number is four less than two times the smaller
number. The sum of the numbers is 104. What are William's numbers? Please write your
answer in a sentence.
Answers
Answer:
The numbers are 36 and 68.
Step-by-step explanation:
Let the smaller number be x.
"The larger number is four less than two times the smaller
number."
The larger number is
2x - 4
The sum of the numbers is x + 2x - 4, or 3x - 4.
"The sum of the numbers is 104."
3x - 4 = 104
3x = 108
x = 36
The smaller number is 36.
The larger number is 2x - 4, or
2x - 4 = 2(36) - 4 = 72 - 4 = 68
The larger number is 68.
Answer: The numbers are 36 and 68.
for the velocity distribution u = −by, v = bx, w = 0, evaluate the circulation γ about the rectangular closed curve defined by (x, y) = (1, 1), (3, 1), (3, 2), and (1, 2). interpret your result.
Answers
The circulation γ about the rectangular closed curve defined by (x, y) = (1, 1), (3, 1), (3, 2), and (1, 2) is given by γ = 2b. This result is independent of the shape of the curve C and depends only on the velocity field v. This means that if we change the curve C while keeping the velocity field v fixed, the value of the circulation γ will remain the same.
We can evaluate the circulation γ about the rectangular closed curve defined by (x, y) = (1, 1), (3, 1), (3, 2), and (1, 2) by using Stokes’ Theorem. The circulation γ is given by:γ=∮Cv⋅dlwhere C is the closed curve and dl is an infinitesimal element of the curve.We can use Stokes’ Theorem to evaluate the circulation γ as follows:∮Cv⋅dl=∬S(∇×v)⋅dS,where S is any surface whose boundary is C. In this case, we can choose the surface S to be the rectangular surface defined by the points (1, 1, 0), (3, 1, 0), (3, 2, 0), and (1, 2, 0). Note that this surface lies in the xy-plane, and that its boundary is C. Therefore, we have:∮Cv⋅dl=∬S(∇×v)⋅dS=∬S(0, 0, b)⋅dS=bdS,where dS is an infinitesimal element of area on S. Since S is a rectangle with sides of length 2 and 1, we have:dS=dx dy=2 dy.Integrating over S, we get:γ=b∬S dS=b(2)(1)=2b.
From the above calculations, we can conclude that the circulation γ about the rectangular closed curve defined by (x, y) = (1, 1), (3, 1), (3, 2), and (1, 2) is given by γ = 2b. This result is independent of the shape of the curve C and depends only on the velocity field v. This means that if we change the curve C while keeping the velocity field v fixed, the value of the circulation γ will remain the same.
To know more about closed curve visit:
brainly.com/question/31598617
#SPJ11
At sea level, the weight of the atmosphere exerts a pressure of 14.7 pounds per square inch, commonly referred to as 1 atmosphere of pressure. as an object decends in water pressure P and depth d are Einearly relaind. In hnit water, the preseute at a depth of 33 it is 2 - atms, ot 29.4 pounds per sraase inch. (A) Find a linear model that relates pressure P (an pounds per squsre inch) to depth d (in feed. (B) intergret the sloce of the model (C) Find the pressure at a depth of 80f. (D) Find the depth at which the pressure is 3 atms.
Answers
A) The equation of the linear model that relates pressure P (in pounds per square inch) to depth d (in feet) is: P = 0.45d + 14.7. B) Integral of the slope of the model = P = 0.45d + 14.7. C) The pressure at a depth of 80 feet is 50.7 pounds per square inch. D) The depth at which the pressure is 3 atm is 65.333 feet.
Given information:
At sea level, the weight of the atmosphere exerts a pressure of 14.7 pounds per square inch, commonly referred to as 1 atmosphere of pressure. as an object descends in water pressure P and depth d are Linearly relaind.
In h nit water, the preseute at a depth of 33 it is 2 - atms, ot 29.4 pounds per square inch.
(A) Linear model that relates pressure P (in pounds per square inch) to depth d (in feet):Pressure exerted by a fluid is given by the formula P = ρgh, where P is pressure, ρ is the density of the fluid, g is the acceleration due to gravity, and h is the height of the fluid column above the point at which pressure is being calculated.
As per the given information, At a depth of 33 feet, pressure is 29.4 pounds per square inch.
When the depth is 0 feet, pressure is 14.7 pounds per square inch.
The difference between the depths = 33 - 0 = 33
The difference between the pressures = 29.4 - 14.7 = 14.7
Let us calculate the slope of the model; Slope = (y2 - y1)/(x2 - x1)
Slope = (29.4 - 14.7)/(33 - 0)Slope = 14.7/33
Slope = 0.45
The equation of the linear model that relates pressure P (in pounds per square inch) to depth d (in feet) is:
P = 0.45d + 14.7
(B) Integral of the slope of the model:
Integral of the slope of the model gives the pressure exerted by a fluid on a surface at a certain depth from the surface.
Integral of the slope of the model = P = 0.45d + 14.7
C) Pressure at a depth of 80 feet:
We know, the equation of the linear model is: P = 0.45d + 14.7
By substituting the value of d in the above equation, we get: P = 0.45(80) + 14.7P = 36 + 14.7P = 50.7
Therefore, the pressure at a depth of 80 feet is 50.7 pounds per square inch.
D) Depth at which the pressure is 3 atms:
The pressure at 3 atmospheres of pressure is: P = 3 × 14.7P = 44.1
Let d be the depth at which the pressure is 3 atm. We can use the equation of the linear model and substitute 44.1 for P.P = 0.45d + 14.744.1 = 0.45d + 14.7Now we can solve for d:44.1 - 14.7 = 0.45d29.4 = 0.45dd = 65.333 feet
Therefore, the depth at which the pressure is 3 atm is 65.333 feet.
Learn more about integral here:
https://brainly.com/question/31109342
#SPJ11
In a holiday resort, the ratio of men to women is 5 : 6 and the ratio of women to children is 4 : 7. There are 200 men staying at the resort. How many children are there?
Answers
Answer:
74.7976
Step-by-step explanation:
Evaluate the expression when y=-4. y²+5y +7
Answers
\(▪▪▪▪▪▪▪▪▪▪▪▪▪ {\huge\mathfrak{Answer}}▪▪▪▪▪▪▪▪▪▪▪▪▪▪\)
Value of given expression is :
\(3\)\( \large \boxed{ \mathfrak{Explanation}}\)
Let's Evaluate :
\( {y}^{2} + 5y + 7\)now, let's plug the value of y as -4
\(( - 4) {}^{2} + (5 \times - 4) + 7\)\(16 - 20 + 7\)\(23 - 20\)\(3\)Answer: 3
Step-by-step explanation:
(-4)(-4) +5(-4) +7 = 3
You replace Y with -4 and Solve
Jara wants to select a negative integer that is closer to zero than -3 on the number line. How many possible choices does she have?
Answers
Jara has 2 alternatives: -2 and -1 A number line is a diagram that depicts numbers,
As we walk along the line from left to right, the numbers rise. Positive numbers are often to the right and negative numbers to the left of zero, which is typically in the middle of the line.
Jara wants to choose a negative number that, in this instance, is closer to zero than -3. This suggests that instead of choosing -3, she should choose a negative integer that is situated nearer to zero on the number line.
-2 and -1 are the two negative numbers that are nearer to zero than -3. On the number line, these values are to the right of -3 and are nearer to zero than -3.
To know more about Integer
brainly.com/question/929808
#SPJ4
What is the equation of a line that passes through the points, (-2, 2) and is parallel to a line with an equation of y = 2x + 5
Answers
Answer:
y = 2x+6
Step-by-step explanation:
y = 2x + 5
This line is in slope intercept form y = mx+b where m is the slope and b is the y intercept
The slope is 2. Parallel lines have the same slope
y = 2x+b
Using the given point and substituting it into the equation
2 = 2(-2) +b
2 =-4+b
Add 4 to each side
2+4 = -4+b+4
6 = b
y = 2x+6
If, in a sample of n = 25 selected from a normal population, X = 55 and S-10, how many degrees of freedom does the t-test have if you are testing the null hypothesis H0 : μ-50 ?
Answers
The t-test for testing the null hypothesis H0 : μ = 50 with a sample size of n = 25 has 24 degrees of freedom.
The t-test is a statistical test used to compare the means of two samples or to test hypotheses about a population mean. The number of degrees of freedom for a t-test is defined as n - 1, where n is the sample size.
In this case, the sample size is n = 25, so the degrees of freedom for the t-test is 25 - 1 = 24. The null hypothesis is H0 : μ = 50, which means that the population mean is equal to 50. The sample mean is X = 55, and the sample standard deviation is S = 10.
To perform the t-test, we calculate the t-statistic as (X - μ) / (S / sqrt(n)), where X is the sample mean, μ is the hypothesized population mean under the null hypothesis, S is the sample standard deviation, and n is the sample size. Plugging in the values, we get
t = (55 - 50) / (10 / sqrt(25)) = 2.5.We can then use the t-distribution with 24 degrees of freedom to calculate the p-value associated with the t-statistic. If the p-value is less than the significance level, we reject the null hypothesis.
Learn more about the Null Hypothesis:
https://brainly.com/question/4436370
#SPJ4
Solve this system of equations using any method.
y=5x + 4
y = 6x + 1
Question 6 options:
(3,19)
(5,-4)
(-3,-6)
(3,4)
Answers
The solution to the system of equation y = 5x + 4 and y = 6x + 1 is (3,19).
What is the solution to the system of equation?Given the system of equation in the question;
y = 5x + 4
y = 6x + 1
To solve the system of equation, first plug equation one into equation two and solve for x.
y = 6x + 1
Plug in y = 5x + 4
5x + 4 = 6x + 1
Solve for x
6x - 5x = 4 - 1
x = 3
Now, plug x = 3 into equation one and solve for y.
y = 5x + 4
Plug in x = 3
y = 5( 3 ) + 4
y = 15 + 4
y = 19
Therefore, the value of x is 3 and y is 19.
Option A) (3,19) is the correct answer.
Learn more about simultaneous equation here: brainly.com/question/30319215
#SPJ1
f the last 18 trains to pull into Castroville Station, 12 were full. Considering this data, how many of the next 12 trains would you expect to be full?
Answers
Answer:
8
Step-by-step explanation:
first multiple 12 by 12 then divide by 18 then you'll get 2 times 4 and that's how you get 8.
Please I need help ASAP 40. Points

Answers
Total owed = starting amount x( 1 + interest rate) ^ time
The equation would be total = 550(1.12)^x where x is the number of months.
Replace total with 550x2 = 1100 and solve for x
It will double in 6.11 months. Round to 6 months
Earth has a diameter of 7,926 miles. What is its diameter in kilometers? (1 mile = 1.6 kilometers)
A. 49,553 km
B. 120,586 km
C. 1,392,650 km
D. 12,682 km
Answers
The diameter of Earth in kilometers is approximately 12,682 km, making option D the correct answer.
To convert the diameter of Earth from miles to kilometers, we can multiply the given diameter in miles by the conversion factor of 1.6 kilometers per mile.
Given that Earth's diameter is 7,926 miles, we can calculate its diameter in kilometers as follows:
Diameter in kilometers = Diameter in miles × Conversion factor
Diameter in kilometers = 7,926 miles × 1.6 kilometers/mile
Diameter in kilometers = 12,681.6 kilometers
Rounding this value to the nearest whole number, we get 12,682 kilometers.
Therefore, the correct answer is option D: 12,682 km.
Option A: 49,553 km is not the correct answer. It is not consistent with the given diameter of Earth.
Option B: 120,586 km is also not the correct answer. It is not consistent with the given diameter of Earth.
Option C: 1,392,650 km is significantly larger than the actual diameter of Earth and is not a plausible value.
In conclusion, the diameter of Earth in kilometers is approximately 12,682 km, making option D the correct answer.
For more such questions on diameter visit:
https://brainly.com/question/28162977
#SPJ8
HELPPPPP MEEEEE find m

Answers
Answer:
b=180°-69° (adj angles on a str line)
=111°
Two semicircles are used to make the shaded shape below. One semicircle has a diameter of 12 cm and the other has a diameter of 20 cm.

Answers
Answer:58.272
Step-by-step explanation: This is the answer for maths watch
The perimeter of the shaded shape is 58.29 cm.
Semi-Circles:It is half the circle.Its area is given by A = \(\frac{\pi r^2}{2}\) .Its perimeter is given by, P = πr .How to solve the given question?The shaded shape comprises two semi-circles with a diameter of 12cm and 20cm.So, the perimeter of the shaded shape = (perimeter of 12cm diameter semi-circle) + (perimeter of 20cm diameter semi-circle) + (difference of diameter)\(P = \pi r_1 + \pi r_2 + (d_1 - d_2)\\P = (\pi \ \frac{20}{2} ) + (\pi \ \frac{12}{2} ) +(20 -12)\\P = \pi ( 10 + 6) +8\\P = 16\pi +8\\P = 58.29 \ cm\)
Thus, the perimeter of the shaded shape is 58.29 cm.
Learn more about perimeter here:
https://brainly.com/question/14965059
#SPJ2
At the beginning of spring, Samuel planted a small sunflower in his backyard. The sunflower's height in inches,h,after w weeks, is given by the equation h=3.25w+19. What could the number 3.25 represent in the equation?
Answers
In equation h=3.25w+19, the number 3.25 represents the rate of change in the height of the sunflower per week (w), and the constant term of 19 represents the initial height of the sunflower when it was first planted.
The equation h=3.25w+19 is in slope-intercept form, which means that it can be written as y=mx+b, where y represents the dependent variable (in this case, the height of the sunflower), x represents the independent variable (the number of weeks since the sunflower was planted), m represents the slope of the line, and b represents the y-intercept (the value of y when x=0).
In this equation, the slope is 3.25, which means that for each additional week that passes since the sunflower was planted, its height increases by an average of 3.25 inches. So, the number 3.25 represents the rate of change of the height of the sunflower with respect to time.
This means that for every additional week that passes since the sunflower was planted, the height of the sunflower increases by 3.25 inches on average.
The equation also includes a constant term of 19, which represents the initial height of the sunflower when it was first planted, before any weeks had passed.
To learn more about height please click on below link
https://brainly.com/question/28040390
#SPJ1
What is the solution of the inequality shown
below?
y+7≤-1
Answers
The solution to the inequality is y ≤ -8. This means that any value of y that is less than or equal to -8 will satisfy the original inequality.
To solve the inequality y + 7 ≤ -1, we need to isolate the variable y on one side of the inequality sign.
Starting with the given inequality:
y + 7 ≤ -1
We can begin by subtracting 7 from both sides of the inequality:
y + 7 - 7 ≤ -1 - 7
y ≤ -8
The solution to the inequality is y ≤ -8. This means that any value of y that is less than or equal to -8 will satisfy the original inequality.
In the context of a number line, all values to the left of -8, including -8 itself, will make the inequality true. For example, -10, -9, -8, -8.5, and any other value less than -8 will satisfy the inequality. However, any value greater than -8 will not satisfy the inequality.
For such more question on solution:
https://brainly.com/question/24644930
#SPJ8
The following question may be like this:
What is a solution of the inequality shown below? y+7≤-1
Around to the nearest tenth.
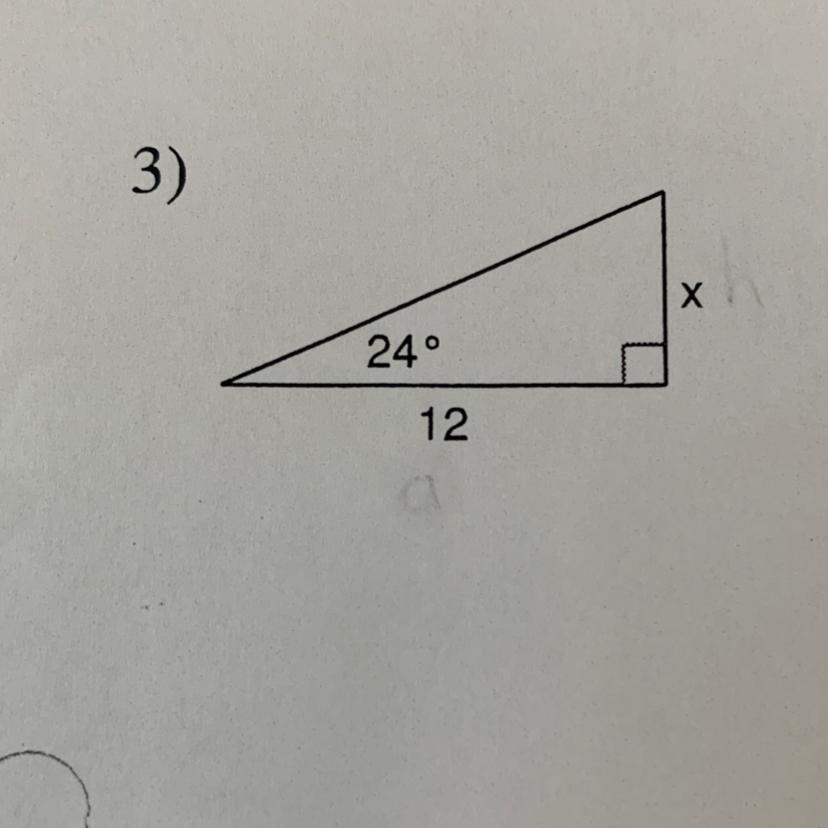
Answers
Answer:
x ≈ 5.3
Step-by-step explanation:
SOH CAH TOA(tangent = opposite side/ adjacent side)
tan (24°) = x/12
=> x = tan (24°) × 12
=> x ≈ 5.3
Numerical Integration • The function f(x)=e* can be used to generate the following table of unequally spaced data = x O 0.1 0.3 0.5 0.7 0.95 1.2 f(x) 1 0.9048 0.7408 0.6065 0.4966 0.3867 0.3012 . =
Answers
Numerical integration is a numerical analysis technique for calculating the approximate numerical value of a definite integral.
In general, integrals can be either indefinite integrals or definite integrals. A definite integral is an integral with limits of integration, while an indefinite integral is an integral without limits of integration.A numerical integration formula is an algorithm that calculates the approximate numerical value of a definite integral. Numerical integration is based on the approximation of the integrand using a numerical quadrature formula.
The numerical quadrature formula is used to approximate the value of the integral by breaking it up into small parts and summing the parts together.Equations for the calculation of integration by trapezoidal rule (1/2)h[f(x0)+2(f(x1)+...+f(xn-1))+f(xn)] where h= Δx [the space between the values], and x0, x1, x2...xn are the coordinates of the abscissas of the nodes. The basic principle is to replace the integral by a simple sum that can be calculated numerically. This is done by partitioning the interval of integration into subintervals, approximating the integrand on each subinterval by an interpolating polynomial, and then evaluating the integral of each polynomial.
Based on the given table of unequally spaced data, we are to calculate the approximate numerical value of the definite integral. To do this, we will use the integration formula as given by the trapezoidal rule which is 1/2 h[f(x0)+2(f(x1)+...+f(xn-1))+f(xn)] where h = Δx [the space between the values], and x0, x1, x2...xn are the coordinates of the abscissas of the nodes. The table can be represented as follows:x 0.1 0.3 0.5 0.7 0.95 1.2f(x) 1 0.9048 0.7408 0.6065 0.4966 0.3867 0.3012Let Δx = 0.1 + 0.2 + 0.2 + 0.25 + 0.25 = 1, and n = 5Substituting into the integration formula, we have; 1/2[1(1)+2(0.9048+0.7408+0.6065+0.4966)+0.3867]1/2[1 + 2.3037+ 1.5136+ 1.1932 + 0.3867]1/2[6.3972]= 3.1986 (to 4 decimal places)
Therefore, the approximate numerical value of the definite integral is 3.1986.
The approximate numerical value of a definite integral can be calculated using numerical integration formulas such as the trapezoidal rule. The trapezoidal rule can be used to calculate the approximate numerical value of a definite integral of an unequally spaced table of data.
To know more about Numerical integration visit
https://brainly.com/question/31148471
#SPJ11
A necklace is bought for $72. Later, it is sold with a profit of %15.
How much is the necklace sold for?
After selling the necklace, how much money has been made?
Answers
Explanation: to find an added percentage of a number, multiply it by 1.[added percentage] or in this case 15. 72(1.15) = 82.8. then for the second question subtract 72 from 82.8 to get a margin of $10.8
You may need to use the appropriate appendix table or technology to answer this question.
A population has a mean of 800 and a standard deviation of 200. Suppose a sample of size 400 is selected and
x
is used to estimate μ. (Round your answers to four decimal places.)
(a)____
What is the probability that the sample mean will be within ±5 of the population mean?
(b)___
What is the probability that the sample mean will be within ±10 of the population mean?
Answers
a. The probability that the sample mean will be within ±5 of the population mean is the area under the normal curve between these two z-scores. b. The lower bound z-score is (-10 - 0) / 10 = -1, and the upper bound z-score is (10 - 0) / 10 = 1. We can use the same normal distribution table or technology to find the probability associated with these z-scores.
(a) To find the probability that the sample mean will be within ±5 of the population mean, we can use the Central Limit Theorem (CLT) and the properties of a normal distribution.
The sample mean, is an unbiased estimator of the population mean, μ. According to the CLT, the distribution of sample means approaches a normal distribution with a mean equal to the population mean and a standard deviation equal to the population standard deviation divided by the square root of the sample size.
= 200 / √400
= 200 / 20
= 10
To find the probability that the sample mean will be within ±5 of the population mean, we can standardize the interval using the z-score:
For the lower bound (-5), the z-score is (-5 - 0) / 10 = -0.5.
For the upper bound (+5), the z-score is (5 - 0) / 10 = 0.5.
We can now use a standard normal distribution table or technology (such as a calculator or statistical software) to find the probability associated with the z-scores -0.5 and 0.5. The probability that the sample mean will be within ±5 of the population mean is the area under the normal curve between these two z-scores.
(b) To find the probability that the sample mean will be within ±10 of the population mean, we follow the same steps as in part (a).
The lower bound z-score is (-10 - 0) / 10 = -1, and the upper bound z-score is (10 - 0) / 10 = 1. We can use the same normal distribution table or technology to find the probability associated with these z-scores.
Note: Since the question mentions rounding answers to four decimal places, please use the appropriate table or technology to obtain the precise probabilities for parts (a) and (b).
Learn more about probability here
https://brainly.com/question/25839839
#SPJ11
The residents of a city voted on whether to raise property taxes. The ratio of yes votes to no votes was 5 to 7. If there were 6489 no votes, what was the total number of votes?
Answers
Total number of votes is 11124.
What do you mean by ratio and proportion?
Ratios and proportions are mainly described using fractions.
Two quantities are compared to form a ratio.
An equality of two ratios is a proportion.
How to write a ratio?
1. Determine if the ratio is part-to-part or part-to-whole.
2. Calculate parts and wholes as needed.
3. Put the value into the ratio.
4. Simplify proportions if necessary. Integer ratios are preferred.
Given,
Ratio of yes votes to no votes = 5:7
Number of yes votes = 5x
Number of no votes = 7x
According to question , number of no votes = 6489
Therefore, 7x = 6489
x = 6489/7 = 927
Total number of votes = 5x + 7x = 12x = 12(927) = 11124
Therefore, total number of votes is 11124.
To learn more about the ratio and proportion from the given link.
https://brainly.com/question/18437927
#SPJ1
Please fine the answer

Answers
Answer: C. 3^5
Step-by-step explanation:
Answer:
c
Step-by-step explanation:
what is -13.72842 rounded to the nearest tenth
Answers
Answer:
-13.7
Step-by-step explanation:
-13.72842
-13.7284
-13.728
-13.73
-13.7
I rounded this way
Answer:
-13.7 is the answer!Find the input for the following function machine when x=10. Show explanation and work

Answers
Answer:
14
Step-by-step explanation:
-2(10)+34
-20+34
34-20
14