is 5.8 greater then fifty eight hundreths
Answers
Answer:
no
Step-by-step explanation:
fifty eight hundreths= 5,800
5.8<5,800
Related Questions
A Father is three times as old as his son. Five years later he will be only 2 ½ times older than his son: Find their present age
Answers
Answer: the present age of son is 15 years, and the present age of father is 45 years.
Step-by-step explanation:
Let the age of son be 'x' and that of his father be 'y'.
So according to the question, the 1st equation that can be formed will be:
y = 3(x) ->(1)
[as father's age is 3 times the age of son]
Now after 5 years:
Age of son = (x+5)
Age of father = (y+5)
So according to the question, the 2nd equation that can be formed will be:
(y+5) = 2.5×(x+5) ->(2)
[as father is now two and half times old as his son]
Substituting the value of equation (1) in (2), we get:
(3x+5) = 2.5×(x+5)
=> 3x + 5 = 2.5x + 12.5
=> 3x - 2.5x = 12.5 - 5
=> 0.5x = 7.5
=> x = 7.5/0.5 = 15
Thus, the present age of son is 15 years.
Note : we can calculate the age of father by putting the value of x in equation (1) or (2):
y = 3(x) = 3 × 15 = 45 (putting x in equation 1)
Thus, the present age of father is 45 years.
A spinner has three equal sections labeled 1, 2, and 3
Which organized list shows the possible outcomes for spinning the spinner twice?
Ο Α
o 1,1; 1,2; 1,3
o 2,1,2,2,2,3
o 3,1; 3,2; 3,3
ОВ
o 1,2; 1,3
o 2,1,2,3
o 3,1,3,2
Ос.
o 1,1; 1,2; 1,3
o 2.2; 2,3
o 3,3
OD
1,1; 1,2; 1,3
Answers
the answer is hi Step-by-step explanation:
Answer:
answer: A
Hope that helps!
Scores of students: 30 35 40 45 50 6
No of students: 8 12 15 6 5 4.
find the median scores
and the modal score
Answers
Answer:
Scores of students:
Mean: 34.3
Mode: no mode
No. of students:
Mean: 8.3
Mode: no mode
Step-by-step explanation:
(for scores of students)
6, 30, 35, 40, 45, 50
Mean: 6 + 30 + 35 + 40 + 45 + 50 = 206/6 = 34.3
Mode: there are no mode in the set of data.
(for No. of students)
4, 5, 6, 8, 12, 15
Mean: 4 + 5 + 6 + 8 + 12 + 15 = 50/6 = 8.3
Mode: no mode
i need help with the problem PLS help
Answers
1) It's best to draw out a picture of a rectangle and label each corner with the coordinates given: Let's say (-5, 2) is point A, (-5, -2 1/3) is point B, (2 1/2, 2) is point C, and (2 1/2, -2 1/3) is point D.
2) That being said, line AB is one side of the rectangle, BC is another, CD is another, and lastly, AD is the fourth side.
3) We can use the distance formula and plug in the coordinates of each line to find how long every side is. Then you just need to solve it.
For example: if I want to find how long side AB is, I would use the point A (-5, 2) and B (2 1/2, 2) and plug them into the distance formula, where (-5, 2) is (x1, x2) and (2 1/2, 2) is (x2, y2) and solve that.
4) Repeat this process with side BC, CD, and AD, and add the results together. This will be your final answer; the perimeter of the rectangle.
Reuben made a shirt using 7/8yards of red fabric and 1/4yards of yellow fabric. How many more yards of red fabric did Reuben use?
Answers
Answer and Step-by-step explanation:
To find out how many more yards of red fabric Reuben used, we need to subtract the amount of yellow fabric from the amount of red fabric. Since the two fractions have different denominators, we need to find a common denominator before subtracting them. The least common multiple of 8 and 4 is 8, so we can rewrite both fractions with a denominator of 8:
7/8 - 1/4 = 7/8 - (1/4) * (2/2) = 7/8 - 2/8 = (7 - 2)/8 = 5/8
So, Reuben used 5/8 yards more red fabric than yellow fabric.
Of 30 students 1/3 play sports. 2/5 play soccer. How many students play soccer
Answers
Hi there!
»»————- ★ ————-««
I believe your answer is:
4 students.
»»————- ★ ————-««
Here’s why:
Out of the 30 students, 1/3 of them play any type of sport.⸻⸻⸻⸻
\(30 * \frac{1}{3} =10\)
⸻⸻⸻⸻
10 out of 30 students play sports. We need to find (2/5) of that for the people that play soccer.⸻⸻⸻⸻
\(10 * (2/5) = 4\)
⸻⸻⸻⸻
Four students play soccer.»»————- ★ ————-««
Hope this helps you. I apologize if it’s incorrect.
The exponential distribution is a probability distribution for a random variable measured as a rate of an event occurring.
True or False
Answers
The statement "The exponential distribution is a probability distribution for a random variable measured as a rate of an event occurring" is False.
The exponential distribution is a probability distribution for a continuous random variable representing the time between independent Poisson events occurring at a constant average rate. It is not a probability distribution for a random variable measured as a rate of an event occurring.
The probability density function of the exponential distribution is given by f(x) = \(\lambda e^(-\lambda x)\), where λ is the rate parameter and x is the time between events. This distribution is commonly used to model the time until the occurrence of the next event in a Poisson process, such as the time between two successive earthquakes or the time between arrivals of customers at a service center.
To learn more about probability refer to:
brainly.com/question/30034780
#SPJ4
for a 5 oz. medium cup of frozen yogurt Phil charges $3.00. toppings cost $0.50 each.
Answers
Write an equation in slope-intercept form for the situation shown in the image
The slope-intercept form of a line is:
y = mx + b
On Phill's Frozen Yogurt Shop, Phill charges $3.00 for a medium cup of frozen yogurt and $0.50 for each topping.
Let's call x=number of toppings selected for the yogurt.
Since each topping costs $0.50, the x toppings cost 0.50x. The total cost (y) is calculated as:
y = 0.50x + 3
For Frank's Pizzeria, the cost (y) of a medium pizza is
y = 10 + 1.75x
Where x is the number of toppings.
To write this equation in slope-intercept form, we only need to rearrange it as follows:
y = 1.75x + 10
Listed below is a table showing the number of employees. 20 years or older by gender in the United states
Answers
The total number of workers that were studied can be found to be 139,340,000.
The percent of workers unemployed would be 5. 4 %.
Percentage of unemployed men is 5. 6 % and unemployed women is 5. 1%.
How to find the employment figures ?Number of employed workers :
= 74,624,000 + 64, 716, 000
= 139,340,000
Percentage unemployed :
= ( 4, 209,000 + 3,314,000 ) / 139,340,000
= 5. 4 %
Percentage of unemployed men :
= 4,209,000 / 74,624,000
= 5.6 %
Percentage of unemployed women:
= 3,314,000 / 64, 716, 000
= 5. 1 %
Find out more on unemployment at https://brainly.com/question/13280244
#SPJ1
The full question is:
a. How many workers were studied?
b. What percent of the workers were unemployed?
c. Compare the percent unemployed for the men and the women.
If the lengths of two adjacent sides of a parallelogram area a and b, and if the acute angle formed by these two sides is theta, show that the product of the lengths of the two diagonals is given by the expression (a^2 + b^2)^2 - 4a^2b^2cos^2theta
Answers
√(a² + b²)² - 4a²b²cos²θ is the product of the lengths of the two diagonals is given by the expression.
What is a mathematical expression?
A mathematical expression is a phrase that includes at least two numbers or variables, at least one arithmetic operation, and the expression itself. This mathematical operation may be addition, subtraction, multiplication, or division.
An expression's structure is as follows: Number/variable, Math Operator, Number/Variable is an expression.
we have AB as a, AD as b and the angle between them is theta.
So using the cosine rule, we have
BD = √a² + b² - 2abcosθ
So now consider the triangle ABC
Here AB is a, BC is b and the angle is 180-theta
So using cosine rule, we get AC as
AC = √a² + b² - 2abcosθ( 180 - θ )
AC = √a² + b² - 2ab(-cosθ )
AC = √a² + b² - 2abcosθ
Now we have the two diagonals AC and BD. So multiplying, we get
AC × BD = √a² + b² + 2abcosθ × √a² + b² - 2abcosθ
Simplifying, we get
AC × BD = √(a² + b² + 2abcosθ) × (√a² + b² - 2abcosθ)
AC × BD = √(a² + b²)² - (2abcosθ)²
AC × BD = √(a² + b²)² - 4a²b²cos²θ
Learn more about the expression
brainly.com/question/29052794
#SPJ4
Convert 12 quarts = how many cups? And fluid ounces?
Answers
Answer:
\(12\text{ quarts= 48 cups = 384 fluid ounces}\)Step-by-step explanation:
Use the conversion for quarts to cups:
\(1\text{ Quarts = 4 Cups}\)And, flor fluid ounces:
\(1\text{ Quarts=}32\text{ fluid ounces}\)Therefore, for 12 quarts;
\(\begin{gathered} 12\cdot4=48\text{ Cups} \\ 12\cdot32=384\text{ fluid ounces} \end{gathered}\)Solve the inequality for x
5 3/2 x 2 1/3
Answers
Answer:
A
Step-by-step explanation:
5 - \(\frac{3}{2}\) x ≥ \(\frac{1}{3}\)
multiply through by 6 ( the LCM of 2 and 3 ) to clear the fractions
30 - 9x ≥ 2 ( subtract 30 from both sides )
- 9x ≥ - 28
divide both sides by - 9 , reversing the symbol as a result of dividing by a negative quantity.
x ≤ \(\frac{28}{9}\)
What is this??? Please help me
Answers
Answer:
(3A - Z) / 4
Step-by-step explanation:
A = (1/3) (4c+z)
3A = 4c + z
3A - z = 4c
c = (3A - z) / 4
A new firehouse is being built equidistant from three other fire stations. Positioned on a grid, the current fire stations would be located at (2,2) , (3, -5) , and (-5,-5). Find the coordinates of the new firehouse.
Answers
Answer:
(-1, -2)
Step-by-step explanation:
The point on the grid that is equidistant from the three given points is the center of a circle through those three points. That center is the point of intersection of the perpendicular bisectors of the sides of the triangle connecting the given points.
__
For points A(2, 2), B(3, -5), and C(-5, -5), we want to find the intersection of the perpendicular bisectors of AB, BC, and AC. It is convenient to choose pairs of points that make the computation easier. Points A and C have identical x- and y-values, so they lie on the line y=x. Points B and C have identical y-values, so lie on the horizontal line y=-5.
ACAs we observed, the line AC has equation y=x, so has a slope of 1. Its perpendicular will have a slope of -1. The midpoint of AC is ...
midpoint AC = (A +C)/2 = ((2, 2) +(-5, -5))/2 = (-3/2, -3/2)
In point-slope form, the equation of the perpendicular bisector of AC is ...
y -k = m(x -h) . . . . . . line with slope m through point (h, k)
y -(-3/2) = -1(x -(-3/2)) . . . . line with slope -1 through (-3/2, -3/2)
y = -x -3 . . . . . . . . . simplify to slope-intercept form
BCThe midpoint of BC is ...
midpoint BC = (B +C)/2 = ((3, -5) +(-5, -5))/2 = (-2, -10)/2 = (-1, -5)
The perpendicular to the horizontal line y = -5 will be a vertical line. It must pass through the midpoint we found, so its equation will be ...
x = -1
new firehouseThe circle center is the solution to the system ...
y = -x -3x = -1That solution will be ...
(x, y) = (-1, -(-1) -3)) = (-1, -2)
The new firehouse coordinates are (-1, -2).
A car is driving away from El Paso with constant velocity. At 1 p.m., it is 145 miles away from El Paso. At 3 p.m., it is 275 miles away from El Paso.
Part A: Write a linear function that describes the distance (in miles) the car is from El Paso in terms of time (in hours after 12:00 p.m.).
Answers
The linear function that describes the distance (in miles) is therefore y = 65x + 80
How to solve for the linear functionWe have to find the slope and the intercept in other to get the linear function
The data points are:
(1, 145) and (3, 275).
m = (y2 - y1) / (x2 - x1)
fixing the data points we have
m = (275 - 145) / (3 - 1)
= 130 / 2
= 65
y = mx + b
(1, 145):
145 = 65(1) + b
b = 145 - 65
= 80
y intercept is 80
The linear function is therefore y = 65x + 80
Read more on linear function herehttps://brainly.com/question/15602982
#SPJ1
Lucy bought a couch that cost $1,000.00. she bought it using her debit card. She forgot she only has $900 in her checking account. What should lucy be worried about? 1) how much tax is included 2) discounts 3) nothing 4) overdraft fees
Answers
Answer:
4) overdraft fees
Step-by-step explanation:
if she now has a negative balance then she owes money to the couch store
Answer:
Overdraft fees
Step-by-step explanation:
An overdraft occurs when money is withdrawn in excess of what is on the current account. In this situation the account is said to be "overdrawn".
A training field is formed by joining a rectangle and two semicircles, as shown below. The rectangle is 86m long and 64m wide. Find the area of the training field. Use the value 3.14 for π, and do not round your answer. Be sure to include the correct unit in your answer.
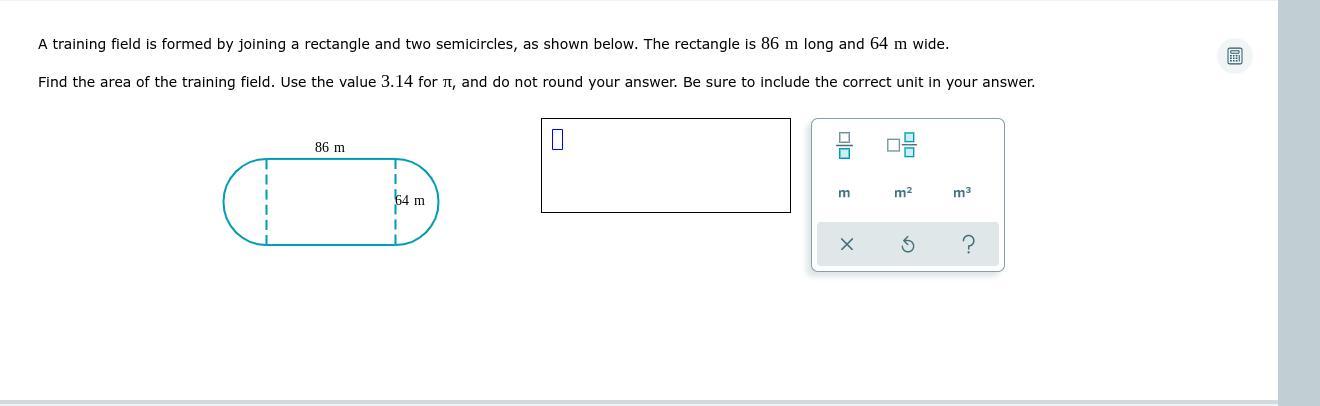
Answers
The area of the training field to the nearest whole number is 8719 msq. meter
Area of composite solidThe given field is made up of a rectangle and 2 semi circles. The formula for calculating the area of the field is:
Area of the field = area of circle + area of rectangle
Area of field = 3.14(32)² + (86)(64)
Area of field = 3215.36 + 5504
Area of the field = 8719 msq. meter
Hence the area of the training field to the nearest whole number is 8719 msq. meter
Learn more on area of composite shapes here: https://brainly.com/question/8370446
#SPJ1
Extend the pattern below by four terms write an observation about the pattern pattern 76, 70, 64,58,52
Answers
Answer:
46, 30, 24, 18, 12
Step-by-step explanation:
What is an equation of the line that passes through the point (6, -2) and is parallel
to the line 5x + 3y = 6?
Answers
Answer:
y= -5/3x + 8
Step-by-step explanation:
parallel lines have the same slope
5x + 3y = 6
3y = -5x + 6
y = -5/3x + 2
the new line will have the slope (-5/3x)
y = (-5/3x) + b
plug in the (x, y) value to find b
-2 = -5/3(6) + b
-2 = -10 + b
b = 8
your equation is: y= -5/3x + 8
Why is it not possible to make a right triangle using lengths of 4 feet, 8 feet, and 10 feet? A. 4 + 8 is greater than 10.B. 10 - 8 does not equal 4.C. 4^2 + 8^2 does not equal 10^2which is the answer?A.B.C.
Answers
If three sides are the sides of a right triangle, then the greatest side is the hypotenuse and the lengths should satisfy the Pyhtagorean Theorem:
\(a^2+b^2=c^2\)Notice that:
\(\begin{gathered} 4^2+8^2=16+64=80 \\ 10^2=100 \end{gathered}\)Since:
\(4^2+8^2\ne10^2\)Then, 4, 8 and 10 cannot be the sides of a right triangle.
Therefore, the answer is:
\(C\)
Dmitri wants to cover the top and sides of this box with glass tiles that are 1 cm square. How many tiles will he need? Dmitri will need [Blank] glass tiles. The dimentions are...26 , 15, 8.
Answers
The number of tiles needed to cover the surface area of the box excluding the bottom is: 1,046 tiles.
What is the Surface Area of a Box?The surface area of a box is the area surrounding all its faces. A box has 6 rectangular faces. Therefore, the total surface area of the box equals the sum of all 6 rectangular faces.
What is the Surface Area of a Box?SA = 2(lw + lh + hw), where:
l = lengthw = widthh = height of the boxThe image attached below shows the box Dmitri wants to cover. Since the bottom of the box would be excluded, therefore:
The surface area to be covered = surface area of the box - area of the bottom rectangular face
The surface area to be covered = 2(lw + lh + hw) - (l)(w)
l = 26
w = 15
h = 8
Substitute
The surface area to be covered = 2(l×w + lh + hw) - (l)(w) = 2·(15·26+8·26+8·15) - (26)(15) =
The surface area to be covered = 1436 - 390 = 1,046 cm
Area of one tile = 1 cm square
Number of tiles needed = 1,046/1
Number of tiles needed = 1,046 tiles.
Learn more about Surface Area of a Box on:
https://brainly.com/question/26161002
#SPJ1
North Dakota has 465 campgrounds over 12 counties while West Virginia has 711 campgrounds. If North Dakota was proportional to West Virginia in the number of campgrounds to counties, how many counties would West Virginia be expected to have? Round to the nearest whole number.
Answers
Number of countries would west Virginia be expected to have is 18 countries
The number of campgrounds that North Dakota has = 465 campgrounds
The number of countries = 12 countries
The number of campgrounds that West Virginia has = 711 campgrounds
Given that the North Dakota was proportional to West Virginia in the number of campgrounds to counties.
The proportion will be
465 / 12 = 711 / x
Divide the terms
38.75 = 711 / x
x = 711 / 38.75
Divide the terms
x = 18.4
x ≈ 18 countries
Hence, number of countries would west Virginia be expected to have is 18 countries
Learn more about proportional here
brainly.com/question/7096655
#SPJ1
What is the 15th term of the following sequence? 0.25, 0.5, 1, 2, 4…
Answers
4,096
Solution:In this case, we have a geometric sequence.In a geometric sequence, we use multiplication/division in order to get to the next term.In this case, we multiply each term by 2.So these are the terms:0.25, 0.5, 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1,024, 2,048, 4,096Hope it helps.
Do comment if you have any query.
If Big Bun won 5 out of 25 matches, what percent did he win?
Answers
Answer:
5/25*100=
1/5*100=100+5=20
8. Given AABC~AEDC
What is the value of x?
C. 30
D. 20
A. 15
B. 12
A
E
60
X
C
D
10
40
B
Answers
Answer:
790
Step-by-step explanation:
7098uuilu4645
The equation y=1/5x+3.5 can be used to find the amount of accumulated snow y in inches x hours after 5 P.M. on a certain day. Graph this equation.
Answers
The coordinates of the y-intercept are (0, 3.5) and the coordinates of the x-intercepts are (-17.5, 0). Using these coordinates, the graph of the equation is shown below.
Graphing linear equationsFrom the question, we are to graph the given linear equation.
To graph the equation,
We will determine the coordinates of the x-intercepts and y-intercepts.
When x = 0
y = 1/5x + 3.5
y = 1/5(0) + 3.5
y = 3.5
(0, 3.5)
When y = 0
y = 1/5x + 3.5
0 = 1/5x + 3.5
Multiply through by 5
0 = x + 17.5
x = -17.5
(-17.5, 0)
Using the coordinates of the x-axis and y-axis, the graph of the equation is shown below.
Learn more on Graphing linear equations here: https://brainly.com/question/11860022
#SPJ1
Translate this sentence into an equation. The product of Mabel's age and 4 is 56. Use the variable m to represent Mabel's age.
Answers
Answer:
4m = 56
Step-by-step explanation:
4 * m = 56
4m = 56
4/4m = 56/4
m = 14
A boxcar contains six complex electronic systems. Two of the six are to be randomly selected for thorough testing and then classified as defective or not defective.
a. If two of the six systems are actually defective, find the probability that at least one of the two systems tested will be defective. Find the probability that both are defective.
b. If four of the six systems are actually defective, find the probabilities indicated in part (a).
Answers
Answer:
Step-by-step explanation:
Number of electronic systems = 6
(a) Number of defected systems = 2
Probability of getting at least one system is defective
1 defective and 1 non defective + 2 defective
= (2 C 1 ) x (4 C 1) + (2 C 2) / (6 C 2)
= 3 / 5
(b) four defective
Probability of getting at least one system is defective
2 defective and 2 non defective + 3 defective and 1 non defective + 4 defective
= (4 C 2 ) x (2 C 2) + (4 C 3 )(2 C 1) + (4 C 4) / (6 C 4)
= 1
Answer:
(a)P(At least one defective)\(=0.6\)
P(Both are defective)\(=0.067\)
(b)P(At least one defective)\(=14/15\)
P(Both are defective)\(=0.4\)
Step-by-step explanation:
We are given that
Total number of complex electronic system, n=6
(a)Defective items=2
Non-defective items=6-2=4
We have to find the probability that at least one of the two systems tested will be defective.
P(At least one defective)=\(\frac{2C_1\times 4C_1}{6C_2}+\frac{2C_2\times 4C_0}{6C_2}\)
Using the formula
\(P(E)=\frac{favorable\;cases}{total\;number\;of\;cases}\)
P(At least one defective)\(=\frac{\frac{2!}{1!1!}\times \frac{4!}{1!3!} }{\frac{6!}{2!4!}}+\frac{\frac{2!}{0!2!}\times \frac{4!}{4!}}{\frac{6!}{2!4!}}\)
Using the formula
\(nC_r=\frac{n!}{r!(n-r)!}\)
P(At least one defective)\(=\frac{2\times \frac{4\times 3!}{3!}}{\frac{6\times 5\times 4!}{2\times 1\times 4!}}+\frac{1}{\frac{6\times 5\times 4!}{2\times 1\times 4!}}\)
P(At least one defective)\(=\frac{2\times 4}{3\times 5}+\frac{1}{3\times 5}\)
P(At least one defective)\(=\frac{8}{15}+\frac{1}{15}=\frac{9}{15}\)
P(At least one defective)\(=\frac{3}{5}=0.6\)
Now, the probability that both are defective
P(Both are defective)=\(\frac{2C_2\times 4C_0}{6C_2}\)
P(Both are defective)=\(\frac{\frac{2!}{0!2!}\times \frac{4!}{4!}}{\frac{6!}{2!4!}}\)
P(Both are defective)\(=\frac{1}{\frac{6\times 5\times 4!}{2\times 1\times 4!}}\)
P(Both are defective)\(=\frac{1}{3\times 5}\)
P(Both are defective)\(=0.067\)
(b)
Defective items=4
Non- defective item=6-4=2
P(At least one defective)=\(\frac{4C_1\times 2C_1}{6C_2}+\frac{4C_2\times 2C_0}{6C_2}\)
P(At least one defective)\(=\frac{\frac{4!}{1!3!}\times \frac{2!}{1!1!} }{\frac{6!}{2!4!}}+\frac{\frac{4!}{2!2!}\times \frac{2!}{2!}}{\frac{6!}{2!4!}}\)
P(At least one defective)\(=\frac{2\times \frac{4\times 3!}{3!}}{\frac{6\times 5\times 4!}{2\times 1\times 4!}}+\frac{\frac{4\times 3\times 2!}{2!\times 2\times 1}}{\frac{6\times 5\times 4!}{2\times 1\times 4!}}\)
P(At least one defective)\(=\frac{2\times 4}{3\times 5}+\frac{2\times 3}{3\times 5}\)
P(At least one defective)\(=\frac{8}{15}+\frac{6}{15}=\frac{8+6}{15}\)
P(At least one defective)\(=\frac{14}{15}\)
P(Both are defective)\(=\frac{4C_2\times 2C_0}{6C_2}\)
P(Both are defective)\(=\frac{\frac{4\times 3\times 2!}{2\times 1\times 2!}\times \frac{2!}{2!}}{\frac{6\times 5\times 4!}{2\times 1\times 4!}}\)
P(Both are defective)\(=\frac{\frac{4\times 3\times 2\times 1}{2\times 1\times 2\times 1}}{3\times 5}\)
P(Both are defective)\(=\frac{6}{15}=0.4\)
P(Both are defective)\(=0.4\)
For the function f(x)=x+4−−−−−√
, the average rate of change to the nearest hundredth over the interval 2 ≤ x ≤ 6 is
Answers
The average rate of change of the function f(x) = √(x+4) over the interval 2 ≤ x ≤ 6 is approximately 0.29 to the nearest hundredth.
To find the average rate of change of the function f(x) = √(x+4) over the interval 2 ≤ x ≤ 6, we need to calculate the change in the function divided by the change in the input variable over that interval.
The change in the function between x = 2 and x = 6 is:
f(6) - f(2) = √(6+4) - √(2+4) = √10 - √6
The change in the input variable between x = 2 and x = 6 is:
6 - 2 = 4
So, the average rate of change of the function over the interval 2 ≤ x ≤ 6 is:
(√10 - √6) / 4
To approximate the answer to the nearest hundredth, we can use a calculator or perform long division to get:
(√10 - √6) / 4 ≈ 0.29
For such more questions on function
https://brainly.com/question/11624077
#SPJ8
Find the value of m/5 + 9, when m=50.
Answers
Answer:
19
Step-by-step explanation:
If m=50, then m/5 = 50/5. That is 10. Then you add 9, equaling 19.
Hope this helps!