Answers
Answer:
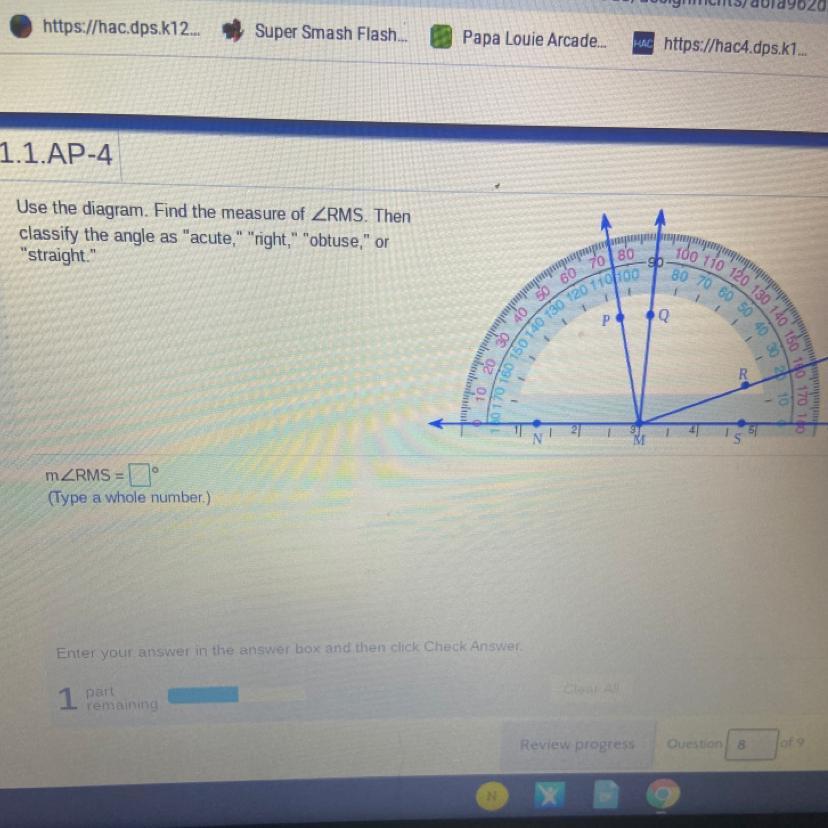
m∠RMS = 20°
Step-by-step explanation:
Find ∠RMS and look at the two values it crosses.
∠RMS crosses through 180 and 160.
Find the difference between the two values to get the measure:
180 - 160 = 20°
So, m∠RMS = 20°
(Its also an acute angle.)
Answer:
20
Step-by-step explanation:
The mistake is in using 160 as the answer. It isn't.
The angle is very small well under 90. It is acute.
The horizontal part of the angle is on 180 degrees of the protractor.
Therefore the angle size is 180 - 160 = 20 degrees.
Related Questions
Perry's school is due west of his house and due south of his friend Sasha's house. The
distance between the school and Sasha's house is 6 miles and the straight-line distance
between Perry's house and Sasha's house is 10 miles. How far is Perry's house from school?
Answers
Answer:
8 miles
Step-by-step explanation:
You can think of it as a triangle, which will look like the picture at the bottom.
You're trying to find the missing length, and to do that you can use the Pythagorean theorem.
That would be:
\(6^{2} + x^{2} =10^{2}\)
Then, solving:
\(36 + x^{2} =100\\x^{2} = 64\\x = 8\)
Therefore, the answer is 8 miles

a student’s height is 145cm. he goes to a pond where the average water depth is 110cm. does this student have a risk in the pond? explain why or why not.
Answers
The student's height is 145cm and the average water depth in the pond is 110cm. Since the student is taller than the average water depth, they would not be at significant risk in the pond, as the water level would likely be below their head. However, it's always important to exercise caution and follow safety guidelines when around water, regardless of depth.
It is difficult to determine if the student is at risk in the pond. Height alone does not necessarily indicate swimming ability or water safety knowledge. However, if the student is not a strong swimmer or lacks knowledge of water safety, they may be at risk in any body of water, including one with an average depth of 110cm. It is important for all individuals to take precautions when swimming, such as wearing a life jacket and staying within their comfort and skill level in the water.
To know more about height visit:
https://brainly.com/question/21836055
#SPJ11
To determine if the student has a risk in the pond based on their height, we need to consider the relationship between the student's height and the water depth.
In this scenario, the student's height is 145 cm, while the average water depth in the pond is 110 cm.
If the water depth is lower than the student's height, it means that the student's head will remain above the water surface, and there is no immediate risk of drowning due to water submersion. In this case, the student's height of 145 cm is greater than the water depth of 110 cm, indicating that the student's head would be above the water, and they would not face an immediate risk in terms of being submerged.
However, it is important to note that other factors could pose a risk in a pond or any body of water, such as the presence of strong currents, slippery surfaces, or the individual's swimming ability. It is crucial to consider these additional factors and exercise caution when in or near bodies of water, regardless of height.
To know more about height visit:
brainly.com/question/29131380
#SPJ11
Which of the following differential equation(s) is/are linear? (Choose all that apply.) 1 2xy" - 5xy' + y = sin(3x) (v)² + xy =In(x) □y' + sin(y)=e3x (x²+1)y"-3y - 2x³y=-x-9 (+1)y'+xy=y"
Answers
To determine which differential equation(s) are linear, we need to examine the form of each equation. A linear differential equation is one that can be written in the form a(x)y" + b(x)y' + c(x)y = g(x), where a(x), b(x), c(x), and g(x) are functions of x.
The differential equation 2xy" - 5xy' + y = sin(3x) is linear. It can be written in the form a(x)y" + b(x)y' + c(x)y = g(x), where a(x) = 2x, b(x) = -5x, c(x) = 1, and g(x) = sin(3x).
The differential equation (v)² + xy = In(x) is not linear. It does not follow the form a(x)y" + b(x)y' + c(x)y = g(x) because it contains a term with (v)², where v represents the derivative of y with respect to x. This term does not have a linear coefficient.
The differential equation y' + sin(y) = e^(3x) is linear. It can be written in the form a(x)y' + b(x)y = g(x), where a(x) = 1, b(x) = sin(y), and g(x) = e^(3x).
The differential equation (x²+1)y" - 3y - 2x³y = -x - 9 is not linear. It does not follow the form a(x)y" + b(x)y' + c(x)y = g(x) because it contains a term with (x²+1)y", where the coefficient is a function of x.
The differential equation y' + xy = y" is linear. It can be written in the form a(x)y' + b(x)y = g(x), where a(x) = 1, b(x) = x, and g(x) = y".
Learn more about differential equation here
https://brainly.com/question/32524608
#SPJ11
Factorise the following expressions
a) 9m^4-9m^3
b) 25x^9y^10-35x^7y^5
c) (x-1)(x-1)-3(x-1)
Answers
Answer:
Step-by-step explanation:
Rules:
Take out the GCF (greatest common factor)
a) \(9m^{4} -9m^{3}\) >take out GCF, what both terms can be divided by
=9m³(m-1) >when taking out GCF, divide both terms by GCF
b) \(25x^{9}y^{10}-35x^{7}y^{5}\) >GCF is \(=5x^{7}y^{5}\)
\(=5x^{7}y^{5}(5x^{2} y^{5}-7)\)
c) (x-1)(x-1)-3(x-1) >GCF is (x-1)
=(x-1) [(x-1) - 3] >within the bracket you can combine like terms
=(x-1) (x-4)
Step-by-step explanation:
A) 9m^4 - 9m^3 = 9m^3 (m - 1)
As for the number, you already took 9 out because it's common for both. As for the m, m^4 is the same as m×m×m×m. So the common between both is m×m×m = m^3.
B) 25x^9y^10 - 35x^7y^5 umm are you sure it's well written? How do you have a power in a power?
C) (x-1)(x-1)-3(x-1) = (x²-1x-1x+1) - (3x-3)
= x² - 2x + 1 - 3x + 3
= x² - 5x + 4
20 POINTS!
Please Help Me!
What is the equation of the line perpendicular to -2x + 3y = -12 and which passes through the point (2, -5)? Write your answer in slope-intercept form. Show all your work.
Answers
Explanation:
the equation of a line in
slope-intercept form
is.
∙
x
y
=
m
x
+
b
where m is the slope and b the y-intercept
rearrange
2
x
−
3
y
=
12
into this form
subtract 2x from both sides
⇒
−
3
y
=
−
2
x
+
12
divide all terms by
−
3
⇒
y
=
2
3
x
−
4
←
in standard form
with
m
=
2
3
given a line with slope m then the slope of a line
perpendicular to it is
∙
x
m
perpendicular
=
−
1
m
⇒
m
perpendicular
=
−
1
2
3
=
−
3
2
⇒
y
=
−
3
2
x
+
b
←
is the partial equation
to find b substitute
(
2
,
6
)
into the partial equation
6
=
−
3
+
b
⇒
b
=
6
+
3
=
9
⇒
y
=
−
3
2
x
+
9
←
equation of perpendicular line
The first three terms of arithmetic progression are -5,-1 and 3.Find the six term.
Answers
Answer:
15
Step-by-step explanation:
The pertinent general formula for this arithmetic progression is
a(n) = a(1) + d(n - 1), where d is the common difference. That difference is d = 4.
Here, a(n) = -5 + 4(n -1)
Therefore, a(6) = -5 + 4(5) = 15
Answer:
It is 15.
Step-by-step explanation:
Alright, first lets find the pattern. Since its a arithmetic sequence, it has something to do with adding/subtracting.
With the values, -5, -1, and 3. Notice something about them? -1 is 4 more than -5 & 3 is 4 more than -1. There's a pattern! The pattern is that for every new term, it is 4 more than the one before it.
With this, we can make a table to find the 6th term!
(Given)
1st Term: -5
2nd Term: -1
3rd Term: 3
Now, continue adding 4 to each term...
4th Term: 7
5th Term: 11
6th Term: 15
For the 6th term, it has been found that the answer's 15.
Find the distance from (-4,3) to (-1,7)
Answers
by using distance formulae

100 POINTS please help!!!!

Answers
Answer:
Standard deviation σ = 1.40 (2 d.p.)
Step-by-step explanation:
If a continuous random variable X is normally distributed with mean μ and variance σ², it is written as:
\(\boxed{X \sim\text{N}(\mu,\sigma^2)}\)
Given:
Mean μ = 13.9 g/dLP(X < 16.2) = 0.95Therefore, if the haemoglobin levels are normally distributed:
\(X \sim\text{N}(13.9,\sigma^2)\)
where X is the haemoglobin level.
Converting to the Z distribution:
\(\boxed{\textsf{If }\: X \sim\textsf{N}(\mu,\sigma^2)\:\textsf{ then }\: \dfrac{X-\mu}{\sigma}=Z, \quad \textsf{where }\: Z \sim \textsf{N}(0,1)}\)
Transform X to Z:
\(\text{P}(X < 16.2)= \text{P}\left(Z < \dfrac{16.2-13.9}{\sigma}\right)= 0.95\)
According to the z-tables, when p = 0.95, z = 1.6449
\(\implies \dfrac{16.2-13.9}{\sigma}=1.6449\)
\(\implies \dfrac{2.3}{\sigma}=1.6449\)
\(\implies \sigma=\dfrac{2.3}{1.6449}\)
\(\implies \sigma=1.40\)
which of the following is true about block design? i. the random assignment of units to treatments in a block design is accomplished in groups. ii. a type of block design is matched pairs. iii. the purpose of blocking is to increase variation in results.
Answers
None of the statements you have provided are true about block design.
Here is an explanation of each statement:
i. The random assignment of units to treatments in a block design is not necessarily accomplished in groups. In a block design, units are randomly assigned to treatments within blocks, where a block is a group of units that are similar in some relevant way. For example, if you are conducting an experiment to compare the effectiveness of different fertilizers on plant growth, you might create blocks based on soil type, since different soil types may have different levels of nutrients that could affect plant growth. Within each block, you would then randomly assign the units (plants) to different fertilizers.
ii. Matched pairs is not a type of block design. Matched pairs is a type of experimental design in which pairs of units are matched on some relevant characteristic (e.g., age, gender, weight, etc.), and one member of each pair is randomly assigned to the experimental treatment while the other is assigned to the control.
iii. The purpose of blocking is not to increase variation in results. The purpose of blocking is to control for variables that could affect the outcome of the experiment. By grouping units that are similar in some way, you can reduce the influence of these variables on the results of the experiment. For example, if you are comparing the effectiveness of different fertilizers on plant growth and you have blocks based on soil type, you can be more confident that any differences in plant growth are due to the fertilizers and not to differences in soil type.
Thus, None of the statements you have provided are true about block design.
To learn more about Block Designing,
visit; brainly.com/question/27231083
#SPJ4
Answer:
Random assignment is done SEPARATELY in the blocks/groups.
Matched pair design IS a type of block design.
The purpose of blocking is to DECREASE variation
DOUBLE CHECK
FLVS has different versions of this exact question. All of the above are true. If your question states that blocking is to increase variation, then that option is NOT true - check EVERYTHING. Otherwise you will not get points.
Step-by-step explanation:
Got this correct on the Segment Exam.
give an example of a sequence of real numbers satisfying each set of properties. (a) cauchy, but not monotone (b) monotone, but not cauchy (c) bounded, but not cauchy
Answers
(a) {(-1)^n/n}, where n is a natural number. The terms alternate in sign but their absolute values converge to 0, making the sequence Cauchy, but not monotone.
(b) {2n}, where n is a natural number. The terms are always increasing but the difference between consecutive terms remains constant (2), so it's not a Cauchy sequence.
(c) {(-1)^n}, where n is a natural number. The terms alternate between -1 and 1, making the sequence bounded, but the difference between consecutive terms is 2, so it's not a Cauchy sequence.
(a) An example of a sequence of real numbers that is Cauchy but not monotone is:
1, 1/2, 2/3, 1/4, 3/5, 1/6, 4/7, 2/8, 5/9, 3/10, 6/11, 4/12, ...
This sequence is Cauchy because, for any two positive integers m and n, the terms a_m and a_n eventually get arbitrarily close to each other as m and n get larger. However, the sequence is not monotone because it oscillates between increasing and decreasing terms.
(b) An example of a sequence of real numbers that is monotone but not Cauchy is:
1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, ...
This sequence is monotone decreasing because each term is smaller than the previous one. However, it is not Cauchy because the difference between any two terms eventually becomes arbitrarily large as the terms get further down the sequence.
(c) An example of a sequence of real numbers that is bounded but not Cauchy is:
1, 1/2, 2/3, 1/4, 4/5, 1/6, 6/7, 1/8, 8/9, 1/10, 10/11, 1/12, ...
This sequence is bounded because all of its terms are between 0 and 1. However, it is not Cauchy because the terms oscillate between small and large values and do not eventually get arbitrarily close to each other.
Learn more about Sequence:
brainly.com/question/30262438
#SPJ11
I only use brainly light mode
Problem: A cylindrical can is to be made to hold 500 cubic centimeters of liquid. Determine the dimensions of the can that minimize the cost of the material to manufacture it, given that the top and bottom are twice as expensive per square centimeter as the sides.

Answers
The dimensions of the can that minimize the cost of the material are approximately:
Radius (r) ≈ 6.324 cm
Height (h) ≈ 3.984 cm
To determine the dimensions of the can that minimize the cost of the material, we need to find the dimensions that minimize the surface area of the can.
Let's assume the can has a height of h and a radius of r.
The volume of a cylinder is given by:
V = πr²h
Given that the can should hold 500 cubic centimeters of liquid, we have:
500 = πr²h
We want to minimize the cost, which depends on the surface area of the can.
The surface area of the can is the sum of the areas of the top, bottom, and side surfaces.
The cost of the top and bottom surfaces is twice as expensive per square centimeter as the sides.
Let's assume the cost per square centimeter of the sides is c, so the cost per square centimeter of the top and bottom surfaces is 2c.
The surface area of the sides of the cylinder is given by:
A_sides = 2πrh
The surface area of the top and bottom surfaces (each) is given by:
A_top_bottom = 2πr²
The total surface area (cost) is given by:
Cost = 2(2c)A_top_bottom + cA_sides
= 4cπr² + 2c(2πrh)
= 4cπr² + 4cπrh
To minimize the cost, we need to minimize the surface area. To do this, we can express the surface area in terms of a single variable, such as the radius (r) or the height (h).
From the volume equation, we have:
h = 500 / (πr²)
Substituting this value of h into the surface area equation, we get:
Cost = 4cπr² + 4cπr(500 / (πr²))
= 4cπr² + 2000c/r
Now, we can take the derivative of the cost function with respect to r, set it equal to zero, and solve for r to find the critical points:
dCost/dr = 8cπr - 2000c/r² = 0
8cπr = 2000c/r²
8πr³ = 2000
r³ = 250 / π
r ≈ 6.324
Now, we can substitute this value of r back into the equation for h:
h = 500 / (π(6.324)²)
≈ 3.984
So, the dimensions of the can that minimize the cost of the material are approximately:
Radius (r) ≈ 6.324 cm
Height (h) ≈ 3.984 cm
Learn more about cylinder click;
https://brainly.com/question/3216899
#SPJ1
True or False? A circle could be circumscribed about the quadrilateral below
A. True
B. False

Answers
The correct answer is option B which is a circle that can not be circumscribed on the given quadrilateral.
What is a circle?The circle is defined as the locus of the point traces around a fixed point called the centre and is equidistant from the outer trace.
In the image we have a quadrilateral having different angles so the vertices of the quadrilateral are also at different positions if we form the circumscribed circle over a given quadrilateral it will not pass through all the vertices of the quadrilateral.
Therefore the correct answer is option B which is a circle that can not be circumscribed on the given quadrilateral.
To know more about circle follow
https://brainly.com/question/24375372
#SPJ1
Help pleaseee :,) thank you !!!!!

Answers
find the angle between two vectors a 5i j and b = 2i-4j
Answers
The angle between two vectors a = 5i + j and b = 2i - 4j is approximately 52.125°.
The angle between two vectors can be calculated using the following formula: cosθ = (a · b) / (||a|| ||b||)
where θ is the angle between the vectors, a · b is the dot product of the vectors, and ||a|| and ||b|| are the magnitudes of the vectors.
In this case, the dot product of the vectors is 13, the magnitudes of the vectors are √29 and √20, and θ is the angle between the vectors. So, we can calculate the angle as follows:
cos θ = (13) / (√29 * √20) = 0.943
The inverse cosine of 0.943 is approximately 52.125°. Therefore, the angle between the two vectors is approximately 52.125°.
Visit here to learn more about vectors:
brainly.com/question/15519257
#SPJ11
What is 7% of 300?
please don’t ignore this lol

Answers
Answer:
7/100×300 you get 21 lol
Answer:
7% of 300 = 21
Step-by-step explanation:
Here's how it's done:
7 ÷ 100 × 300 = 21
Hope this helps! :)
how do you do 4/5 - 2/3 show a picture ANSWER THIS QUICKLY!!!!!!!!!!
please answer this!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Answers
Therefore , the solution of the given problem of fraction comes out to be 4/5 - 2/3 equals 2/15.
What is a fraction?Any arrangement of portions or pieces of similar sizes can symbolize a whole. Standard English refers to quantity as "a fraction" in a specified measure. 8, 3/4. Wholes also include fractions. The ratio of the divisor compared to the ratio is used in mathematics to represent numbers. These are all illustrations of fundamental fractions that split by whole numbers.
Here,
You must identify a common denominator for the two fractions in order to subtract fractions with distinct denominators.
Finding the least common multiple (LCM), which is 15 for the denominators 5 and 3, is one approach to accomplishing this.
After that, you can change both numbers so that their numerator is 15:
=> 4/5 = (4/5) x (3/3) = 12/15
=> 2/3 = (2/3) x (5/5) = 10/15
Since both fractions now have the same denominator, you can simplify the sum by removing their numerators:
=> 12/15 - 10/15 = 2/15
Because of this, 4/5 - 2/3 equals 2/15.
To know more about fraction visit:
https://brainly.com/question/10354322
#SPJ1
Find the exponential form of 27^3*9^2*3
Answers
Answer:
3¹⁴------------------------
We know that:
27 = 3³ and9 = 3²Substitute and evaluate the given expression:
27³ × 9² × 3 = (3³)³ × (3²)² × 3 = 3⁹ × 3⁴ × 3 = 3⁹⁺⁴⁺¹ =3¹⁴Here are the score that Jenna has received on her seven quizzes 16 11 20 16 12 17 18 what is the lower quadrille
Answers
Answer:
12
Step-by-step explanation:
lower quartile is the median of 11, 12, and 16
median: 16
lower q: 12
.........................
Answers
Answer:
according to ur question..
ANSWER IS
.........................
................
...
XD.
Step-by-step explanation:
drop a thanks Pls and follow me
I'm new here....
What is your question?
The midpoint of segment AB is (6,5). The coordinates of point A are (7.10). Find the coordinates of point B.
A)
(8,0)
B)
(5,0)
9
(8, 15)
D)
(-3,7)
PLEASE ANSWER I NEED IT BY TONIGHT kk that’s all
Answers
Answer:
Step-by-step explanation:
(x+7)/2=6
x + 7 = 12
x = 5
(y + 10)/2 = 5
y + 10 = 10
y = 0
(5, 0)
answer is B
Answer:
whatever they said :D
Step-by-step explanation:
Domain:
I need the domain
Answers
Answer:
Domain:The set of possible input values (using the “x” variable), which produce an output from a function.
Step-by-step explanation:
have a great day :)
what is important to remember when converting a music file from analog data to digital data? select two answers what is important to remember when converting a music file from analog data to digital data? continuous values. the samples are compressed to create a smaller digital file. copies of analog data files are more precise. a higher sampling rate will result in a more accurate digital version.
Answers
Note that it is important to remember when converting a music file from analog data to digital data to use:
continuous values and a higher sampling rate will result in a more accurate digital version.What is a higher sampling rate ?
The greater the sample rate, the more snapshots of the audio stream are captured. The audio sample rate, measured in kilohertz (kHz), defines the frequency range sampled in digital audio. under most DAWs, you may change the sample rate under the audio options.
Continuous variables are numerical variables with an endless number of possible values between any two values. A continuous variable can be either numeric or date/time based.
Learn more about higher sampling rate:
https://brainly.com/question/31390480
#SPJ1
Samira babysits for 4.5 hours and earns $22.50. How much does she earn per hour?
P
Answers
Answer:
Samira earns $5 dollars per hour.
Step-by-step explanation:
$22.50 divided by 4.5 hours = $5 dollars
YOO PLZ HELP ASAP!!! MARKING BRAINIEST!!! Use the Internet to find the actual area of Ohio. Then find the actual population density of Ohio. How does this compare with your estimate? Why was your initial estimate greater or less than the actual population density?
Answers
Answer:
The actual area is 44,825 mi², and the actual population density of Ohio is 282.3 people per square mile. I can't answer the estimate part because I don't know what your estimate was. But you can say my estimate was greater than the actual number or less than the actual number. And you can say your estimate was greater/less than the actual population density because I didn't know so many people were in each square mile because a square mile isn't that large.
Step-by-step explanation:
Can't really explain this type of question. :v
Use the following table to answer the question. Standard population for region X:19,000 Standard population for region Y: 8,000 What is the proportionate mortality for young people in region X ? a. 69/115=60% b. 69/117=59% c. 69/184=37% d. 115/184= 63%
Answers
The closest option to this value is option (c) 69/184 = 37%.
To calculate the proportionate mortality for young people in Region X, we need to compare the number of deaths in the young age group to the standard population of Region X.
The proportionate mortality can be calculated using the formula:
Proportionate Mortality = (Number of Deaths / Standard Population) 100
In this case, for the young age group in Region X, the number of deaths is 69, and the standard population is 19,000.
Proportionate Mortality = (69 / 19,000) 100 = 0.363 100 = 36.3%
Therefore, the proportionate mortality for young people in Region X is approximately 36.3%.
The closest option to this value is option (c) 69/184 = 37%.
To calculate proportionate mortality, we would need the number of deaths among young people in region X and divide it by the standard population for region X. The answer would be in the form of a ratio or percentage.
Learn more about Population Calculation here:
https://brainly.in/question/32179158
#SPJ11
In hours 3 3/8, John reads 4 1/2 chapters.
What is the unit rate in chapters per hour?
Write your answer as a fraction or a mixed number in simplest form.
Answers
Answer:
1 1/3 chapters per hour
Step-by-step explanation:
eplaination is in the picture

Indicate whether each situation involves a combination or permutation. Then solve.How many different three-student study groups can be formed from a class of 15 ?
Answers
There are 455 different three-student study groups that can be formed from a class of 15.
This situation involves determining the number of different three-student study groups that can be formed from a class of 15.
To determine whether this situation involves a combination or permutation, we need to consider if the order of selection matters or not, and if repetitions are allowed.
In this case, we are only concerned with forming study groups, and the order of selection does not matter. Additionally, it is assumed that each student can only be selected once for a study group.
Therefore, this situation involves a combination, specifically a combination of 15 students taken 3 at a time.
The formula to calculate the number of combinations is given by:
\(C(n, r) = n! / (r! * (n - r)!),\)
where n is the total number of items to choose from (in this case, the number of students in the class), and r is the number of items being chosen (in this case, the number of students in each study group).
Substituting the values into the formula:
C(15, 3) = 15! / (3! * (15 - 3)!) = 15! / (3! * 12!) = (15 * 14 * 13) / (3 * 2 * 1) = 455.
Therefore, there are 455 different three-student study groups that can be formed from a class of 15.
In summary, this situation involves a combination, and the number of different three-student study groups that can be formed from a class of 15 is 455.
Learn more about groups here
https://brainly.com/question/29047283
#SPJ11
1. What is AC?
AC = 6
AC = 24
AC = 8
AC = 16

Answers
Answer:
AC = 24
Step-by-step explanation:
If you subtract C - A, you get
16 - (-8) = 16 + 8 = 24
Answer:
AC=24
Step-by-step explanation:
OMG HELP NOW PLZZ <3

Answers
Answer:
I think it would be Maxine's, since they did more tests.
A stereo manufacturer determines that in order to sell X units of a new stereo, the price per unit must be p 1000 x. The manufacturer also determines that the cost of producing x units is given by C(x) 3000 + 2Ox. How many units must the company produce and sell in order to maximize the profit? a)490 b)500 c)150 d) 200
Answers
The company must produce 500 units to maximize profit.
A stereo manufacturer determines that in order to sell X units of a new stereo, the price per unit must be p 1000 x.
The manufacturer also determines that the cost of producing x units is given by C(x) 3000 + 2Ox.
We are to determine the number of units that the company must produce and sell in order to maximize the profit.
The revenue obtained from the sale of x units of the new stereo is given byRx = p * x
Where p = 1000x.Rx = 1000x * xRx = 1000x²
The total cost of producing x units of the new stereo is given byC(x) = 3000 + 20x
Therefore, the profit P(x) that is made from the sale of x units of the new stereo is given by:
P(x) = Rx − C(x)P(x)
= 1000x² − (3000 + 20x)P(x)
= 1000x² − 3000 − 20x
The profit function is given by:P(x) = 1000x² − 3000 − 20x
We will differentiate the profit function, then equate it to zero in order to determine the critical points for the maximum profit
P'(x) = 2000x − 20P'(x) = 20(100x − 1)
Critical points occur whenP'(x) = 0
Therefore100x − 1 = 0⇒ 100x = 1⇒ x = 1/100
Thus, the maximum profit is achieved when the company sells 100/1,000= 1/10 units or 10 units.
Hence, the company must produce and sell 500 units to maximize profit. Therefore, option (b) 500 is the correct option.
#SPJ11
Let us know more about profit function : https://brainly.com/question/32582012.