Jack wants to find the height of an olive tree for a science project. Jack is 2 meters tall. He stands 6 meters away from the tree, and his shadow is 4 meters long.
Answers
The height of an olive tree is 5 meters.
Let the height of olive tree be x. The fraction of height of shadow and height of Jack will be equal to the fraction of total distance between tree and shadow end and height of tree. Representing this in equation form -
4/2= (6+4)/x
Performing addition on Right and Side of the equation
4/2 = 10/x
Rewriting the equation according to x
x = (10×2)/4
Performing multiplication on Right and Side of the equation
x = 20/4
Performing division on Right and Side of the equation
x = 5
Thus, the height of tree is 5 meters.
Learn more about height calculation -
https://brainly.com/question/28122539
#SPJ4
Related Questions
proportionality means the slope of a constraint is proportional to the slope of the objective function. T/F
Answers
False. Proportionality between the slopes of a constraint and the objective function is not a general property in optimization. The relationship between these slopes depends on the specific problem and can vary.
The proportionality between the slopes of a constraint and the objective function is not a universal principle in optimization. It is true that in some cases, there may be a proportional relationship between these slopes. This means that if the slope of a constraint increases or decreases, the slope of the objective function will also increase or decrease by a proportional amount. However, it is important to note that this proportionality is not a fundamental characteristic of all optimization problems.
In many optimization problems, the slopes of constraints and the objective function may have different behaviors and may not be directly related. The slopes can vary independently based on the specific problem structure, constraints, and objective function. In some cases, the slopes may even have an inverse relationship, meaning that an increase in the slope of a constraint leads to a decrease in the slope of the objective function, or vice versa.
In conclusion, while proportionality between the slopes of a constraint and the objective function can occur in some optimization problems, it is not a general property and does not hold true for all scenarios. The relationship between these slopes is problem-dependent and can vary significantly.
Learn more about independently : brainly.com/question/31707382
#SPJ11
help and show work pls

Answers
Answer:
80
Step-by-step explanation:
How much cents are in 12 quarterS answer fast!!!!
Answers
Answer: 300 cents or 3 dollars
Step-by-step explanation: 12x25=300.
Answer:
300 CENTS
Step-by-step explanation:
hope this helps
the sscp exam consists of ____ multiple-choice questions, and must be completed within three hours.
Answers
Answer:
125 questions
Answer:
125 questions
Step-by-step explanation:
Type the correct answer in the box. Use numerals instead of words. What value of x makes this equation true? -2x + 3 = -15 x =
Answers
Answer:
x=9
Step-by-step explanation:
plug in the number 9
-2(9)= -18
-18+3= -15
Need Help
A customer made a purchase that totals $54.73. In the same, transaction, the customer was issued a $22.89 refund for a previous purchase. How much did the customer pay?
Answers
\(\sqrt -72 *2\\\)
Answers
Answer:
12i because we have the square root of -144, so we have 144 times -1, and we square root 144 to get 12, and the square root of -1 is i, so we have 12i.
Brainliest please?
I need help with this ( but I need to send another picture that has the answers )
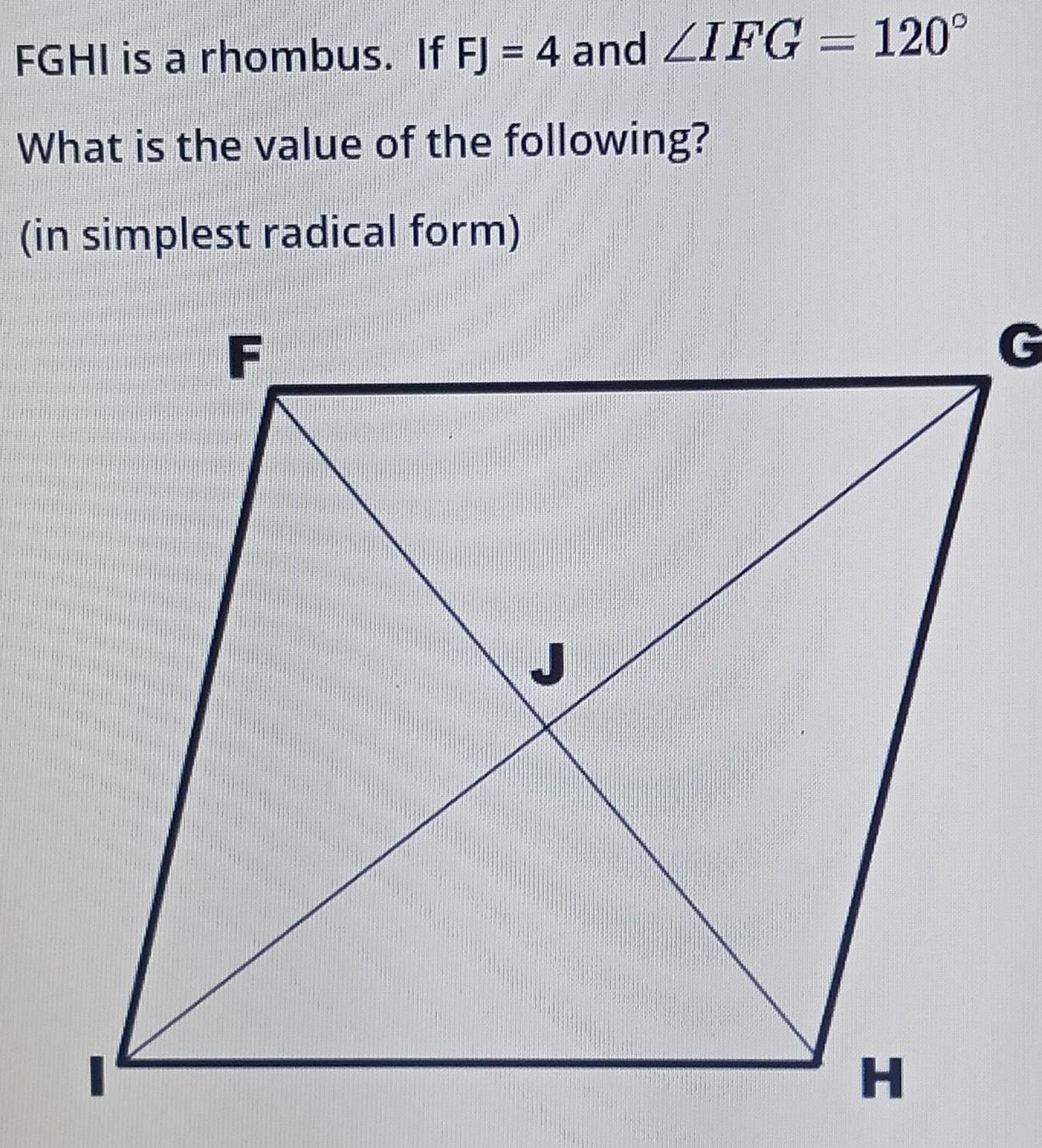

Answers
Step 1:
Draw the figure
The diagonals of a rhombus bisect each other,
therefore
FJ = JH
this implies that
JH = 4.
Opposite angles of a rhombus are equal, so
The diagonals of a rhombus bisect the interior angles.
Therefore,
\(\text{ angle JHG = }\frac{120^0}{2}=60^0\)The diagonals of a rhombus are perpendicular
\(\begin{gathered} Hence, \\ \cos 60^0=\frac{4}{GH} \\ \Rightarrow GH=\frac{4}{\cos60^0}=\frac{4}{\frac{1}{2}}=4\times2=8 \end{gathered}\)GH = 8 (b)
Also,
Using the Pythagorean rule,
\(\begin{gathered} JG^2+4^2=GH^2 \\ \Rightarrow JG^2+16=8^2 \\ \Rightarrow JG=\sqrt[]{64-16}=\sqrt[]{48}=4\sqrt[]{3}=6.928\text{ } \\ \text{right choice is C} \end{gathered}\)FH = FJ + JH
this implies that
FH = 4 + 4 = 8
FH = 8
right choice B
The diagonals of a rhombus bisect the interior angles.
therefore
\(\begin{gathered} angle\text{ JFG = }\frac{angle\text{ IFG}}{2}=\frac{120^0}{2}=60^0 \\ \text{ right choice is h} \end{gathered}\)Sum of the interior angles of a rhombus is 360degrees.
And opposite interior angles of a polygon are congruent.
Therefore
\(2(\text{angle FGH) +2(angle IFG) = 360degr}ees\)\(\begin{gathered} \text{this implies that} \\ 2(\text{angle FGH) = 360 - 2(angle IFG)} \\ \Rightarrow\text{angle FGH = 180 -angle IFG = 180 - 120= }60^0 \\ \text{ right choice is h} \end{gathered}\)\(\begin{gathered} \text{ but }FGJ\text{ = }\frac{FGH}{2}\text{ (diagonals bisect interior angles)} \\ \Rightarrow\text{FGJ =}\frac{60^0}{2}=30^0 \\ \text{right choice is j} \end{gathered}\)Also,
\(\begin{gathered} \(\begin{gathered} \text{JGH}=\text{ }\frac{FGH}{2}=\frac{60}{2}=30^0 \\ right\text{ choice is j} \end{gathered}\)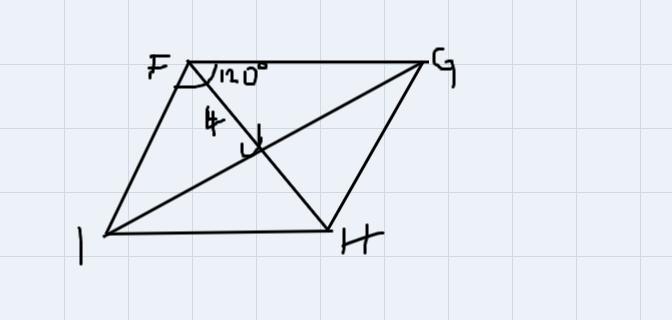
So one pls help plzzzz

Answers
I need help someone please

Answers
Answer:
12 im pretty sure median is like middle
I hope this helps! :)
Answer:
mayve 12
Im sorry if its wrong i took this lesson 3 years ago but i think this is right
A basketball team made $3,094 selling team hats. Each hat sold for $34. How many hats did the team sell?
Answers
Answer:
The team sold 91 hats.
Step-by-step explanation:
$3,094 ÷ %34 = 91
Why?
3,094 divided by 34.
Patel squeezed oranges so that his family could have fresh-squeezed juice for breakfast. He squeezed StartFraction 4 over 17 EndFraction cups from the first orange, StartFraction 3 over 10 EndFraction cups from the second orange, StartFraction 9 over 20 EndFraction cups from the third orange, StartFraction 3 over 11 EndFraction cups from the fourth orange, and StartFraction 7 over 15 EndFraction cups from the fifth orange. Patel estimates that he needs 2 cups of orange juice for his family. About how much more orange juice does he need to reach his estimate?
Answers
Answer:
\(\approx \frac{11}{40}\)
Step-by-step explanation:
Juice squeezed from first orange = \(\frac{4}{17}\) = 0.235
Juice squeezed from second orange = \(\frac{3}{10}\) = 0.3
Juice squeezed from third orange = \(\frac{9}{20}\) = 0.45
Juice squeezed from fourth orange = \(\frac{3}{11}\) = 0.27
Juice squeezed from fifth orange = \(\frac{7}{15}\) = 0.47
Total juice squeezed from all the five oranges = 0.235 + 0.3 + 0.45 + 0.27 + 0.47 = 1.725
Total juice to be squeezed = 2 cups
More juice required = 2 - 1.725 = 0.275 \(\approx \frac{11}{40}\)
Therefore, to make it 2 cups of orange juice for the family, about \(\approx \frac{11}{40}\) cups of more juice is required.
Answer:
1 5/6
Step-by-step explanation: this is what i got from doing the math. please correct me if I'm wrong
In what quadrant does the angle 11pi/4 terminate?
Answers
Answer:
second quadrant
The angle is in the second quadrant.
Step-by-step explanation:
Trust
at the center of a baseball is a sphere called the pill that has an approximate volume of 1.32 cubic inches. the pill is wrapped with 3 types of string to form the center of the baseball. the center of the baseball is covered with a leather casing and sewn together to make the final product. if the radius of the center of the baseball is 2.9 inches, what is the approximate volume of string, to the nearest cubic inch, that is used to wrap the pill?
Answers
The approximate volume of string used to wrap the pill is 1.12 cubic inches.
To calculate the volume of the string used to wrap the pill, we need to find the difference between the volume of the center of the baseball (pill) and the volume of the sphere with the given radius.
The volume of a sphere is given by the formula: V = (4/3)πr^3, where V is the volume and r is the radius.
Given that the volume of the pill is approximately 1.32 cubic inches, we can set up the equation:
1.32 = (4/3)π(2.9^3) + V_string
Solving for V_string, the volume of the string used to wrap the pill, we have:
V_string = 1.32 - (4/3)π(2.9^3)
≈ 1.32 - (4/3)π(24.389)
≈ 1.32 - 121.196
≈ -119.876
Rounding to the nearest cubic inch, we get V_string ≈ -120 cubic inches.
The approximate volume of string used to wrap the pill is 1.12 cubic inches. It's important to note that a negative value was obtained in the calculation, which suggests an error in the calculation or an inconsistency in the given information. Please double-check the provided values to ensure accuracy.
To know more about volume , visit
https://brainly.com/question/27710307
#SPJ11
Solve using the quadratic formula. Select the correct solution.
-7x=2x^2+9

Answers
The answer to your question is B!
Have a wonderful day.

.Kwan is driving at a constant speed. After 141 hours he has driven a total distance of 90 miles. (a) How far will Kwan drive in 2 hours at this rate? (b) If D represents the distance Kwan has driven in miles and t represents the time he has been driving, in hours, then write an equation for D in terms of t. (c) Use your equation from (b) to determine how far Kwan drives in 15 minutes. (d) Kwan is driving a total of 234 miles. How long will his trip take him, to the nearest tenth of an hour, assuming he travels at this constant rate? Use proper units.
Answers
(a) Kwan will drive approximately 1.276 miles in 2 hours at his constant speed. (b) The equation representing the distance Kwan has driven (D) in terms of time (t) is D = 0.638t. (c) Kwan will drive approximately 0.1595 miles in 15 minutes, and (d) Kwan's trip of 234 miles will take approximately 366.8 hours at his constant rate.
(a) To determine how far Kwan will drive in 2 hours at the same constant speed, we can use the concept of proportionality. We can set up a ratio between the distance and time:
Distance / Time = Constant Speed
Let's calculate the constant speed first:
Constant Speed = Distance / Time
= 90 miles / 141 hours
≈ 0.638 miles per hour
Now we can use the constant speed to find the distance Kwan will drive in 2 hours:
Distance = Constant Speed × Time
= 0.638 miles per hour × 2 hours
≈ 1.276 miles
Therefore, Kwan will drive approximately 1.276 miles in 2 hours at this rate.
(b) The equation for D (distance) in terms of t (time) can be written as follows:
D = Constant Speed × t
Using the constant speed calculated earlier (0.638 miles per hour), the equation becomes:
D = 0.638t
(c) To determine how far Kwan drives in 15 minutes (0.25 hours), we can substitute t = 0.25 into the equation from part (b):
D = 0.638 × 0.25
= 0.1595 miles
Therefore, Kwan will drive approximately 0.1595 miles in 15 minutes at this rate.
(d) If Kwan is driving a total of 234 miles, we can rearrange the equation from part (b) to solve for t:
D = 0.638t
234 = 0.638t
Dividing both sides of the equation by 0.638:
t = 234 / 0.638
≈ 366.77 hours
Kwan's trip will take approximately 366.8 hours.
To know more about constant speed refer here:
https://brainly.com/question/26322996#
#SPJ11
Determine whether the statement is true or false.
If f '(x) exists and is nonzero for all x, then f(8) ≠ f(0).
Answers
The statement "If a function f '(x) exists and is nonzero for all x, then f(8) ≠ f(0)" is not necessarily true.
If f(x) is an increasing or decreasing function on the Interval [0, 8], then it is possible that f(8) = f(0).
For example, consider the function f(x) = x, which is increasing on the interval [0, 8] and satisfies f '(x) = 1 for all x in [0, 8]. Then f(8) = 8 and f(0) = 0, so f(8) = f(0).
However, if we assume that f(x) is strictly increasing or strictly decreasing on the interval [0, 8], then the statement would be true.
This is because if f(x) is strictly increasing or decreasing, then it cannot have any repeated values in its range, and so f(8) ≠ f(0).
To Learn More About function
https://brainly.com/question/11624077
#SPJ11
here's this idk its math ig

Answers
Answer:
this is why you pay attention in school kids.
Step-by-step explanation:
any ways i never learned how to do long division but the answer is a decimal
3x^2+ 4x + 5 for x = -2
Answers
3(-2)^2+4(-2)+5
-6^2+ (-8) + 5
36 + (-8) + 5
28+5
33
Please help asap!!!
Will give brainliest

Answers
Answer:
33/2 or
Step-by-step explanation:
2x−7
4
=
x+3
3
(2x−7)*(3)=(x+3)*(4)
6x−21=4x+12
Step 2: Subtract 4x from both sides.
6x−21−4x=4x+12−4x
2x−21=12
Step 3: Add 21 to both sides.
2x−21+21=12+21
2x=33
Step 4: Divide both sides by 2.
2x/2
=
33/2
x=
33/2
Answer:
x = 33/2 = 16 1/2
Step-by-step explanation:
You can clear fractions first, or you can work with the fractions as is.
(2x -7)/4 = (x +3)/3
2/4x -7/4 = 1/3x +1 . . . . . eliminate parentheses
(1/2 -1/3)x = 1 +7/4 . . . . . add 7/4 -1/3x
1/6x = 11/4 . . . . . . . . . . . simplify
x = 66/4 = 33/2 . . . . . multiply by 6, reduce the fraction
Kaitlin is saving money to buy a game. So far she has saved $12, which is two-thirds of the total cost of the game. How much does the game cost
Answers
Explanation : we would have to divide it by the fraction 2/3 to know what the total is :)
what is the graphing system of 4x - 5y = -12 and -x + 5y = 18
Answers
Answer:x= 2 y= 4
Step-by-step explanation:
look at the calculation
A 40-degree angle is translated 5 inches along a vector. What is the angle measurement, in degrees, of the Image?
Answers
Answer:
40°
Step-by-step explanation:
As clarified in an online document, a translation along a vector (which is a line in a plane) of a figure, is equivalent to a translation along a coordinate grid, and therefore, given that a translation is a form of rigid transformation, the the dimensions and inclinations of the rays forming the preimage are the same as those in the image and the angles measurement in the preimage and the image are equal.
Therefore, given that the angle measurement of the image is 40-degrees, the angle measurement of the image is also 40-degree (40°) angle.
compute the flux integral ∫sf→⋅da→ in two ways, directly and using the divergence theorem. s is closed and oriented outward
Answers
The flux integral ∫sf→⋅da→ in two ways, you can either directly evaluate the surface integral by parametrizing the surface and calculating the dot product, or use the divergence theorem by computing the divergence of the vector field and integrating it over the region enclosed by the surface.
To compute the flux integral ∫sf→⋅da→ in two ways, directly and using the divergence theorem, we first need to understand the concepts involved.
Direct computation:
In the direct method, we evaluate the surface integral directly by parametrizing the surface S and calculating the dot product between the vector field f→ and the surface normal vector da→.
Let's assume that S is a closed surface with outward orientation. To compute the flux integral directly, we need to follow these steps:
Step 1: Parametrize the surface S.
We express the surface S in terms of two parameters, typically denoted by u and v. Let's assume that S is parametrized by the functions x(u,v), y(u,v), and z(u,v).
Step 2: Calculate the surface normal vector.
Using the cross product of the partial derivatives of the parametric equations, we can determine the surface normal vector da→.
Step 3: Evaluate the dot product f→⋅da→.
Substitute the values of x, y, and z into the vector field f→, and then calculate the dot product with the surface normal vector da→. Finally, integrate this dot product over the surface S.
Using the divergence theorem:
The divergence theorem relates the flux integral of a vector field across a closed surface to the triple integral of the divergence of that vector field over the region enclosed by the surface.
The divergence theorem states that ∫sf→⋅da→ is equal to ∭V(div f→)dV, where V is the region enclosed by the surface S, and div f→ is the divergence of the vector field f→.
To compute the flux integral using the divergence theorem, follow these steps:
Step 1: Calculate the divergence of the vector field.
Compute the divergence of the vector field f→, denoted as div f→.
Step 2: Evaluate the triple integral of the divergence.
Integrate the divergence div f→ over the region V enclosed by the surface S.
The result of this triple integral will give the same value as the flux integral calculated directly.
In summary, to compute the flux integral ∫sf→⋅da→ in two ways, you can either directly evaluate the surface integral by parametrizing the surface and calculating the dot product, or use the divergence theorem by computing the divergence of the vector field and integrating it over the region enclosed by the surface. Both methods should yield the same result.
Learn more about flux here
https://brainly.com/question/29221352
#SPJ11
\($\:\:2\log _{4x}\left(x^3\right)=5\log _{2x}\left(x\right)$\)
Answers
Use the change-of-base identity to rewrite the equation as
2 log(x³) / log(4x) = 5 log(x) / log(2x)
Multiply both sides by log(4x) log(2x), noting that this is only valid if x > 0 and neither x = 1/2 nor x = 1/4 :
2 log(x³) log(2x) = 5 log(x) log(4x)
Bring down the exponent in the first logarithm:
6 log(x) log(2x) = 5 log(x) log(4x)
Move everything to one side and factorize:
6 log(x) log(2x) - 5 log(x) log(4x) = 0
log(x) (6 log(2x) - 5 log(4x)) = 0
Then either
log(x) = 0 or 6 log(2x) - 5 log(4x) = 0
In the first equation, after taking the exponential of both sides, we get
exp(log(x)) = exp(0) → x = 1
In the second equation, we have
6 log(2x) = 5 log(4x)
Expand the logarithms into sums:
6 (log(2) + log(x)) = 5 (log(4) + log(x))
6 log(2) + 6 log(x) = 5 log(4) + 5 log(x)
Simplify:
log(x) = 5 log(4) - 6 log(2)
4 = 2², so
log(x) = 5 log(2²) - 6 log(2)
log(x) = 10 log(2) - 6 log(2)
log(x) = 4 log(2)
log(x) = log(2⁴)
log(x) = log(16)
Take the exponential of both sides to get
exp(log(x)) = exp(log(16)) → x = 16
Answer:
x=1, x=16
Step-by-step explanation:
In a poll of 200 randomly selected U.S. adults, 104 said they favored a new proposition. Based on this poll, compute a 90% confidence interval for the proportion of all U.S. adults in favor of the proposition (at the time of the poll). Then complete the table below. Carry your intermediate computations to at least three decimal places. Round your answers to two decimal places. lower limit of 90%? upper limit of 90%
Answers
The lower limit of the 90% confidence interval is 0.429 when in a survey of 200 randomly chosen American adults, 104 responded in favor of the proposed proposal.
Given that
In a survey of 200 randomly chosen American adults, 104 responded in favor of the proposed proposal. Calculate a 90% confidence interval for the percentage of all U.S. adults who support the proposal based on the results of this poll (at the time of the poll). Complete the table below after that. Carry your calculations to a minimum of three decimal places.
We have to find the lower limit of 90%.
We know that
In a poll of 200 randomly selected U.S. Among adults, 104 expressed support for the novel idea.
p-hat = 104/200 = 0.52
ME = z×√[pq/n] = 2.5758×√[0.52*0.48/200] = 0.091
Now, the lower limit of the 90% confidence interval well be
p-hat-ME = 0.52-0.091 = 0.429
Therefore, The lower limit of the 90% confidence interval is 0.429 when in a survey of 200 randomly chosen American adults, 104 responded in favor of the proposed proposal.
To learn more about limit visit: https://brainly.com/question/29394831
#SPJ4
will mark brainliest ~ Select the correct answer. Which function is the inverse of f(x)= x^2 – 16 if the domain is
\(x \geqslant 0\)

Answers
Step-by-step explanation:
y = x² - 16
x² = y + 16
x = sqrt(y + 16) as x is non-negative.
Therefore f^-1(x) = sqrt(x + 16). (A)
Answer:
the answer is A
Step-by-step explanation:

can some one do this for me i will give you Brainliest

Answers
Answer:
1. 1
2. -30
3. -2
4. 15
Step-by-step explanation:
Use part 1 of the fundamental theorem of calculus to find the derivative of the function. h(x) = ex 1 8 ln(t) dt
Answers
The derivative of h(x) is zero, indicating that the function h(x) is a constant function
To find the derivative of the function h(x) = ∫[1 to 8] e× ln(t) dt using the first part of the Fundamental Theorem of Calculus, we can directly differentiate the integral with respect to x.
Let F(x) be the antiderivative of the integrand e× ln(t). By the first part of the Fundamental Theorem of Calculus, we have:
h(x) = F(8) - F(1)
To find the derivative of h(x), we differentiate both sides of the equation with respect to x:
d/dx [h(x)] = d/dx [F(8) - F(1)]
Since F(8) and F(1) are constants, their derivatives with respect to x are zero. Therefore, we have:
h'(x) = 0 - 0
Thus, the derivative of h(x) is zero, indicating that the function h(x) is a constant function.
To know more about derivative click here :
https://brainly.com/question/33102961
#SPJ4
-5 + 6a + (-8) + (-3a)=
Answers
Answer:
-5+6a+(-8)+(-3a)=
-13+3a
hope this helps
have a good day :)
Step-by-step explanation:
Answer:3a and -13
Step-by-step explanation:
hope it helps