James and Padma are on opposite sides of a 100-ft-wide canyon. James sees a bear at an angle of depression of 45 degrees. Padma sees the same bear at an angle of depression of 65 degrees.
What is the approximate distance, in feet, between Padma and the bear?
A
21. 2ft
B
75. 2ft
C
96. 4ft
D
171. 6ft
Answers
The approximate distance between Padma and the bear is 21.2 ft, which corresponds to option A.
The approximate distance between Padma and the bear, we can use trigonometry. Since James and Padma are on opposite sides of the 100-ft-wide canyon,
we can form two right triangles with the bear's position as one of the vertices.
Step 1: Determine the horizontal distance from James to the bear.
Since the angle of depression from James to the bear is 45 degrees, the horizontal distance (x) and vertical distance (y) are equal due to the properties of a 45-45-90 right triangle. Therefore, x = y. Since the canyon is 100 ft wide, x + y = 100 ft. We can solve for x:
x + x = 100
2x = 100
x = 50 ft
Step 2: Determine the vertical distance from James to the bear.
Since x = y in the 45-45-90 right triangle, the vertical distance from James to the bear is also 50 ft.
Step 3: Determine the horizontal distance from Padma to the bear.
We can now use Padma's angle of depression, 65 degrees, to find the horizontal distance (p) from Padma to the bear. Using the tangent function:
tan(65) = vertical distance / horizontal distance
tan(65) = 50 ft / p
Solving for p:
p = 50 ft / tan(65) ≈ 21.2 ft
To know more about trigonometry refer here
https://brainly.com/question/29002217#
#SPJ11
Related Questions
WILL MARK BRAINLIEST IF CORRECT

Answers
Answer:
2x - 8 = 12 has the same solution as 12/x-4 = 2
Step-by-step explanation:
They both equal 10
Part 3: Answer the following and show your solutions on the space provided.
A. Solve the following Linear equations in two variables.

Answers
The solution to the linear equation can be found to be :
x = 16y = 4How to solve the linear equation ?To solve this system of linear equations, first, we'll eliminate the fractions by finding the least common multiple (LCM) of the denominators and then multiplying each equation by the LCM.
x + 2y = 24
x + 8y = 48
Subtract equation (1) from equation (2) to eliminate x:
(8y - 2y) = (48 - 24)
6y = 24
Now, we can solve for y:
y = 24 / 6
y = 4
Now that we have y, we can substitute it into equation (1) to solve for x:
x + 2(4) = 24
x + 8 = 24
x = 24 - 8
x = 16
Find out more on linear equations at https://brainly.com/question/25858757
#SPJ1
what does a z-score tell us? question 14 options: 1) how many standard deviations an observation is from the mean. 2) the middle value if the data is in ascending order. 3) the average of a data set. 4) how many standard deviations an observation is from the median.
Answers
If X is a normally distributed random variable and X ~ N(μ, σ), then the z-score is: z = x−μ/ σ
The z-score indicates the number of standard deviations that the value x is above (right) or below (left) the mean μ. Values of x greater than the mean have positive z values, and values of x less than the mean have negative z values. The z-score of x is zero if x is equal to the mean.
The standard normal distribution is the normal distribution of standardized values called z-scores. Z-scores are measured in units of standard deviation. For example, if the normal distribution has a mean of 5 and a standard deviation of 2, then the value 11 is 3 standard deviations above (or to the right of) the mean. Here's the calculation:
x = μ + (z)(σ)
= 5 + (3)(2)
= 11
The standard normal distribution has zero mean and one standard deviation. The transformation
z= x − μ/σ
gives the distribution Z ~ N(0, 1). The value x comes from a normal distribution with mean μ and standard deviation σ.
The next two videos explain what it means to have a "normal" distributed data set.
If X is a random variable and follows a normal distribution with mean µ and standard deviation σ, the rule of thumb states within 1 standard deviation of the mean.
About 95% of the x-values lie between –2σ and +2σ of the mean µ (within two standard deviations of the mean).
About 99.7% of the x-values lie between –3σ and +3σ of the mean μ (within 3 standard deviations of the mean) .
Almost all x-values are within 3 standard deviations of the mean.
1) +1σ and -1σ have z-scores of +1 and -1 respectively.
2) +2σ and -2σ have Z-scores of +2 and -2 respectively.
3) +3σ and -3σ have Z-scores of +3 and -3 respectively.
The rule of thumb is also known as the 68-95-99.7 rule.
The exact value used to calculate the median; further decreasing the minimum value or increasing the maximum value will not change the median value. Therefore, the median does not use all the information in the data and is therefore shown to be less efficient than the mean or average, which uses all the values in the data. To calculate the average, add the observations and divide by that number.
Learn more about Standard Deviation:
https://brainly.com/question/13905583
#SPJ4
can rectangle corner perpendicular diagonal lines of the rectangle?
if so can you draw a picture
Answers
Answer:
yes
Step-by-step explanation:

Question 21 of 31
What is the length of AC?
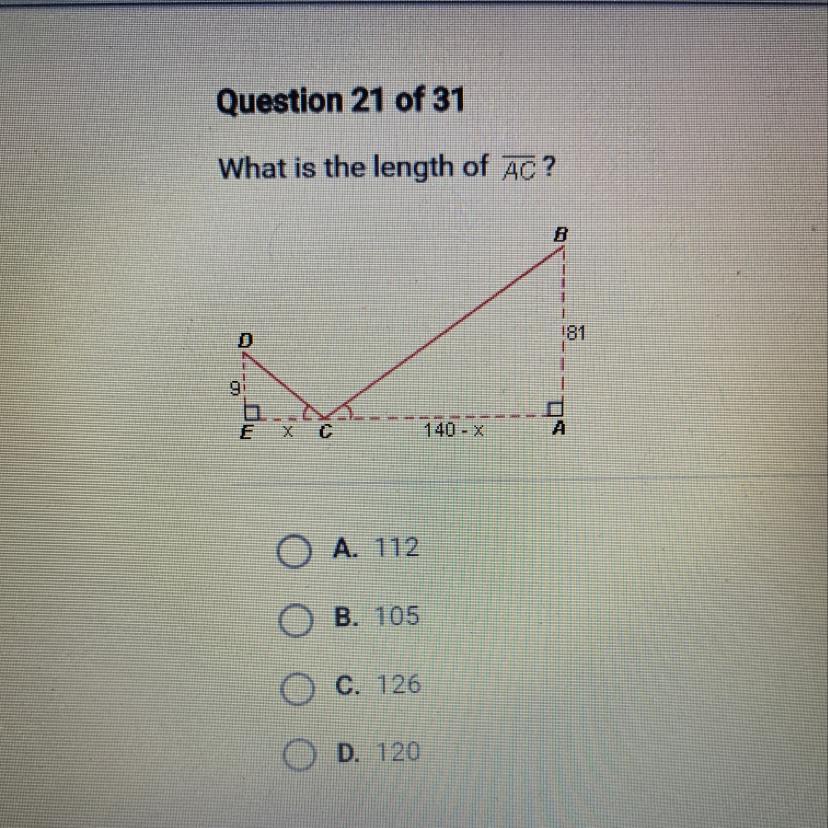
Answers
Answer:
C. 126
Step-by-step explanation:
We can use ratios to solve for corresponding side lengths.
\(\frac{140-x}{81} =\frac{x}{9}\)
Cross multiply.
\(9(140-x)=81x\)
\(140-x=9x\)
\(140=10x\)
\(14=x\)
Plug x as 14.
\(140-14=126\)
Use the table to find the products of the polynomial
pls help i’m having so much trouble with this and i don’t understand
(x^2 + x - 2)(4x^2 - 8x)

Answers
Answer:
Step-by-step explanation:
Hello,
The table is as below
\(\begin{array}{c|c|c|c} &2&1&-2\\4&\boxed{4}&\boxed{4}&\boxed{-8}\\-8&\boxed{-8}&\boxed{-8}&\boxed{16}\\\ 0&\boxed{0}&\boxed{0}&\boxed{0} \end{array}\)
It gives
\(4x^4+(4-8)x^3-(8+8)x^2+16x=4x^4-4x^3-16x^2+16x\)
Hope this helps.
Do not hesitate if you need further explanation.
Thank you
12) which of the following is factor of the polynomial x^4+x^3-x^2+x-1
x+1
x-1
Both options 1 and 2
None
please answer friends
Answers
Answer:
none
Step-by-step explanation:
If (x + h) is a factor of f(x) then f(- h) = 0
Given
f(x) = \(x^{4}\) + x³ - x² + x - 1
If (x + 1) is a factor then f(- 1) = 0
f(- 1) = \((-1)^{4}\) + (- 1)³ - (- 1)² + (- 1) - 1 = 1 - 1 - 1 - 1 - 1 = - 3 ≠ 0
Thus (x + 1) is not a factor
If (x - 1) is a factor then f(1) = 0
f(1) = \(1^{4}\) + 1³ - 1² + 1 - 1 = 1 + 1 - 1 + 1 - 1 = 1 ≠ 0
Thus (x - 1) is not a factor

severe difficulty in making mathematical calculations as a result of a brain disorder
Answers
Dyscalculia is a learning disorder that affects a person’s ability to do the math.
A learning problem called dyscalculia diminishes a person's capacity for math. Similar to how dyslexia impairs reading-related brain regions, dyscalculia interferes with the knowledge and skills connected to math and numbers. Although dyscalculia often first manifests in childhood, it can even affect adults who are unaware of it.
The signs of this condition typically emerge in childhood, particularly as kids start to master the fundamentals of math. However, many adults who suffer from dyscalculia are unaware of it. When forced to do the math, people with dyscalculia frequently experience mental health problems like anxiety, depression, and other distressing emotions.
Know more about Dyscalculia
https://brainly.com/question/29454867
#SPJ4
Find the answer to the question below
Ben deposited $6,500 in a simple interest account that pays 2.8% interest annually. If Ben leaves the money in the account for 12 years, how much interest will he earn?
Answers
Answer:
0.336?
Step-by-step explanation:
Solve the triangle. B=67∘51′,c=36m,a=74m What is the length of side b ? b=m (Round to the nearest whole number as needed.) What is the measure of angle A ? A= (Round to the nearest whole number as needed.) What is the measure of angle C ? C= (Round to the nearest whole number as needed.)
Answers
The length of side b is 56m, angle A is 45°, and angle C is 67°.
What is the length of side b in the given triangle?In the given triangle with side lengths a = 74m, b ≈ 56m, and c = 36m, the length of side b is approximately 56m.
To solve the triangle, we can use the Law of Cosines and the fact that the sum of angles in a triangle is 180 degrees. Given angle B = 67°51', we have:
Length of side b:Using the Law of Cosines, we have:
b² = a² + c² - 2ac * cos(B)
Substituting the known values:
b² = 74² + 36² - 2 * 74 * 36 * cos(67°51')
Calculating the value of b:
b ≈ √(74² + 36² - 2 * 74 * 36 * cos(67°51'))
b ≈ 55.92m (rounded to the nearest whole number, b ≈ 56m)
Measure of angle A:Using the Law of Cosines again, we have:
cos(A) = (b² + c² - a²) / (2 * b * c)
Substituting the known values:
cos(A) = (56² + 36² - 74²) / (2 * 56 * 36)
Calculating the value of A:
A = cos⁻¹((56² + 36² - 74²) / (2 * 56 * 36))
A ≈ 45° (rounded to the nearest whole number)
Measure of angle C:Using the fact that the sum of angles in a triangle is 180 degrees:
C = 180° - A - B
Substituting the known values:
C ≈ 180° - 45° - 67°51'
Calculating the value of C:
C ≈ 67°9' (rounded to the nearest whole number, C ≈ 67°)
Therefore, in the given triangle, the length of side b is approximately 56m, angle A is approximately 45°, and angle C is approximately 67°.
Learn more about the Law of Cosines
brainly.com/question/17289163
#SPJ11
express the function f(x)=1+|2x-5| in piecewise form without using absolute values

Answers
The function f(x)=1+|2x-5| in piecewise form without using absolute values will be f₁ = 4, f₂ = 2 and a = 5/2.
Given that,
f(x) = 1 + |2x - 5|
And,
f(x) = {f₁ x < a
{f₂ x ≥ a
Now,
We have,
f(x) = 1 + |2x - 5|
And,
By definition of absolute value,
|x| = {x x ≥ 0
{-x x < 0
And,
Given the absolute value,
|2x - 5|
Solve for x,
i.e.
2x - 5 = 0
We get,
x = 5/2 = 2.5
i.e.
a = 5/2
i.e.
For all values greater than x = 5/2, 2x - 5 is positive,
And,
For all values less than x = 5/2, 2x - 5 is negative.
So,
|x| = {x x ≥ 5/2
{-x x < 5/2
i.e.
|2x - 5| = {2x - 5 x ≥ 5/2
{-(2x - 5) x < 5/2
Now,
f(1) = 1 + |2(1) - 5|
We get,
f₁ = 4
And,
f(2) = 1 + |2(2) - 5|
We get,
f₂ = 2
Hence we can say that the function f(x)=1+|2x-5| in piecewise form without using absolute values will be f₁ = 4, f₂ = 2 and a = 5/2.
To learn more about absolute values click here,
https://brainly.com/question/24734454
#SPJ1
easy algebra question

Answers
Answer: 235 people got a real one
Step-by-step explanation:
The y-intercept in the linear equation y=−1/10x−2 is _[blank]_.
Enter your answer as the value that correctly fills in the blank, like this: 42
If your answer is a fraction, enter it formatted like this: 42/53
Answers
Answer:
-2 is the answer
Step-by-step explanation:
y=mx+b
b= y intercept
because it is a negative it replaces the addition sign so that it is not a positive 2.
If a rectangle has an area of 12 m?, then it has
sides of length 3 m and 4 m.
9.What are the converse, the inverse, and the
contrapositive? What are their truth values?
Answers
A conditional statement has the same truth value as Contrapositive
Here we have,
to complete the statement:
From the question, we are to determine which type of conditional statement has the same truth value as the original statement
As a general rule, if the truth value of an original statement is True, the truth value of the contrapositive would also be true
Similarly;
If the truth value of an original statement is false, the truth value of the contrapositive would also be false
Hence, a conditional statement has the same truth value as contrapositive
Read more about conditional statement at:
brainly.com/question/11073037
#SPJ1
complete question:
A conditional statement has the same truth value as:
Contrapositive
Converse
, ,
Inverse
What is the slope of the line that passes through the points
(
−
9
,
−
7
)
(−9,−7) and
(
−
11
,
−
6
)
(−11,−6)? Write your answer in simplest for
Answers
Considering the expression of a line, the equation of the line that passes through the points (-9,-7) and (-11,-6) is the equation of the line is y= -1/2x -23/2.
Linear equationA linear equation o line can be expressed in the form y = mx + b
where
x and y are coordinates of a point.m is the slope.b is the ordinate to the origin and represents the coordinate of the point where the line crosses the y axis.Knowing two points (x₁, y₁) and (x₂, y₂) of a line, the slope m of a line can be calculated as:
m= (y₂ - y₁)÷ (x₂ -x₁)
Substituting the value of the slope m and the value of one of the points in y=mx +b, the value of the "b" can be obtained.
Equation of the line in this case
Being (x₁, y₁)= (-9, -7) and (x₂, y₂)= (-11, -6), the slope m can be calculated as:
m= (-6 - (-7))÷ (-11 -(-9))
m= (-6 +7)÷ (-11 +9)
m= (1)÷ (-2)
m= -1/2
Considering point 1 and the slope m, you obtain:
-7= (-1/2)×(-9) + b
-7= 9/2 +b
-7 -9/2= b
-23/2= b
Finally, the equation of the line is y= -1/2x -23/2.
Learn more about the equation of a line having 2 points:
brainly.com/question/12851029
brainly.com/question/19496333
#SPJ1
What is the median for this list of numbers? 2, 5, 8, 9, 11, 3
Answers
Answer:
6.5
Step-by-step explanation:
for all m, n ∈ a, m r n ⇔ 5|(m2 − n2). it is a fact that r is an equivalence relation on a. use set-roster notation to list the distinct equivalence classes of r. (enter your answer as a comma-separated list of sets.)
Answers
To find the distinct equivalence classes of the relation "r," we need to determine the sets of elements in set "a" that are related to each other based on the given condition. In this case, the condition is that for any "m" and "n" in set "a," "m r n" if and only if "5|(m^2 - n^2)."
To list the distinct equivalence classes using set-roster notation, we need to identify sets of elements that are related to each other under the relation "r." Let's proceed with finding these sets:
Start by picking an arbitrary element "x" from set "a."
Identify all elements "y" in set "a" such that "x r y." In other words, find elements that satisfy the condition "5|(x^2 - y^2)."
Repeat steps 1 and 2 until all elements in set "a" have been considered.
Group all elements found in step 2 for each iteration into distinct sets.
For instance, let's assume set "a" contains the elements {1, 2, 3, 4, 5}. We will go through the steps mentioned above:
Pick 1 from set "a."
Identify elements related to 1: 1 r 4 (since 5|(1^2 - 4^2)), and 1 r 3 (since 5|(1^2 - 3^2)).
Repeat steps 1 and 2 for the remaining elements: 2 r 5 (since 5|(2^2 - 5^2)).
Group the elements found in step 2 into sets: {1, 4, 3}, and {2, 5}.
Therefore, the distinct equivalence classes of "r" are {1, 4, 3} and {2, 5}. The distinct equivalence classes of the relation "r" on set "a" are {1, 4, 3} and {2, 5}. To find the distinct equivalence classes, we need to determine sets of elements in set "a" that are related to each other under the relation "r." The relation "r" is defined as "5|(m^2 - n^2)." This means that for any elements "m" and "n" in set "a," "m r n" if and only if "5" divides the difference between the squares of "m" and "n." Using the set-roster notation, we can list the distinct equivalence classes as {1, 4, 3} and {2, 5}. These sets represent elements that are related to each other based on the given condition. To find these sets, we follow the steps outlined above. Starting with an arbitrary element from set "a," we identify all elements related to it. We repeat this process for all elements in set "a" and group the related elements into distinct sets.
The distinct equivalence classes of the relation "r" on set "a" are {1, 4, 3} and {2, 5}. These sets represent elements that are related to each other based on the given condition "5|(m^2 - n^2)."
To learn more about set-roster notation visit:
brainly.com/question/31981752
#SPJ11
14. Solve for the m<1, m<2, m<3 for the Kite.
<3 = 180 - ???
51°
Answers
The measure of angle1 and angle3 is equal that is 39° , and the measure of angle2 is 51° .
We know that , Kites have two sets of equivalent adjacent sides and one set up of congruent opposite angles.
So, the sides "AB" and "AD" are equivalent adjacent sides.
From the figure , m∠1 = 39° ,So , m∠2 = 39° ,
We see that , AC and BD are diagonals.
We also know that diagonals of kite always meet at right angles.
Let the diagonals "AC" and "BD" intersect at point O.
So , In Triangle AOB ,
⇒ m∠O + m∠1 + m∠2 = 180° ,
⇒ 90° + 39° + m∠2 = 180° ,
⇒ m∠2 = 180° - (90° + 39°) ,
⇒ m∠2 = 180° - 129° ,
⇒ m∠2 = 51°
Therefore , the required measure of angles are m∠1 = 39°, m∠2 = 51°, m∠3 = 39°.
Learn more about Kite here
https://brainly.com/question/30482906
#SPJ4
The given question is incomplete , the complete question is
Find m∠1 , m∠2 and m∠3 in the kite. The diagram is not drawn to scale.

3. Let R be the region in the first quadrant bounded by the graph of y = x2, the x-axis, and the line x = 3. Part A: Find the area of the region R. Part B: Find the value of h such that the vertical line x = h divides the region R into two regions of equal area.Previous question
Answers
The dimensions of the region bounded by the curve, y² = x, the lines, x = 1 and x = 4, and the x-axis exists the dimensions ABCD
What is meant by angle?Two straight lines or rays intersect at a same terminus to make an angle. The vertex of an angle is the point at which all points meet. The word "angle" is derived from the Latin word "angulus," which means "corner," and there are numerous types of angles depending on measurement. Acute, obtuse, right, straight, reflex, and full rotation are the names of basic angles. Two rays can be joined at their termini to form the geometric shape known as an angle.Everyone has an angle, according to cynical belief, is wisdom. Having an angle refers to operating in a way that prioritises your own needs over those of others. No one can be impartial or selfless if everyone has a point of view.Thus area of ABCD = \(\int_1^4 \mathrm{ydx} \\\)
\(& =\int_1^4 \sqrt{\mathrm{x}} \mathrm{dx} \\\)
\($& =\left[\frac{\mathrm{x}^{\frac{3}{2}}}{\frac{3}{2}}\right]_1^4 \\\)
\($& =\frac{2}{3}\left[(4)^{\frac{3}{2}}-(1)^{\frac{3}{2}}\right]\)
simplifying,
\($& =\frac{2}{3}[8-1] \\\)
Then we get,
\($& =\frac{14}{3} \text { units }\)
To learn more about angle, refer to:
https://brainly.com/question/25716982
#SPJ4

Calculate the volume of a parallelepiped whose sides are described by the vectors, A = [-4, 3, 2] cm, B = [2,1,3] cm and C= [1, 1, 4] cm, You can use the vector triple product equation Volume = A . (BXC)| .
Answers
The volume of the parallelepiped with sides given by vectors A, B and C is 13 cubic cm, which is the final answer.
The given vectors are:
A = [-4, 3, 2] cm, B = [2,1,3] cm and C= [1, 1, 4] cm
In order to calculate the volume of parallelepiped, we will use vector triple product equation:
Volume = A . (BXC)|, where BXC represents the cross product of vectors B and C.
Step-by-step solution:
We have, A = [-4, 3, 2] cm
B = [2,1,3] cm
C = [1, 1, 4] cm
Now, let's find BXC, using the cross product of vectors B and C.
BXC = | i j k| 2 1 3 1 1 4 | i j k | = -i + 5j - 3k
Where, i, j, and k are the unit vectors along the x, y, and z-axes, respectively.
The volume of the parallelepiped is given by:
Volume = A . (BXC)|
Therefore, we have: Volume = A . (BXC)
\(Volume = [-4, 3, 2] . (-1, 5, -3)\\Volume = (-4 \times -1) + (3 \times 5) + (2 \times -3)\\Volume = 4 + 15 - 6\\Volume = 13\)
Therefore, the volume of the parallelepiped with sides given by vectors A, B and C is 13 cubic cm, which is the final answer.
To know more about parallelepiped, visit:
https://brainly.com/question/30627222
#SPJ11
Verify the Pythagorean Theorem for the vectors u and v. U=(1,−1),v=(1,1) Are u and v orthogonal? Yes No Calculate the following values. ∥u∥2=∥v∥2=∥u+v∥2= We draw the following conclusion. We have verified that the conditions of the Pythagorean Theorem hold for these vectors
Answers
By verifying the Pythagorean Theorem for the vectors u and v,
∥u∥²= 2
∥v∥²= 2
∥u+v∥²= 8
u and v are not orthogonal.
We have verified that the conditions of the Pythagorean Theorem hold do not for these vectors.
To verify the Pythagorean Theorem for the vectors u and v, we need to calculate the norm of each vector and the norm of their sum.
The norm of u is √(1² + (-1)²) = √(2).
The norm of v is √(1² + 1²) = √(2).
The norm of u+v is √((1+1)² + (-1+1)²) = √(4) = 2.
Then, we can check if the Pythagorean Theorem holds by verifying if ||u+v||² = ||u||² + ||v||²:
||u||² + ||v||² = 2 + 2 = 4.
||u+v||² = 4.
Therefore, ||u+v||² = ||u||² + ||v||², and we can conclude that the Pythagorean Theorem holds for these vectors. Additionally, since the dot product of u and v is zero (1 × (-1) + 1 × (-1) = -2 + (-1) = -3), we can confirm that u and v are orthogonal.
Learn more about the Pythagorean Theorem at
https://brainly.com/question/14930619
#SPJ4
The question is -
Verify the Pythagorean Theorem for the vectors u and v.
U=(1,−1), v=(1,1)
Are u and v orthogonal?
Yes
No
Calculate the following values.
∥u∥²=
∥v∥²=
∥u+v∥²=
We draw the following conclusion.
We have verified that the conditions of the Pythagorean Theorem hold _____ (do/do not) for these vectors.
ANNNSWER PLZ 20 c rule

Answers
Answer:
No solutions
Step-by-step explanation:
Let's solve your equation step-by-step.
5m−2(m+3)+6/2
=3m−4/2
Step 1: Simplify both sides of the equation.
5m−2(m+3)+6/2
=3m−4/2
5m+(−2)(m)+(−2)(3)+6/2
=3m+−2(Distribute)
5m+−2m+−6+3=3m+−2
(5m+−2m)+(−6+3)=3m−2(Combine Like Terms)
3m+−3=3m−2
3m−3=3m−2
Step 2: Subtract 3m from both sides.
3m−3−3m=3m−2−3m
−3=−2
Step 3: Add 3 to both sides.
−3+3=−2+3
0=1
Answer:
There are no solutions
Answer:
No solutions
Step-by-step explanation:
\(5m-2(m+3)+\frac{6}{2} =3m-\frac{4}{2}\)
\(5m-2m-6+\frac{6}{2} =3m-\frac{4}{2}\)
\(5m-2m-6+3 =3m-2\)
\(5m-2m-3 =3m-2\)
\(3m-3 =3m-2\)
\(3m-3+3 =3m-2+3\)
\(3m=3m+1\)
\(3m-3m =3m- 3m+1\)
0 = 1
No solutions
What is the measure of angle x? A 58°B. 38°C 42° D. 28°

Answers
Answer:
B. 38°
Explanation:
From the given figure, angles x and 142 degrees are on a straight line.
The sum of angles on a straight line is 180 degrees, therefore:
\(x+142\degree=180\degree\)Next, we solve the equation for x:
\(\begin{gathered} x=180\degree-142\degree \\ x=38\degree \end{gathered}\)The correct choice is B.
Answer: i don't care
Step-by-step explanation: I am doing it for the points
sry for not knowing the answer
Hi can someone please help me


Answers
Answer:
Below
Step-by-step explanation:
f(b) = population in 2015 = 39.1
f(a) = population in 2010 = 36.5
b-a is 2015 - 2010 = 5 yrs
plug in the values (39.1 - 36.5) / 5 = .52 million ppl / year
What value of will make the triangles similar by the similarity theorem?
Answers
As similarity theorem, the value of x that will make the triangles similar by SSS similarity theorem is 77.
Similarity theorem:
In math, similarity theorem refers the line segment splits two sides of a triangle into proportional segments if and only if the segment is parallel to the triangle's third side.
Given,
Here we need to find the t value of will make the triangles similar by the similarity theorem.
For example, we are told that the 2 triangles are similar by SSS theorem.
Here we know that, SSS means Side - Side -Side and it is a congruence theorem which states that the 3 corresponding sides of two triangles have same ratio, then we can say that the two triangles are congruent by SSS theorem
Therefore, in the triangles ,applying the SSS postulate gives;
=> x/35 = 44/20
Then by applying the multiplication property of equality, let us multiply both sides by 35 to get;
=> x = (44 * 35)/20
When we simplify this one then we get,
=> x = 77
Therefore, the value of x is 77.
To know more about Similarity theorem here.
https://brainly.com/question/24167205
#SPJ4
Factor 6x + 3y
I don't remember how to do this
Answers
Answer:
3(2x+y)
Step-by-step explanation:
3 is the gcf. So it would be 3(2x+y)
The diameter of ball bearing are ditributed normally. The mean diameter i 81 millimeter and the variance i 16. Find the probability that the diameter of a elected bearing i greater than 85 millimeter. Round your anwer to four decimal place
Answers
the probability that the diameter of a elected bearing is greater than 85 millimeter P(diameter > 85) = P(z > (85-81)/4) = P(z > 1) = 0.1587
The diameter of ball bearings is normally distributed, with a mean of 81 millimeters and a variance of 16.
To calculate the probability that a selected bearing has a diameter greater than 85 millimeters, we first calculate the z-score for 85 millimeters.
We subtract 81 from 85 to get 4, and divide by 4 to get 1 for the z-score.
We the look up the probability for a value of 1 in the z-table, which is 0.1587.
This is the probability that a selected bearing has a diameter greater than 85 millimeters, rounded to four decimal places.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
how do i solve 7x^{2} +11y^{2} =40
Answers
Answer:
Step-by-step explanation:
There is no solution as you have two variables and only one equation. The best you can do is solve for one variable as a function of the other.
\(7x^2+11y^2=40\\ \\ 11y^2=40-7x^2\\ \\ y^2=\frac{40-7x^2}{11}\\ \\ y=\sqrt{\frac{40-7x^2}{11}}\)
a 10 meter ladder is placed against the wall the base of the ladder is 2m from the wall how far up the wall does the ladder reach
Answers
Answer:20
Step-by-step explanation:hope this helps you
Michael is trying to determine where to open two new store locations. He has population data to determine the amount of revenue he will receive for each location. He is charged a \( \$ 1000 \) fee for
Answers
Michael needs to analyze the population data, demographics of the city, and the competition in the area to determine whether or not to open a new store.
Michael is trying to determine where to open two new store locations. He has population data to determine the amount of revenue he will receive for each location.
He is charged a $1000 fee for opening a new store at a certain location. However, he is unsure whether the population of the city would be large enough to warrant opening a new store at that location.
The first step that Michael needs to take is to analyze the population data that he has.
Based on the population data, he needs to make an informed decision about whether or not to open a new store at that location. This would require him to take into consideration the average income of the population as well as the demographics of the city.
Another important factor that Michael needs to take into consideration is the competition in the area. If there are already several stores in the area, then opening a new store might not be a good idea.
This is because the competition would be too high and he would not be able to generate enough revenue to make up for the cost of opening a new store.
However, if there are no stores in the area, then Michael might consider opening a new store. This would require him to invest a significant amount of money, but he could also generate a significant amount of revenue in return.
Additionally, he needs to take into consideration the cost of opening a new store and whether or not he can generate enough revenue to make up for that cost.
Overall, Michael needs to carefully analyze all the data that he has before making an informed decision about where to open new store locations.
In conclusion, Michael needs to analyze the population data, demographics of the city, and the competition in the area to determine whether or not to open a new store. If the population is large enough and there is no competition in the area, then he should consider opening a new store. However, if there is already a significant amount of competition in the area, then he should avoid opening a new store.
To know more about demographics visit:
brainly.com/question/32805670
#SPJ11