John is 1.6 m tall. robbin is 156 cm tall what is the ratio of johns' height to robbins height?
Answers
Answer:
johnns height 4cm to Robin's height
The ratio of John's height to Robin's height is 20:19.
To find the ratio of John's height to Robin's height, we need to convert their heights to the same unit of measurement. Let's convert Robin's height from centimeters to meters:
Robin's height = 156 cm = 156/100 m = 1.56 m
Now that both heights are in meters, we can calculate the ratio:
John's height: Robin's height = 1.6 m : 1.56 m
To simplify the ratio, we can divide both heights by the same value:
1.6 m : 1.56 m = (1.6/0.08) m : (1.56/0.08) m = 20 : 19
Therefore, the ratio of John's height to Robin's height is 20:19.
To know more about ratios:
https://brainly.com/question/29254296
#SPJ6
Related Questions
Let R be a ring with identity.
(a) Let u be a unit in R. Define a map iu :R map to R by r map to uru-1. Prove that iu is an automorphism of R. Such an automorphism of R is called an inner automorphism of R. Denote the set of all inner automorphisms of R by Inn(R).
(b) Denote the set of all automorphisms of R by Aut(R). Prove that Inn(R) is a normal subgroup of Aut(R)
(c) Let U(R) be the group of units in R. Prove that the map
phi: U(R) maps to Inn(R)
defined by u maps to iu is a homomorphism. Determine the kernel of phi.
(d) Compute Aut(Z), Inn(Z), and U(Z).
Answers
(a) The set of all inner automorphisms of R is denoted by Inn(R).
(b) Inn(R) is a normal subgroup of Aut(R).
(c) \($\phi(uv)=\phi(u)\circ \phi(v)$\) for all \($u,v\in \text{U}(R)$\), which shows that \($\phi$\).
(d) \(Aut(\mathbb{Z}) \cong {\pm 1}$, $Inn(\mathbb{Z}) \cong {\mathrm{id}_\mathbb{Z}}$, and $U(\mathbb{Z}) \cong {1,-1}$.\)
What is subgroup?
In abstract algebra, a subgroup is a subset of a group that satisfies the same group axioms as the parent group.
(a) Let u be a unit in R. We need to show that the map \($iu:R\to R$\) defined by \($r\mapsto uru^{-1}$\) is an automorphism of R, i.e., it is a bijective ring homomorphism.
First, note that \($iu$\) is a ring homomorphism since \($iu(ab)=uaubu^{-1}=iu(a)iu(b)$\) and \($iu(a+b)=uau^{-1}+ubu^{-1}=iu(a)+iu(b)$\) for all \($a,b\in R$\).
To show that \($iu$\) is injective, suppose that \($iu(a)=iu(b)$\) for some \($a,b\in R$\). Then \($ua u^{-1}=ub u^{-1}$\), so \($a=b$\). Thus, \($iu$\) is injective. To show that \($iu$\) is surjective, let \($r\in R$\) be arbitrary. Then \($iu(u^{-1}ru)=ru$\), so \($ru=iu(u^{-1}ru)\in \text{Im}(iu)$\). Thus, \($iu$\) is surjective. Therefore, \($iu$\) is a bijective ring homomorphism, and hence it is an automorphism of \($R$\). Such automorphisms are called inner automorphisms of R. The set of all inner automorphisms of R is denoted by Inn(R).
(b) To show that Inn(R) is a normal subgroup of Aut(R), we need to show that \($gig^{-1}\in \text{Inn}(R)$\) for all \($g\in \text{Aut}(R)$\) and \($i\in \text{Inn}(R)$\). Let \($g\in \text{Aut}(R)$\) and \($i_u\in \text{Inn}(R)$\), where u is a unit in R. Then for any \($r\in R$\), we have
\(g(i_u(r))&=g(ur u^{-1})\&=g(u)g(r)g(u^{-1})\&=(gu)(r)(gu)^{-1}\&=i_{gu}(r).\)
Thus, \($g(i_u(r))=i_{gu}(r)$\) for all \($r\in R$\), which implies that \($gig^{-1}=i_{gu}\in \text{Inn}(R)$\). Therefore, Inn(R) is a normal subgroup of Aut(R).
(c) Let U(R) be the group of units in R. We need to show that the map \($\phi: \text{U}(R)\to \text{Inn}(R)$\) defined by \($\phi(u)=i_u$\) is a homomorphism and determine its kernel. To show that \($\phi$\) is a homomorphism, let \($u,v\in \text{U}(R)$\). Then for any \($r\in R$\), we have
\(\phi(uv)(r)&=i_{uv}(r)\\\\&=(uv)r(uv)^{-1}\\\\&=u(vru^{-1})u^{-1}\\\\&=u(i_v(r))u^{-1}\\\\&=(i_u\circ i_v)(r)\\\\&=(\phi(u)\circ \phi(v))(r).\)
Thus, \($\phi(uv)=\phi(u)\circ \phi(v)$\) for all \($u,v\in \text{U}(R)$\), which shows that \($\phi$\).
(d) We have \(Aut(\mathbb{Z}) \cong {\pm 1}$, $Inn(\mathbb{Z}) \cong {\mathrm{id}_\mathbb{Z}}$, and $U(\mathbb{Z}) \cong {1,-1}$\).
To see why \($Aut(\mathbb{Z}) \cong {\pm 1}$\), note that any automorphism of \($\mathbb{Z}$\) is determined by the image of 1. If \($f:\mathbb{Z}\to\mathbb{Z}$\) is an automorphism of \($\mathbb{Z}$\), then \($f(1)$\) must be an integer \($\pm 1$\), since f preserves the additive and multiplicative structure of \($\mathbb{Z}$\). Therefore, the map \($f\mapsto f(1)$\) is an isomorphism from \(Aut(\mathbb{Z})$ to ${\pm 1}$\).
Since \($\mathbb{Z}$\) is commutative, any inner automorphism of \($\mathbb{Z}$\) is the identity map. Therefore, \($Inn(\mathbb{Z}) \cong {\mathrm{id}_\mathbb{Z}}$\).
Finally, \($U(\mathbb{Z}) = {\pm 1}$\), since the only units in \($\mathbb{Z}$\) are \($1$\) and \($-1$\).
To learn more about subgroup visit:
https://brainly.com/question/30865357
#SPJ4
What is the amplitude of g(x)=8cos(5πx+3π/2)-9
Answers
Answer:
8
Step-by-step explanation:
The value of the amplitude is always positive and it tends to be number in front of the cosine function so for example by using the form 'a.cos(bx - c) + d', we can know that the amplitude is the number in front of the function so its 'a'
Solve each equation. Check your answer. 43-3 d=d+9
Answers
d= 17/2 is the solution of the given equation 43-3 d=d+9.
According to the given question.
We have a linear equation in one variable 43 -3d = d + 9.
Since, we have to solve the above linear equation in one varible 43 -3d = d + 9, which means we have to solve the above equation for d.
As we know that, the linear equations in one variable is an equation which is expressed in the form of ax+b = 0, where a and b are two integers, and x is a variable and has only one solution.
Thereofore, the solution of the given linear equation in one variable 43 -3d = d + 9 is given by
43 -3d = d + 9
⇒ 43 - 9 -3d = d (subtracting 9 from both the sides)
⇒ 34 = d + 3d (adding 3d both the sides)
⇒ 34 = 4d
⇒ d = 34/4
⇒ d = 17/2
Now, we will check whether d = 17/2 is the solution of the given equation or not.
Thereofore,
LHS
= 43 - 3(17/2)
= 43 - 51/2
= 86 - 51/2
= 35/2
RHS
= 17/2 + 9
= 17 + 18/2
=35/2
Here, LHS = RHS for d = 17/2
Hence, d= 17/2 is the solution of the given equation 43-3 d=d+9.
Find out more information about equation here:
https://brainly.com/question/28595319
#SPJ4
You went shopping for back to school and bought packs of pens and pencils. a pack of
pencils cost $2.50 and a pack of pens cost $3. you spent a total of $35 and bought a
total of 13 packs. how many packs of pencils and how many packs of pens did you
buy?
Answers
Answer:
5 packs of pens and 8 packs of pencils.
Step-by-step explanation:
Let the Pn and Pl stand for the number of packs of pens (Pn) and pencils (Pl) purchased.
We know that each pack of pens is $3 and each pack of pencils is $2.50.
We are also told that Pn + Pl = 13 [In total, 13 packs were purchased].
And we're told that $35 was spent.
The $35 must equal: $3*Pn + $2.5*Pl [the sum of the number of packs of each times the price per pack for each]
3*Pn + 2.5*Pl = 35
Rearrange the first equation:
Pn + Pl = 13
Pn = 13 - Pl
Use this definition of Pn in the second equation:
3*Pn + 2.5*Pl = 35
3*(13 - Pl) + 2.5*Pl = 35
39 - 3Pl + 2.5Pl = 35
-0.5Pl = -4
Pl = 8
8 packs of pencils (Pl) were purchased.
This means the packs of pens purchased must be 5, since a total of 13 packs were purchased.
Check:
Does 5 packs of pens and 8 packs of pencils total $35?
5*($3) + 8*($2.5) = $35 ??
$15 + $20 = $35 ?
YES
You bought 5 packs of pens and 8 packs of pencils.
how many bit strings contain exactly eight 0s and 10 1s if every 0 must be immediately followed by a 1?
Answers
There are 450 bit strings that contain exactly eight 0s and ten 1s, with every 0 immediately followed by a 1.
Which bit strings contain exactly eight 0s and 10 1s in case every 0 followed by a 1?Calculate the number of bit strings that contain exactly eight 0s and ten 1s, without any restrictions.
The total number of bit strings of length 18 that contain exactly eight 0s and ten 1s can be calculated using the binomial coefficient formula:
${18 \choose 8} = \frac{18!}{8!10!} = 43758$Adjust for the restriction that every 0 must be immediately followed by a 1.
If every 0 must be immediately followed by a 1, then we can consider the 0s and 1s as pairs. We have eight 01 pairs and two extra 1s. The 01 pairs can be arranged in ${10 \choose 8} = 45$ ways
The two extra 1s can be placed in any of the remaining 10 positions. Thus, the total number of bit strings that contain exactly eight 0s and ten 1s, with every 0 immediately followed by a 1, is:
$45 \times 10 = 450$Learn more about Expression
brainly.com/question/28172855
#SPJ11
Store a sells fabric for 3.00 per yard Store b sells packages of fabric for 3.00 The cost of fabric at either can be modeled by the function c(t)=3t where t is the number of yards of fabric at store a and t is the number of packages of fabric at store b The domain of c(t)=3t is all real numbers
Answers
Answer:
\(0 \le t < \infty\)
Step-by-step explanation:
Given
\(c(t) = 3t\)
Required
The domain
From the question, we understand that t represents number of yards/packages (depending on the store)
This means that:
\(t \ge 0\) ---- the start value
\(t < \infty\) --- the end value
Rewrite \(t \ge 0\) as \(0 \le t\)
So, we have: \(0 \le t\) and \(t < \infty\)
Hence, the domain is: \(0 \le t < \infty\)
At the start of the week, Apple's stock price was $32. That week, the value of the stock gained $1.25, and then lost $5.50, lost another $2, gained $3.25 and lost $1.75.
Part A: What was the value of the stock at the end of the week?
Answers
Answer:
$27.25
Step-by-step explanation:
When there is a gain, that is a positive amount, so add the positive numbers together.
1.25 + 3.25 = 4.50
When there is a loss, that is a negative amount, so add the negatives together.
-5.50 + (-2.00) + (-1.75) = -9.25
Add stock price and the positive amount
32.00 + 4.50 = 36.50
Now add (subtract since you have a negative and a positive amount) the negative amount.
36.50 + (-9.25) = 27.25
Which set or subset does -12.75 belong to
Answers
-12.75 belongs to the set of Rational numbers.
A rational number is a number that can be expressed as the quotient or fraction frac p q of two integers, a numerator p
and a non-zero denominator q.
Rational numbers are numbers that can be expressed as a fraction of two integers (p/q), where q is not equal to zero.
Identify the number: -12.75
Determine if it can be expressed as a fraction of two integers: -
12.75 can be written as -51/4, which are both integers.
Confirm that the denominator (q) is not equal to zero:
In this case, q = 4, which is not equal to zero.
Therefore, -12.75 belongs to the set of Rational numbers.
for such more question on Rational numbers
https://brainly.com/question/19079438
#SPJ11
Find the measure of angle y, given that EF || CB.
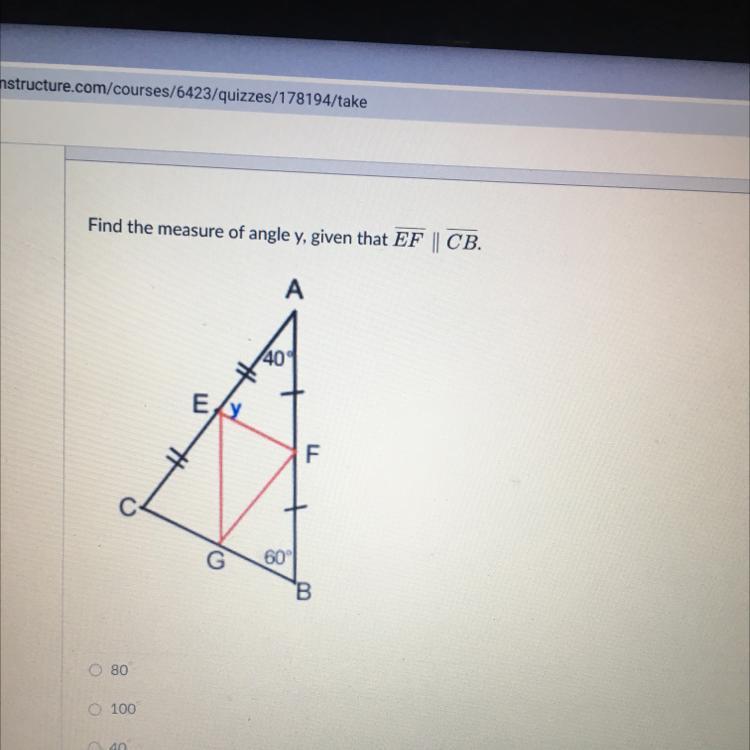
Answers
Answer:
y = 80
Step-by-step explanation:
∵EF║CB
∴∠AFE = ∠FBG = 60°
∠AEF = y = 180 - (40 + 60) = 80°
Answer:
Step-by-step explanation:
∠A + ∠B + ∠C = 180 {Angle sum property of triangle}
40 + 60 + ∠c = 180
100 + ∠C = 180
∠C = 180 - 100
∠C = 80
EF // CB and CE is transversal
y = ∠C {corresponding angles are congruent}
y = 80°
You buy 3.19 pounds of oranges, 1.45 pounds of peaches, and 1.88 pounds of apples. What is your total bill?
Answers
Answer i dont know the amount of the items
Step-by-step explanation:
give us the amount of them please
In ΔWXY, x = 4.7 cm, y = 7.9 cm and ∠W=162°. Find the area of ΔWXY, to the nearest 10th of a square centimeter.
Answers
The area of the triangle to the nearest tenth is 5.8cm²
What is area of a triangle?A triangle is a closed, 2-dimensional shape with 3 sides, 3 angles, and 3 vertices. A triangle is also a polygon. Examples of triangle include, isosceles, equilateral , scalene e.t.c
The area of a triangle is expressed as;
A = 1/2 b h for right angle triangle and A = absinC for others.
Here; x = 4.7, y = 7.9, W = 162
area = 1/2× 4.7 × 7.9 sin162
= 1/2 × 4.7 × 7.9 × 0.31
= 5.8 cm²( nearest tenth)
Therefore the area of the triangle is 5.8cm²
learn more about area of triangle from
https://brainly.com/question/17335144
#SPJ1
Find the value of x. Write your answer in simplest form.
8/2
The value of x is

Answers
Answer:
the value of x is 8
Step-by-step explanation:
the catheters were equal to each other
7
Find the area of the following trapezoid.
14
7
5
Answers
Answer: 66.5 u^2
Step-by-step explanation:
Which of the following is the equation of a parabola with the focus at (0, 3/4) and the directrix y = -3/4?
Answers
Answer:
do you have the picture I actually understand it if I see it in pictures .
Which is the first step in solving
X-2 = 2?
Answers
Answer:
The first step is to find a number that when subtracted from 2 gives you 2.
Step-by-step explanation:
The algebraic part of this problem would be to add the -2 (adding 2 to both sides) to both sides, so
first x-2=2, then x-2(+2)=2(+2) which would give us,
x=4
*note: the parenthesis are just to show that we are adding the 2, to make it more understandable.
3/4 x 5
Multiply this
Answers
Answer:
15/4 or 3.75.
Step-by-step explanation:
Multiply the numbers as you would in regular math to get 3x5=15. leaving you with 15/4.
Write the equation of a line parallel to y = 2x + 3 that passes through the point (3,1)
Answers
Answer:
Step-by-step explanation:

Answer:
y = 2x-5
Step-by-step explanation:
Lets look for an equation in the standard form of y=mx+b, where m is the slope and b the y-intercept (the value of y when x=0).
A reference line is given: y=2x+3. It has a slope of 2. Parallel lines have the same slope, so the line we are looking for will also have a slope of 3. We can therefore wrtite what we know sio far. The new line will be:
y = 2x+b
Any vale of b will produce a line that is parallel to the referenc elien. But we need a line that goes through a given point of (3,1). By choosingf the correct value of b, we can force the line therough this point. The easiest way to find b is to use the known point in the equiation we have thuis far, and solve for b:
y = 2x+b
1 = 2*(3)+b for (3,1)
b = -5
The equation of a line parallel to y=2x+3 and going through point (3,1) is:
y = 2x-5
See attached graph.

Just to need solve this asap
which value represents (A u B)
pls don't answer randomly for points

Answers
Answer: 55
Step-by-step explanation:
Given
Values are presented in the Venn diagram
No of left-handed students \(n(A)=25\)
No of vegetarians students \(n(B)=45\)
Students who are left-handed and vegetarian is given by \(n(A\cap B)=15\)
\(n(A\cup B)\) is given by \(n(A\cup B)=n(A)+n(B)-n(A\cap B)\)
Put the values
\(n(A\cup B)=25+45-15\\n(A\cup B)=55\)
Find the equation of the line through point (−2,−1) and perpendicular to 5x+6y=−6.
Answers
Step-by-step explanation:
When lines are perpendicular to each other
multiplying their gradients(m) will equal to - 1
so , m1 × m2 = -1
1st:Find m1
5x+6y= -6
make y the subject,
6y= -5x -6
\(y = \frac{ - 5x - 6}{6} \)
y= -5/6x - 1
because y = mx + c
m1 = -5/6
2nd:find m2
-5/6 × m2 = -1
m2 = 6/5
3rd: substitute m2 and the coordinates into y=mx+c
y=mx+c
-1= (6/5)(-2)+c
-1 = -12/5 + c
-5 = -12 + c
-5+12= c
c = 7
4th: substitute m2 and c into y= mx+c to find the equation the line
y =6/5x + 7 (Ans)
As per slope-intercept form, the equation of the line through point (−2,−1) and perpendicular to 5x + 6y = -6 is 5y = 6x + 7.
What is the slope-intercept form of a straight line?The slope-intercept form of a straight line is y = mx + c.
Here, 'm' is the slope and 'c' ix the y-intercept of the given line.
The given equation is 5x + 6y = - 6
Therefore, in slope-intercept form, this equation will be:
y = - 5x/6 - 1
Therefore, the slope of this line is m = - 5/6 and the y-intercept is c = - 1.
The required line is perpendicular to the given line.
Therefore, the slope of the required line is
= - 1/m
= 6/5
Again, the required line passes through the point (- 2, - 1).
Therefore, - 1 = - 2(6/5) + c
⇒ c = - 1 + 12/5
⇒ c = 7/5
The equation of the required line is
y = (6/5)x + 7/5
⇒ 5y = 6x + 7
Learn more about the slope-intercept form of a straight line here: https://brainly.com/question/14534555
#SPJ3
1 Fifty-five students, 4 teachers, and 3
parent helpers will go on a trip to a
planetarium this Friday. If each student
brings $12 and each adult brings $22, how
much money will they bring all together?
For my little cousin
Answers
(5) Compute the frequency mode for following distribution. Size of item 0-4 4-8 8-12 12-16 -16-20 20-24 24-28(frequency } 5 ,7, 9 ,14, 12, 10 ,6
Answers
The frequency mode for the given distribution is the class interval 12-16.
To compute the mode for the given frequency distribution, we need to find the class interval with the highest frequency.
The distribution is as follows:
Size of Item: 0-4 4-8 8-12 12-16 16-20 20-24 24-28
Frequency: 5 7 9 14 12 10 6
We can see that the class interval with the highest frequency is 12-16, which has a frequency of 14.
Therefore, the mode of this frequency distribution is the class interval 12-16.
The mode represents the value or interval that occurs most frequently in a data set.
In this case, the class interval 12-16 has the highest frequency of 14, which is greater than the frequencies of other class intervals.
It's important to note that in some cases, a distribution may have more than one mode if multiple intervals have the same highest frequency. However, in this given frequency distribution, the class interval 12-16 is the only mode as it has the highest frequency among all intervals.
Thus, the frequency mode for the given distribution is the class interval 12-16.
For similar question on frequency mode.
https://brainly.com/question/31530115
#SPJ8
Oil spilled from a ruptured tanker spreads in a circle whose area increases at a constant rate of 8.5 mi^2/hr. How rapidly is radius of the spill increasing when the area is 7 mi^2?
Answers
To find the rate at which the radius of the oil spill is increasing when the area is 7 mi^2, dr/dt ≈ 0.203 mi/hr the area of the spill is 7 mi^2, dr/dt ≈ 0.203 mi/hr the radius is increasing at a rate of 0.203 mi/hr.
Where A is area and r is the radius. Taking the derivative of both sides with respect to time, we can express the rate of change of the area as dA/dt = 2πr(dr/dt). Given that dA/dt is constant at 8.5 mi^2/hr, we can substitute the values to find the rate at which the radius is increasing.
We have the equation dA/dt = 2πr(dr/dt), where dA/dt represents the rate of change of the area, r is the radius, and dr/dt is the rate at which the radius is changing. We are given that dA/dt is constant at 8.5 mi^2/hr. When the area is 7 mi^2, we can substitute these values into the equation: 8.5 = 2π(7)(dr/dt)
Simplifying the equation, we can solve for dr/dt: dr/dt = 8.5 / (2π(7)) Evaluating the expression, we find: dr/dt ≈ 0.203 mi/hr
Therefore, when the area of the spill is 7 mi^2, the radius is increasing at a rate of approximately 0.203 mi/hr.
To learn more about radius click here : brainly.com/question/13449316
#SPJ11
A television costs $400,00 cash. When bought on hire purchase, a deposit 1 point
of $60.00 is required with 12 equal monthly installments of $42.50. How
much is saved by paying cash?
O A. $60.00
O B. $80.00
O C. $110.00
O
D. $170.00
Answers
$42.50 x 12 months = $510 + the $60.00 deposit is $570. You subtract $570-400 and you get $170.
On December 13, 2007, one British pound was worth 2.04 U.S. dollars.(a)On that date, how many pounds was 56.65 dollars worth?Round your answer to the nearest hundredth of a pound.pounds(b)On that date, how many dollars was 163.23 pounds worth?Round your answer to the nearest hundredth of a dollar.dollars
Answers
On December 13, 2007, 56.65 dollars is worth 27.77 pounds.
On December 13, 2007, 163.23 pounds is worth 332.99 dollars.
The exchange rate of a currency is the rate at which one currency is exchanged for another currency. There are usually two pairs of currency in an exchange rate. The exchange rate given in these question is: 1 pound = 2.04 dollars. This means that 1 pound would buy 2.04 dollars.
In order to determine the value of pounds given the value of the dollars, this formula would be used:
Value in pounds = value of dollars / exchange rate
56.65 / 2.04 = 27.77 pounds
In order to determine the value of dollars given the value of pounds, multiply the given value of dollars by the exchange rate.
Value in dollars = value of pounds x exchange rate
163.23 x 2.04 = 332.99 dollars
A similar question was answered here: https://brainly.com/question/19437632?referrer=searchResults
Yolanda drove 605 miles in 11 hours.
At the same rate, how long would it take her to drive 495 miles?

Answers
Answer:
So it would take Yolanda 9 hours to drive 495 miles at the same rate.
Step-by-step explanation:
To solve this problem, we can use the formula: distance = rate x time.
We know that Yolanda's rate of driving is 605 miles in 11 hours, so we can find her average speed by dividing the distance by the time:
rate = distance / time
rate = 605 miles / 11 hours = 55 miles per hour
Now that we know Yolanda's average speed, we can use it to find the time it would take her to drive 495 miles at that rate:
time = distance / rate
time = 495 miles / 55 miles per hour = 9 hours
Divide
5445/605
So it took 9 hours
9
A company buys a digital scanner for $12,000 the value of the scanner is $12,000 (1-n/5) after n years. The company has budget to replace the scanner when the trade-in value is 2400. After how many years should the company plan to replace the machine in order to receive this trade in value?
Answers
For the given distance the time taken for the company plan to replace the machine in order to receive this trade in value is 4 years.
The term called distance is defined as the two points lie on the same horizontal or same vertical line and it is the distance can be found by subtracting the coordinates that are not the same.
Here we have know that the company buys a digital scanner for $12,000 the value of the scanner is $12,000 (1-n/5) after n years.
And here we also know that the company has budget to replace the scanner when the trade-in value is 2400.
By Using the given expression for the value of scanner after n years, we equate it to $2400 and solve for n is written as,
=> 12000 (1 - n/5) = 2400
When we simplify this one then we get,
=> 1 - n/5 = 2400/12000
=> 1 - n/5 = 0.2
=> n/5 = 0.8
=> n = 4.
To know more about distance here.
https://brainly.com/question/4199102
#SPJ4
10 + 3k = 22
answers:
a. 12
b. no answer text provided
c. 6
d. 4
Answers
Answer:
D. 4Step-by-step explanation:
10 + 3k = 22
3k = 22 - 10
k = 12 / 3
k = 4
therefore, the answer is D. 4
Write the equation of a quadratic function whose graph has x-intercepts at x=3 and x=-4 and a y-intercept at 48.
Answers
Answer:
Step-by-step explanation:
okay i will answer but i dont see the question
What was the most goals the team scored in a game?

Answers
The most goals the team scored in a game is 8
What was the most goals the team scored in a game?From the question, we have the following parameters that can be used in our computation:
The box plot
The most goals the team scored in a game is the maximum of the box plot
From the box plot, we have
Maximum = 8
Using the above as a guide, we have the following:
Most goal = 8
Hence, the most goal is 8
Read more about boxplot at
https://brainly.com/question/3473797
#SPJ1
Answer and I will give you brainliest.
A cat can travel a distance of 32.5 meters in 13 seconds. What is the average speed of the cat to the nearest hundredth of a m/s? *
A 2.5 mph
B 0.4 mph
C 2.5 m/s
D 0.4 m/s
Answers
Answer:
D: 0.4 m/s
Step-by-step explanation:
32.5 in 13 sec
32.5/32.5=1
so
13/32.5 would be the answer
1 meter in 0.4
Answer:
C
Divide 32.5 with 13, because m/s means meters divide by seconds
im not sure tho