John is going to start saving $20 every month to buy a new IPod. His parents gave him $10 for his birthday to open his savings account. The equation y = 20x + 10 represents John’s savings account balance x months after be began saving.
a) How many months will it take John to save enough money for the $300 IPod? Explain.
b) If John saved $40 per month instead of $20, how would you expect the slope of the graph to change? Explain.
Answers
Answer A: It would take fifteen months, or one year and three months, to get three hundred dollars.
Answer B: It would take seven and a half months to get three hundred dollars at this rate. It would also change the slope by making it go down more.
Step-by-step explanation:
Three hundred divided by twenty equals fifteen, which represents the amount of months.
If you do the same thing with the other ratio, but change twenty to forty, you get seven and a half.
Have a nice day!
a) The number of months for the saving of $300 will be 14¹/₂.
b) The slope of the saving of $40 will be y = 40 x + 10
What is an equation of the line?An equation of the line is defined as a linear equation having a degree of one. The equation of the line contains two variables x and y. And the third parameter is the slope of the line which represents the elevation of the line.
The general form of the equation of the line:-
y = mx + c
m = slope
c = y-intercept
Slope = ( y₂ - y₁ ) / ( x₂ - x₁ )
Given that John is going to start saving $20 every month to buy a new iPod. His parents gave him $10 for his birthday to open his savings account. The equation y = 20x + 10 represents John’s savings account balance x months after he began saving.
Part (a),
The number of the months will be calculated as,
y = 20x + 10
300 = ( 20 x + 10 )
290 = 20x
x = 14¹/₂ months
Part(b),
The slope will be 40 for the saving of $40.
To know more about an equation of the line follow
https://brainly.com/question/18831322
#SPJ2
Related Questions
Find the measures of the numbered angles.
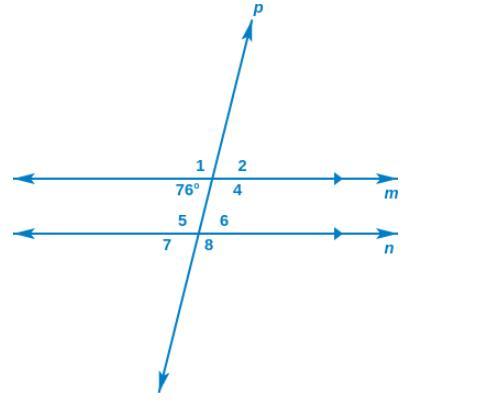
Answers
Answer: <1=104 degrees, <2=76 degrees, <4=104 degrees, <5=104 degrees, <6= 76 degrees, <7= 76 degrees, <8= 104 degrees
Step-by-step explanation:
<76 & < 2 are vertical angles, which means they are congruent. <1 & <2 are supplements, meaning when you add them up they equal 180 degrees (180-76=104 degrees). <1 & <4 are vertical angles. Using the Alternating Exterior Angles Theorem (AIA), <2 & <7 are congurent. Using the same theorem, <1 & < 8 are congruent. <7 & <5 are supplements, and so is <8 & <6.
What will be the value stored in the variable x after the execution of the following code snippet?
int a = 10;
int b = 20;
int c = 2;
int x = b / a /*c*/;
a) 1
b) 2
c) 4
d) The code has a syntax error
Answers
The value stored in the variable x after the execution of the following code snippet will be b) 2.
The right-click context menu option or a combination of hotkeys can be used to add code snippets, which are compact chunks of reusable code, to a code file. Although try-finally and if-else blocks, for example, are frequently used code blocks found in code snippets, you can also use them to add whole classes or methods.
Learn more about using the templates tool to create reusable emails. Applications and web pages use snippets. Snippets are made to be reusable and to add functionality, like connecting various parts of a program.
To learn more about code snippet: https://brainly.com/question/29845639
#SPJ4
Find the measure of the numbered angle

Answers
Answer:
115°
Step-by-step explanation:
1/2 (130 + 100) = 115°
What are the domain restrictions of q^2−7q−8 divided by q^2+3q−4 ?
o q≠1 and q≠−8
o q≠−1 and q≠8
o q≠−1 and q≠4
o q≠1 and q≠−4
Answers
The domain restrictions of the expression q²−7q−8/q²+3q−4 are q ≠ -4 and q ≠ 1. (option c)
The denominator of the expression is q²+3q−4. To determine the values that would make the denominator equal to zero, we can set it equal to zero and solve for q:
q² + 3q - 4 = 0
Now, we can factorize the quadratic equation:
(q + 4)(q - 1) = 0
To find the values of q, we set each factor equal to zero and solve for q:
q + 4 = 0 or q - 1 = 0
Solving these equations, we get:
q = -4 or q = 1
So, the values of q that would make the denominator equal to zero are q = -4 and q = 1. These are the values we need to exclude from the domain of the expression to avoid division by zero.
Therefore, the correct answer is option c) q ≠ 1 and q ≠ -4.
To know more about domain here
https://brainly.com/question/28599653
#SPJ4
Complete Question:
What are the domain restrictions of q²−7q−8/q²+3q−4?
a) q≠1 and q≠−8
b) q≠−1 and q≠4
c) q≠1 and q≠−4
d) q≠−1 and q≠8
Help please Math is annoying.

Answers
Answer:
1
Step-by-step explanation:
so you want to input the numbers into variables so for (p+q)^2 you input p as 4 and q as 8 (4+8)^2 and then you add 4+8 which is 12. Then you have to do 12 to the power of 2 which is 12x12 and the answer to that is 144. For the bottom you input p as 4 and then for -2q you have to input the 8, -2(8) and that equals to -16 so then it's 4-16 so it equals to -12. Then you have to do -12 divided by 12 which equals to 1.
In a study to estimate the proportion of residents in a certain city and its suburbs who favor the construction of a nuclear power plant, it is found that 74 of 100 urban residents favor the construction while only 70 of 125 suburban residents are in favor. Is there a significant difference between the proportions of urban and suburban residents who favor constructing nuclear plants
Answers
The p value for the difference is 0.005.
According to the statement
we have given that the 74 of 100 urban residents favor the construction while only 70 of 125 suburban residents are in favor.
And we have to find the difference between them in proportions.
So,
X1 = 74 represent the number of residents in a certain city and its suburbs who favor the construction of a nuclear power plant
X2 = 70 represent the number of people suburban residents are in favor
N1 = 100 sample 1 selected
N2 = 125 sample 2 selected
AND
P1 = 0.74 represent the proportion of residents in a certain city and its suburbs who favor the construction of a nuclear power plant
And P2 = 0.56 represent the proportion of suburban residents are in favor And z would represent the statistic (variable of interest)
Pv represent the value for the test (variable of interest)
Here we apply the Z test to find the difference then
Z = (0.74 - 0.56) / (0.64(1-0.64)(1/100+1/125) )^1/2
Now after solving
Z = 2.795.
Now The significance level provided is ,and we can calculate the p value for this test.
Since is a two tailed test the p value would be:
P = (z>2,795)
P = 0.005.
So, The p value for the difference is 0.005.
Learn more about Z Test here https://brainly.com/question/14453510
#SPJ4
Nancy and bill collect coins. Nancy has x coins. Bill has 9 coins fewer than four times the number of coins Nancy has. Write and simplify an expression for the total number of coins Nancy and bill have.
Answers
Answer:
3x-9
Step-by-step explanation:
4x-9 = bill
x = nancy
4x-9+x = total
i stG
go home
take a nap
highly recommend
quit math class
drop out of school
gn boo
Evaluate.0.2 power of 4 =
Answers
Answer:
0.0016
Step-by-step explanation:
The expression 0.2 by the power of 4 when evaluated has a value of 0.0016
How to evaluate the expressionFrom the question, we have the following parameters that can be used in our computation:
0.2 by the power of 4
Express as an equation
So, we have
0.2 by the power of 4 = 0.2⁴
When expanded, we have
0.2 by the power of 4 = 0.2 * 0.2 * 0.2 * 0.2
Evaluate the products
This gives
0.2 by the power of 4 = 0.0016
Hence, the solution is 0.0016
Read more about expression at
https://brainly.com/question/30492964
#SPJ6
5x + 2y = 8 x + y = 4 if you want to solve the system of equations by addition which of the following could you do
Answers
Answer: x= 0, y = 4
Step-by-step explanation:
5x+2y=8
X+y=4 -> y=4-x
5x + 2(4-x)=8 -> 5x + 8-2x=8 -> 3x=0 -> x=0
y=4-x=4-0=4
let a and b be integers. prove that if ab = 4, then (a – b)3 – 9(a – b) = 0.
Answers
Let \(\(a\)\) and \(\(b\)\) be integers such that \(\(ab = 4\)\). We want to prove that \(\((a - b)^3 - 9(a - b) = 0\).\)
Starting with the left side of the equation, we have:
\(\((a - b)^3 - 9(a - b)\)\)
Using the identity \(\((x - y)^3 = x^3 - 3x^2y + 3xy^2 - y^3\)\), we can expand the cube of the binomial \((a - b)\):
\(\(a^3 - 3a^2b + 3ab^2 - b^3 - 9(a - b)\)\)
Rearranging the terms, we have:
\(\(a^3 - b^3 - 3a^2b + 3ab^2 - 9a + 9b\)\)
Since \(\(ab = 4\)\), we can substitute \(\(4\)\) for \(\(ab\)\) in the equation:
\(\(a^3 - b^3 - 3a^2(4) + 3a(4^2) - 9a + 9b\)\)
Simplifying further, we get:
\(\(a^3 - b^3 - 12a^2 + 48a - 9a + 9b\)\)
Now, notice that \(\(a^3 - b^3\)\) can be factored as \(\((a - b)(a^2 + ab + b^2)\):\)
\(\((a - b)(a^2 + ab + b^2) - 12a^2 + 48a - 9a + 9b\)\)
Since \(\(ab = 4\)\), we can substitute \(\(4\)\) for \(\(ab\)\) in the equation:
\(\((a - b)(a^2 + 4 + b^2) - 12a^2 + 48a - 9a + 9b\)\)
Simplifying further, we get:
\(\((a - b)(a^2 + 4 + b^2) - 12a^2 + 39a + 9b\)\)
Now, we can observe that \(\(a^2 + 4 + b^2\)\) is always greater than or equal to \(\(0\)\) since it involves the sum of squares, which is non-negative.
Therefore, \(\((a - b)(a^2 + 4 + b^2) - 12a^2 + 39a + 9b\)\) will be equal to \(\(0\)\) if and only if \(\(a - b = 0\)\) since the expression \(\((a - b)(a^2 + 4 + b^2)\)\) will be equal to \(\(0\)\) only when \(\(a - b = 0\).\)
Hence, we have proved that if \(\(ab = 4\)\), then \(\((a - b)^3 - 9(a - b) = 0\).\)
To know more about satisfies visit-
brainly.com/question/16993710
#SPJ11
which best explains whether a triangle with side lengths 5cm 13cm and 12 cm is a right triangle
Answers
Answer: the awnser is 0 jk its not
Step-by-step explanation:
i just want point repete dkmkmkrfnjrjnnfrfr
Answer:
Yes, it can make a right triangle.
Step-by-step explanation:
We can use the Pythagorean Theorem to determine if the sides make a right triangle.
\(a^2+b^2=c^2\)
We are given the side lengths: 5cm, 13cm, and 12 cm.
13cm is the longest, so it would be 'c'.
5cm and 12cm will be 'a' and 'b'.
Let 5 be 'a', 12 be 'b', and 13 be 'c':
\(5^2+12^2=13^2\\\\\text{Solve the Exponents:}\\ \rightarrow 5^2=25\\\rightarrow 12^2=144\\\rightarrow 13^2=169\\\\25+144=169\\\boxed{169=169}\)
5cm, 13cm, and 12 cm would make a right triangle. It satisfies the Pythagorean Theorem.
PLEASE HELP!! I'LL GIVE YOU BRAINLIEST !!

Answers
Answer:
1 ) a 2) b 3) d 4) b 5) a 6) c
Step-by-step explanation:
Find the coordinates of P so that P partitions segment AB in the part-to-whole ratio of 1 to 3 with A(6, -10) and B(9, -1).
Answers
Answer:
Step-by-step explanation:
Use the formulas that allow us to find the point that divides the segment into a ratio which is
\(x=\frac{bx_1+ax_2}{a+b}\) and \(y=\frac{by_1+ay_2}{a+b}\) where a is 1 (comes from the ratio) and b is 3 (comes from the ratio as well). Filling in:
\(x=\frac{3(9)+1(6)}{1+3}=\frac{27+6}{4}=\frac{33}{4}\) and then y:
\(y=\frac{3(-1)+1(-10)}{1+3}=\frac{-3-10}{4}=-\frac{13}{4}\) so the coordinates in question are
\((\frac{33}{4},-\frac{13}{4})\)
Answer:
Step-by-step explanation:
the answer would be (7,-7)
2) Gas mileage is the number of miles you can drive on a a gallon of gasoline.
A test of a new car results in 510 miles on 10 gallons of gas. How far could
you drive on 55 gallons of gas? What is the car's gas mileage?
Help me please!!
This is my last question ..
Answers
Answer:
You could drive 2805 miles on 55 gallons of gas
The car's gas mileage is 51 miles per gallon
Step-by-step explanation:
First, find the gas mileage by dividing the given number of miles by the number of gallons:
510/10
= 51
The car's gas mileage is 51 miles.
Find how far you can drive on 55 gallons of gas by multiplying 51 by 55
51(55)
= 2805
So, you can drive 2805 miles.
you get in a elevator and go down 8 floors. You exit on the 16th floor. What floor you on the elevator
Answers
Answer:
24th floor
Step-by-step explanation:
To get the number of the floor you were originally on, you add the number of floors you went down to the current floor you are on so 16 + 8 = 24
Answer:
24
Step-by-step explanation:
x-8=16
16+8=24
What is the mode of the data set: 17,13,18,20,17,15,12
Answers
Answer:
17
Step-by-step explanation:
17 is the most frequent number showing in the set.
Step-by-step explanation:
Mode = Most frequently occurred data
Mode = 17 (as 17 occurred 2 times in the given set of data)
1. If f(x) = x + 3 and g(x) = x² + 2x - 3, find [gxf](x).
.](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/QqdohEyZ5AH43SKbVB6N3UsErmApcVLF.png)
Answers
The answer is g(f(x)) =(x+6)(x+2)
From the question, we have
f(x) = x + 3 and g(x) = x² + 2x - 3
g(f(x)) = g(x + 3)
=(x + 3)² + 2(x + 3) - 3
=x² + 9+6x+2x+6-3
=x² + 8x+12
=x² + 6x+2x+12
=(x+6)(x+2)
The answer is g(f(x)) =(x+6)(x+2)
Multiplication:
Mathematicians use multiplication to calculate the product of two or more numbers. It is a fundamental operation in mathematics that is frequently utilized in everyday life. When we need to combine groups of similar sizes, we utilize multiplication. The fundamental concept of repeatedly adding the same number is represented by the process of multiplication. The results of multiplying two or more numbers are known as the product of those numbers, and the factors that are multiplied are referred to as the factors. Repeated addition of the same number is made easier by multiplying the numbers.
To learn more about multiplication visit: https://brainly.com/question/5992872
#SPJ1
g how many times would you expect a person selected at random to have to take the test until (s)he passes it? (if necessary, round your answer to 2 decimal places.)
Answers
The probability that a person selected at random to have the test until (s)he passes the test is, 0.03125
Given, a test occurred 5 times in a class.
we have to find that how many times a person selected at random to have the test until (s)he passes it.
the probability of getting pass in the exam be, 1/2
and similarly the probability of getting fail in the exam also be, 1/2
so, the probability that a person selected at random to have the test until (s)he passes the test is,
(1/2)^5
= 1/32
= 0.03125
Hence, the probability that a person selected at random to have the test until (s)he passes the test is, 0.03125
Learn more about Probability here https://brainly.com/question/27745646
#SPJ4
What is the yield to maturity (YTM) on a simple loan for $1,500 that requires a repayment of $7,500 in five years' time? The yield to maturity is ?
Answers
The yield to maturity on a simple loan for $1,500 that requires a repayment of $7,500 in five years' time is 37.14%.
Yield to maturity (YTM) is the total return anticipated on a bond or other fixed-interest security if the security is held until it matures. Yield to maturity is considered a long-term bond yield, but is expressed as an annual rate. In this problem, the present value (PV) of the simple loan is $1,500, the future value (FV) is $7,500, the time to maturity is five years, and the interest rate is the yield to maturity (YTM).
Now we will calculate the yield to maturity (YTM) using the formula for the future value of a lump sum:
FV = PV(1 + YTM)n,
where,
FV is the future value,
PV is the present value,
YTM is the yield to maturity, and
n is the number of periods.
Plugging in the given values, we get:
$7,500 = $1,500(1 + YTM)5
Simplifying this equation, we get:
5 = (1 + YTM)5/1,500
Multiplying both sides by 1,500 and taking the fifth root, we get:
1 + YTM = (5/1,500)1/5
Adding -1 to both sides, we get:
YTM = (5/1,500)1/5 - 1
Calculating this value, we get:
YTM = 0.3714 or 37.14%
Therefore, the yield to maturity on a simple loan for $1,500 that requires a repayment of $7,500 in five years' time is 37.14%.
To know more about loan refer here:
https://brainly.com/question/31950305
#SPJ11
What is function and not function?
Answers
Answer: A function is a relation between domain and range such that each value in the domain corresponds to only one value in the range. Relations that are not functions violate this definition. They feature at least one value in the domain that corresponds to two or more values in the range.
Step-by-step explanation:
Can i please get some help :)

Answers
1,750
Solve the equation:
64 x 216^x =54^x
Answers
Answer:
x=1/256
Step-by-step explanation:
hope it helps you
In exercise 11-14 find the value of x for each one thank you whoever gets all of it right gets brainliest

Answers
The missing angles of the given quadrilaterals are 64°, 68°, 89° and 99°
What are quadrilaterals?A quadrilateral is a four-sided polygon, having four edges and four corners.
Given are quadrilaterals, we need to find the missing angles in them,
So, to find the missing angles, we will use the concept of sum of interior angles of a quadrilateral,
We know that, the sum of interior angles of a quadrilateral, is 360°
a) ∠ W + ∠ X + ∠ Y + ∠ Z = 360°
x + 100° + 130° + 66° = 360°
x = 360° - 296°
x = 64°
b) ∠ G + ∠ H + ∠ J + ∠ K = 360°
x + 103° + 133° + 58° = 360°
x = 360° - 294°
x = 68°
c) ∠ K + ∠ L + ∠ M + ∠ N = 360°
88° + 154° + x + 29° = 360°
x = 360° - 271°
x = 89°
d) ∠ A + ∠ B + ∠ C + ∠ D = 360°
x + 92° + 68° + 101° = 360°
x = 360° - 261°
x = 99°
Hence, the missing angles of the given quadrilaterals are 64°, 68°, 89° and 99°
Learn more about quadrilaterals, click;
https://brainly.com/question/29934291
#SPJ1
Fractions less then 1/2
Answers
Answer:
Step-by-step explanation:
16 fractions less than one half
1/9, 2/9, 3/9, 4/9, 1/8, 2/8, 3/8, 1/7, 2/7, 3/7, 1/6, 2/6, 1/5, 2/5, 1/4, 1/3
Answer:
1/3, 1/4, 1/5, 1/6
which number is the smallest
a. 1.28x10-^4
b.2.85x10-^6
c.3.24x10-^5
d.5.48x10-^8
Answers
Answer: I think so A because it being multiple by 10 and u can get 6
Step-by-step explanation:
Answer:
A
Step-by-step explanation:
because it has the smallest power
Tekan-Tekan Sdn. Bhd. has order for 200 Model AS-120 calculator for delivery on day 200. The calculator consists of three parts. Components 2 and 3 form subassembly 1 . Sub-assembly 1 and component 4 form the final assembly. Following are the work centers and times of each operation. Table Q3(a) shows routine file of the operation. Assuming: - Only one machine is assigned to each operation - The factory works on 8-hour shift, 5 days a week - All parts move in one lot of 200. (a) Illustrate the backward schedule based on the information given above. (12 marks) (b) Identify when component 3 must be started to meet the delivery date. (2 marks)
Answers
Component 3 must be started on day 197 to meet the delivery date of day 200.
To illustrate the backward schedule, we need to start from the delivery date (day 200) and work our way backward, taking into account the lead times and dependencies of each operation.
(a) Backward schedule:
Operation | Work Center | Time (hours) | Start Day
--------------------------------------------------------
Final Assembly | Work Center 1 | 1 | 200
Sub-assembly 1 | Work Center 2 | 2 | 199
Component 4 | Work Center 3 | 3 | 197
Component 2 | Work Center 4 | 4 | 196
Component 3 | Work Center 5 | 3 | ????
(b) To identify when component 3 must be started to meet the delivery date, we need to consider its dependencies and lead times.
From the backward schedule, we see that component 3 is required for sub-assembly 1, which is scheduled to start on day 199. The time required for sub-assembly 1 is 2 hours, which means it should be completed by the end of day 199.
Since component 3 is needed for sub-assembly 1, we can conclude that component 3 must be started at least 2 hours before the start of sub-assembly 1. Therefore, component 3 should be started on day 199 - 2 = 197 to ensure it is completed and ready for sub-assembly 1.
Hence, component 3 must be started on day 197 to meet the delivery date of day 200.
Learn more about Scheduling here:
brainly.com/question/30012511
#SPJ4
Mona has a bag containing 4 red marbles, 12 greens marbles, and 8 black marbles. Without looking, she pulls out one marble from the bag and places it in an empty jar. She then pulls a second marble from the bag and places it in the jar. What is the probability that she will have 2 red marbles in the jar?

Answers
Answer: C (4/24*3/23)
Step-by-step explanation:
4 red
12 green
8 black
24 total
pulling red on the first pull:
4/24
pulling red on the second pull:
3/23
so C
Let P(n) be the equation: 11⋅2+12⋅3+⋅⋅⋅+1n⋅(n+1)=nn+1 for all the natural numbers n≥1.
A mathematical induction proof consists of two steps: the basis step and the inductive step. Answer the following questions: Show the equation is true in the basis step. What is the equation of the inductive hypothesis (IH)? You don't need to show the equation is true. What is the equation we need to show in the inductive step?
Answers
In the basis step of the mathematical induction proof for P(n), we show that the equation is true for n = 1. The equation of the inductive hypothesis (IH) is P(k), where k is an arbitrary natural number. In the inductive step, we need to show that if P(k) is true, then P(k+1) is also true.
In the basis step, we substitute n = 1 into the equation 11⋅2+12⋅3+⋅⋅⋅+1n⋅(n+1)=nn+1. This gives us the equation 1⋅2 = 1+1, which is true.
The inductive hypothesis (IH) is denoted as P(k), where k is an arbitrary natural number. We assume that P(k) is true, meaning that 11⋅2+12⋅3+⋅⋅⋅+1k⋅(k+1)=kk+1 holds.
In the inductive step, we need to show that if P(k) is true, then P(k+1) is also true. This involves substituting n = k+1 into the equation 11⋅2+12⋅3+⋅⋅⋅+1n⋅(n+1)=nn+1 and demonstrating that the equation holds for this value. The specific equation we need to show in the inductive step is 11⋅2+12⋅3+⋅⋅⋅+1(k+1)⋅((k+1)+1)=(k+1)(k+1+1).
Learn more about inductive hypothesis here: brainly.com/question/31703254
#SPJ11
In the basis step, we need to show that the equation P(1) is true. The equation of the inductive hypothesis (IH) is P(k), where k is any natural number greater than or equal to 1. In the inductive step, we need to show that if P(k) is true, then P(k+1) is also true.
To prove the equation P(n): 11⋅2 + 12⋅3 + ... + 1n⋅(n+1) = n(n+1) using mathematical induction, we follow the two-step process.
1. Basis Step:
We start by showing that the equation is true for the base case, which is n = 1:
P(1): 11⋅2 = 1(1+1)
Simplifying, we get: 2 = 2, which is true.
2. Inductive Step:
Assuming that the equation is true for some arbitrary value k, the inductive hypothesis (IH) is:
P(k): 11⋅2 + 12⋅3 + ... + 1k⋅(k+1) = k(k+1)
In the inductive step, we need to show that if P(k) is true, then P(k+1) is also true:
P(k+1): 11⋅2 + 12⋅3 + ... + 1k⋅(k+1) + 1(k+1)⋅((k+1)+1) = (k+1)((k+1)+1)
By adding the (k+1)th term to the sum on the left side and simplifying the right side, we can demonstrate that P(k+1) is true.
Learn more about equation here: brainly.com/question/30130739
#SPJ11
1. Fill in the chart
Words
Expression
The Value of the Expression
a. 50 times the sum of 64 and 36
50 x 64 + 36 )
5000
b. Divide the difference between
1,200 and 700 by 5
(1,200 - 700): 5
100
C. The sum of 3 fifteens and 17
fifteens
45 + 255
d. 15 times the sum of 14 and 6
e.
10 x (250 +45)
f.
(560 + 440) x 14
Answers
Answer:
See answers in bold
Step-by-step explanation:
Words Expression
The Value of the Expression
a. 50 times the sum of 64 and 36 ... 50 x (64+36) = 50x (100) = 5000
50 x 64 + 36 )
5000
b. Divide the difference between 1,200 and 700 by 5 ...(1200-700) / 5 = 500/5 = 100
(1,200 - 700): 5
100
C. The sum of 3 fifteens and 17 fifteens ... \(\frac{3}{15}\) + \(\frac{17}{15}\) = \(\frac{20}{15}\) = \(\frac{4}{3}\)
45 + 255
d. 15 times the sum of 14 and 6 ... 15 x (14 + 6) = 15 (20) = 300
e.
10 x (250 +45) ...10 times the sum of 250 and 45
f.
(560 + 440) x 14... 14 times the sum of 560 and 440
Hope this helps
find the volume common to two spheres, each with radius r, if the distance between their centers is r/2.
Answers
The volume common to two spheres, each with radius r, if the distance between their centres is r/2 is V = (11/12)×π×r³.
The attached diagram shows 2 circumferences with radius r and separated centres by r/2.
Let´s call circumferences 1 and 2; by symmetry, rotating area A will produce a volume V₁ identical to a V₂, Obtained by rotating area B ( both around the x-axis), then the whole volume V will be:
V = 2× V₁
V₁ = ∫π×y²×dx (1)
Now
( x - r/2)² + y² = r² the equation of circumference 1
y² = r² - ( x - r/2)²
Plugging this value in equation (1)
V₁ = ∫π×[ r² - ( x - r/2)²]×dx with integrations limits 0 ≤ x ≤ r/2
V₁ = π×∫ ( r² - x² + (r/2)² - r×x )×dx
V₁ = π× [ r²×x - x³/3 + (r/2)²×x - (1/2) × r × x²] evaluate between 0 and r/2
V₁ = π× [(5/4)×r²×x - x³/3 - (1/2) × r × x²]
V₁ = π× [(5/4)×r² × ( r/2 - 0 ) - (1/3)×(r/2)³ - (1/2) × r × (r/2)²]
V₁ = π× [ (5/8)×r³ - r³/24 - r³/8]
V₁ = π× (11/24)×r³
Then
V = 2× V₁
V = 2×π×11/24)×r³
V = (11/12)×π×r³
To know more about volume, here
https://brainly.com/question/22907480
#SPJ4
