Juan needs to rent a car for his road trip to Savannah, GA. Juan asks his friends if he knows how much the car rental costs. Nadia says she paid $50 for a two-day car rental. Johanna says she paid $75 for a three-day rental, and Kristine paid $100 for a four-day rental.
Juan made the table below to help him visualize how much his car rental will cost.
Answers
Answer:
ok whats the question?
Step-by-step explanation:
i only see the explanation
Related Questions
Almonds are sold in 8-ounce and 20-ounce packages. What is the least number of ounces you can buy of each package to have equal amounts of each package size?
The least number of ounces you can buy of each package to have equal amounts of each package size is ounces
Answers
Answer:
40
Step-by-step explanation:
\(8=2^3 \\ \\ 20=2^2 \times 5 \\ \\ \lcm(8,20)=2^3 \times 5=40\)
Prove the Converse of the Pythagorean Theorem
In this activity, you will prove and apply the converse of the Pythagorean theorem. Recall that the
converse states that if the square of the length of the longest side of a triangle is equal to the sum of
the squares of the other two sides, then the triangle is a right triangle.
Open the GeoGebra activity to complete each step below. For help, watch these short videos about
using GeoGebra to measure and create points, lines, and anglese.
Question 1
Part A
Draw AABC with vertices at A(1,6), B(1, 1) and C(5,1). In this triangle, AB²+ BC² = AC².
Next, use the GeoGebra tools to draw ADEF such that AB = DE, m/E
Paste a picture of your drawing in the answer box.
= 90°, and EF
BC.
B I U X² X2 15px
AVA
E E g = = 三 四 V 田
=
Answers
The based on this example, we can see that the converse of the Pythagorean theorem does not hold for this particular triangle.
To prove the converse of the Pythagorean theorem, we need to show that if the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.
In the given triangle AABC, with vertices at A(1,6), B(1,1), and C(5,1), we can calculate the lengths of the sides using the distance formula or Pythagorean theorem.
AB = sqrt((1-1)^2 + (6-1)^2) = sqrt(25) = 5
BC = sqrt((5-1)^2 + (1-1)^2) = sqrt(16) = 4
AC = sqrt((5-1)^2 + (6-1)^2) = sqrt(40) = 2sqrt(10)
Now, let's check if AB^2 + BC^2 = AC^2:
AB^2 + BC^2 = 5^2 + 4^2 = 25 + 16 = 41
AC^2 = (2sqrt(10))^2 = 4(10) = 40
Since AB^2 + BC^2 is not equal to AC^2, the given triangle AABC does not satisfy the condition for the converse of the Pythagorean theorem.
For more such questions on Pythagorean theorem:
https://brainly.com/question/28981380
#SPJ8
derrick is preparing to submit his taxes. over the year, he kept track of certain deductions he is able to claim (all rounded to the nearest dollar). these values are given below. 65,144,97,144,103,98,101,127,58,151 derrick figures that he will receive the following amounts: $25 for each deduction that is under $130 and $45 for each deduction that is $130 or more. use the ti-83 or 84 to draw a histogram for these values using 4 classes. using that histogram, determine how much total derick will receive from all of his deductions.
Answers
Derrick will receive total of $340 from all of his deductions
To create a histogram for these values using four classes, we must first determine the class width, which is determined as the data range divided by the number of classes. The data range is 151 - 58 = 93, which is the difference between the biggest and smallest numbers. The breadth of the class is 93/4 = 23.25. We'll round it up to 24 because we can't have a fractional class width.
Then, for each of the four classes, we'll start with the smallest number (58) and add the class width (24) again until we reach the maximum value (151). The lowest class boundaries for the four classes are as follows:
Class 1: 58
Class 2: 82
Class 3: 106
Class 4: 130
We'll determine the upper class limit for each lower class limit by adding the class width (24) - 1. The upper class restrictions are as follows:
Class 1: 81
Class 2: 105
Class 3: 129
Class 4: 153
Finally, we'll tally the amount of deductions made in each class and utilise that data to create the histogram. Each class has the following number of deductions:
Class 1: 1 (58)
Class 2: 3 (97, 98, 101)
Class 3: 3 (103, 127, 144)
Class 4: 3 (144, 151, 65)
We can compute the total amount Derrick will earn from all of his deductions now that we know the number of deductions in each class. He will earn $25 for each deduction of less than $130, and $45 for each deduction of $130 or more.
Derrick will receive the following total from all of his deductions:
$25 * 1 (for the single deduction of less than $130) + $45 * 7 (for the seven deductions of $130 or over) = $25 + $315 = $340
For more such questions on Histogram, click on:
https://brainly.com/question/25983327
#SPJ4
The equation 4(x-2)=100 is a true equation for a particular value of x.
Without solving, explain why 2(x-2)=50 is also true for the same value of
X. *
need this asap!!
Answers
Answer:
Yes because x=27
Step-by-step explanation:
4(x-27)=100
4(25)=100
100=100
and
2(27-2)=50
2(25)=50
50=50
A particle moves in the xy plane so that at any time
,
x=3sint
and
.y=t-4cost+1
What is the vertical component of the particle's location when it's horizontal component is 2?
Responses
y = -1.05
y = -1.05
y = -2.25
y = -2.25
y = -1.25
y = -1.25
y = 0.73
Answers
The vertical component of the particle's location, when its horizontal component is 2, is:
y = -1.25
How to solveTo find the vertical component of the particle's location when its horizontal component is 2, we need to first find the value of t when x = 2.
Given the equation:
x = 3sin(t)
Substitute x with 2:
2 = 3sin(t)
Now, isolate t by dividing both sides by 3:
sin(t) = 2/3
Take the inverse sine (arcsin) of both sides:
t = arcsin(2/3)
Now, plug the value of t back into the y equation:
y = t - 4cos(t) + 1
y = arcsin(2/3) - 4cos(arcsin(2/3)) + 1
Using a calculator to find the approximate value of y, we get:
y ≈ -1.25
Therefore, the vertical component of the particle's location when its horizontal component is 2 is:
y = -1.25
Read more about vertical components here:
https://brainly.com/question/25854506
#SPJ1
please hurry and I will give you brainlest if you are correct Graph the Solution to this inequality on the number line

Answers
Answer:
x < 3 1/4
See picture below.
Step-by-step explanation:
1/2 x - 3 < -1 3/8
1/2 x < -11/8 + 24/8
1/2 x < 13/8
x < 13/4
x < 3 1/4

suppose section 1 has 30 students and section 2 has 20. find the sd of the scores of all the students in the class
Answers
The standard deviation of the scores of all the students in the class to be:
σ = √[(Σ(x - 80)2) / 50] = 11.18
The standard deviation of the scores of all the students in the class is calculated using the formula
σ = √[(Σ(x - μ)2) / N]
where μ is the mean of the scores and N is the total number of students in the class.
In this case, the total number of students in the class is 50 (30 from section 1 and 20 from section 2). Let's assume that the mean of the scores for all students is 80.
Therefore, the standard deviation of the scores of all the students in the class is calculated as follows:
σ = √[(Σ(x - 80)2) / 50]
In this equation, Σ(x - 80)2 is the sum of the squared differences between each student's score and the mean. We can calculate this sum by first finding the squared difference for each student and then adding them up.
For example, if the scores of the 30 students in section 1 are 86, 95, 78, etc., the squared differences will be (86 - 80)2 = 36, (95 - 80)2 = 225, (78 - 80)2 = 4, and so on. Adding all these squared differences will give us the sum of the squared differences for all the students in the class.
Finally, substituting this sum and the value of N (50) in the formula, we get the standard deviation of the scores of all the students in the class to be:
σ = √[(Σ(x - 80)2) / 50] = 11.18
Learn more about standard deviation here:
https://brainly.com/question/23907081
#SPJ4
How many liters each of a 30% acid solution and a 50 % acid solution must be used to produce 70 liters of a 40 % acid solution? (Round to two decimal places if
necessary.)
Answers
Answer:
30%: 35 liters
50%: 35 liters
Step-by-step explanation:
The desired concentration is halfway between the concentrations of available solutions, so the mixture will be equal amounts of each.
35 liters of 30% acid and 35 liters of 50% acid must be used
_____
If you want to write an equation, it usually works well to let the variable represent the amount of the most concentrated constituent: 50% acid. Then the amount of acid in the final mix is ...
0.50x +0.30(70 -x) = 0.40(70)
0.20x +21 = 28 . . . . simplify
0.20x = 7 . . . . . . . . . subtract 21; next, divide by 0.20
x = 35 . . . . . . amount of 50% solution (liters)
70-x = 35 . . . amount of 30% solution (liters)
HELPPPPP!!!!!!!!!!!!!!

Answers
Answer:
B.
Step-by-step explanation:
-2/3
from the y-intersect (0,0), you went up 2 units(positive) and left 3 times (negative) to get the other points so negative and positive are negative.
What is the volume of the composite figure?
A complex figure comprised of 2 rectangular prisms. Prism A has a length of 7 inches, a width of 3 inches, and a height of 2 inches. Prism B has a length of 3 inches, width of 3 inches, and height of 7 inches.
69 in.3
105 in.3
276 in.3
4,536 in.3
Answers
Therefore, the volume of the composite figure is 105 cubic inches.
What is volume?In physics and mathematics, volume refers to the amount of space occupied by a three-dimensional object or region. It is a measure of the size of an object in three dimensions, and is typically expressed in cubic units, such as cubic meters, cubic feet, or cubic centimeters. The volume of an object can be calculated using a formula that is specific to the shape of the object. For example, the volume of a cube can be calculated by multiplying the length, width, and height of the cube, while the volume of a sphere can be calculated using the formula 4/3 x π x r^3, where r is the radius of the sphere. The concept of volume is important in many fields, including architecture, engineering, and science, as it is used to calculate the amount of space that an object or substance occupies, and to determine quantities such as mass and density.
Here,
To find the volume of the composite figure, we need to find the volume of each rectangular prism and add them together.
The volume of a rectangular prism is given by the formula V = l*w*h, where l is the length, w is the width, and h is the height.
For Prism A, V = (7)(3)(2) = 42 cubic inches.
For Prism B, V = (3)(3)(7) = 63 cubic inches.
The total volume of the composite figure is the sum of the volumes of the two prisms:
V_total = V_A + V_B
= 42 + 63
= 105 cubic inches
To know more about volume,
https://brainly.com/question/12237641
#SPJ1
Two systems of linear equations in two variables, x and y, are given.
System P:
(3x-10y=8
7x+2y=6
The two systems have the same solution..
What are the values of b and c?
b=
System T:
bx - 10 y + 10 y = 38
cx + 10 y = 30
=
C =

Answers
Answer:
Step-by-step explanation:
PleAse help what do I time I’m having a hard time?

Answers
Answer:
tan A = 6/5
Step-by-step explanation:
They give you cscA. This gives you info to also know sinA. csc and sin are reciprocals (just flip csc over to find sin).
Also, sin is OPP/HYP.
This means that
sin A is 6/root61.
6 is the side opposite from A. And root61 is the hypotenuse.
We can use pythagorean thm to find the other leg of the triangle.
see image.
tan A = OPP/ADJ
tan A = 6/5

PLZZ SOMEONE GIVE ME THE EQUATION!! You have $20 to buy snacks for yourself and 4 friends. If you buy a bag of chips for each person, and still have $13.75 left, how much did you spend on each bag of chips?

Answers
Answer:
1.56
Step-by-step explanation:
Answer:
1.25
Step-by-step explanation:
20-13.75 = 6.25
6.25 / 5 = 1.25
We want to factor the following expression: x^3 - 25 which pattern can we use to factor the expression? U and V are either constant integers or single variable expression.
Answers
The pattern that is used to factor the expression x³ - 25 is given as follows:
B. (U - V)(U + V).
What is the subtraction of perfect squares?The subtraction of perfect squares is a notable product that gives the simplification of an expression containing the subtraction of perfect squares, as the multiplication of the square roots of the two terms subtracted by the square of the two terms subtracted, as follows.
a² - b² = (a - b)(a + b).
In the context of this problem, the expression is presented as follows:
x³ - 25.
The square root of x³ is obtained as follows:
sqrt(x³) = (x³)^(0.5) = x^(3 x 0.5) = x^1.5 = \(\sqrt{x^3}\)
The square root of 25 is obtained as follows:
5.
Because 5² = 25.
Then, applying the subtraction of perfect squares notable product, the factored expression is given as follows:
\(x^3 - 25 = (\sqrt{x^3} - 5)(\sqrt{x^3} + 5)\)
Which is the pattern given by option B.
Missing InformationThe complete problem is given by the image shown at the end of the answer.
A similar problem, also featuring subtraction of perfect squares, is presented at https://brainly.com/question/28792378
#SPJ1

5(y+2/5)=-13
need help asap rocky
Answers
Answer:
y=-3
Step-by-step explanation:
first distribute then solve for y
5y+2=-13
-2 on both sides
5y=-15
divide by five on each side
y=-3
Answer:
y = -3
Step-by-step explanation:
5(-3 + 2/5) = -13
2/5 = 0.4
5(-3 + 0.4) = -13
5(-2.6) = -13
Do the multiplication on a calculator
5 x -2.6 = -13
-13 = -13
look at the figure. i’ll give you brainlest!!!

Answers
Answer:
u already got it cos x = 8f
Step-by-step explanation:
A quarterback completes 44% of his passes. Show all work.
a. Construct a probability distribution table (out to n = 6) for the number of passes attempted before the quarterback has a completion?
b. What is the probability that the quarterback throws 3 incomplete passes before he has a completion?
c. How many passes can the quarterback expect to throw before he completes a pass?
d. Determine the probability that it takes more than 5 attempts before he completes a pass.
e. If he throws 8 passes on the opening drive, what is the probability that he made at least half of them?
Answers
a.The probability distribution table for the first six attempts is shown below:
X P(X=k)
1 0.44
2 0.56 ×0.44
3 0.56²×0.44
4 0.56³ × 0.44
5 0.56⁴ ×0.44
6 0.56⁵×0.44
b. the probability is 0.1399.
c. the quarterback can expect to throw about 2.27 passes before completing one.
d. the probability is 0.1865.
e. the probability is 0.7349.
what is probability?The possibility or chance of an event occurring is measured by probability. The expression is given as a number between 0 and 1, with 0 denoting impossibility and 1 denoting certainty. Compared to occurrences with a probability closer to 0, those with a probability closer to 1 are more likely to occur.
a. To construct a probability distribution table for the number of passes attempted before the quarterback has a completion, we can use the geometric probability distribution, which is given by:
P(X=k) = \((1-p)^{k-1}\)×p
where X is the number of attempts before the completion, p is the probability of completion on each attempt, and k is the number of attempts.
The probability distribution table for the first six attempts is shown below:
X P(X=k)
1 0.44
2 0.56 ×0.44
3 0.56²×0.44
4 0.56³ × 0.44
5 0.56⁴ ×0.44
6 0.56⁵×0.44
b. The probability that the quarterback throws 3 incomplete passes before he has a completion is given by:
P(X=3) = (1-0.44)³⁻¹× 0.44 × (1-0.44)⁰
= 0.56²×0.44
= 0.1399
Therefore, the probability is 0.1399.
c. The expected number of passes that the quarterback can throw before he completes a pass is given by the formula:
E(X) = 1/p
where p is the probability of completion on each attempt.
In this case, p = 0.44, so the expected number of passes is:
E(X) = 1/0.44
= 2.27
Therefore, the quarterback can expect to throw about 2.27 passes before completing one.
d. The probability that it takes more than 5 attempts before the quarterback completes a pass is given by:
P(X > 5) = 1 - P(X <= 5)
= 1 - [P(X=1) + P(X=2) + P(X=3) + P(X=4) + P(X=5)]
= 1 - [0.44 + (0.56 × 0.44) + (0.56² ×0.44) + (0.56³ × 0.44) + (0.56⁴×0.44)]
= 0.1865
Therefore, the probability is 0.1865.
e. If the quarterback throws 8 passes on the opening drive, the probability that he completes at least half of them is given by the binomial probability distribution, which is given by:
P(X ≥ 4) = 1 - P(X < 4)
where X is the number of completed passes and the probability of completion on each attempt is p = 0.44.
Using the binomial probability distribution table or calculator, we can find:
P(X≥4) = 1 - [P(X=0) + P(X=1) + P(X=2) + P(X=3)]
= 1 - [0.56⁸ + (8× 0.56⁷×0.44) + (28 × 0.56⁶ × 0.44²) + (56× 0.56⁵×0.44³)]
= 0.7349
Therefore, the probability is 0.7349.
To know more about distribution, visit:
https://brainly.com/question/31197941
#SPJ1
A rectangle is h units high. It's length 3 units more than it's height. What is the perimeter?
Answers
The perimeter of the rectangle is 4h + 6
What is an algebraic expression?An algebraic expression can be defined as an expression that is composed of terms, variables, coefficients, constants and factors.
These expressions are also made up of arithmetic operations, such as;
SubtractionAdditionMultiplicationDivisionBracketParenthesesThe formula for calculating the perimeter of a rectangle is expressed as;
Perimeter = 2( l + h)
Where;
l is the lengthh is the height of the rectanglel = 3 + h
Substitute the values
Perimeter = 2( 3 + h+ h)
expand the bracket
Perimeter = 2(3 + 2h)
Perimeter = 4h + 6
Hence, the expression is 4h + 6
Learn more about rectangles here:
https://brainly.com/question/25292087
#SPJ1
Find the surface area of the pyramid.
64in^2
56in^2
88in^2
118in^2

Answers
Answer:
To find the surface area of this pyramid, we must find the area of one triangle flap which we then multiply by 4 because there are 4 of those equal triangle flaps surrounding the base(square). Once we find the area of those triangles, we then find the base(square)'s area. Next, we add all those areas together to get the result of the surface area.
Formula for area of triangle;
A = BH x 1/2
Where 'B' represents the base, 'H' represents the height, and 1/2 is just dividing the product of those two lengths by 2.
Plug in what you know, given that the base of one triangle is 4, and the height is 6.
A = 4(6) x 1/2
A = 24 x 1/2
A = 24/2
A = 12, the area of one triangle is 12 inches.
Now, we find the area of all the triangles by multiplying the area of one triangle by 4.
12 = Area of triangle
4 triangles in total, so:
12(4)
= 48 inches is the area of all the triangles.
Now we find the area of the base(square) using the formula;
(vol of square formula)
A = \(s^{2}\)
Where 's' represents one side of the square which is being squared.
or
A = l · w
Where 'l' represents the length and 'w' represents the width.
Plug in what you know, given that one side of the square is 4 inches (as well as the length and width).
(I'll be using the formula \(s^{2}\))
A = \(s^{2}\)
A = 4^2 ← (The symbol ' ^ ' means raised to the power of.)
A = 16, the area of the base(square) is 16 inches.
Now we add both areas together:-
48 + 16
= 64 inches^2 is the surface area, your answer is A.
Use the following table to find the probability that a randomly chosen member of the Student Government Board is a graduate student or lives in on-campus housing. Express your answer as a fraction in lowest terms or a decimal rounded to the nearest millionth.
Students on the Student Government Board
On-Campus Housing Off-Campus Housing
Freshman 2 2
Sophomore 2 4
Junior 0 3
Senior 4 2
Graduate Student 2 0
Answers
The probability that a randomly chosen member of the Student Government Board is a graduate student or lives in on-campus housing is 8/25 or 0.32 (rounded to the nearest millionth).
1. Calculate the total number of students on the Student Government Board by summing up the numbers in the table:
Total Students = 2 + 2 + 2 + 4 + 0 + 3 + 4 + 2 = 19
2. Calculate the total number of graduate students on the Student Government Board:
Total Graduate Students = 2 + 0 = 2
3. Calculate the total number of students living in on-campus housing:
Total On-Campus Housing = 2 + 2 + 0 + 4 + 2 = 10
4. Calculate the probability of selecting a graduate student from the Student Government Board by dividing the total number of graduate students by the total number of students:
Probability of Graduate Student = Total Graduate Students / Total Students = 2 / 19
5. Calculate the probability of selecting a student living in on-campus housing by dividing the total number of students in on-campus housing by the total number of students:
Probability of On-Campus Housing = Total On-Campus Housing / Total Students = 10 / 19
6. Calculate the probability that a randomly chosen member of the Student Government Board is a graduate student or lives in on-campus housing by summing up the probabilities from steps 4 and 5:
Probability = Probability of Graduate Student + Probability of On-Campus Housing = 2 / 19 + 10 / 19
7. Simplify the fraction if necessary. In this case, the fraction cannot be simplified further, so the final probability is 2 / 19 + 10 / 19 = 12 / 19.
8. Convert the fraction to a decimal by dividing the numerator by the denominator: 12 / 19 ≈ 0.631578947, which rounds to 0.632 (rounded to the nearest thousandth).
9. Finally, express the probability as a fraction in lowest terms: 12 / 19 is already in lowest terms.
Therefore, the probability that a randomly chosen member of the Student Government Board is a graduate student or lives in on-campus housing is 12/19 or approximately 0.632 (rounded to the nearest thousandth).
For more such questions on probability, click on:
https://brainly.com/question/31048927
#SPJ8
What numbers are between 2/10 and 75% on a number line?
Answers
75% = 0.75
Some numbers between 0.25 and 0.75 are 0.5, 0.62, 3/10
12. After 2 hours, Morgan had earned $12.75 at her lemonade stand. After 5
hours, she had earned $44.25. Assuming a linear function, write an
equation in the form y=mx+b that shows the profit earned from selling
lemonade for x hours.
Answers
Answer:
y = 10.5x - 8.25
Step-by-step explanation:
m = (44.25 - 12.75)/(5 - 2) = 10.5
y = mx + b
y = 10.5x + b
12.75 = 10.5 × 2 + b
b = -8.25
y = 10.5x - 8.25
PLSSSSS ILL DO ANYTHING!!!

Answers
Answer:
Part a)
The equation of the situation is:
y = 8xPart b)
If the recipe calls for 16 ounces of flour, the number of ounces of sugar will be:
x = 2Step-by-step explanation:
Part a) Determining the equation
Given the number of ounces of flour 'y' is proportional to the number of ounces of sugar 'x'.
We know that when 'y' varies directly with 'x', we get the equation
y ∝ x
y = kx
Here, k is the constant of direct variation.Given
y = 48
x = 6
y = kx
k = y/x
k = 48/6
k = 8
Thus, the constant of direct variation = k = 8
Therefore, the equation that represents the equation
y = kx
substituting k = 8 in the equation
y = 8x
Therefore, the equation of the situation is:
y = 8xPart b) Determining the ounces of sugar i.e. 'x' when ounces of
flour = y = 16
Given
y = 16
k = 8
Ounces of sugar = x = ?
Using the equation
y = 8x
substituting y = 16
16 = 8x
8x = 16
dividing both sides by 8
x = 2
Therefore, if the recipe calls for 16 ounces of flour, the number of ounces of sugar will be:
x = 2Mike won 7 of his wrestling matches, lost 6 matches, and tied 2 matches. What percent of all of Mike's matches did he win?
Answers
Answer:
Mike won 46.67% of his matches
Step-by-step explanation:
Mike participated in a total of 7 + 6 + 2 = 15 matches.
The percentage of matches that Mike won can be found by diving the matches he won by the total number of matches and multiplying it by 100 to convert the decimal to a percentage.
(7/15) x 100% ≈ 46.67%
Therefore, Mike won approximately 46.67% of his matches.
Mike won 46.67% of all of his matches.
What is a percentage?A ratio or value that may be stated as a fraction of 100 is called a percentage. Moreover, it is indicated by the symbol "%."
The total number of matches that Mike wrestled is:
Total matches = number of matches won + number of matches lost + number of matches tied
Total matches = 7 + 6 + 2
Total matches = 15
To find the percentage of matches that Mike won, we can use the formula:
Percentage = (Number of matches won / Total number of matches) x 100%
Plugging in the values we know, we get:
Percentage = (7 / 15) x 100%
Percentage = 0.4667 x 100%
Percentage = 46.67%
Therefore, the Percentage = 46.67%.
To learn more about the percentage;
https://brainly.com/question/24159063
#SPJ5
The equation gives the position s = f(t) of a body moving
on a coordinate line (s in meters, t in seconds).
1) s = 1 + 9(cos t)
Find the body's speed at time t=pi/3 sec.
2) s = 12(sin t) - (cos t)
Find the body's velocity at time t=pi/4 sec.
Answers
Answer:
1) The velocity at this time is of \(-9\frac{\sqrt{3}}{2}\) meters per second.
2) The velocity at this time is of \(13\frac{\sqrt{2}}{2}\) meters per second.
Step-by-step explanation:
This question involves concepts of derivatives.
The velocity is the derivative of the position.
We use these following derivatives:
\((\sin{x})^{\prime} = \cos{x}\)
\((\cos{x})^{\prime} = -\sin{x}\)
1) s = 1 + 9(cos t)
Find the body's speed at time t=pi/3 sec.
We have to find the derivative at \(t = \frac{\pi}{3}\). So
\(v = (1 + 9\cos{t})^{\prime} = -9\sin{t}\)
\(v(\frac{\pi}{3}) = -9\sin{\frac{\pi}{3}}\)
\(\frac{\pi}{3}\) is a common angle, which has a sine of \(\frac{\sqrt{3}}{2}\). So
\(-9\sin{\frac{\pi}{3}} = -9\frac{\sqrt{3}}{2}\)
The velocity at this time is of \(-9\frac{\sqrt{3}}{2}\) meters per second.
2) s = 12(sin t) - (cos t)
Find the body's velocity at time t=pi/4 sec.
We have to find the derivative at \(t = \frac{\pi}{4}\). So
\(v = (12\sin{t} - \cos{t})^{\prime} = 12\cos{t} + \sin{t}\)
\(\frac{\pi}{4}\) is a common angle, which has both sine and cosine of \(\frac{\sqrt{2}}{2}\). So
\(12\cos{\frac{\pi}{4}} + \sin{\frac{\pi}{4}} = 12\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} = 13\frac{\sqrt{2}}{2}\)
The velocity at this time is of \(13\frac{\sqrt{2}}{2}\) meters per second.
Find the unit rate (constant of proportionality) of the distance traveled.
Number of hours
0.25 1.5 2.5 3
Distance traveled (km) 3 18 30 36
Answers
Answer:
12.
Step-by-step explanation:
if to re-write the given condition, then
\(\frac{3}{0.25} =\frac{18}{1.5} =\frac{30}{2.5} =\frac{36}{3} ;\)
it is clear, the required constant is 12 (12 per hour).
Need help with math homework
e^x=10^(x-1)
Answers
Answer:
Step-by-step explanation:
This equation represents the relationship between the exponential functions y = e^x and y = (10^(x-1)). These two functions are equal to each other for all values of x. This can be shown by taking the natural logarithm of both sides of the equation, which gives us:
ln(e^x) = x-1
In this equation, ln(e^x) is equal to x, since the natural logarithm of an exponential expression with a base of e is the exponent. Therefore, we can simplify the equation by taking the natural logarithm of both sides:
ln(10^(x-1)) = x-1
e^(x-1) = 10^x
The two functions e^x and 10^(x-1) are the same function with different bases, so they follow the same pattern. The fact that these two functions are equal to each other for all values of x can also be shown by graphing the two functions and seeing that they overlap perfectly.
Find y.
A. 6√3
B. 3
C. 2√3/3
D. 3√3

Answers
Answer:
B 3
notice that beside the 30 degree there is also 90 degree. please see the attachment.
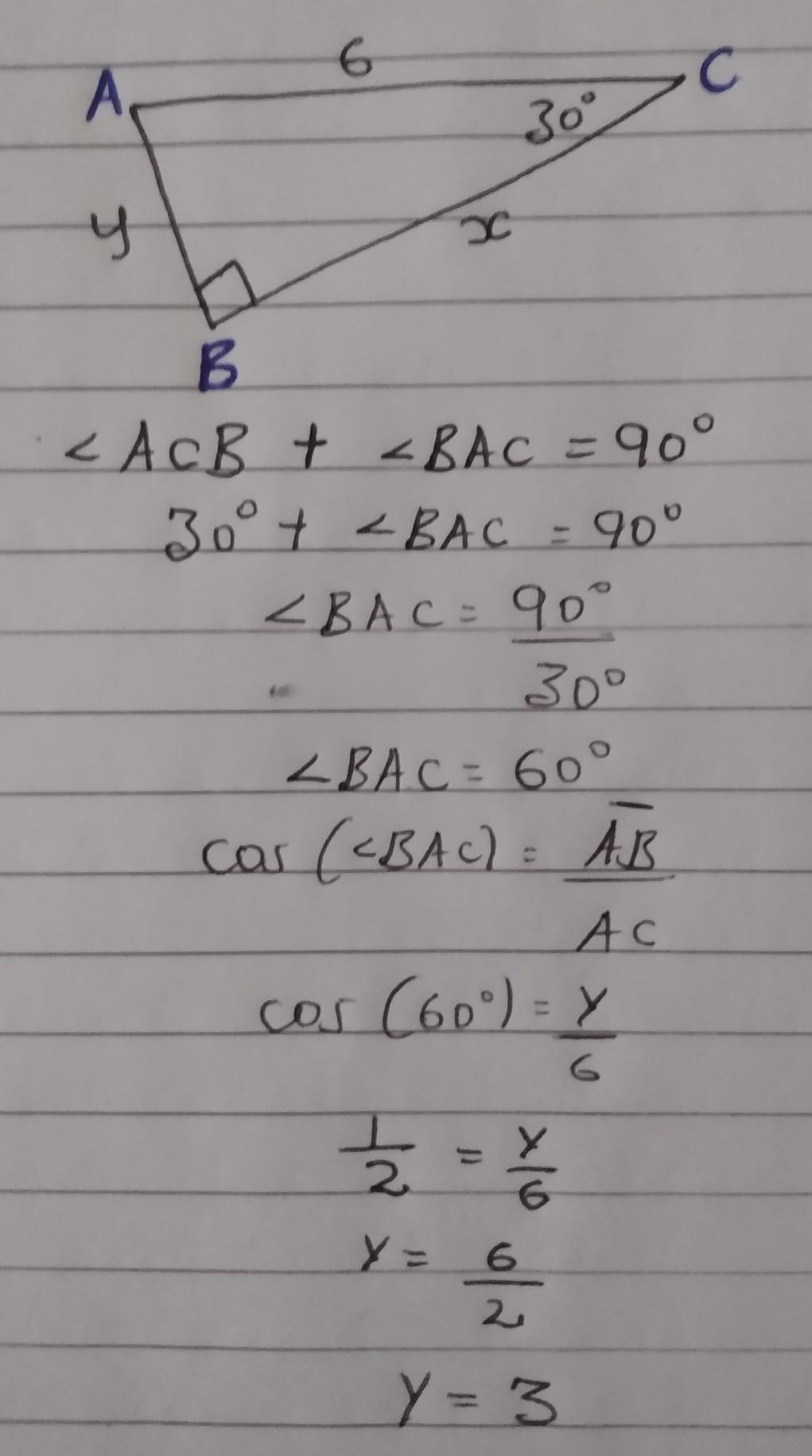
HELP PLS ASAPPP!!!
algebra problem; solving linear inequalities !!! :)
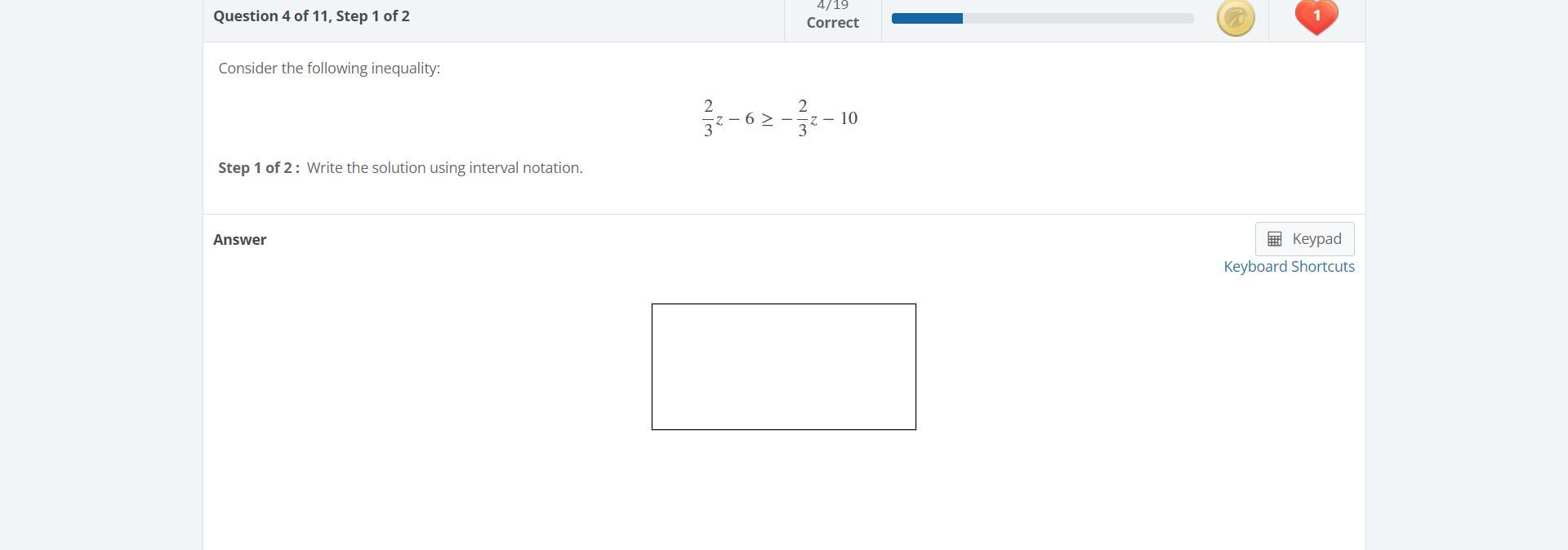
Answers
Answer: x = -3/2
Step-by-step explanation:
The mean weight of luggage checked by a randomly selected tourist-class passenger flying between two cities on a certain airline is 40 lb, and the standard deviation is 10 lb. The mean and standard deviation for a business-class passenger are 30 lb and 6 lb, respectively.
a. If there are 12 business-class passengers and 50 tourist-class passengers on a particular flight, what are the expected value of total luggage weight and the standard deviation of total luggage weight?
b. If individual luggage weights are independent, normally distributed rv’s, what is the probability that total luggage weight is at most 2500 lb?
Answers
The standard deviation of Z is \(SD(Z) = \sqrt{(Var(Z)}) \approx 73.7 lb\) and the probability that the total luggage weight is at most 2500 lb is approximately 0.9713.
a. Let X be the total luggage weight of 12 business-class passengers, and Y be the total luggage weight of 50 tourist-class passengers.
Then E(X) = 12(30) = 360, E(Y) = 50(40) = 2000
The variance of X is \(Var(X) = 12(6^2) = 432\)
and the variance of Y is
\(Var(Y) = 50(10^2) = 5000\)
By linearity of expectation, the expected value of the total luggage weight Z = X + Y is E(Z) = E(X) + E(Y) = 2360
The variance of Z is Var(Z) = Var(X) + Var(Y) = 5432.
Therefore, the standard deviation of Z is \(SD(Z) = \sqrt{(Var(Z)}) \approx 73.7 lb\) .
b. Let W be the total luggage weight of all passengers. W is normally distributed with mean
E(W) = E(X) + E(Y) = 2360 lb
and variance
\(Var(W) = Var(X) + Var(Y) = 5432 lb^2\)
The standard deviation of W is \(SD(W) = \sqrt{(Var(W)}) \approx 73.7 lb\)
Then, the probability that the total luggage weight is at most 2500 lb is P(W ≤ 2500) = P[(W - E(W))/SD(W) ≤ (2500 - 2360)/73.7] ≈ P(Z ≤ 1.90), where Z is a standard normal random variable. Using a standard normal table or calculator, we find that P(Z ≤ 1.90) ≈ 0.9713.
Therefore, the probability that the total luggage weight is at most 2500 lb is approximately 0.9713.
Learn more about variance :
https://brainly.com/question/13708253
#SPJ4