Kim accidentally leaves the water hose running for half a day the graph represents the loss of water during that time
Answers
fifijfjgjgfghj
Step-by-step explanation:
Answer:
We need to see the graph to help you
Step-by-step explanation:
Related Questions
Fatima conducts emissions inspections on cars. She finds that 6\%6%6, percent of the cars fail the inspection. Let ccc be the number of cars fatima inspects until a car fails an inspection. Assume that the results of each inspection are independent.
Answers
The probability that the first failed inspection occurs on Fatima's 5th inspection i.e P(c = 5) is 0.05..
Geometric probability distribution:In probability and statistics,the geometric distribution defines the probability of the first success occurring after k trials. The probability of success is p
P r ( X = k ) = ( 1 − p )⁽ᵏ⁻¹⁾ p.
We have given that,
An emissions inspections on cars is conducted by Fatima.
Probability that car fail the inspection, p = 6% = 0.06
let c denoted the number of cars that are inspected until one car fail to inspection.
The random variable c here. Here c follow geometric probability distribution with probability of success (0.06).
Plugging all known values in above formula we get, p(c= 5) = (1-0.06)⁴ × 0.06
= (0.94)⁴ (0.06)
=0.0468449376~ 0.05
so, the answer is 0.05
To learn more about Geometric probability distribution, refer:
https://brainly.com/question/18096310#SPJ4
Complete question:
Fatima conducts emissions inspections on cars. She finds that 6%, percent of the cars fail the inspection. Let C be the number of cars Fatima inspects until a car fails an inspection. Assume that the results of each inspection are independent.
Required:
Find the probability that the first failed inspection occurs on Fatima's 5th inspection
Use the drawing tool(s) to form the correct answer on the provided number line. Will brought a 144-ounce cooler filled with water to soccer practice. He used 16 ounces from the cooler to fill his water bottle. He then took out 16 plastic cups for his teammates and put the same amount of water in each cup. Find and graph the number of ounces of water, x, that Will could have put in each cup.

Answers
According to the information, we can infer that the number of ounces of water, x, that Will could have put in each cup is 8 ounces.
What is the number of ounces of water "x" that Will could have put in each cup?Will initially had a cooler filled with 144 ounces of water. After using 16 ounces to fill his water bottle, there were 144 - 16 = 128 ounces of water remaining in the cooler.
Will then took out 16 plastic cups for his teammates. Since the same amount of water was put in each cup, the remaining amount of water, 128 ounces, needs to be divided equally among the cups.
Dividing 128 ounces by 16 cups gives us 8 ounces of water for each cup.
So, Will could have put 8 ounces of water in each cup.
Learn more about water in: https://brainly.com/question/28465561
#SPJ1

expand x(x-6)
..........
Answers
Answer:
X² - 6x
Step by step:
Times x by x which makes x², then x times 6 makes 6x.
You get your finally answer x²-6x
Solve each system of equations by SUBSTITUTION. Clearly identify your solution.2x + 5y = -7 7x + y = -8
Answers
The solution of the system of equations are;
⇒ x = - 1 and y = - 1
What is substitution method?
To find the value of any one of the variables from one equation in terms of the other variable is called the substitution method.
Given that;
The system of equation is,
⇒ 2x + 5y = - 7
⇒ 7x + y = - 8
Now,
Solve the system of equation as;
⇒ 2x + 5y = - 7 ... (i)
⇒ 7x + y = - 8 .. (ii)
Multiply by 5 in equation (ii) and subtract from (i), we get;
⇒ 2x + 5y - 35x - 5y = - 7 + 40
⇒ - 33x = 33
⇒ x = - 1
And, 2x + 5y = -7
⇒ 2 × -1 + 5y = -7
⇒ - 2 + 5y = - 7
⇒ 5y = - 7 + 2
⇒ 5y = - 5
⇒ y = - 1
Thus, The solution of the system of equations are;
⇒ x = - 1 and y = - 1
Learn more about the system of equation visit:
https://brainly.com/question/13729904
#SPJ1
the radius of a bubble increases by 4%. Calculate the percentage increase in its (a) surface area (b) volume (to three significant figures )
Answers
Answer:
Step-by-step explanation:
Given that the radius of a bubble increases by 4%.
Let r be the radius of the spherical bubble, so the new radius of the sphere
\(R= r+0.04r = 1.04r\cdots(i)\)
(a) Surface area of the bobble,
\(s=4\pi r^2\)
So, the rate of increase of surface area = \(4\pi R^2 -4\pi r^2= 4\pi(R^2-r^2)\)
The percentage change in the surface area \(= \frac {4\pi(R^2-r^2)}{4\pi r^2}\times 100\)
By using equation (i)
The percentage change in the surface area = \(\frac {(1.04r)^2-r^2}{ r^2}\times 100\)
\(=(1.04^2-1)\times 100\)
=8.160%
Therefore, the percentage change in the surface area is 8.160%
(b) The volume of the sphere = \(4/3 \pi r^3\)
So, the change in the volume = \(4/3 \pi R^3-4/3 \pi r^3\)
Percentage change in the volume =
\(\frac {4/3 \pi R^3-4/3 \pi r^3}{4/3 \pi r^3}\times 100\)
\(=(1.04^3-1)100\) [by using equation (i)]
=12.486%
Therefore, the percentage change in the volume is 12.486%.
5+8x<3(2x+4) what’s the answer to that equation?
Answers
Answer:
Let us now solve the inequality:
5 + 8x < 3(2x + 4)
To begin, we will simplify the right side:
5 + 8x < 6x + 12
The variable on one side will then be isolated by subtracting 6x from both sides:
5 + 2x < 12
Then we'll take 5 off each sides:
2x < 7
Finally, split both sides by two:
x < 3.5
As a result, the solution to the inequality is x 3.5.
Please help!!
If you could explain that would be great!

Answers
Answer:
It would be 1/2
Step-by-step explanation:
y = (1/2)x has the format y = kx, where k is the const. of prop. In this particular case that const. of prop. is (1/2).
johanna balanced a triangle flat on her finger tip. what point of the triangle must johanna be touching?
Answers
If the triangle is not precisely symmetrical, or if Johanna's fingertip is not exactly at the centroid, she may be touching another point on the triangle, allowing her to balance it.
What precisely is a triangle?A triangle is a closed, two-dimensional geometric shape made up of three line segments known as sides that intersect at three points known as vertices. Triangles are differentiated by thier sides and angles. Triangles can be collinear (all sides equal), rotationally symmetric, or scalene dependent on their sides. Triangles are classed as keen (all angles less than 90 degrees), correct (all angle equal to 90 degrees), or indifferent (all angles greater than 90 degrees). The area of a triangle may be determined by applying the equation A = (1/2)bh, where A is just the area, b seems to be the right triangle base, and h is the triangle's height.
If the triangle is a flat, two-dimensional object, Johanna must be touching the place where the triangle's centre of mass connects with its plane. This is known as the triangle's centroid, and it is positioned at the intersection of the triangle's medians.
If Johanna can balance the triangle exactly on her fingertip, she is most likely touching the triangle's centroid. If the triangle is not precisely symmetrical, or if Johanna's fingertip is not exactly at the centroid, she may be touching another point on the triangle, allowing her to balance it.
To know more about triangle visit:
https://brainly.com/question/2773823
#SPJ1
Use the z-score formula, x-μ Z = -, and the information below to find the mean, 0 μ. Round your answer to one decimal place, if necessary. z = 2.25, x = 22.2, and = 1.6
Answers
The mean is 18.6.
Given the following information; z = 2.25, x = 22.2, and σ = 1.6, to find the mean, we have to apply the formula for z-score. z = (x - μ)/σWhere; z-score is represented by z, the value of X is represented by x, the mean is represented by μ and the standard deviation is represented by σSubstituting the values into the equation above;2.25 = (22.2 - μ)/1.6Multiplying both sides of the equation by 1.6, we have;1.6(2.25) = (22.2 - μ)3.6 = 22.2 - μ Subtracting 22.2 from both sides of the equation;3.6 - 22.2 = - μ-18.6 = - μ Multiplying both sides of the equation by -1, we have;μ = 18.6
Simply said, a z-score, also known as a standard score, informs you of how far a data point is from the mean. Technically speaking, however, it's a measurement of how many standard deviations a raw score is from or above the population mean.
You can plot a z-score on a normal distribution curve. Z-scores range from -3 standard deviations, which would fall to the extreme left of the normal distribution curve, to +3 standard deviations, which would fall to the far right. You must be aware of the mean and population standard deviation in order to use a z-score.
The z-score can show you how that person's weight compares to the mean weight of the general population.
Know more about mean here:
https://brainly.com/question/29141288
#SPJ11
Please help! (Look at image)

Answers
Answer:
27/49
Step-by-step explanation:
look image
Red

Answer:
21^84/21^9
Step-by-step explanation:
you multiply the base and you will get 21 Then you multiply the two exponents 7 and 4 is 28. then multiply 28 times 3 is 84 and the denominator stay the same
Sally invests £8000 in a savings account.
The account pays 2.8% compound interest per year.
Work out the value of her investment after 4 years.
Give your answer to the nearest penny.
Answers
The value of her investment at compound interest after 4 years will be £8934.34.
What is compound interest?
Compound interest is the adding of interest to the principle sum of a loan or deposit, or interest on interest plus interest. It is the outcome of making an investment interest, or adding it to the lent assets, rather than repaying it out or requesting return from the borrower, so that interest is received on the principle sum plus previously accrued interest in the next month. In finance and economics, compound interest is the norm. Compound interest differs from simple interest in that previously accrued interest is not added to the main amount of the current month, resulting in no compounding. The simple annual interest rate is calculated by multiplying the interest amount per period by the number of periods per year.
Given,
Principal (P) = £8000
Rate of interest (r) = 2.8% compound interest p.a.
Time (n) = 4 years
Then, according to compound interest compounded annually,
Amount = P(1+r/100)ⁿ
= 8000(1+2.8/100)⁴
= 8000(102.8/100)⁴
= 8934.34
Hence, the value of her investment at compound interest after 4 years will be £8934.34.
To know more about compound interest, click on the link
https://brainly.com/question/21441517
#SPJ9
The sum of the ages of Farhan and his cousin is 38. Seven years ago, Farhan
was thrice as old as his cousin.Find Farhan's present age.
Answers
Answer:
25 and 13
Step-by-step explanation:
sum of ages of Farhan and his cousin = 38
7 years ago Farhan thrice of his cousin = 3:1
7 year ago the sum of their ages = 38-14 = 24( 7 years for each)
3:1 = 4 units = 24
1 unit =6
ages of Farhan and his cousin 7 years ago = 6*3= 18 and 6*1 = 6
so the present age of Farhan = 18+7 = 25 and his cousin 6+7 = 13
A car is traveling down a highway at a constant speed, described by the equation d = 65t, where d represents the distance, in miles, that the car travels at this speed in t hours.
a. What does the 65 tell us in this situation?
The car travels
miles in 1 hour.
b. How many miles does the car travel in 1.5 hours?
The car travels
miles in 1.5 hours.
c. How long does it take the car to travel 26 miles at this speed?
It takes the car
hours to travel 26 miles.
Answers
(a) 65 means the car will travel 65 miles in 1 hour .
(b) The car will travel 97.5 miles in 1.5 hours .
(c) The car will take 0.4 hours to travel 26 miles at his speed .
In the question ,
it is given that
the car is traveling down a highway at a constant speed
and the equation representing is d =65*t
Part(a)
On comparing , the given equation with the equation of speed , time and distance
which is , distance = speed × time
on comparing both the equations , we get speed = 65 mph .
hence , 65 means the car will travel 65 miles in 1 hour .
Part(b)
substituting the value t = 1.5 hours in the given equation , we get
d = 65×1.5
= 97.5
hence , The car will travel 97.5 miles in 1.5 hours
Part(c)
Substituting the value of d = 26 miles in the given equation , we get
26 = 65×t
t = 26/65
t = 0.4 hours
hence , It takes the car 0.4 hours to travel 26 miles.
Therefore , (a) 65 means the car will travel 65 miles in 1 hour .
(b) The car will travel 97.5 miles in 1.5 hours .
(c) The car will take 0.4 hours to travel 26 miles at his speed .
Learn more about Equations here
https://brainly.com/question/14355020
#SPJ1
What is the value of the t score for a 99% confidence interval if we take a sample of size 20?
A. 2.845
B. 2.861
C. 3.552
D. 3.579
Answers
Answer:
2.861
Step-by-step explanation:
What is the value of the t score for a 99% confidence interval if we take a sample of size20? Thus, the t-score for a 99% confidence interval for sample size 20 is 2.861.
A walkway is being constructed using square cement tiles that each have an area of 19.0 ft2. 6 tiles will be lined up end to end to construct the walkway. What is the total length of the walkway? Round your answer to the nearest tenth of a foot. Your Answer:
Answers
Answer:
26.3 feet
Step-by-step explanation:
We have to first find the length of the side of each tile.
The area of each tile is 19.2 \(ft^2\).
The area of a square is:
A = \(L^2\)
where L = length of side
Therefore:
\(19.2 = L^2\\\\L = \sqrt{19.2} = 4.38 feet\)
6 tiles will be lined end to end to construct the walkway, hence, the length of the walkway is:
6 * 4.38 ≅ 26.3 feet
subsitute 9x-2y=14 7x+3y=20
Answers
Answer:
hope it helps you..........

Consider the initial value problem: y00 + y0−2y = 0, y(0) = 2, y0(0) = β a For which value of β does the solution satisfy limt→[infinity]y(t) = 0 ? b For which value(s) of β is the solution y(t) never = 0 for all t? That is, for which value(s) of β does the graph of the solution, y(t), never touch the t−axis?
Answers
a) To find the value of β that satisfies limt→[infinity]y(t) = 0, we can first find the general solution of the differential equation. So the value(s) of β for which the solution y(t) is never equal to 0 for all t is \(β ∈ (-∞, -2) U (-2/3, ∞)\)
The characteristic equation is \(r^2 + r - 2 = 0\), which has roots r = 1 and r = -2.
Therefore, the general solution is\(y(t) = c1e^t + c2e^-2t.\)
Using the initial conditions y(0) = 2 and y'(0) = β, we can solve for the constants c1 and c2:
\(c1 + c2 = 2\)
\(c1 - 2c2 = β\)
Solving this system of equations, we get \(c1 = 2 - β/3\) and \(c2 = β/3.\)
Therefore, the solution is y(t) =\((2 - β/3)e^t\) + \(β/3)e^-2t\). To satisfy limt→[infinity]y(t) = 0, we need the coefficient of e^t to be 0, which gives us 2 - β/3 = 0. Solving for β, we get β = 6.
So the value of β that satisfies limt→[infinity]y(t) = 0 is β = 6.
b) To find the value(s) of β for which the solution y(t) is never equal to 0 for all t, we can use the fact that the discriminant of the characteristic equation determines the nature of the roots.
In this case, the characteristic equation is r^2 + r - 2 = 0, which has roots r = 1 and r = -2. These are distinct real roots, so the general solution is y(t) = \(c1e^t + c2e^-2t.\)
For y(t) differential equation to never be equal to 0 for all t, we need both constants c1 and c2 to be nonzero. Using the initial condition y(0) = 2, we get c1 + c2 = 2.
Using the second initial condition y'(0) = β, we get c1 - 2c2 = β.
Solving these equations, we get \(c1 = (2β + 4)/5\) and \(c2 = (6 - β)/5.\)
Therefore, y(t) is never equal to 0 for all t if and only if both c1 and c2 are nonzero, which is true if and only if the coefficients satisfy the inequality (2β + 4)(6 - β) ≠ 0. Solving this inequality, we get \(β ∈ (-∞, -2) U (-2/3, ∞).\)
To learn more about differential equation, visit here
https://brainly.com/question/31583235
#SPJ4
I need help with this math problem please! At a basketball game, 55% of people attending were supporting the home team, while 45% were supporting the visiting team. If the total number of people attending the game was 520, how many people attending were supporters of the home team?
Answers
Answer: 500
Step-by-step explanation: 275/55%=275/0.55=500
With Hurtz Rent-A-Car, you can rent a car for $60 a week plus 25 cents for each mile driven. Upto how many miles can you drive if you have $272.5?
1. If p is the number of miles driven, then the cost of renting the car in dollars is
2. What is the inequality?
3. You can drive up to miles?
Answers
Answer:
p+0.25=272.5
Step-by-step explanation:
just add 0.25 on both off the equation
Please help!!
Find the measure of the arc or angle indicated.
A. 60°
B. 90°
C. 30°
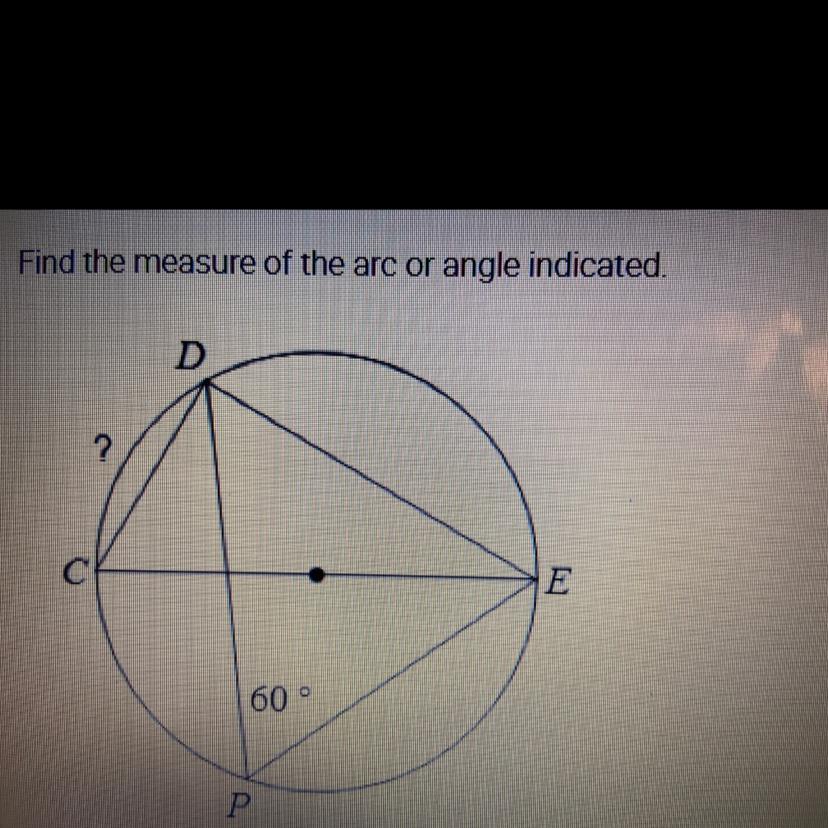
Answers
Answer: A
Step-by-step explanation:

Solve: (5x - 3y + 2z)²
Answers
Answer:
25\(x^{2}\) - 30xy + 20xz + 9\(y^{2}\) - 12yz + 4\(z^{2}\)
Step-by-step explanation:
We multiply it out.
(5x - 3y + 2z) * (5x - 3y + 2z)
5x*5x + 5x*-3y + 5x*2z - 3y*5x - 3y*-3y -3y*2z + 2z*5x +2z * -3y +2z *2z
25\(x^{2}\) - 15xy + 10xz - 15xy + 9\(y^{2}\) - 6yz + 10xz - 6yz + 4\(z^{2}\)
Add like terms
25\(x^{2}\) - 15xy - 15xy + 10xz + 10xz + 9\(y^{2}\) - 6yz - 6yz + 4\(z^{2}\)
25\(x^{2}\) - 30xy + 20xz + 9\(y^{2}\) - 12yz + 4\(z^{2}\)
HELP ME!!! I WILL GIVE BRAINLIEST AND 15 POINTS!!!!!!!!
Evaluate each expression for n = 3, p = 10.5, t = -2, y = 4.
Solve
1.) 3n + 2t
2.) ny - 6 + p
Answers
9-4
5
2) (3)(4)-6+10.5
12-6+10.5
6+10.5
16.5
Therefore, the solution to #1 is 5, and the solution to #2 is 16.5.
2. 16.5
Plug in the values and solve.
Please help me with 12,13,14 please and thank you!

Answers
Hope this helps! xoxo

Help, this is Math.
Dividing fractions

Answers
Step-by-step explanation:
don't panic. just breathe and then use common sense.
1.
1 math question in 1/200 second
2 minutes have 2×60 seconds = 120 seconds.
each of the seconds has 200 1/200 seconds.
so, in 2 minutes we have
120 × 200 time units to finish math questions.
in each time unit 1 math question can be answered.
120×200 = 24,000
the computer can answer 24,000 math questions in 2 minutes.
2.
it can run for 15 minutes.
15 minutes have
15×60 = 900 seconds (as every minute has 60 seconds)
it can vacuum 1/2 ft² in 1 seconds.
in 900 seconds it can then vacuum 900×1/2 = 450 ft².
so, yes, it can clean 400 ft² without recharging.
Can a triangle can have sides with lengths 2.7, 3.5, and 9.8.
Answers
Answer: No
Step-by-step explanation:
2.7 + 3.5 is not greater than 9.8.
Answer:
no It cant
Step-by-step explanation:
2.7 + 3.5 is not greater than 9.8.
Pls answer anything you know here (Factoring) thanks

Answers
Answer:
Find the GCF and put it outside parentheses...then put the rest of digits in parentheses.
Step-by-step explanation:
1. 2a(b+c-1)
2. y^3(y^2+1)
3. 4(5x^2-3)
identify the equation for the line tangent to the circle x2 y2 = 169 at the point (−5, 12).
Answers
The equation for the line tangent to the circle \(\(x^2 + y^2 = 169\)\) at the point \(\((-5, 12)\)\) is \(\(x + 5y = 13\)\).
To find the equation of the tangent line to the circle at a given point, we need to determine the slope of the tangent line and its point of tangency. The slope of the tangent line is equal to the negative reciprocal of the derivative of the circle's equation with respect to x.
Differentiating the equation \(\(x^2 + y^2 = 169\)\) with respect to x, we get \(\(2x + 2y \frac{{dy}}{{dx}} = 0\)\). Rearranging this equation, we find \(\(\frac{{dy}}{{dx}} = -\frac{{x}}{{y}}\)\).
Substituting the coordinates of the given point (-5, 12) into the derivative, we have \(\(\frac{{dy}}{{dx}} = -\frac{{-5}}{{12}} = \frac{{5}}{{12}}\)\).
Since the tangent line has the same slope as the derivative at the point of tangency, the slope of the tangent line is \(\(\frac{{5}}{{12}}\)\).
Using the point-slope form of a line, \(\(y - y_1 = m(x - x_1)\)\), where \(\((x_1, y_1)\)\) is the given point, we substitute \(\((-5, 12)\)\) and the slope \(\(\frac{{5}}{{12}}\)\) to obtain \(\(y - 12 = \frac{{5}}{{12}}(x + 5)\)\).
Simplifying this equation, we get \(\(x + 5y = 13\)\), which is the equation of the tangent line to the circle at the point \(\((-5, 12)\)\).
To learn more about tangent refer:
https://brainly.com/question/30385886
#SPJ11
what is 4 x 3 - 3 +3
Answers
4 x 3= 12
12-3= 9
9+3=12
12x+-3+3
(12x)+(-3+3)
=12x
find the slope of the line passing through the points (8,2) and (8,-5)
Answers
Step-by-step explanation:
m=y-y¹/x-x¹
=-5-2/8-8
=-7/1
=-7
Answer:
slope 0
Step-by-step explanation:
-5-2/8-8
-7/0
x=0
horizontal line
Solve for xxx. Enter the solutions from least to greatest. 3x^2 - 9x - 12 = 03x
2
−9x−12=0
Answers
The solutions to the equation 3x^2 - 9x - 12 = 0 are x = 4 and x = -1.
To solve the quadratic equation 3x^2 - 9x - 12 = 0, we can use the quadratic formula:
x = (-b ± √(b^2 - 4ac)) / (2a),
where a, b, and c are the coefficients of the quadratic equation.
In this case, a = 3, b = -9, and c = -12. Substituting these values into the quadratic formula, we have:
x = (-(-9) ± √((-9)^2 - 4 * 3 * (-12))) / (2 * 3)
= (9 ± √(81 + 144)) / 6
= (9 ± √(225)) / 6
= (9 ± 15) / 6.
We have two possible solutions:
For the positive root:
x = (9 + 15) / 6
= 24 / 6
= 4.
For the negative root:
x = (9 - 15) / 6
= -6 / 6
= -1.
The solutions to the equation 3x^2 - 9x - 12 = 0 are x = 4 and x = -1.
for such more question on equation
https://brainly.com/question/17145398
#SPJ8