Kyla spends 60 minutes of each day exercising. Let be the number of days that Kyla exercises, and let represent the total minutes of exercise in a given time frame. Show the relationship between the number of days that Kyla exercises and the total minutes that she exercises.
What is the independent variable?
Answers
Answer:
t=60d d is the independent variable
Step-by-step explanation:
Answer
The independent variable is the number of days that Kyla exercises.
Step-by-step explanation:
Related Questions
find the volume of a pyramid whose base is a square of side 8 and height of 20. use cross sections that are perpendicular to the y-axis.
Answers
The answer is 427.7
To find the volume of a pyramid with a square base of side 8 and a height of 20, we need to follow these steps:
Step 1: Identify the formula for the volume of a pyramid. The formula is V = (1/3)Bh, where V is the volume, B is the area of the base, and h is the height.
Step 2: Calculate the area of the square base. Since the base is a square with a side length of 8, its area is 8 x 8 = 64 square units.
Step 3: Plug the values into the formula. Using the area of the base (B = 64) and the height (h = 20), we can now find the volume: V = (1/3)(64)(20).
Step 4: Calculate the volume. V = (1/3)(64)(20) = 64/3(20) = 1280/3 cubic units.
So, the volume of the pyramid is 1280/3 cubic units.
Learn more about volume of the pyramid : https://brainly.com/question/218706
#SPJ11
Show that one zero of 8x230x27 is the square of the other.
Answers
Answer:
8x2-30x+27 has one root (9/4) the square of the other (3/2)
Step-by-step explanation:
8x2+30x+27 = (2*x+3)*(4*x+9) => solution = {-3/2, -4/9}
One is not the square of the other because squares are positive.
8x2-30x+27 = (2*x-3)*(4*x-9) =>
solution = {3/2, 4/9} since (4/9 = (3/2)^2, therefore the preceding question is correct.
Given:
R is the midpoint of QS
Prove: PRQ = TRS

Answers
Answer:
Step-by-step explanation: Hello!
I don't remember all of the postulates to these, but I hope this will help you! Vertical angles are congruent, so both angles SRT and PRQ are congruent. This also means that line segments PQ and ST are congruent. You also know that angles Q and S are congruent which is given. By the ASA Theorem, when two angles and a side are congruent, then the triangles are congruent.
the process of finding the derivative of a function is called____.
Answers
The process of finding the derivative of a function is called differentiation.
Differentiation is a fundamental concept in calculus that involves determining the rate at which a function changes with respect to its independent variable. It allows us to analyze the behavior of functions, such as finding slopes of curves, identifying critical points, and understanding the shape of graphs.
The derivative of a function represents the instantaneous rate of change of the function at any given point. It provides information about the slope of the tangent line to the graph of the function at a specific point.
The notation used to represent the derivative of a function f(x) with respect to x is f'(x) or dy/dx. The derivative can be interpreted as the limit of the difference quotient as the interval approaches zero, representing the infinitesimal change in the function.
By applying differentiation techniques, such as the power rule, product rule, chain rule, and others, we can find the derivative of a wide range of functions. Differentiation is a powerful tool used in various areas of mathematics, physics, engineering, economics, and other fields to analyze and solve problems involving rates of change.
To learn more about differentiation
https://brainly.com/question/954654
#SPJ11
Determine whether the infinite geometric series converges or diverges. If it converges, find the sum, and if it diverges then explain why.
48 + 36 + 27 + 81/4 + ...
Answers
Geometric series means
|r|<1Lets spot out common ratio
36/48=3/427/36=3/4Its less than 1
Hence series converges
Sum:-
a/1-r48/(1-3/4)48/1/4192Answer:
Series converges
Sum = 192
Step-by-step explanation:
General form of geometric series: \(a_n=ar^{n-1}\)
where:
a is the initial termr is the common ratioGiven series: 48, 36, 27, 81/4, ...
\(\implies a = 48\)
\(\implies r=\dfrac{a_2}{a_1}=\dfrac{36}{48}=\dfrac34\)
Geometric series converges when |r| < 1
Geometric series diverges when |r| ≥ 1
\(\textsf{As }r=\dfrac34\ \implies|\dfrac34| < 1\:\implies\:\textsf{series converges}\)
Sum of an infinite geometric series:
\(S_\infty=\dfrac{a}{1-r}\quad\textsf{for}\:|r| < 1\)
Substituting values of a and r:
\(\implies S_\infty=\dfrac{48}{1-\frac34}=192\)
If n = 3, what is the value of 6n – 3?
A. 12
B. 15
C. 57
D. 60
Answers
Answer:
B. 15
Step-by-step explanation:
6×3= 18
18-3= 15
.........
Answer:
15 or B
Step-by-step explanation:
6(3) - 3 = 15
18 - 3 = 15
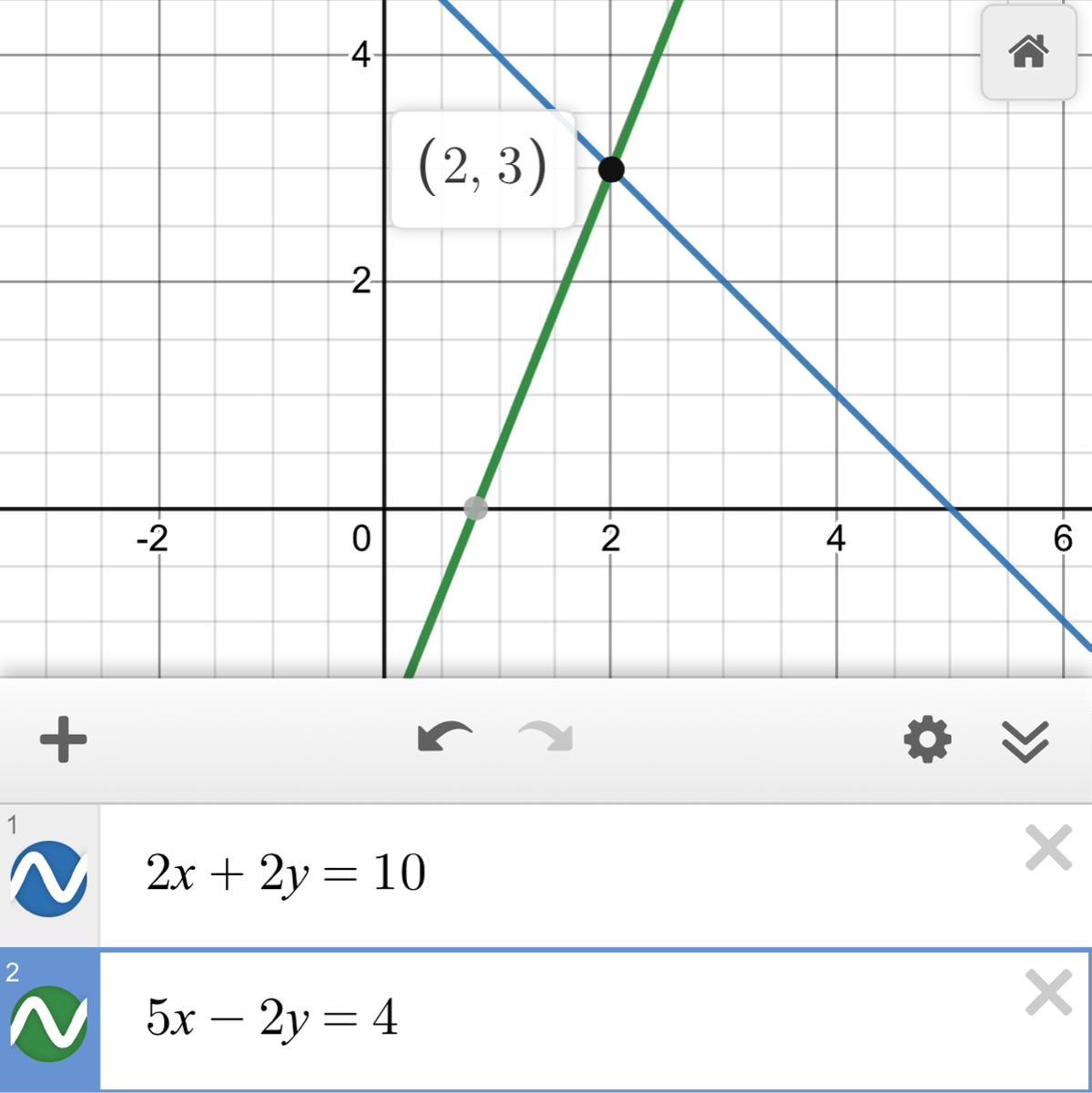
2x +2y =10 5x -2=4
What is the solution of the system of equations?
A (3,2)
B (2,3)
C (-2,-7)
D(2,7)
Answers
Step by step
Given
2x + 2y = 10
5x -2y = 4
We can use elimination to solve
We see +2y and -2y will cancel each other out and we can then add the equations together and solve for x
2x + 2y = 10
5x -2y = 4
7x = 14
Divide both sides by 7 to solve for x
7/7 x = 14/7
x = 2
Substitute the value of x = 2 into the first equation to solve for y
2x + 2y = 10
2(2) + 2y = 10
4 + 2y = 10
Subtract 4 from both sides to isolate y
4 - 4 + 2y = 10 -4
Simplify
2y = 6
Divide both sides by 2 to solve for y
2/2 y = 6/2
y = 3
So x=2, y=3
I graphed it to check and prove it is correct
Question
On 34 acres of land, there are a
total of 3,434 trees.
If the trees are spread out
evenly, how many trees are on
each acre of land?
This seems like it’s easy but it’s not really clicking. Please help and thank you!
Answers
The number of trees on each acre of land, given that the trees are evenly spaced out, is 101 trees per acre
How to find the number of trees ?To find out how many trees are on each acre of land, we need to divide the total number of trees by the number of acres. This is given that the trees are spread out evenly as is the case here.
The number of trees per acre of land is therefore:
= Number of trees in total / Number of acres
= 3, 434 / 34
= 101 trees per acre
Find out more on acres at https://brainly.com/question/19783923
#SPJ1
Anyone can help me on this

Answers
Answer:
f(1)=5 f(0)=0 f(-1)=-3
Step-by-step explanation:
by pluging it in.
A company sells phone cases for $15 each. At the end of the week, they have sold $570 worth of phone cases. How many phone cases did they sell? Write and solve an equation to find the answer.
a. What is the equation that represents this problem?
b. How many phone cases did they sell?
Answers
Answer:
They sold 38 phone cases.
Step-by-step explanation:
The equation I used to solve is
\(570 \div 15\)
Express the ratio 75:4 in simplest form
Answers
by simplifying the number by 2 & 4 we get
=> 75:4
=> 37.5:2
=> 18.75:1
the simplest form of the numbers in ratio is 18.75 : 1...
hope this helps u out and Mark the brainliest :)
The following data represent the record high temperatures for each of the 50 states. 112 100 127 120 134 118 105 110 109 112 110 118 117 116 118 122 114 114 105 112 107 112 114 115 118 117 118 122 106 110 116 108 110 121 113 120 119 111 104 111 120 113 120 117 105 110 118 112 114 144 a. Construct the stem and leaf plot.
b. Construct a frequency distribution table with 4 classes.
c. Calculate the mean, median and mode.
d. Calculate the variance and standard deviation.
e. Calculate inter-quartile range.
Answers
a. The stem and leaf plot for the given data can be constructed to visually represent the distribution of the record high temperatures for each state.
b. A frequency distribution table with 4 classes can be created to organize the data into intervals and count the number of occurrences within each interval.
c. The mean, median, and mode can be calculated to provide measures of central tendency for the data set.
d. The variance and standard deviation can be computed to determine the spread or variability of the data.
e. The interquartile range can be calculated to measure the dispersion of the middle 50% of the data.
a. To construct the stem and leaf plot, we separate each temperature value into a stem and leaf. The stem represents the tens digit, while the leaf represents the units digit. Here is the stem and leaf plot for the given data:
10 | 4
11 | 045566677899
12 | 011224
13 | 0013334445555778
14 | 4
b. To create a frequency distribution table with 4 classes, we divide the range of the data into four equal intervals. The classes and their corresponding frequencies are as follows:
104-113: 15
114-123: 19
124-133: 7
134-143: 2
c. The mean is calculated by summing all the values and dividing by the total number of values. The median is the middle value when the data is arranged in ascending order. The mode is the value that appears most frequently in the data set. In this case:
Mean: 115.68
Median: 116
Mode: 118
d. The variance measures the average squared deviation from the mean, while the standard deviation is the square root of the variance. Using the appropriate formulas, the variance is approximately 53.75, and the standard deviation is approximately 7.33.
e. The interquartile range (IQR) is the difference between the third quartile (Q3) and the first quartile (Q1). By ordering the data and calculating the quartiles, we find:
Q1: 110
Q3: 118
IQR: 8
These calculations provide a summary of the distribution and characteristics of the given data set of record high temperatures for each state.
To learn more about frequency distribution visit:
brainly.com/question/30625605
#SPJ11
Consider an experiment with the sample space:
S = { a, b, c, d, e, f, g, h, i, j, k}
and the events
A = {a, c, e, g}
B = {b, c, f, j, k}
C = {c, f, g, h, i}
D = {a, b, d, e, g, h, j, k}
Find the outcomes in each of the following events:
A'
C'
D'
A\capB
A\capC
C\capD
Find the outcomes of the following:
( A\capB\capC)'
A\cupB\cupC\cupD
(B\cupC\cupD)'
B'\capC'\capD'
Answers
An experiment with the sample space is (A\capB\capC)' = S \ (A\capB\capC) = S \ {c} = {a, b, d, e, f, g, h, i, j, k}
A\cupB\cupC\cupD = {a, b, c, d, e, f, g, h, i, j, k}
(B\cupC\cupD)' = S \ (B\cupC\cupD) = {a, c, d, e, g, i}
Using the notation ' to represent complement and \cap to represent intersection, we have:
A' = {b, d, f, h, i, j, k}
C' = {a, b, d, e, j, k}
D' = {c, e, f, i}
A\capB = {c}
A\capC = {c, g}
C\capD = {c, f, g, h, i}
Using the fact that (X)' = S \ X, we have:
(A\capB\capC)' = S \ (A\capB\capC) = S \ {c} = {a, b, d, e, f, g, h, i, j, k}
A\cupB\cupC\cupD = {a, b, c, d, e, f, g, h, i, j, k}
(B\cupC\cupD)' = S \ (B\cupC\cupD) = {a, c, d, e, g, i}
Learn more about sample space here
https://brainly.com/question/10558496
#SPJ11
HI IVE BEEN POSTING THIS AND NO ONE IS HELPING THIS ASSIGNMENT IS DUE IN 12 MINS AND IM HAVING A HARD TIME SOLVING IT. THIS IS PYTHAGOREAN THEOREM AND I DONT GET IT WILL MARK BRAINLIEST IF SHOW WORK

Answers
Answer:
the formula is
base^2+height^2=hypotenuse^2
I hope it helps
have a nice day
if you still can't understand feel free to ask me
#Captainpower
Answer:
21
Step-by-step explanation:
Kindly check the image below to see a visual of how the question is set up.
( my apologies for the terrible handwriting lol )
Now lets look back at the question.
The question is asking us to find the total length of Jayleen and Walter's entire walk.
Essentially it's asking for the perimeter.
In order to find the perimeter we must find the length of the hypotenuse.
Notice that the image created forms a triangle with a right angle.
That being said we can use the Pythagorean Theorem to solve for the missing side length ( or the "shortcut" ) ( also note that the Pythagorean theorem only works with right triangles )
The Pythagorean theorem = \(a^2+b^2=c^2\) where a and b = legs and c = hypotenuse
The two legs = 5 and 7 and the hypotenuse = the shortcut
That being said, we plug in the given values ( a and b ) and solve for "c"
\(5^2+7^2=c^2\)
step 1: Simplify
\(5^2=25\\7^2=49\\25+49=74\)
now we have 74 = c²
step 2 take the square root of each side
\(\sqrt{74} =8.60232\\\sqrt{c^2} =c\)
we're left with c = 8.60232
This means that the shortcut that Jayleen and Walter took had a distance of 8.6
Finally we find the perimeter of the triangle
Perimeter = sum of side lengths
8.6 + 7 + 5 = 20.6
* round to the nearest whole number *
The answer would be 21

Classify the triangle: a triangle with one right angle and no congruent sides.
Enter your answer
Answers
Answer:
Scalene Traingle
Step-by-step explanation:
Because a scalene triangle has no congruent sides, but can be a right angle (90 degree)!
a rectangular prism is 9 yards long, 16 yards wide, and 6 yards high. what is the surface area of the rectangular prism?
Answers
The surface area of the rectangular prism is 588 square yards. The total region or area covered by all the faces of a rectangular prism is defined as the surface area of a rectangular prism.
It is a three-dimensional shape. It has six faces, and all the faces are rectangular-shaped. Therefore, both the bases of a rectangular prism must also be rectangles.
- Face 1: 9 yards long and 6 yards high, so its area is 9 x 6 = 54 square yards.
- Face 2: 9 yards long and 6 yards high, so its area is 9 x 6 = 54 square yards.
- Face 3: 16 yards wide and 6 yards high, so its area is 16 x 6 = 96 square yards.
- Face 4: 16 yards wide and 6 yards high, so its area is 16 x 6 = 96 square yards.
- Face 5: 9 yards long and 16 yards wide, so its area is 9 x 16 = 144 square yards.
- Face 6: 9 yards long and 16 yards wide, so its area is 9 x 16 = 144 square yards.
The surface area = 54 + 54 + 96 + 96 + 144 + 144
= 588 square yards.
Surface area of the rectangular prism is 588 square yards.
To learn more about rectangular prism visit:
https://brainly.com/question/29753475
#SPJ4
Which expression is equivalent to −12(3−25)?
Answers
Answer:
264
Step-by-step explanation:
First let's try the distributive property first
(-12x3)+(-12x-25)
-36+(300) Keep in mind that two negatives equal a positive
-36+300
264
There is another way to do this though
PEMDAS tells us to use what is in the parenthesis first so let's do that
-12(-22) 3-25 equals -22
264 Once again two negatives equal a positive
Your answer could be 264 or any one of these steps depending on what you need your answer to be but I'll put 264 as my "answer"
Answer:
what's the expression
Step-by-step explanation:
According to the u.s. census, 67.5% of the u.s. population were born in their state of residence. in a random sample of 200 americans, what is the probability that fewer than 125 were born in their state of residence?
Answers
The probability that fewer than 125 were born in their state of residence if, In the U.S. census, 67.5% of the U.S. population were born in their state of residence. In a random sample of 200 Americans, is 0.03.
What is probability?The area of mathematics known as probability deals with numerical representations of the likelihood that an event will occur or that a statement is true. An event's probability is a value between 0 and 1.
Given:
In the U.S. census, 67.5% of the U.S. population were born in their state of residence. In a random sample of 200 Americans,
Calculate the probability that fewer than 125 were born in their state of residence as shown below,
P(x < 125) = \(\int _{125} ^ \infty fxdx\)
P(x < 125) = \(1 / \sqrt{2\pi\times 6.34} e^{-1/2(x - 123.\sqrt{2}/ 6.34 )}\)
P(x < 125) =0.0344
P(x < 125) = 0.03
Thus, the probability is 0.03.
To know more about Probability:
https://brainly.com/question/743546
#SPJ4
in the township of springfield, renovating homeowners must pay a fee of $35 per square foot they add to their house past 25% of the original square footage. in springfield, eamon pays a $2,800 fee after adding 380 square feet to his home. What was the original square footage of eamon's home?
Answers
The answer calculates the original square footage of Eamon's home based on the $35 fee per square foot paid for adding 380 square feet past 25% of the original square footage. The original square footage of Eamon's home is 1,520 square feet.
Let's assume that the original square footage of Eamon's home was "x". According to the problem, he had to pay a fee of $35 for every square foot he added past 25% of the original square footage.
Therefore, the square footage he added to his home past 25% of the original square footage was:
380 - 0.25x
And the fee he paid was $2,800. So we can write an equation:
35(380 - 0.25x) = 2,800
Simplifying the equation, we get:
13,300 - 8.75x = 0
Solving for x, we get:
x = 1,520 square feet
Therefore, the original square footage of Eamon's home was 1,520 square feet.
Learn more about algebra here: brainly.com/question/24875240
#SPJ1
Which state comparing the function is true

Answers
Answer:
the slope of W is less than the slope of Z
Step-by-step explanation:
Function Z
find slope take two points (0,15.8) (1,15.76)
m=y2-y1/x2-x1
m=(15.76-15.8)/1-0
m=-0.04
the equation for function z : y=-0.04x+15.8
slope of W=-0.0625 which is less than -0.04
y intercept pf W=30, is greater than the y intercept of Z=15.8
Answer: The first statement is true.
Step-by-step explanation: The slope of function Z is -0.04 or - 1/25 The slope of function W is -0.0625 or -1/16.
Tricky! The absolute values of W are larger, but that makes the slope more negative.
What are the solutions of this graph? *

Answers
A movie theater charges $6.00 for children's tickets, and $8.75 for adult tickets. If the
movie theater made $1297.50, and there were 175 total tickets sold, how many adults
and how many children attended the movie?
Answers
(175 - x) 6 + x (8.75) = 1297.50
1050 - 6x + 8.75x = 1297.50
x = 90
y (children) = 175 - 90 = 85
Four times the sum of 5 and some number is 20. What is the number?
Answers
This is the answer to your problem

Find an equation of the line that satisfies the given conditions.
Through (-1, -2) and (4, 3)
Answers
The final equation is y =x-1.
To find the line that satisfies the given, we will use the two-point form
\(y - y_{1} = \frac{y_{2} - y_{1} }{x_{2} - x_{1} } (x - x_{1} )\)
Before we use this, however, we need to assign to the points given the variables they represent:
(-1, -2) and (4, 3)
\(x_{1} = -1\)
\(x_{2} = 4\)
\(y_{1} = -2\)
\(y_{2} = 3\)
Now, we will substitute these values
\(y - y_{1} = \frac{y_{2} - y_{1} }{x_{2} - x_{1} } (x - x_{1} )\)
⇒ \(y - (-2) = \frac{3 - (-2) }{4-(-1) } (x -(-1) )\)
⇒ \(y +2 = \frac{3 +2 }{4 +1 } (x +1 )\)
⇒ \(y +2 = \frac{5 }{5 } (x +1 )\)
⇒ \(y +2 = x +1\)
⇒ \(y = x -1\)
Thus, the final equation is y =x-1.
Read more about equations:
https://brainly.com/question/22688504
#SPJ4
Which of the following describes an example of mutually exclusive outcomes A and B for throwing a single 6-sided
die?
A = the outcome is odd, B = the outcome is 3
A = the outcome is in {1,2,3,4}, B = the outcome is in {4,5,6)
A = the outcome is odd, B = the outcome is even
A = the outcome is less than 6, B = the outcome is more than 1
Answers
A=the outcome is odd, B=the outcome is even
Is mutually exclusive because you can't have a number that is even and odd at the same time.
Hope this helps :)
WHAT IS THE PERCENT OF DECREASE FROM 1000 to 10
Answers
Answer:
(1000-10/10)%
(990/10)%
99%
please help me (help)

Answers
Step-by-step explanation:
who reported you (for no reason)?

Vikas’s mother is 22years younger than Vikas’s grandmother and 27 years older than
Vikas. The sum of their ages is 121years. Find their present ages
Answers
Their present age are:
Vikas 's age = 15 years, Mother's age = 42 years and
Grandmother's age = 64 years.
Let that present age of Vikash is x yrs.
So, his Mother's age= (x+27) yrs
Grandmother's age = (x+27+22) i.e., (x+49) yrs.
According to question,
x+ (x+27)+ (x+49) = 121
⇒ 3x+ 76 = 121
⇒ 3x = 121-76
⇒ x= 45/3
⇒ x = 15
Therefore,
x = 15
Which means the age of Vikas is 15 years.
Now
So, mother's age will be = 15+27
= 42 years.
And,
Grandmother's age = 15+49
= 64 years.
Hence, age of Vikash, his Mother and his Grandmother are 15 yrs, 42 yrs, and 64 yrs respectively.
Learn more about age:
https://brainly.com/question/91727
#SPJ4
**Due soon, pls help!**
The scale of a model car is 1 inch to 6.5 feet. What is the length, in feet of the actual car, if the model is 6 inches?
Answers
Answer:
39 feet
Step-by-step explanation:
for every 6.5 feet there is one inch
so you multiply the amount of inches by 6.5
6.5 x 6 = 39
Answer:
39
Step-by-step explanation:
Question: In A Box Plot, Data Value X Is Considered An Outlier If A. X Q1 -1. 0(IQR) Or X Q3 +1. 0(IQR) B. X Q1-1. 5(IQR) Orx> Q3+1. 5(IQR). X < Q2-1. 5(IQR) Or X > Q2+1. 5(IQR) D. X Q2-1. 0(TQR) IQR) Oc Or X>Q2+1. 0
Answers
The right response is B. According to Option B, a data value X is regarded as an outlier if it deviates from the range Q1 - 1.5(IQR) to Q3 + 1.5. (IQR).
The right response is B.
The distance between the first quartile (Q1) and the third quartile in a box plot is known as the interquartile range (IQR) (Q3).
According to Option B, a data value X is regarded as an outlier if it deviates from the range Q1 - 1.5(IQR) to Q3 + 1.5. (IQR).
Although the range given in Option A is erroneous, the idea of an outlier being outside of a specific range based on the IQR is correct.
Option C's range, which is Q2 - 1.5(IQR) to Q2 + 1.5(IQR), is incorrect for locating outliers.
The phrase "TQR," which is uncommon in box plots, is mentioned in Option D. The range of Q2 -1.0(IQR) to Q2 +1.0(IQR) provided is incorrect for either locating outliers.
Learn more about "outlier." here:
https://brainly.com/question/3779855
#SPJ4