Kyle has a storage box that is 2 ft. Long, 3 ft. High, and has a volume of 12 ft. 3 12 ft.3. Myla has a storage box that is 4 ft. High, 2 ft. Long, and has a volume of 16 ft. 3 16 ft.3. What are the widths of Kyle and Myla's boxes? Explain how you know.
Answers
Answer: The widths of Kyle and Myla's boxes is the same as 2 ft.
Step-by-step explanation:
Formula : Volume of cuboidal box = length x width x height
\(width=\dfrac{Volume}{length\times height}\)
Given: Kyle has a storage box that is 2 ft. Long, 3 ft. High, and has a volume of 12 ft³ .
\(width=\dfrac{12}{2\times3}=2\ ft.\)
Myla has a storage box that is 4 ft. High, 2 ft. Long, and has a volume of 16 ft³.
\(width=\dfrac{16}{4\times2}=2\ ft.\)
Hence, the widths of Kyle and Myla's boxes is the same as 2 ft.
Answer:
Step-by-step explanation:
Volume of cuboidal box = length x width x height
Related Questions
f(x)=2x+1/x-1 then f^-1(1)
Answers
Answer:
f⁻¹(x) = (x + 1) / (x - 2)f⁻¹(1 ) = - 2Step-by-step explanation:
Given function:
f(x) = (2x + 1) / (x - 1)Find its inverse, substitute x with y and f(x) with x, solve for y:
x = (2y + 1) / (y - 1)x(y - 1) = 2y + 1xy - x = 2y + 1xy - 2y = x + 1y(x - 2) = x + 1y = (x + 1) / (x - 2)Substitute y with f⁻¹(x):
f⁻¹(x) = (x + 1) / (x - 2)Find f⁻¹(1 ):
f⁻¹(1 ) = ( 1 + 1) / (1 - 2) = 2 / - 1 = - 2Find the product.
11 × 6.41
60.51
70.51
12.82
128.2
Answers
Answer:
Step-by-step explanation:
11 x 6.41
= 70.51
or
= 7051/100
or
=70 50/100
Write the general form of the equation of the circle. Center: (−1,4); solution point: (2,1)
Answers
Answer:
r² = (2 - (-1))² + (1 - 4)² = 3² + (-3)² = 9 + 9 = 18
(x + 1)² + (y - 4)² = 18
The general form of the equation of the circle is `(x − h)² + (y − k)² = r²`, where the center of the circle is at `(h, k)` and the radius of the circle is `r`.
Given center: `(h, k) = (-1, 4)`Given solution point: `(x, y) = (2, 1)`Let the radius be `r`.
Then, using the distance formula, we can calculate the radius `r`.Distance between center and solution point is `r`i.e. `(x − h)² + (y − k)² = r²
Plugging in the values, we get:`(2 − (-1))² + (1 − 4)² = r²`
Solving for `r`, we get:`3² + (-3)² = r²`
⇒ 18 = r²
⇒ r = ±sqrt(18)`
The center of the circle is `(h, k) = (-1, 4)` and radius of the circle is `r = ±sqrt(18)`.
Hence, the equation of the circle in the general form is`(x − (-1))² + (y − 4)² = (±sqrt(18))²`
On simplifying, we get:`(x + 1)² + (y − 4)² = 18`Therefore, the required equation of the circle in the general form is `(x + 1)² + (y − 4)² = 18`.
Thus, the equation of the circle in the general form is `(x + 1)² + (y − 4)² = 18`.
To know more about distance formula, visit
https://brainly.com/question/32846365
#SPJ11
Verify that y=-tcost-t is a solution of the initial-value problem
t dy/dt= y+t^2sint y(pi)=0
Answers
The function y = -tcost-t is a solution to the initial-value problem t(dy/dt) = y + t^2sin(t), with the initial condition y(pi) = 0.
To verify whether the given function y = -tcos(t) - t is a solution of the initial-value problem t(dy/dt) = y + t^2sin(t) and y(pi) = 0, we need to follow these steps:
Step 1: Calculate dy/dt
Differentiate y = -tcos(t) - t with respect to t to find dy/dt:
dy/dt = -cos(t) + tsin(t) - 1
Step 2: Substitute the values of y and dy/dt into the differential equation
Replace y and dy/dt in the differential equation t(dy/dt) = y + t^2sin(t) with their corresponding values:
t(-cos(t) + tsin(t) - 1) = (-tcos(t) - t) + t^2sin(t)
Step 3: Simplify the equation
Distribute t on the left side:
-tcos(t) + t^2sin(t) - t = -tcos(t) - t + t^2sin(t)
Combine like terms on both sides:
-tcos(t) + t^2sin(t) - t = -tcos(t) - t + t^2sin(t)
Step 4: Verify if the equation holds true
The equation is an identity, as the left side is equal to the right side for all values of t. Therefore, the function y = -tcos(t) - t satisfies the differential equation t(dy/dt) = y + t^2sin(t).
Step 5: Check the initial condition
We also need to verify if y(pi) = 0. Substitute pi into the function y = -tcos(t) - t:
y(pi) = -(pi)cos(pi) - pi
= -(-pi) - pi
= 0
Since y(pi) = 0, the initial condition is satisfied as well.
Therefore, the function y = -tcos(t) - t is indeed a solution of the initial-value problem t(dy/dt) = y + t^2sin(t), y(pi) = 0.
Learn more about identity here:
https://brainly.com/question/1180838
#SPJ11
In 20P9, how many choices are there for the second batter if the total number on the team is 20?
(
Only 9 players will be in the lineup.)
A. 19
B. 20
C. 18
Answers
Answer:
the answer will be C
ik this bc I did the math
Someone please answer this I’m confused

Answers
1.
solve the
following
simultaneous equations graphically.
y = 8-x
y=x-2
Answers
Answer:
(5,3)
Step-by-step explanation:
Well to solve the following,
y = 8 - x
y = x - 2
Graphically.
We need to graph both equations,
Look at the image below ↓
By looking at the graph we can tell the intercept point is at (5,3).
Thus,
the solution is (5,3).
Hope this helps :)

Help pls I don’t remember how to do this so how do u find x, y, and z in this

Answers
Answer: 3) x = 87°; y = 93°; z = 63°
Step-by-step explanation:
x + 33 + 60 = 180 since they form a triangle.
x + 93 = 180
Subtract 93 from both sides
x = 87°
x and y are linear pairs so they're supplementary.
y + x = 180
y + 87 = 180
Subtract 87 from both sides
y = 93°
z + y + 24 = 180 since they also form a triangle
z + 93 + 24 = 180
z + 117 = 180
Subtract 117 from both sides
z = 63°
Hope this helped!
Oh and nannara nanke demo ii yo, ikasete yaru kara. :p
The velocity v, in feet per second, of the water pouring out of a small hole in the bottom of a cylindrical tank is given by v = 64h + 10 , where h is the height, in feet, of the water in the tank. What is the height of the water in the tank when the velocity of the water leaving the tank is 11 ft/s? Round to the nearest tenth.
Answers
The velocity v, in feet per second, of the water pouring out of a small hole in the bottom of a cylindrical tank is given by v = 64h + 10, where h is the height, in feet, of the water in the tank.
The height of the water in the tank when the velocity of the water leaving the tank is 11 ft/s is approximately equal to 0.2 feet.
How to find the height of the water in the tank?
Let's use the formula given: v = 64h + 10
To find the height h when the velocity v is given,
substitute v = 11ft/s and solve for h.11 = 64h + 10 ⇒ 64h = 11 - 10 = 1h = 1/64 feet = 0.015625 feet ≈ 0.02 feet (rounded to the nearest hundredth)
Therefore, the height of the water in the tank when the velocity of the water leaving the tank is 11 ft/s is approximately equal to 0.2 feet (rounded to the nearest tenth).
To know more about velocity visit:
https://brainly.com/question/29767936
#SPJ11
Use the graph to write a linear function that relates y to x

Answers
The linear function of the graph is written as: y = 4/3x + 2.
How to Write a Linear Function that Relates y to x of a Graph?The most common form of a linear function is y = mx + b, where m is the slope of the line and b is the y-intercept.
To write a linear function in this form, you will need to find the slope and y-intercept of the line.
The slope is the ratio of the change in y to the change in x, and the y-intercept is the point at which the line crosses the y-axis. Once you have these two values, you can substitute them into the equation and write the linear function.
Using the given graph:
Slope (m) = rise/run = 8/6
Slope (m) = 4/3
The y-intercept (b) = 2.
To write the linear function, substitute m = 4/3 and b = 2 into y = mx + b:
y = 4/3x + 2
Learn more about the linear function on:
https://brainly.com/question/15602982
#SPJ1
What is the value of this expression?
14 + 6 x (9-6)
Plz helppp
Answers
Answer:
32
Step-by-step explanation:
9-6 = 3
3 x 6 = 18
18 + 14 = 32
The circumference of the inner circle is 44 ft. The distance between the inner circle and the outer circle is 2 ft. By how many feet is the circumference of outer circle greater than the circumference of the inner circle? Use 22 over 7 for Pi (π.)
will give brainliest thingy to whomever answers this question corect first
Answers
The circumference of the outer circle is greater than the circumference of the inner circle by 44/7 feet.
What exactly is a circle?
A circle is a basic closed form made up of all points on a plane that are at a fixed distance from the centre. The radius is the distance between the centre and any point on the circle. A circle is often represented by the mathematical symbol "∘" or the equation (x-a)² + (y-b)² = r², where (a,b) is the center and r is the radius.
Now,
To find the circumference of the outer circle, we need to add the distance between the two circles to the circumference of the inner circle and then calculate the circumference of the resulting larger circle.
Circumference of the inner circle = πd = π*44 = 44π feet
Distance between the circles = 2 ft
Diameter of the larger circle = diameter of inner circle + distance between the circles = 44 ft + 2 ft = 46 ft
Circumference of the larger circle = πd = π(46) = 46π ft
Therefore, the circumference of the outer circle is greater than the circumference of the inner circle
by 46π - 44π
= 2*π feet=
=2*22/7=
=44/7 feet.
To know more about circle visit the link
brainly.com/question/11833983
#SPJ1
Which table made this graph?

Answers
Answer:
III
Step-by-step explanation:
Number 3 did. The contains the (-1,1) and (5,-2)
Answer:
lll
Step-by-step explanation:
its the number 3 so A
Kate places greeting cards from two different companies on a display rack that can hold up to 90 cards. She
has agreed to display at least 40 of company a's cards on the rack and at least 25 of company b's cards.
kate makes a profit of $0. 30 on each card she sells from company a and $0. 32 on each card she sells from
company b.
Answers
To get the maximum profit, Kate should display as many cards from company B as possible, since she makes a higher profit from those cards.
Let x be the number of cards from company A and y be the number of cards from company B.
The constraints are:
x + y ≤ 90 (the display rack can hold up to 90 cards) x ≥ 40 (at least 40 of company A's cards must be displayed) y ≥ 25 (at least 25 of company B's cards must be displayed)The objective function is:
P = 0.30x + 0.32y (the profit from selling the cards)
To maximize the profit, we need to maximize the value of y. Since the display rack can hold up to 90 cards, we can set y = 90 - x.
Substituting this into the objective function:
P = 0.30x + 0.32(90 - x)
P = 0.30x + 28.8 - 0.32x
P = -0.02x + 28.8
To maximize P, we need to minimize x. Since x must be at least 40, we can set x = 40.
Substituting this back into the objective function:
P = -0.02(40) + 28.8
P = 28
So the maximum profit Kate can make is $28, by displaying 40 cards from company A and 50 cards from company B.
Learn more about profit margin at https://brainly.com/question/28180283
#SPJ11
30% as a decimal round to the thousands place
Answers
Answer:
Your answer is 0.300 rounded to the thousands place.
Step-by-step explanation:
Hope this helps!
The volume of a sphere is decreasing at a constant rate of 23 cubic centimeters per
second. At the instant when the volume of the sphere is 7 cubic centimeters, what is
the rate of change of the radius? The volume of a sphere can be found with the
equation V 28. Round your answer to three decimal places.
Answers
The rate of change of the radius is 1.32cm²/s
The formula for calculating the volume of a sphere is expressed as:
\(v = \frac{4}{3} \pi r^3\)The rate of change of the volume is given as:
\(\frac{dv}{dt} = \frac{dv}{dr} \cdot \frac{dr}{dt} \\\frac{dv}{dt} = =4 \pi r^2 \cdot \frac{dr}{dt} \\\)Given the following paramters;
dv/dt = 23cm³/s
Volume = 7cm³
Get the radius of the sphere:
7 = 4/3 πr³\
21 = 4πr³
r³ = 21/4π
r = 1.18 cm
Get the rate of change of the radius to have:
\(23 = 4(3.14)(1.18)^2 \frac{dr}{dt} \\23 = 17.48 \frac{dr}{dt} \\\frac{dr}{dt}=1.32cm^2/s\)
Hence the rate of change of the radius is 1.32cm²/s
Learn more on volume of a sphere here: https://brainly.com/question/22807400
Analyze the diagram below and complete the instructions that follow.
Find the value of x.
A. 18
B. 22
C. 24
D. 28
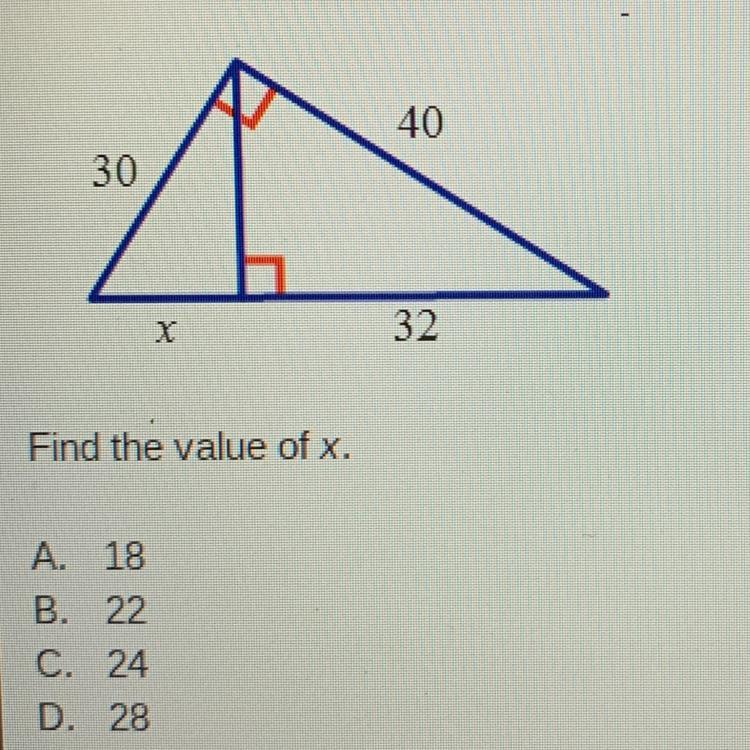
Answers
Answer:
A
Step-by-step explanation:
Using Pythagoras' identity on the large right triangle.
The square on the hypotenuse is equal to the sum of the squares on the other 2 sides, that is
(x + 32)² = 30² + 40² = 900 + 1600 = 2500 ( take the square root of both sides)
x + 32 =\(\sqrt{2500}\) = 50 ( subtract 32 from both sides )
x = 18 → A
Robert is pouring wax into cylindrical candle containers. Approximately 226.19 cubic inches of wax fill one candle jar. Which image represents that volume?
A cylinder with height 8 inches and radius 3 inches.
A cylinder with height 5 inches and radius 4 inches.
A cylinder with height 10 inches and radius 2 inches.
A cylinder with height 5 inches and radius 5 inches.
Answers
Answer:
The first choice.
Step-by-step explanation:
The volume must be about 226.19 in^3.
Volume of a cylinder = area of base * height4
= πr^2h = 226.19
r^2 = 226.19 / πh.
Consider the first of the choices:-
When h = 8 , r^2 = 226.19 /8π = 8.9998
So r = 3.00 to nearest hundredth.
So this is the required image.
Answer: It a
Step-by-step explanation:
Pls help I’m getting confused even though should be pretty easy.

Answers
Answer:
V = 108
Step-by-step explanation:
B = 9 x 4 = 36 Height of Triangular prism is 3 so 36 x 3 = 108
5. Let S {3³ + 2x + 1₁x³ + x, r = -5,³ + 10). Use the + 1 - Test Method to test whether S is linearly Linear Independence independent or not. (8 points) 6. Show that B= {[2, 1, 0, 0], [0, 1, 1,-1], [0,-1, 2, -2], [3, 1,0, -2]} is a basis for R¹. (8 points)
Answers
the set S = {3³ + 2x + 1₁x³ + x, r = -5,³ + 10} is linearly dependent.
B = {[2, 1, 0, 0], [0, 1, 1, -1], [0, -1, 2, -2], [3, 1, 0, -2]} is a basis for R¹.
To test whether the set S = {3³ + 2x + 1₁x³ + x, r = -5,³ + 10} is linearly independent or not, we can use the +1-Test Method. This method involves substituting random values (typically 0 and 1) into the polynomials and checking if the resulting vectors are linearly independent.
Let's substitute 0 and 1 into the given polynomials:
For x = 0:
3³ + 2(0) + 1₁(0)³ + 0 = 3³ = 27
-5³ + 10 = -125 + 10 = -115
For x = 1:
3³ + 2(1) + 1₁(1)³ + 1 = 3³ + 2 + 1₁ + 1 = 27 + 2 + 1 + 1 = 31
-5³ + 10 = -125 + 10 = -115
Now we have two vectors:
v1 = [27, -115]
v2 = [31, -115]
To test for linear independence, we need to see if there exist scalars c1 and c2, not both zero, such that c1 * v1 + c2 * v2 = 0. This can be done by setting up and solving a system of equations.
Let's set up the system of equations:
c1 * [27, -115] + c2 * [31, -115] = [0, 0]
This gives us two equations:
27c1 + 31c2 = 0 (Equation 1)
-115c1 - 115c2 = 0 (Equation 2)
We can solve this system of equations to determine the values of c1 and c2.
Multiplying Equation 1 by 115 and Equation 2 by 27, we get:
3105c1 + 3565c2 = 0 (Equation 3)
-3105c1 - 3105c2 = 0 (Equation 4)
Adding Equation 3 and Equation 4, we obtain:
0 = 0
Since the resulting equation is always true, this means that any values of c1 and c2 would satisfy the system of equations. In other words, there exist non-zero scalars c1 and c2 such that c1 * v1 + c2 * v2 = 0. Therefore, the vectors v1 and v2 are linearly dependent.
Hence, the set S = {3³ + 2x + 1₁x³ + x, r = -5,³ + 10} is linearly dependent.
Now let's show that the set B = {[2, 1, 0, 0], [0, 1, 1, -1], [0, -1, 2, -2], [3, 1, 0, -2]} is a basis for R¹ (the set of all real numbers).
To show that B is a basis, we need to demonstrate two properties:
B spans R¹: Every vector in R¹ can be expressed as a linear combination of vectors in B.
B is linearly independent: The vectors in B are linearly independent.
Spanning R¹:
Let's consider an arbitrary vector v = [a, b, c, d] in R¹, where a, b, c, and d are real numbers.
We need to show that v can be expressed as a linear combination of the vectors in B.
By multiplying the vectors in B by appropriate scalar coefficients and adding them, we have:
x₁ * [2, 1, 0, 0] + x₂ * [0, 1, 1, -1] + x₃ * [0, -1, 2, -2] + x₄ * [3, 1, 0, -2] = [a, b, c, d]
This leads to the following system of equations:
2x₁ + 0x₂ + 0x₃ + 3x₄ = a
x₁ + x₂ - x₃ + x₄ = b
x₂ + (-x₃) + 2x₃ + 0x₄ = c
-1x₂ - x₃ - 2x₃ - 2x₄ = d
Simplifying the system of equations, we have:
2x₁ + 3x₄ = a
x₁ + x₂ - x₃ + x₄ = b
2x₂ + 2x₃ = c
-1x₂ - 3x₃ - 2x₄ = d
This system of equations has a unique solution for every choice of a, b, c, and d. Therefore, any vector v in R¹ can be expressed as a linear combination of the vectors in B.
Linear Independence:
To show that the vectors in B are linearly independent, we need to demonstrate that the equation:
x₁ * [2, 1, 0, 0] + x₂ * [0, 1, 1, -1] + x₃ * [0, -1, 2, -2] + x₄ * [3, 1, 0, -2] = [0, 0, 0, 0]
only has the trivial solution, where x₁ = x₂ = x₃ = x₄ = 0.
We can rewrite the equation as a system of equations:
2x₁ + 0x₂ + 0x₃ + 3x₄ = 0
x₁ + x₂ - x₃ + x₄ = 0
0x₁ + x₂ + (-x₃) + 2x₃ = 0
0x₁ - x₂ - 2x₃ - 2x₄ = 0
Simplifying the system of equations, we have:
2x₁ + 3x₄ = 0
x₁ + x₂ - x₃ + x₄ = 0
x₂ - x₃ + 2x₃ = 0
-x₂ - 3x₃ - 2x₄ = 0
This system of equations has only the trivial solution x₁ = x₂ = x₃ = x₄ = 0. Therefore, the vectors in B are linearly independent.
Since B satisfies both properties of being a basis (spanning R¹ and linearly independent), we can conclude that B = {[2, 1, 0, 0], [0, 1, 1, -1], [0, -1, 2, -2], [3, 1, 0, -2]} is a basis for R¹.
Learn more about Linear independence here: brainly.com/question/30704555
#SPJ11
(11x+2)° (8x+7)° find value of x
Answers
Answer:
Rate = 56 gal / 7 min
= 8 gal / min
Step-by-step explanation:
Hope this helps leave a heart ad maybe brailiest
describe the apparent relationship between the two variables under consideration. choose the correct choice below. a. test score remains constant as the number of study hours increases. b. test score tends to decrease as the number of study hours increases. c. test score tends to increase as the number of study hours increases. d. there is no apparent relationship between study hours and test score.
Answers
Based on the given information, the question is asking about the apparent relationship between two variables: study hours and test score. The correct answer is c.
Test score tends to increase as the number of study hours increases. This suggests a positive correlation between the two variables, meaning that as one variable (study hours) increases, the other variable (test score) also tends to increase.
The apparent relationship between the two variables under consideration, which are study hours and test score, can be described as follows:
Your answer: c. Test score tends to increase as the number of study hours increases.
This is because, generally, the more time a person spends studying, the better their understanding of the material, which often leads to a higher test score.
Visit here to learn more about variables:
brainly.com/question/17344045
#SPJ11
Standard 8.EE.A.1 -
Which expression is equivalent to (3x^2)^4?
2 points
(a) 12x^8
(b) 12x^6
(c) 81x^6
(d) 81x^8
Answers
Question 2
Use the technique of Laplace transformation to solve the differential equation
d^2y/dx +y=0 dx
for the initial conditions
dy(0)/dx = 2, y(0) = 1
Answers
To use the Laplace transformation to solve the following differential equation, we will first apply the transformation to the problem and its initial conditions. F(s) denotes the Laplace transform of a function f(x) and is defined as: \(Lf(x) = F(s) = [0,] f(x)e(-sx)dx\)
When the Laplace transformation is applied to the given differential equation, we get:
\(Ld2y/dx2/dx2 + Ly = 0\) .
If we take the Laplace transform of each term, we get: \(s^2Y(s) = 0 - sy(0) - y'(0) + Y(s)\).
Dividing both sides by \((s^2 + 1),\), we obtain:
\(Y(s) = (s + 2) / (s^2 + 1)\).
Now, we can use the partial fraction decomposition to express Y(s) in terms of simpler fractions:
Y(s) = (s + 2) / (\(s^{2}\)+ 1) = A/(s - i) + B/(s + i) .
Multiplying through by (\(s^{2}\) + 1), we have:
s + 2 = A(s + i) + B(s - i).
Expanding and collecting like terms, we get:
s + 2 = (A + B)s + (Ai - Bi).
Comparing the coefficients of s on both sides, we have:
1 = A + B and 2 = Ai - Bi.
From the first equation, we can solve for B in terms of A:B = 1 - A Substituting B into the second equation, we have:
2 = Ai - (1 - A)i
2 = Ai - i + Ai
2 = 2Ai - i
From this equation, we can see that A = 1/2 and B = 1/2. Substituting the values of A and B back into the partial fraction decomposition, we have:
Y(s) = (1/2)/(s - i) + (1/2)/(s + i). Now, we can take the inverse Laplace transform of Y(s) to obtain the solution y(x) in the time domain. The inverse Laplace transform of 1/(s - i) is \(e^(ix).\)
As a result, the following is the solution to the given differential equation:\((1/2)e^(ix) + (1/2)e^(-ix) = y(x).\)
Simplifying even further, we get: y(x) = sin(x)
As a result, given the initial conditions dy(0)/dx = 2 and y(0) = 1, the solution to the above differential equation is y(x) = cos(x).
For more such questions on Laplace transformation , visit:
https://brainly.com/question/29583725
#SPJ8
11+6x=2x-13 show your work
Answers
Hope this helps!

Answer:
x=0.5
My previous answer got deleted
Step-by-step explanation:
11+6x=2x-13
11-11+6x=2x-13-11
6x=2x-24
6x-2x=2x-2x-24
4x=-24
x=-6
Which measurement is equivalent to 84 inches?
A.8 feet
B. 1 yard, 2 feet, 24 inches
C. 7 feet, 4 inches
D. 4 feet, 40 inches
Answers
Answer: A
Step-by-step explanation:
Answer: B. 1 yard, 2 feet, 24 inches
Step-by-step explanation: 1 yard is 36 inches. Each feet is 12 inches, but there are 2 feet so 12 times 2 is 24 inches. And the last is just 24 inches. So, 36 + 24 + 24 = 84 inches
a​ _______ variable is a variable that has a single numerical​ value, determined by​ chance, for each outcome of a procedure.
Answers
A random variable is a variable that has a single numerical value, determined by chance, for each outcome of a procedure.
A random variable is defined as a variable that has posses a single numerical value, and determined for each outcome of an event. That is a variable whose value is either unknown or a function that assigns values to each of an experiment's outcomes. It can be either discrete (having specific values) or continuous (any value in a continuous range). Generally, random variables are represented by capital letters for example, X and Y. For example consider the tossing of coin event, then the values Heads = 0 and Tails= 1 and we have a Random Variable "X". Hence, required answer is random variable.
For more information about random variable, visit :
https://brainly.com/question/14356285
#SPJ4
Complete question:
a _______ variable is a variable that has a single numerical value, determined bychance, for each outcome of a procedure.

when determining the pooled population variance estimate for a t test for independent means with unequal sample sizes,: group of answer choices the variance of both of the original populations must be known (as opposed to estimated) the scores from both samples are combined to form a single sample, and the estimated variance is figured in the usual way, but using this combined sample the estimates based on each of the samples are averaged in such a way as to give more influence to the estimate based on more participants the variance of at least one of the original populations must be known (as opposed to estimated), but the other can be estimated from sample scores
Answers
The estimates based on each of the samples are averaged in such a way as to give more influence to the estimate based on more participants.
What is population variance?
Each data point's distance from the population mean is quantified by the population variance, which is a measure of dispersion. The average of the squares of the deviations from the data's mean value is known as population variance.
Hence, when determining the pooled population variance estimate for a t test for independent means with unequal sample sizes, the estimates based on each of the samples are averaged in such a way as to give more influence to the estimate based on more participants.
To learn more about population variance from the given link:
https://brainly.com/question/25426624
#SPJ4
Can someone please help

Answers
Answer:
b. Complementary gas masks
Step-by-step explanation:
Adjacent means that the two angles are right next to each other and touching. The two angels in the photo are touching. Supplementary means that the two angels can for together to make a 180 degree line. The two angels in the photo make a 180 degree line. Complementary means that the two angels make a 90 degree angel. Since the two angels already make a 180 degree angels then, they cannot make a 90 degree angel. The question is asking for what it is not so, complements would be the answer.
7th grade math!! Please help this is the last question on my assignment and I’m so confused,

Answers
The area of the figure is 644 square inches.
Given,
Figure : triangle + 3 semicircles
We need to find the area of the figure.
What are the area of a triangle and a circle?Area of a circle: 1/2 x base x height
Area of a circle: \(\pi\)r²
Find the area of the triangle.
We have,
Base = 20 in
Height = 17.3 in
Area = 1/2 x base x height
= 1/2 x 20 x 17.3
= 1 x 10 x 17.3
= 173 square inches
Find the area of a circle
We have,
radius = 10 in
Area = \(\pi\) x 10²
= 3.14 x 100
= 314 square inches
Find the area of a semicircle
= area of circle / 2
= 314/2
= 157 square inches
Find the area of the figure
= area of the triangle + 3 x area of the semicircle
= 173 + 3 x 157
= 173 + 471
= 644 square inches.
Thus the area of the figure is 644 square inches.
Learn more about the area of combined figures here:
https://brainly.com/question/22964077
#SPJ1