La distancia de la Tierra a la Luna es de doscientos treinta y ocho mil novecientas millas. Escribe la distancia en forma estándar y forma expandida.
Answers
Answer: two hundred thirty-eight thousand nine, (2 x 100,000) + (30 x 10,000) + (8 x 1,000) + (9 x 1). doscientos treinta y ocho mil nueve, (2 x 100.000) + (30 x 10.000) + (8 x 1.000) + (9 x 1).
Step-by-step explanation: I learned it already.
Related Questions
Matt's pool table is 3 feet wide and 9 feet long. Matt wants to replace the felt on the pool table. The felt costs $4.00 per square foot. How much would it cost in total to replace the felt on the pool table?
Answers
Answer:
$108
Step-by-step explanation:
3X9= 27square foot. Then you multiply 27 by 4, which equals $108
A company sells widgets. The amount of profit, y, made by the company, is the selling price of each widget, x, by the given equation. Using this equation, find out what price the widgets should be sold for, to the nearest cent, for the company to make the maximum profit. y = -x^2+ 101x – 900
Answers
We want maximum profit, which is the max value of y.
We basically want for which x value, we have y as the maximum.
First,
let's take the derivative of y:
\(\begin{gathered} y=-x^2+101x-900 \\ y^{\prime}=-2x+101 \end{gathered}\)Maximum is when the derivative is equal to 0. So, the x-value when derivative is 0:
\(\begin{gathered} y^{\prime}=-2x+101 \\ 0=-2x+101 \\ 2x=101 \\ x=\frac{101}{2} \\ x=50.5 \end{gathered}\)To get max profit, the widgets should be sold at $50.50
20. SAILING On a sailing trip, each passenger needs a
life jacket, a lunch, and a bottle of water. Write an
expression in simplest form that represents the
weight carried by r passengers on the sailing trip.
Interpret the expression.
Answers
How do you estimate a scatter plot?
Answers
Answer:
Step-by-step explanation:
1.Collect pairs of data where a relationship is suspected.
2.Draw a graph with the independent variable on the horizontal axis and the dependent variable on the vertical axis. ...
3.Look at the pattern of points to see if a relationship is obvious. ...
4.Divide points on the graph into four quadrants.
where in the world would you expect to have a relative humidity of close to 100%? what about close to 0%?
Answers
100% humidity is very common in many coastal zones, near rivers or lakes or in your bathroom when you take a shower, and possibly in Alaska as well as UAE.
Relative humidity:
Relative humidity is the ratio of the current absolute humidity to the highest possible absolute humidity (which depends on the current air temperature). A reading of 100 % relative humidity means that the air is totally saturated with water vapor and cannot hold any more, creating the possibility of rain. This doesn't mean that the relative humidity must be 100 percent in order for it to rain — it must be 100 percent where the clouds are forming, but the relative humidity near the ground could be much less.
0% humidity means there is an absence of water vapor in the air.
To learn more about Relative humidity visit:
https://brainly.com/question/22069910
#SPJ4
6)
5ft
3ft.
14ft
8 ft
I need the surface area someone help me
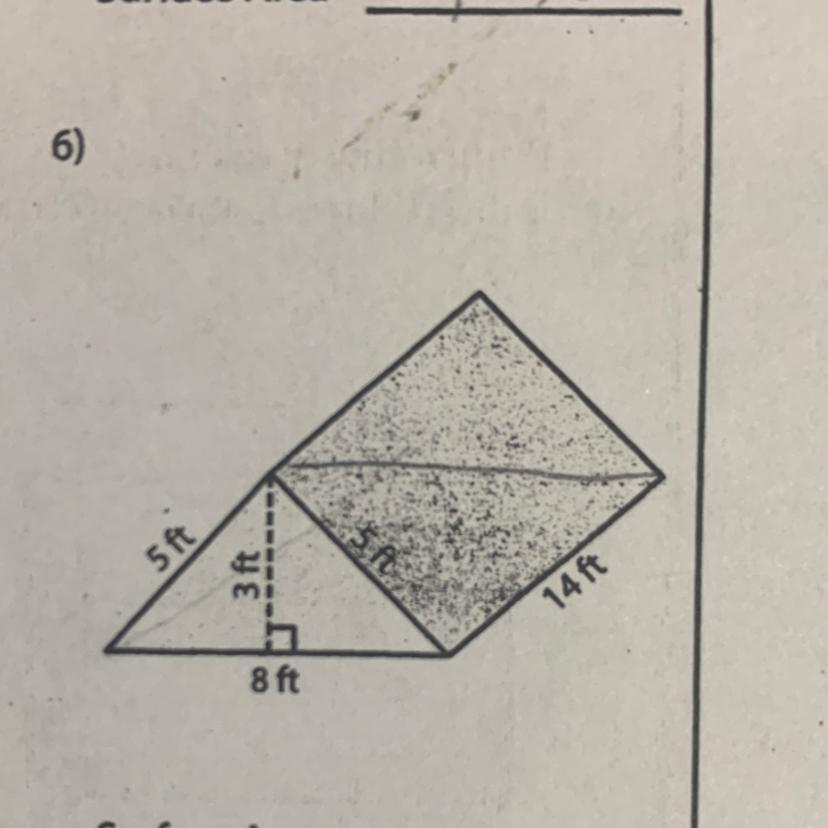
Answers
Answer:
258ft squared is possibly the answer

If x = 3 and y = 27, evaluate the following expression:
х/y
Give your answer as a fraction in its simplest form.
Answers
Step-by-step explanation:
given expression → x/y
we know,
x = 3 and y = 27
according to expression
3/27 → 1/9
therefore 1/9 is the answer.
Hope this answer helps you!
Answer:
1/9
Step-by-step explanation:
1. First, let's plug in the values of x and y.
\(\frac{x}{y}\) \(\frac{3}{27}\)2. Next, we have to simplify and find the greatest common factor between 3 and 27.
Factors of 3: 1, 3Factors of 27: 1, 3, 9, 273. As you can see, 3 is the GCF of 3 and 27, so we divide both 3 and 27 by 3.
\(\frac{3/3}{27/3}\) \(\frac{1}{9}\)Therefore, the answer is 1/9!
Have a lovely rest of your day/night, and good luck with your assignments! ♡
Please help due ASAP
Show workings

Answers
Answer:
CD=66
Step-by-step explanation:
12x-30=6x+18
6x=48
x=8
12(8)-30=66
CD=66
Here is an equation that is true for all values of x: 6(x + 3) = 6x + 18. Londyn saw this equation and says she can tell 18( x + 3) + 32 = 3(6x + 18) + 32 is also true for any value of x. How can she tell? Explain your reasoning.

Answers
We need to decide whether the given equations are always or never true for values of x .The given equations are ,
\(x - 12 = x + 1\)solve out for x,
\(\longrightarrow x -x =12+1\\ \)
\(\longrightarrow 0 =13\\ \)
This can never be true. Hence the equation is never true for any values of x.
\(x + \frac{3}{4} = x - \frac{3}{4} \)solve out for x,
\(\longrightarrow x -x =\dfrac{3}{4}+\dfrac{3}{4}\\ \)
\(\longrightarrow 0=\dfrac{3}{2}\)
This can never be true. hence the equation is never true for any values of x.
\(4(x + 3) = 8x + 12 - 4x\)solve out for x,
\(\longrightarrow 4x +12=8x+12-4x\\\)
\(\longrightarrow 4x -8x +4x =12-12\\\)
\(\longrightarrow 0=0\)
hence this equation is true for all values of x.
\(2x - 8 - x = x - 8\)solve out for x,
\(\longrightarrow 2x -x -x =8+8\\ \)
\(\longrightarrow 0=0 \)
hence the equation is true for all values of x.
\(2(x + 5) + 3x = 5(x - 5)\)solve out for x,
\(\longrightarrow 2x +10+3x =5x-25\\ \)
\(\longrightarrow 5x -5x =-25-10\\\)
\(\longrightarrow 0 =-35\)
This can never be true. hence the equation is never true for any values of x.
and we are done!
can someone answer this ITS DUE TOMORROW
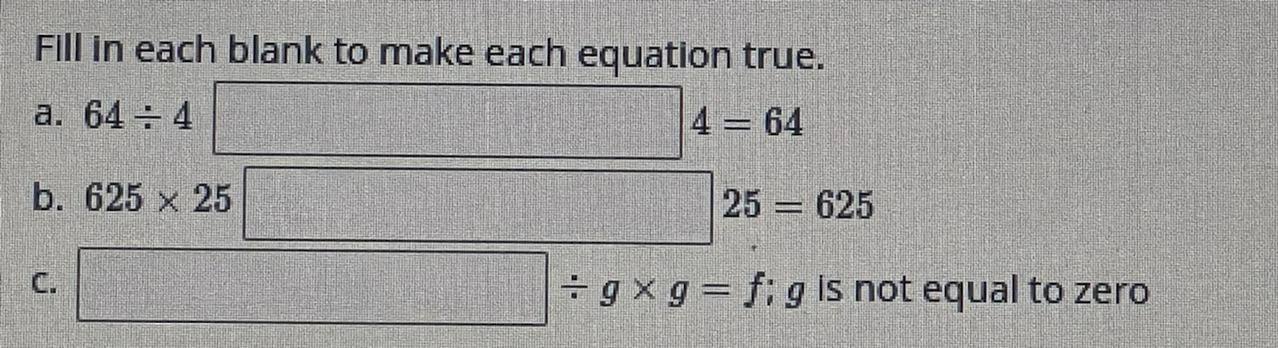
Answers
Answer:
a-x
b-/
Step-by-step explanation:
64/4x4=64
625x25/25=625
Help me and show your work.

Answers
Answer:
y = 4x + 5
Step-by-step explanation:
The equation of a straight line line is;
y = mx + b
where m is the slope and b is the y-intercept
We start by calculating the slope value by using the slope equation
m = (y2-y1)/(x2-x1)
m = (9+ 7)/(1+ 3) = 16/4 = 4
So we have the equation as;
y = 4x + b
to get the value of b, we substitute the coordinates of any of the two points
let us use (1,9)
9 = 4(1) + b
b = 9-4
b = 5
so, we have the equation of the line as;
y = 4x + 5
Can someone help me please



Answers
Step-by-step explanation:
you can follow the same procedure for others


a correlation measures the relationship between two variables, x and y. the relationship is described by what three characteristics? please describe these 3 characteristics
Answers
A correlation measures the strength, direction, and form of the relationship between two variables, x and y. The strength of the relationship refers to how closely the variables are related, with values ranging from -1 to 1.
A value of -1 indicates a perfect negative correlation, meaning that as one variable increases, the other decreases. A value of 1 indicates a perfect positive correlation, meaning that as one variable increases, the other also increases. A value of 0 indicates no correlation, meaning that the variables are not related.
The direction of the relationship refers to whether the variables move in the same direction or opposite directions. A positive correlation indicates that the variables move in the same direction, meaning that as one variable increases, so does the other.
A negative correlation indicates that the variables move in opposite directions, meaning that as one variable increases, the other decreases.
The form of the relationship refers to the pattern of the relationship between the variables. The form can be linear, meaning that the relationship between the variables can be described by a straight line, or nonlinear, meaning that the relationship between the variables cannot be described by a straight line.
Nonlinear relationships can take various forms, such as quadratic, logarithmic, or exponential. The form of the relationship can have important implications for interpreting the correlation coefficient and making predictions based on the relationship between the variables.
To learn more about correlation click here:
brainly.com/question/29985055
#SPJ11
Question 11 (Multiple Choice Worth 2 points)
(Scale Factor MC)
An engineer has a 60:1 scale drawing of a bridge. The dimensions of the scaled bridge deck are 48 inches by 4 inches. What is
the area of the actual bridge deck in square feet?
O5,280 square feet
O2,640 square feet
288 square feet
O240 square feet
2
Answers
Answer:
4800 ft²
or
5280 ft²
Step-by-step explanation:
The deck is 48 inches by 4 inches in the drawing.
The scale is 60:1, so the real dimensions are 60 times greater than the drawing dimensions.
Let's calculate the real dimensions and also convert to feet from inches.
length = 48 in. × 60 × (1 ft)/(12 in.) = 240 ft
width = 4 in. × 60 × (1 ft)/(12 in.) = 20 ft
The real dimensions of the deck are 240 ft by 20 ft.
area = length × width
area = 240 ft × 20 ft = 4800 ft²
If the correct drawing width is really 4 2/5 in., then the real area is:
48 in. × 4 2/5 in. × 60 × 60 / 144 ft²/in.² = 5280 ft²
what is 2 1/2 divided by 1 5/8
Answers
Answer:
2 1/2 divided by 1 5/8 equals to 1.53846153846
The transformation shown is a
.
The measure of A is
the measure of A’.
Side AB is
side A’B’.
Answers
Answer:
no photooooooooooooooooooooooooooooo
Answer:
no photttttoooooooo
Step-by-step explanation:
Question 4 (25 pts.) If p is an odd prime, then prove that 1².3²... (p-2)² = (-1) (mod p)
Answers
As we have proved that if p is an odd prime, then the product 1² · 3² · ... · (p-2)² is congruent to -1 modulo p.
To prove the statement, let's consider the product P = 1² · 3² · ... · (p-2)². Our goal is to show that P ≡ -1 (mod p), which means P leaves a remainder of -1 when divided by p.
First, we note that p is an odd prime. This means that p can be expressed as p = 2k + 1, where k is an integer. We can rewrite P using this representation:
P = (1 · 1) · (3 · 3) · ... · ((2k - 1) · (2k - 1)).
Now, let's examine P more closely. We can write each factor in P as:
(2i - 1) · (2k - (2i - 1)).
Expanding this expression, we get:
(2i - 1) · (2k - 2i + 1) = 4ik - 2i + 2ki - k - 2i + 1 = 4ik - 4i + 2ki - k + 1.
We can simplify this further as:
(4ik - 4i + 2ki - k + 1) = (4ik - 4i) + (2ki - k + 1) = 4i(k - 1) + k(2i - 1) + 1.
Now, let's consider the expression (2i - 1) modulo p. Since p = 2k + 1, we can rewrite (2i - 1) as:
(2i - 1) ≡ 2i - 1 (mod p).
Substituting this back into our expression for P, we have:
P ≡ (4i(k - 1) + k(2i - 1) + 1) (mod p).
Now, let's consider the sum (4i(k - 1) + k(2i - 1)) modulo p. We can write this as:
(4i(k - 1) + k(2i - 1)) ≡ 4ik - 4i + 2ki - k ≡ -3i + k(i - 1) (mod p).
Since p = 2k + 1, we have -3i + k(i - 1) ≡ -3i + (p - 1)(i - 1) (mod p).
Expanding (p - 1)(i - 1), we get:
-3i + (p - 1)(i - 1) = -3i + pi - p - i + 1 = -4i - p + pi + 1.
Now, let's consider the expression (-4i - p + pi + 1) modulo p. We can rewrite this as:
(-4i - p + pi + 1) ≡ -4i - p (mod p).
Since -p ≡ 0 (mod p), we have -4i - p ≡ -4i (mod p).
Therefore, we have shown that:
P ≡ -4i (mod p).
Now, let's consider the range of i. We know that i takes on values from 1 to (p - 2)/2, inclusive. Since p is an odd prime, (p - 2)/2 is an integer. Therefore, we can rewrite P as:
P ≡ -4(1 + 2 + 3 + ... + [(p - 2)/2]) (mod p).
The sum 1 + 2 + 3 + ... + n can be expressed as n(n + 1)/2. Substituting this into our expression for P, we get:
P ≡ -2[(p - 2)/2] [(p - 2)/2 + 1] (mod p).
Simplifying further, we have:
P ≡ -[(p - 2)/2] [(p - 2)/2 + 1] (mod p).
Since p is an odd prime, we can rewrite p - 2 as 2k - 1. Substituting this into our expression, we get:
P ≡ -[k] [k + 1] (mod p).
Now, let's expand the product [k] [k + 1]:
[k] [k + 1] = k² + k.
Substituting this back into our expression for P, we have:
P ≡ -(k² + k) (mod p).
Now, recall that p = 2k + 1. Substituting this into our expression, we get:
P ≡ -(k² + k) ≡ -(k² + k + 1) + 1 ≡ -(k² + 2k + 1) + 1 ≡ -[(k + 1)²] + 1 (mod p).
Since p = 2k + 1, we have (k + 1)² ≡ -1 (mod p). Substituting this back into our expression, we finally have:
P ≡ -[(k + 1)²] + 1 ≡ -1 + 1 ≡ 0 ≡ -1 (mod p).
To know more about prime here
https://brainly.com/question/30646191
#SPJ4
The radius of a circle is 12 m what is the area
Answers
Answer:
The area is 452.3
Step-by-step explanation:
A= 3.14r2
A= 3.14 times 12~2
A= 452.2
For the floating point bumber systems showed that (b, s, m, M)=(10, 4, -99, 99), what are the values of
(f) the floating representation of 1.0 in this system
(g) the largest number that is less than 1.0
(h) the gap length to the left of 1.0
(i) the smallest number greater than 1.0
(j) the gap length to the right of 1.0 (k) the ratio of (the gap length to the right of 1.0) to (the gap length to the left of 1.0)
(l) the smallest positive integer that cannot be represented in this system
(m) the smallest representable integer that is greater than the smallest nonrepresentable positive integer, if any such exists
(n) the length of the gap in which the smallest nonrepresentable integer lies, if any such exists
(o) the number of nonrepresentable integers, if any, in the gap in part (n)
(p) the largest number
(q) the gap length to the left of the largest number
(r) the number of nonrepresentable integers, if any, in the gap immediately to the left of the largest number
Answers
Given the floating-point number system (b, s, m, M) = (10, 4, -99, 99), let's find the values of the given expressions:
(f) The floating representation of 1.0 in this system:
The floating-point representation of 1.0 in this system is 1.000 × 10^0.
(g) The largest number that is less than 1.0:
The largest number that is less than 1.0 in this system is 0.9999 × 10^0.
(h) The gap length to the left of 1.0:
The gap length to the left of 1.0 in this system is 0.0001 × 10^0.
(i) The smallest number greater than 1.0:
The smallest number greater than 1.0 in this system is 1.0001 × 10^0.
(j) The gap length to the right of 1.0:
The gap length to the right of 1.0 in this system is 0.0001 × 10^0.
(k) The ratio of (the gap length to the right of 1.0) to (the gap length to the left of 1.0):
The ratio of the gap length to the right of 1.0 to the gap length to the left of 1.0 is 1.
(l) The smallest positive integer that cannot be represented in this system:
In this system, the smallest positive integer that cannot be represented is 10000 (10^4), which is outside the specified range.
(m) The smallest representable integer that is greater than the smallest nonrepresentable positive integer:
Since the smallest nonrepresentable positive integer is 10000 (10^4), the smallest representable integer greater than that is 10001 (10^4 + 1).
(n) The length of the gap in which the smallest nonrepresentable integer lies:
The length of the gap in which the smallest nonrepresentable integer lies is 1.
(o) The number of nonrepresentable integers in the gap in part (n):
In this case, there is only one nonrepresentable integer, which is the smallest nonrepresentable integer itself.
(p) The largest number:
The largest number in this system is 0.9999 × 10^99.
(q) The gap length to the left of the largest number:
The gap length to the left of the largest number is 0.0001 × 10^99.
(r) The number of non representable integers in the gap immediately to the left of the largest number:
Since the range specified for this system does not include any non representable integers, the number of non representable integers in the gap is zero.
Learn more about floating point here:
https://brainly.com/question/31691346
#SPJ11
Josie had 12 beads on her necklace. Then she added b more beads. Write an expression that shows how many beads are on the necklace in all. please write a expression like b-12 or b+?
Answers
The expression that shows how many beads are on the necklace in all is:
b + 12.
What is expression?An expression in mathematics is a combination of numbers, variables, and/or operators that represents a mathematical relationship or quantity. It may contain constants, variables, coefficients, and mathematical operations such as addition, subtraction, multiplication, division, and exponentiation. Expressions are often used to describe or represent real-world situations, and can be simplified, evaluated, or manipulated using algebraic rules and properties.
In the given question,
To write an expression that shows how many beads are on Josie's necklace in all after adding b more beads:
Start with the initial number of beads on the necklace, which is 12.
To this, add the number of beads Josie added, which is b.
Combine the two terms to form the final expression: 12 + b.
Therefore, the expression that shows how many beads are on Josie's necklace in all after adding b more beads is 12 + b.
To know more about expressions and equations, visit:
https://brainly.com/question/11537309
#SPJ1
Assume y≠60 which expression is equivalent to (7sqrtx2)/(5sqrty3)

Answers
Answer:
The equivalent will be:
\(\frac{\sqrt[7]{x^2}}{\sqrt[5]{y^3}}=\left(\:x^{\frac{2}{7}}\right)\left(y^{-\frac{3}{5}}\right)\)
Therefore, option 'a' is true.
Step-by-step explanation:
Given the expression
\(\frac{\sqrt[7]{x^2}}{\sqrt[5]{y^3}}\)
Let us solve the expression step by step to get the equivalent
\(\frac{\sqrt[7]{x^2}}{\sqrt[5]{y^3}}\)
as
\(\sqrt[7]{x^2}=\left(x^2\right)^{\frac{1}{7}}\) ∵ \(\mathrm{Apply\:radical\:rule}:\quad \sqrt[n]{a}=a^{\frac{1}{n}}\)
\(\mathrm{Apply\:exponent\:rule:\:}\left(a^b\right)^c=a^{bc},\:\quad \mathrm{\:assuming\:}a\ge 0\)
\(=x^{2\cdot \frac{1}{7}}\)
\(=x^{\frac{2}{7}}\)
also
\(\sqrt[5]{y^3}=\left(y^3\right)^{\frac{1}{5}}\) ∵ \(\mathrm{Apply\:radical\:rule}:\quad \sqrt[n]{a}=a^{\frac{1}{n}}\)
\(\mathrm{Apply\:exponent\:rule:\:}\left(a^b\right)^c=a^{bc},\:\quad \mathrm{\:assuming\:}a\ge 0\)
\(=y^{3\cdot \frac{1}{5}}\)
\(=y^{\frac{3}{5}}\)
so the expression becomes
\(\frac{x^{\frac{2}{7}}}{y^{\frac{3}{5}}}\)
\(\mathrm{Apply\:exponent\:rule}:\quad \:a^{-b}=\frac{1}{a^b}\)
\(=\left(\:x^{\frac{2}{7}}\right)\left(y^{-\frac{3}{5}}\right)\) ∵ \(\:\frac{1}{y^{\frac{3}{5}}}=y^{-\frac{3}{5}}\)
Thus, the equivalent will be:
\(\frac{\sqrt[7]{x^2}}{\sqrt[5]{y^3}}=\left(\:x^{\frac{2}{7}}\right)\left(y^{-\frac{3}{5}}\right)\)
Therefore, option 'a' is true.
dolor sit amet, consectetuer adipiscing elit. Aenean commodo ligula eget
Answers
100 is the answerrrrrrrrrrrrrrrrrrr
f(x)=3x²-x+2
find f (-4)
Answers
48=3ײ-4
(4-)-2=6
48+6=54
What is the volume of a cube with a side length of 5/6 cm?
Answers
Answer:
.58 cm^3
Step-by-step explanation:
The formula for finding the volume of a cube is V = a^3 where a is a side length.
If you input the given value into the formula, you get .58 cm^3
Please mark as brainliest ;)
PLZ I NEED THIS ASAP!! ILL GIVE YOU BRAINLIST!!!

Answers
What current density would produce the vector potential, A = k Î¦Ë (where k is a constant), in cylindrical coordinates?
Answers
The current density vector Jz that would produce the given vector potential A in cylindrical coordinates is Jz = -k/c r sin(θ).
The current density required to produce the given vector potential A = kΦ is J_φ = k (∂Φ/∂ρ), where Φ is the magnetic flux.
First, let's define the cylindrical coordinates:
r = r(theta, z)
θ = θ(theta, z)
z = z
Now, we need to find the vector potential A = k Φ. Using the right-hand rule, we can determine the direction of the vector potential as the direction of the positive z-axis.
The curl of A in cylindrical coordinates is given by:
curl(A) = (1/r)(∂/∂r)(rA) + (1/rsin(θ))(∂/∂θ)(Asin(θ)) + (1/sin(θ))(∂/∂z)(Acos(θ))
Since we want A = k Φ, we have kA = -1/r(∂A/∂r) - 1/rsin(θ)(∂A/∂θ) - 1/sin(θ)(∂A/∂z).
Substituting the expression for A, we get:
k(1/r)(∂A/∂r) - 1/rsin(θ)(∂A/∂θ) - 1/sin(θ)(∂A/∂z) = -1
Now, we need to find the divergence of the magnetic field B, which is given by:
div(B) = (1/r)(∂B/∂r) + (1/rsin(θ))(∂B/∂θ) + (1/sin(θ))(∂B/∂z)
Using the Biot-Savart law, we can find the magnetic field B in cylindrical coordinates. The magnetic field is given by:
B = (1/4π)∫(J(r',θ',z') x r') x r dA'
where J(r',θ',z') is the current density vector.
We can substitute the expression for J in cylindrical coordinates and simplify the integral to obtain:
B = (1/4π)∫[(-1/r)(∫z' J(r',θ') dθ')r') - (1/sin(θ'))(∫z' J(r',θ') dz')] x r dA'
Now, we need to find the current density vector J. Using the Maxwell-Ampere law, we can find the curl of the electric field E in vacuum, which is given by:
curl(E) = -∂B/∂t
Substituting the expression for E in cylindrical coordinates, we get:
curl(E) = -∂B/∂t = (1/c) ∂(Jz)/∂t
where c is the speed of light in vacuum.
Now, we can substitute these expressions for B and curl(E) into the equation for the magnetic field and simplify to obtain:
k(1/r)(∂A/∂r) - 1/rsin(θ)(∂A/∂θ) - 1/sin(θ)(∂A/∂z) = -1
(1/c)(∂(Jz)/∂t) - 1/rsin(θ)(∂A/∂θ) - 1/sin(θ)(∂A/∂z) = -1
Solving these two equations simultaneously, we can find the constants k and Jz. Once we have these values, we can substitute them into the expression for the vector potential A to obtain:
A = k r sin(θ) + Jz/c
Therefore, the current density vector Jz that would produce the given vector potential A in cylindrical coordinates is Jz = -k/c r sin(θ).
Learn more about current density
https://brainly.com/question/31785329
#SPJ4
Determine if the given lines are parallel, perpendicular, or neither
19. y + 5 = -12
x-y=10
20. 3x-5y=10
10x+6y=-36
I WILL GIVE BRAINEST!!! I NEED HELP DUE IN 2 HOURS
19 AND 20!!
I WILL ONLY GIVE BRAINEST IF YOU ACTUALLY DO THAT PROBABLY

Answers
Answer:
i had to do this like a few weeks ago but i only remember that the parallel ones have the same slope
Step-by-step explanation:
Step-by-step explanation:
19.y+5=-12
y=-12-5
y=-17
x-y=10
x+17=10
x=10-17
x=-7
20.3x-5y=10
3*-7-5*-17=10
-21+85=10
64=10
10x+6y=-36
10*-7+6*-17=-36
-70+102=-36
32=-36
Find the derivative of the function. y = arctan √[(1 − x) /(1 + x)]
y' = ?
and
Find the derivative of the function. y = 3tan−1 [x − √(1 + x^2)]
y' = ?
Answers
The derivative function for equations 1 and 2 will be
y' = -1/ [2√(1-x²)] and y' = 3/[2(1 + x²)] respectively
Here we need to find the derivative of
\(y = tan^{-1}\sqrt{\frac{1-x}{1+x} }\)
Let x = cos2z
Hence we get
\(y = tan^{-1}\sqrt{\frac{1-cos2z}{1+cos2z} }\)
\(or, y = tan^{-1}\sqrt{\frac{2sin^{2}z}{2cos^{2}z} }\)
\(or, y = tan^{-1}(tanz)\)
or, y = z
Hence dy/dx = dz/dx
We know that
x = cos2z
or, 2z = cos⁻¹x
or, 2 dz/dx = -1/√(1-x²)
Hence dy/dx = -1/ [2√(1-x²)]
The second equation is
\(y = 3tan^{-1}[x-\sqrt{1+x^{2}} ]\)
Let x = cotz
Hence we get
\(y = 3tan^{-1}[cotz-\sqrt{1+cot^{2}z} ]\)
\(y = 3tan^{-1}[cotz-\sqrt{cosec^{2}z} ]\)
or, y = 3tan⁻¹ [cotz - cosecz]
or, y = 3tan⁻¹ [cosz/sinx - 1/sinz]
or, y = 3tan⁻¹ [(cosz - 1)/sinz]
or, y = 3tan⁻¹ [-2sin²(z/2)/{2sin(z/2) cos(z/2)}]
or, y = 3tan⁻¹ [-sin(z/2)/cos(z/2)]
or, y = 3tan⁻¹ [-tan{z/2)]
or, y = 3tan⁻¹ [tan{-z/2)]
or, y = -3z/2
or, dy/dz = -3/2 dz/dx
We have
x = cotz
or, z = cot⁻¹z
or, dz/dx = -1/(1 + x²)
Hence we get
dy/dx = 3/[2(1 + x²)]
To learn more about differentiation visit
https://brainly.com/question/27986235
#SPJ4
7) What does a multiplier of \( 1.2 \) mean?
Answers
A multiplier of 1.2 means the value is multiplied or increased by a factor of 1.2.
A multiplier is a term used to represent a factor by which a value is multiplied or increased. It is a numeric value that indicates the extent of the increase or expansion of a given quantity. Multiplication by a multiplier results in scaling or changing the magnitude of the original value.
A multiplier of 1.2 indicates that a value will be increased by 20% or multiplied by a factor of 1.2. This means that when the multiplier is applied to the original value, the resulting value will be 1.2 times the original.
Read more about multipliers:
brainly.com/question/15883095
PLEASE HELP ME ASAP! THANK YOU
EXPLANATION = BRAINLIEST
The radius of a circle is 4 meters. What is the area of a sector bounded by a 135° arc?
Give the exact answer in simplest form.

Answers
Answer:
The area of the sector of the circle is approximately
Step-by-step explanation:
The given parameters of the circle having a shaded sector are;
The radius of the circle, r = 4 meters
The measure of the arc bounding the sector = 135°
The area of a sector of a circle, 'A', is given as follows;
\(A = \dfrac{\theta}{360 ^{\circ}} \times \pi \times r^2\)
Therefore, the area, 'A' of the given sector of the circle, is given as follows;
\(A = \dfrac{135 ^{\circ}}{360 ^{\circ}} \times \pi \times (4\ cm)^2 \approx 18.85 \ cm^2\)
The area of the sector of the circle, with radius 4 cm and bounded by an arc, A ≈ 18.82 cm².