Let f(x) 1 – x2 + 1 if x > Use sequential criterion to show lim f(x) doesn't exist. - 2 x +-2 (Hint: you don't need the graph of f(a) to answer this question).
Answers
To show that the limit of f(x) does not exist using the sequential criterion, we need to find two sequences (xn) and (yn) that converge to the same value c, but the corresponding sequences (f(xn)) and (f(yn)) do not converge to the same value.
Let's consider two sequences:
Sequence (xn): xn = 1/n
Sequence (yn): yn = -1/n
Both sequences (xn) and (yn) converge to 0 as n tends to infinity.
Now, let's evaluate the corresponding sequences (f(xn)) and (f(yn)):
Sequence (f(xn)): f(xn) = 1 - (1/n)^2 + 1 = 1 - 1/n^2 + 1 = 2 - 1/n^2
Sequence (f(yn)): f(yn) = -2 - (1/n)^2 + 1 = -2 - 1/n^2 + 1 = -1 - 1/n^2
As n tends to infinity, both sequences (f(xn)) and (f(yn)) approach 2. Therefore, both sequences converge to the same value.
However, the sequential criterion for the existence of a limit states that if a function has a limit as x approaches c, then the limit of the function must be the same for every sequence (xn) converging to c. In this case, since the sequences (f(xn)) and (f(yn)) do not converge to the same value (2 and -1, respectively), the limit of f(x) does not exist as x approaches 0.
Therefore, we have shown that the limit of f(x) does not exist using the sequential criterion.
To learn more about limit
https://brainly.com/question/29079489
#SPJ11
Related Questions
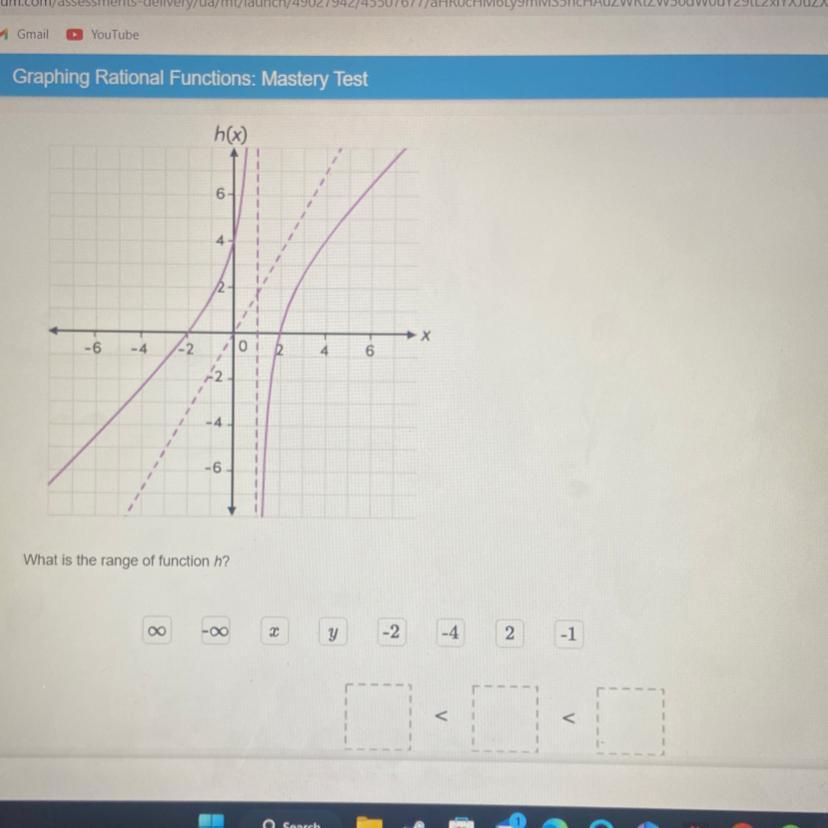
Drag the labels to the correct locations on the image. Not all lables will be used. Consider function h. What is the range of function h?
Answers
The range of the graphed function is expressed as: -∞ < y < ∞
How to find the range of the graph Function?Range corresponds to the values on the y-axis while the Domain corresponds to values on the x-axis.
From the graph of a function h(x), we want to find the range of the function in inequality notation.
The range is all possible y-values of the function. Thus, let's find all possible y-values from the graph.
If we look at the graph closely, we see that it has a vertical asymptote at x = 1 and a slant asymptote.
But it includes all y values from -infinity to infinity.
Thus, we can write range as -∞< y < ∞ because both sides of the function go and so on below the x-axis and go and so on above the x-axis.
The range is -∞< y < ∞ .
Read more about Range of Graph Function at: https://brainly.com/question/7954282
#SPJ1
Select all the terms which are equivalent to the slope in a proportional relationship.
Constant of proportionality
Origin
Inverse
Rise over run
The slope of a roof is called its pitch. The Parthenon, an ancient Greek temple, has a roof with a rise of 3.6 meters and a run of 12 meters. What is the pitch of the roof?
Answers
Answer:
Step-by-step explanation:
I would say: "Constant of proportionality" and "rise over run" would both descri=be slope. Certainly the latter one.
The pitch is rise/run (also called the slope in math) = 3.6 meters/12 meters = 0.3
There are 80 dogs and cats in the animal shelter. The ratio of dogs to cat 5/11 how many of animals are dogs
Answers
Answer:
Step-by-step explanation:
80/16x5=25
Find the value of the constant b that makes the following function continuous on (-[infinity]0,00). 3 f(x) = {3-5x+b ifz>3 3z 1
Answers
Therefore, the value of the constant b is 8.
To find the value of the constant b that makes the given function continuous on (-[infinity]0,00), we will use the limit property.
The limit property is an essential mathematical concept used to find the limit of a function. It's essentially a set of rules that govern how limits work and how we can manipulate them.
In our case, the function is:
f(x) = {3-5x+b if z > 3 ; 3z
if z ≤ 3
We need to find the value of the constant b that makes this function continuous on (-[infinity]0,00).
Let's start by finding the left-hand limit and right-hand limit of the function at z = 3.
Limit as z approaches 3 from the left:
f(3-) = lim f(z) as z → 3-Here z → 3- means z is approaching 3 from the left-hand side of 3.So when z < 3, the function is:f(z) = 3z
Now, let's find the limit of the function as z approaches 3 from the left:
f(3-) = lim f(z) as z → 3-
= lim 3z as z → 3-
= 3(3)
= 9
Limit as z approaches 3 from the right:
f(3+) = lim f(z) as z → 3+Here z → 3+ means z is approaching 3 from the right-hand side of 3.So when z > 3, the function is:f(z) = 3-5x+b
Now, let's find the limit of the function as z approaches 3 from the right:
f(3+) = lim f(z) as z → 3+
= lim (3-5x+b) as x → 3+
We don't know the value of b, so we can't find the limit yet.
However, we do know that the function is continuous at z = 3.
Therefore, the left-hand limit and right-hand limit must be equal:
f(3-) = f(3+)9
= 3-5(3)+b9
= -15 + b + 98
= b
Now we have found the value of the constant b that makes the function continuous on (-[infinity]0,00).
To know more about infinity visit:
https://brainly.com/question/22443880
#SPJ11
Algebra Challenge
1. Simplifying Expressions
Demam
The elementary school is building a new triangular playground that they want to
fence in. Given the three side lengths of 2x-1, 4x and 12x + 5 find the value of x
when the perimeter of the playground is 112 ft.
The situation can be represented by
nswer:
(2x-1)+4x+(12x+5)=114
Answers
Answer: Answer is 6.11
Step-by-step explanation:
Lets solve this equation (2x-1)+4x+(12x+5)=114
step 1: we first add x variables
ie. 2x + 4x + 12x = 18x
step 2: we add numbers
ie. -1 + 5 = 4
step 3: now we arrange LHS part
ie. 18x + 4 = 114
step 4: now move this 4 to right hand side and simplify them
ie. 18x = 114 - 4 = 110
step 5: now we divide 110 by 18 to get the value of x
ie. x = 110/18 = 6.11
Learn more about this question here: https://brainly.com/question/26174187?referrer=searchResults
Given the system x + 2z = -2
x + y + kz = 2
3x + ky - 2z = 2
(a) Give the augmented matrix for the system. (b) For which values of k (if any) does the system have a unique solution? (c) For which values of k (if any) does the system have a infinitely many solutions? (d) For which values of k (if any) does the system have a no solution?
Answers
b. The system has a unique solution when k is not equal to -2 or 10.
c. The system has infinitely many solutions when k = 10.
d. The system has no solution when k = -2.
The augmented system for the system is:
[1 0 2 -2]
[1 1 k 2]
[3 k -2 2]
The system to have a unique solution, the rank of the coefficient matrix must be equal to the rank of the augmented matrix.
Using row reduction to reduce the augmented matrix to echelon form, we get:
[1 0 2 -2]
[0 1 k+2 4]
[0 0 (k-10)/(k+2) 10]
So, the system has a unique solution when k is not equal to -2 or 10.
The system to have infinitely many solutions, the rank of the coefficient matrix must be less than the rank of the augmented matrix, and the last row of the echelon form of the augmented matrix must be all zeros.
This occurs when:
(k-10)/(k+2) = 0
which happens when k = 10.
So, the system has infinitely many solutions when k = 10.
The system to have no solution, the last row of the echelon form of the augmented matrix must have a non-zero constant on the right-hand side.
This occurs when:
(k-10)/(k+2) ≠ 0
True for all values of k except k = -2. So, the system has no solution when k = -2.
For similar questions on system
https://brainly.com/question/25976025
#SPJ11
(a) The augmented matrix for the system is: [1 0 2 | -2] [1 1 k | 2] [3 k -2 | 2] (b) The system has a unique solution when the determinant of the coefficient matrix is nonzero.
In this case, the determinant is 2k + 3. Therefore, the system has a unique solution for any value of k except k = -3/2. (c) The system has infinitely many solutions when the determinant of the coefficient matrix is zero, and the system is consistent (i.e., the right-hand side of each equation is consistent with the others).
In this case, when k = -3/2, the determinant becomes zero, and the system has infinitely many solutions.
(d) The system has no solution when the determinant of the coefficient matrix is zero, and the system is inconsistent (i.e., the right-hand side of at least one equation is inconsistent with the others). In this case, there are no specific values of k that make the system inconsistent.
To determine the unique solution, infinitely many solutions, or no solution for the system, we analyze the determinant of the coefficient matrix. If the determinant is nonzero, there is a unique solution. If the determinant is zero and the system is consistent, there are infinitely many solutions. If the determinant is zero and the system is inconsistent, there is no solution.
To learn more about augmented matrix click here
brainly.com/question/30403694
#SPJ11
Hi guys i need help with this problem y=mx+b
Answers
x = how far along
m = Slope or Gradient (how steep the line is)
b = value of y when x=0
How do you find "m" and "b"?
b is easy: just see where the line crosses the Y axis.
m (the Slope) needs some calculation:
m = Change in Y/change in X
BRAINLIEST
a. 45
b. 34
c. 29
d. 56

Answers
Find x to the nearest degree
Answer:a. 45
A triangle has a side that is 5 inches long that is adjacent to an angle of 61. In addition, the side oppositethe 61 angle is 4,8 inches long. There are two triangles with these measurements. For each one,determine the other two angles of the triangle and the length of the third side..acute:(a) The triangle in which the angle opposite the 5-inch side-The angle between the two given sides measuresnearest tenth of a degree.)The third angle measuresThe remaining side is approximatelyan inch.)(b) The triangle in which the angle opposite the 5-inch side is obtuse:The angle between the two given sides measuresnearest tenth of andegree.)WThe third angle measuresThe remaining side is approximatelyan inch.)degrees. (Round to thedegrees. (Round to the nearest tenth of a degree.)Ainches long. (Round to the nearest tenth ofdegrees. (Round to thedegrees. (Round to the nearest tenth of a degree.)inches long. (Round to the nearest tenth of an inch
Answers
The two remaining angles are 58°, and the length of the third side of the triangle is 6.5 inch.
In order to determine the other two angles of each triangle as well as the length of the third side, we need to use the Cosine Rule. According to the Cosine Rule, for any triangle with sides of length a, b, and c, and angles of A, B, and C, the following equation holds:
\(c^2 = a^2 + b^2 - 2ab cos(C)\)
For the first triangle, we are given that the side of length 5 is adjacent to an angle of 61°. Therefore, a = 5, C = 61°. Using the information provided, we can also determine that b = 4.8. Substituting these values into the Cosine Rule equation, we get:
\(c^2 = (5)^2 + (4.8)^2 - 2(5)(4.8) cos(61°)\)
We can solve this equation to get c = 6.5. Therefore, the length of the third side in the first triangle is 6.5. Additionally, we can use the Triangle Angle Sum theorem to determine the other two angles. According to this theorem, the sum of the three angles of a triangle is 180°. Therefore, for the first triangle, the two remaining angles are 180 - 61 - (180 - 61) = 58°.
For the second triangle, we use the same process, but with the given side lengths reversed. That is, we set a = 4.8, b = 5, and C = 61°. Again, substituting these values into the Cosine Rule equation, we get:
\(c^2 = (4.8)^2 + (5)^2 - 2(4.8)(5) cos(61°)\)
We can solve this equation to get c = 6.5. Therefore, the length of the third side in the second triangle is also 6.5. We can use the Triangle Angle Sum theorem again to determine the other two angles. Again, for the second triangle, the two remaining angles are 180 - 61 - (180 - 61) = 58°.
In conclusion, for each triangle, the two remaining angles are 58°, and the length of the third side is 6.5 inch.
Learn more about cosine rule: https://brainly.com/question/21568111
#SPJ11
Prove that if f is differentiable at a, then |f| is also differentiable at a, provided that f(a)≠0
Answers
If a function f is differentiable at a point a and f(a) is not equal to zero, then the absolute value function |f| is also differentiable at that point.
The proof involves considering two cases based on the sign of f(a) and showing that the limit of the difference quotient exists for |f| at point a in both cases. However, it is important to note that |f| is not differentiable at the point where f(a) equals zero.
To prove that if f is differentiable at a, then |f| is also differentiable at a, provided that f(a) ≠ 0, we need to show that the limit of the difference quotient exists for |f| at point a.
Let's consider the function g(x) = |x|. The absolute value function is defined as follows:
g(x) = {
x if x ≥ 0,
-x if x < 0.
Since f(a) ≠ 0, we can conclude that f(a) is either positive or negative. Let's consider two cases:
Case 1: f(a) > 0
In this case, we have g(f(a)) = f(a). Since f is differentiable at a, the limit of the difference quotient exists for f at point a:
lim (x→a) [(f(x) - f(a)) / (x - a)] = f'(a).
Taking the absolute value of both sides, we have:
lim (x→a) |(f(x) - f(a)) / (x - a)| = |f'(a)|.
Since |g(f(x)) - g(f(a))| / |x - a| = |(f(x) - f(a)) / (x - a)| for f(a) > 0, the limit on the left-hand side is equal to the limit on the right-hand side, which means |f| is differentiable at a when f(a) > 0.
Case 2: f(a) < 0
In this case, we have g(f(a)) = -f(a). Similarly, we can use the same reasoning as in Case 1 and conclude that |f| is differentiable at a when f(a) < 0.
Since we have covered both cases, we can conclude that if f is differentiable at a and f(a) ≠ 0, then |f| is also differentiable at a.
Note: It's worth mentioning that at the point where f(a) = 0, |f| is not differentiable. The proof above is valid when f(a) ≠ 0.
To know more about differentiable refer to-
https://brainly.com/question/13958985
#SPJ11
The ratio of a to b is constant, and
a = 9 when b = 6. What is the value of
b when a = 2?
Answers
Answer:
Step-by-step explanation:
a : b
9 : 6
2 : x
Cross multiply
6*2 = 9x
12 = 9x
12/9 = x
4/3 = x
Cinema a sells a 12-pack of movie passes for $66 Cinema be so there's a 5-pack of movie passes for $28 what is the cost per movie pass for each Cinema which offers cheaper per MoviePass how much do you say for MoviePass if you choose the cheaper offer
Answers
Let a pack of movie pass by Cinema A be represented with a,
and a pack of movie pass by Cinema B be represented with b.
So,
\(\begin{gathered} 12a=66 \\ \text{Divide both sides by 12, we get} \\ a=\frac{66}{12}=\text{ 5.5 = \$5.50} \end{gathered}\)\(\begin{gathered} 5b\text{ =28} \\ \text{Divide both sides by 5, we get} \\ b=\frac{28}{5}=5.6=\text{ \$5.60} \end{gathered}\)Hence, the cost per pack of movie pass by Cinema A is $5.50, while the cost per pack of movie pass by Cinema B is $5.60.
Cinema A offer per pack of movie pass is cheaper compare to Cinema B price.
So, 5.60 - 5.50 = 0.10
You save $0.10 per movie pass if you choose the cheaper offer ( Cinema A offer)
Simplify the Radical Expression
3V2 - V8 +4V12+53

Answers
The density of water is 1000 kilograms per cubic meter, and the density of ice is about 916 kilograms per cubic meter. If 575 kilograms of water and 275 kilograms of ice is combined in a container, about how much volume would the mixture take up?
A)5.0 m^3
B)2.3 m^3
C)0.9 m^3
D)0.4 m^3
Answers
Answer:
Step-by-step explanation:
Its c
the vertices of triangle wxy are located at w(-14,20). x(10,4) and y (-2,-4). what is the approximate length of the midsegment parallel to xy?
Answers
The approximate length of the midsegment parallel to xy is 6.63
The midsegment of a triangle is a line segment that connects the midpoints of two sides of the triangle and has the same length as each of the two sides.
To find the midpoint of a line segment, we average the x-coordinates and the y-coordinates of its endpoints.
Since the question stated that the midsegment is parallel to xy, we need to find midpoint of xw and yw.
First, let's find the midpoint of side xw:
Midpoint of xw : ((-14+10)/2, (20+4)/2) = (-2, 12)
Midpoint of yw : ((-14-2)/2, (20-4)/2) = (-8, 8 )
The length of a line segment between two points (x1, y1) and (x2, y2) in a two-dimensional coordinate system can be calculated using the distance formula:
d = √((x2 - x1)^2 + (y2 - y1)^2)
Length line of midpoint xw and midpoint yw :
√((-2-(-8))^2 + (12-(8))^2) = √(6^2 + 4^2) = √(36 + 8) = √44
So, the length of the midsegment is parallel to XY, which is approximately equal to √44 = 6.63
Learn more about midsegment of triangle here
https://brainly.com/question/21103382
#SPJ4
Question 4 Multiple Choice Worth 5 points)
Simplify by dividing
(-5/8) divided by (-3/4)
A. 20/24
B. -20/24
C. -15/32
D. 15/32
Answers
Answer:
0.0520833333 is the "techical answer" but the real answer is B
Step-by-step explanation:
if you do the math -5 x 4 / 8 x -3 = -20/24
Hope this helps :)
The table shows the price of applause in the local market what is the cost of 12 pounds of apples

Answers
Answer:
18
Step-by-step explanation:
if 4 = 6
multiply them both by 3
and you get 12 = 18
2a−1/2
please help me :(
Answers
Answer:
this is unsolvable i think
Step-by-step explanation:
lex is planning to surround his pool abcd with a single line of tiles. how many units of tile will he need to surround his pool? round your answer to the nearest hundredth. a coordinate plane with quadrilateral abcd at a 0 comma 4, b 3 comma 5, c 5 comma negative 1, and d 2 comma negative 2. angles a and c are right angles, the length of segment ab is 3 and 16 hundredths units, and the length of diagonal bd is 7 and 7 hundredths units.
Answers
Lex will need approximately 18.96 units of tile to surround his pool. The perimeter of the quadrilateral is the sum of these lengths.
To find the number of units of tile Lex will need to surround his pool, we can calculate the perimeter of the quadrilateral ABCD.
Given the coordinates of the vertices on the coordinate plane, we can calculate the lengths of the sides:
AB = \(\sqrt((3-0)^2 + (5-4)^2) = \sqrt(9+1) = \sqrt(10)\) = 3.16 units (rounded to the nearest hundredth)
BC = \(\sqrt((5-3)^2 + (-1-5)^2) = \sqrt(4+36) = \sqrt(40)\) = 6.32 units (rounded to the nearest hundredth)
CD = \(\sqrt((2-5)^2 + (-2+1)^2) = \sqrt(9+1) = \sqrt(10)\) = 3.16 units (rounded to the nearest hundredth)
DA = \(\sqrt((2-0)^2 + (-2-4)^2) = \sqrt(4+36) = \sqrt(40)\) = 6.32 units (rounded to the nearest hundredth)
The perimeter of the quadrilateral is the sum of these lengths:
Perimeter = AB + BC + CD + DA = 3.16 + 6.32 + 3.16 + 6.32 = 18.96 units (rounded to the nearest hundredth)
Therefore, Lex will need approximately 18.96 units of tile to surround his pool.
To know more about perimeter visit:
https://brainly.com/question/30252651
#SPJ11
Lex will need approximately 20.46 units of tile to surround his pool. To find the number of units of tile needed to surround the pool, we need to calculate the perimeter of the pool.
Given the coordinates of the four vertices of the pool:
A(0, 4)
B(3, 5)
C(5, -1)
D(2, -2)
We can find the length of segment AB using the distance formula:
\(AB = \sqrt{(3-0)^2 + (5-4)^2} = \sqrt{9 + 1} = \sqrt{10} = 3.16\)units (rounded to the nearest hundredth).
The length of diagonal BD can also be found using the distance formula:
\(BD = \sqrt{(2-3)^2 + (-2-5)^2} = \sqrt{1 + 49} = \sqrt{50} = 7.07\) units (rounded to the nearest hundredth).
Since angles A and C are right angles, we know that the opposite sides AB and CD are parallel. Similarly, the opposite sides AD and BC are parallel.
The perimeter of the pool is the sum of the lengths of all four sides:
Perimeter = AB + BC + CD + AD
= 3.16 + BD + 3.16 + BD
= 6.32 + 7.07 + 7.07
= 20.46 units (rounded to the nearest hundredth).
Therefore, Lex will need approximately 20.46 units of tile to surround his pool.
Learn more about distance formula from the given link:
https://brainly.com/question/32846365
#SPJ11
Store A sells 2 packages of straberries for $4.98.
Store B sells 5 packages of strawberries for $11.25.
Which store sells them at a cheaper price per package? How much cheaper is it?
Answers
Answer:
31
Step-by-step explanation:
Answer:
Store B and Its $1.20 cheaper if you buys five packs of strawberries from store B
Two friends, Bart and Claudia, purchased concessions at a basketball game.
Bart purchased 2 drinks and 2 candy bars for a total of $5.00.
Claudia purchased 1 drink and 4 candy bars for a total of $4.75.
Which statement is true?
Drinks cost $1.75 each, and candy bars cost $0.75 each.
Drinks cost 1 point 7 5 dollars each, and candy bars cost 0 point 7 5 dollars each.
Drinks cost $0.75 each, and candy bars cost $1.75 each.
Drinks cost 0 point 7 5 dollars each, and candy bars cost 1 point 7 5 dollars each.
Drinks cost $1.25 each, and candy bars cost $1.25 each.
Drinks cost 1 point 2 5 dollars each, and candy bars cost 1 point 2 5 dollars each.
Drinks cost $1.00 each, and candy bars cost $0.75 each.
Answers
The Drink cost $1.75 each, and candy bars cost $0.75 each.
let
The price of a drink = x
The price of a candy bar = y
Bart total purchase
2x + 2y = 5Claudia total purchase
x + 4y = 4.75The cost of each can be calculated by combining the equations. Therefore,
2x + 2y = 5
x + 4y = 4.75
x = 4.75 - 4y
2(4.75 - 4y) + 2y = 5
9.5 - 8y + 2y = 5
9.5 - 6y = 5
-6y = -4.5
y = -4.5/-6
y = 0.75
2(0.75) + 2x = 5
1.5 + 2x = 5
2x = 5 - 1.5
2x = 3.5
x = 3.5/2
x = 1.75
Cost of a drink = $1.75
Cost of a candy bars = $0.75
Get more information here: https://brainly.com/question/12471733?referrer=searchRes
Thriteen Is at least the difference of a number V and 1
Answers
Answer:
14
Step-by-step explanation:
peter is now 12 years old and john is 3 years old . in how many years will peter be twice as old as john
Answers
Step-by-step explanation:
Peter = 12 years
John = 3 years
peter twice John = ( 12×3)
Peter will be 36 years.
The circumference of a circular field is 166.42 yards what is the diameter of the field
Answers
The circumference of the circle field is given, to find the diameter the formula must be applied where the diameter of the circle is found by dividing the circumference with 3.14, the result is approximately 52.97
The diameter of the circle is the longest ray that is twice of radius. The circumference of the circle must be divided with the \(\pi\) value to find the diameter of the circle. As it is known that the circumference of the circle is 2 times the value of \(\pi\)and radius and the diameter is two time the radius hence the formula of finding the diameter when the circumference is given will be: d = C/\(\pi\)
Here d stands for diameter, C stands for circumference
The value of \(\pi\) is 3.14
Where C= 2\(\pi\)r
and d= 2r
so the formula of diameter is
d= C/\(\pi\)
d= 166.42/3.14
d= 52.97313
that can be approximately taken as 52.97
So when the circumference of the circular filed is 166.42 then the diameter of the field is 52.97. The diameter can also be said as the half of the radius and the relation between the circumference and the ratio between the value of pi and diameter.
To know more about calculating diameter when the circumference is given follow the link below:
https://brainly.com/question/32048386
#SPJ4
Which fraction is equivalent to 5/20
Answers
Answer:
1/4
Step-by-step explanation:
You can simplify 5/20 by dividing the numerator and denominator by 5 and getting 1/4
Step-by-step explanation:
The answer is going to be 1/4
A model rocket is launched from a raised platfo. Its height in feet is given by H=−16t 2
+96t+288(t= seconds after launch ) After how many seconds will the rocket hit the ground? Round to 1 decimal place. 2.0 seconds 8.2 seconds 3.0 seconds 2.2 seconds
Answers
To find the time it takes for the rocket to hit the ground, we need to determine when the height (H) becomes zero. We can set the equation -16t^2 + 96t + 288 = 0 and solve for t.
Using the quadratic formula, which states that for an equation of the form ax^2 + bx + c = 0, the solutions are given by:
x = (-b ± √(b^2 - 4ac)) / (2a)
In this case, we have a = -16, b = 96, and c = 288. Plugging these values into the quadratic formula, we get:
t = (-96 ± √(96^2 - 4(-16)(288))) / (2(-16))
Simplifying further:
t = (-96 ± √(9216 + 18432)) / (-32)
t = (-96 ± √(27648)) / (-32)
t = (-96 ± 166.272) / (-32)
Using the positive square root:
t = (-96 + 166.272) / (-32)
t = 70.272 / (-32)
t ≈ -2.2 seconds
The negative value of t does not make sense in this context since time cannot be negative. Therefore, we discard the negative solution.
Hence, the rocket will hit the ground after approximately 2.2 seconds.
Learn more about quadratic formula here:
brainly.com/question/22364785
#SPJ11
What is the value of x in the equation, 0.25x + 7 = 4(x – 2)
Answers
Answer:
4
Step-by-step explanation:
0.25x + 7 = 4(x-2)
0.25x + 7 = 4x - 8
0.25x - 4x = -7 - 8
-3.75x = -15
3.75x = 15
x = 4
The functions f(x) and g(x) are shown on the graph.
fx) = x²
What is g(x)?
10-
у
g(x)
f(x)
5
(1,4)
+
10
-5
5
-5
-10
O A. g(x) = 4x²
B. g(x) = (3x)2
O C. g(x) = (x+4)2
D. g(x) = (x - 4)2

Answers
Answer:
A
Step-by-step explanation:
it goes through the vertex so that means it is not moved so that rules out C and d
seeing the y value for 1 is 4 that means that it has to be A
Answer:
A
Step-by-step explanation:
by using the eqn to find for a straight line
slope = ∆y/∆x
(1,4) and (0,0) since both points are in the line
slope = 4
then,
y-y'=slope(x-x')
y-4=4(x-1)
y-4=4x-4
y=4x-4+4
y=4x
but the graph is parabolic thus
y=4x^2
this is how I did it I have no idea to do anything else so hope it works
Let be the linear transformation which reflects all vectors in through the xy plane. Find a matrix for and then obtain its eigenvalues and eigen…
Let be the linear transformation which reflects all vectors in through the xy plane. Find a matrix for and then obtain its eigenvalues and eigenvectors.
Answers
any nonzero vector in R^3 can be an eigenvector of T with eigenvalue λ = -1. For example, the vector (1, 0, 0) is an eigenvector of T with eigenvalue λ = -1, since T sends it to its negative (-1, 0, 0). Similarly, (0, 1, 0) and (0, 0, 1) are also eigenvectors of T with eigenvalue λ = -1.
To find the matrix for the linear transformation T that reflects all vectors in R^3 through the xy plane, we first need to determine how T affects the standard basis vectors.
T sends the vector (1, 0, 0) to (-1, 0, 0), since reflecting across the xy-plane negates the z-coordinate. Similarly, T sends (0, 1, 0) to (0, -1, 0), and (0, 0, 1) to (0, 0, -1). Therefore, the matrix for T with respect to the standard basis is:
[T] = [ -1 0 0 ]
[ 0 -1 0 ]
[ 0 0 -1 ]
To find the eigenvalues and eigenvectors of T, we can solve the characteristic equation:
det([T] - λ[I]) = 0
where I is the 3x3 identity matrix. Substituting the matrix for T and expanding the determinant, we get:
det([T] - λ[I]) = det([ -1-λ 0 0 ])
det([ 0 -1-λ 0 ])
det([ 0 0 -1-λ ])
= (-1-λ)(-1-λ)(-1-λ)
= -(λ+1)^3
Therefore, the only eigenvalue of T is λ = -1, and we need to find its eigenvectors. To do this, we need to solve the system of equations:
([T] - (-1)[I])v = 0
Substituting the matrix for T and the eigenvalue λ = -1, we get:
[ 0 0 0 ][x] [0]
[ 0 0 0 ][y] = [0]
[ 0 0 0 ][z] [0]
This system of equations has a rank of 0, which means that there are infinitely many solutions.
To learn more about vector visit:
brainly.com/question/24256726
#SPJ11
Please help‼️ domain and range‼️

Answers
The domain and the range of the function are (-∝, ∝) and (0, ∝), respectively
Calculating the domain and range of the graph?From the question, we have the following parameters that can be used in our computation:
The graph
The above graph is an exponential function
The rule of an function is that
The domain is the set of all real values
In this case, the domain is (-∝, ∝)
For the range, we have
Range = (0, ∝)
Read more about domain and range at
brainly.com/question/27910766
#SPJ1