Let f(x)= (x+3)^2/x^2-9. Find a) lim x→-3 f(x), b) lim x→0 f(x), and c) lim x→3 f(x).
Answers
a) lim x→-3 f(x) = 0
b) lim x→0 f(x) = -1
c) lim x→3 f(x) = DNE
To find the limits of the function f(x) = (x + 3)² / (x² - 9) as x approaches certain values, we evaluate the function using the following steps:
a) lim x→-3 f(x):
Substitute -3 into the function:
lim x→-3 f(x) = lim x→-3 [(x + 3)² / (x² - 9)].
Since the denominator (x² - 9) becomes zero at x = -3, we have an indeterminate form.
To evaluate this limit, we can simplify the function:
lim x→-3 f(x) = lim x→-3 [(x + 3)² / (x - 3)(x + 3)].
Cancel out the common factors:
lim x→-3 f(x) = lim x→-3 (x + 3) / (x - 3).
Now we can directly substitute x = -3:
lim x→-3 f(x) = (-3 + 3) / (-3 - 3) = 0 / (-6) = 0.
b) lim x→0 f(x):
Substitute 0 into the function:
lim x→0 f(x) = lim x→0 [(x + 3)² / (x² - 9)].
Again, the denominator (x² - 9) becomes zero at x = -3, so we have an indeterminate form.
Simplify the function:
lim x→0 f(x) = lim x→0 [(x + 3)² / (x - 3)(x + 3)].
Cancel out the common factors:
lim x→0 f(x) = lim x→0 (x + 3) / (x - 3).
Now we can directly substitute x = 0:
lim x→0 f(x) = (0 + 3) / (0 - 3) = 3 / (-3) = -1.
c) lim x→3 f(x):
Substitute 3 into the function:
lim x→3 f(x) = lim x→3 [(x + 3)² / (x² - 9)].
Since the denominator (x²- 9) becomes zero at x = 3, we have an indeterminate form.
Simplify the function:
lim x→3 f(x) = lim x→3 [(x + 3)² / (x - 3)(x + 3)].
Cancel out the common factors:
lim x→3 f(x) = lim x→3 (x + 3) / (x - 3).
Now we can directly substitute x = 3:
lim x→3 f(x) = (3 + 3) / (3 - 3) = 6 / 0 = undefined (or DNE).
To know more about functions, visit:
https://brainly.com/question/30956864
#SPJ11
Related Questions
Can I get some help plz

Answers
Answer:
3rd choice
Step-by-step explanation:
3. Callum rolled a single six sided die 12 times and it landed on a six, three of the times. The probability that it will land on a six on the 13th roll is?
Answers
Answer:
1/6
Step-by-step explanation:
Each roll is independent. So the probability of rolling a six is 1/6, regardless of the previous rolls.
What
is the difference between Variance and Standard Deviation?
Give
examples of how they are applied.
Answers
Variance and standard deviation are both measures of the dispersion or spread of a dataset, but they differ in terms of the unit of measurement.
Variance is the average of the squared differences between each data point and the mean of the dataset. It measures how far each data point is from the mean, squared, and then averages these squared differences. Variance is expressed in squared units, making it difficult to interpret in the original unit of measurement. For example, if we are measuring the heights of individuals in centimeters, the variance would be expressed in square centimeters.
Standard deviation, on the other hand, is the square root of the variance. It is a more commonly used measure because it is expressed in the same unit as the original data. Standard deviation represents the average distance of each data point from the mean. It provides a more intuitive understanding of the spread of the dataset. For example, if the standard deviation of a dataset of heights is 5 cm, it means that most heights in the dataset are within 5 cm of the mean height.
To illustrate the application of these measures, consider a dataset of test scores for two students: Student A and Student B.
If Student A has test scores of 80, 85, 90, and 95, and Student B has test scores of 70, 80, 90, and 100, we can calculate the variance and standard deviation for each student's scores.
The variance for Student A's scores might be 62.5, and the standard deviation would be approximately 7.91. For Student B, the variance might be 125 and the standard deviation would be approximately 11.18.
These measures help us understand how much the scores deviate from the mean, and how spread out the scores are within each dataset.
Learn more about standard deviation here:-
https://brainly.com/question/23986929
#SPJ11
jim is six feet tall, and his shadow is $16$ feet long. the flagpole he is standing next to casts a shadow that is $72$ feet long. how tall is the flagpole, in feet?
Answers
The height of the flagpole is 27 feet.
Given,
If two triangles are similar, sides of these triangles will be proportional.
Height of the flagpole = h feet
Shadow castes by the flagpole = 72 feet
Height of the person = 6 feet
Shadow casted by the person = 16 feet
By using the property of similar triangles,
Hence, h/6 = 72/16
h = (6×72)/ 16
h = 27 feet
Therefore, The height of the flagpole is 27 feet.
Learn more about Triangles at:
https://brainly.com/question/2773823
#SPJ1
Suppose n∈N and z∈C with ∣z∣=1 and z 2n =/=−1. Prove that z^n/1+z 2n ∈R.
Answers
(1 + z^(2n))* is equal to (1 - z^(2n)) or its square. Hence, z^n/(1 + z^(2n)) can be converted to a real number, Therefore, z^n/(1 + z^(2n)) is a real number.
Given that n ∈ N and z ∈ C with |z| = 1 and z^(2n) ≠ -1, we need to prove that z^n/(1 + z^(2n)) ∈ R.
Let's take the conjugate of the denominator 1 + z^(2n). We know that for any complex number a + bi, its conjugate is given by a - bi.
Now, the conjugate of 1 + z^(2n) is 1 - z^(2n), and this is true for all values of z as z has magnitude 1.
Thus, (1 + z^(2n)) + (1 - z^(2n)) = 2 is real.
Also, z^n is a complex number as z is a complex number. Let's write z^n as cos(nx) + isin(nx), where x is some real number.
Now, z^n/(1 + z^(2n)) = (cos(nx) + isin(nx))/2, hence it is a complex number.
Dividing by a real number will convert the result into a real number. We can obtain a real number by taking the conjugate of the denominator (1 + z^(2n)) and multiplying the numerator and the denominator with it, because (1 + z^(2n))(1 - z^(2n)) = 1 - z^(4n). Let's call this C.
Let's take the conjugate of C, which is C* = (1 + z^(2n))* (1 - z^(2n))* = (1 - z^(2n))(1 - z^(2n)*).
Now, z^(2n) + z^(2n)* = 2cos(2nx), which is a real number.
So, C* = (1 - z^(2n))(1 - z^(2n)* ) = (1 - z^(2n))(1 - z^(2n)) = (1 - z^(2n))^2 is a non-negative real number, as the square of a real number is non-negative.
Thus, (1 + z^(2n))* is equal to (1 - z^(2n)) or its square. Hence, z^n/(1 + z^(2n)) can be converted to a real number.
Therefore, z^n/(1 + z^(2n)) is a real number.
Learn more about real number.
https://brainly.com/question/17019115
#SPJ11
Scale Factor: 1/2; Center: point N

Answers
The new coordinates of points M and O is determined as;
M = (0.5, - 1)
O = (2.5, -2).
What is the new coordinate of points of M and O?The new coordinate of points M and O after applying the scale factor is calculated as follows;
The given scale factor = 1/2
The current coordinates of point M and O is;
M = (1, - 2)
O = (5, - 4)
A scale factor can be used to either enlarge a figure or decrease a figure.
When the scale factor is less than 1, it means the new figure will be smaller than the original figure.
However, if the scale factor is greater than 1, the new figure will be greater than the original figure.
The new coordinates of points M and O is determined as follows;
M = (1 x 1/2, -2 x 1/2) = (0.5, - 1)
O = (5 x 1/2, -4 x 1/2) = (2.5, -2)
Learn more about scale factor here: https://brainly.com/question/2826496
#SPJ1
How do you calculate obtuse value?.
Answers
Calculating the obtuse angle or value of a triangle.
Finding obtuse angle value:
steps:
1) Square the length of both sides of the triangle that intersect to create the obtuse angle, and add the squares together.
For example, if the lengths of the sides measure 4 and 2, then squaring them would result in 16 and 4. Adding the squares together results in 20.
2) Square the length of the side opposite the obtuse angle. For the example, if the length is 5, then squaring it results in 25.
3) Subtract the combined squares of the adjacent sides by the square of the side opposite the obtuse angle. For the example, 25 subtracted from 20 equals -5.
4) Multiply the lengths of the adjacent sides together, and then multiply that product by 2. For the example, 4 multiplied by 2 equals 8, and 8 multiplied by 2 equals 16.
5) Divide the difference of the sides squared by the product of the adjacent sides multiplied together then doubled. For the example, divide -5 by 16, which results in -0.3125.
The obtuse angle value is obtained by inverse of cos:
cos^-1(-0.3125)
= 108.209 degrees.
Learn more about the obtuse here:
https://brainly.com/question/1581660
#SPJ4
What is the sum of the first 12 terms in the series shown below?
1.5 - 4.5 + 13.5 - 10.5 +
Answers
How do you find the area of a circle with a rectangle?
Answers
the area of a circle with a rectangle will be [π w²2]/4.
What is the area of a circle?
The measurement of the circle's boundaries is called as the circumference or perimeter of the circle. whereas the circumference of a circle determines the space it occupies. The circumference of a circle is its length when it is opened up and drawn as a straight line. Units like cm or unit m are typically used to measure it. The circle's radius is considered while calculating the circumference of the circle using the formula. As a result, in order to calculate the circle's perimeter, we must know the radius or diameter value.
area of the circle will be πr².
The area of a circle inscribed in a rectangle if the length of the rectangle is l and the width is w
= [π w²2]/4.
Hence the area of a circle with a rectangle will be [π w²2]/4.
Learn more about area of a circle, by the following link.
https://brainly.com/question/17380589
#SPJ4
Selena has a piece of ribbon that is 130 inches long. If she wants to make bracelets that are 9 inches long, how many inches of ribbon will be left over?
Answers
Answer:
Yes dentro as options out not is me viking one produtions
\(14 \frac{4}{9}\) inches of ribbon will be left over.
What is division?Creating equal groupings or determining how many people go into each group after a fair distribution is the basic objective of division. Multiply the first percentage by the equivalent of the other to equal the quadratic formula. They factor everything and search for common traits after rewriting the partition as multiple of the first statement by the opposite of the latter.
Selena has a 130-inch-long ribbon in her possession.
If she strives to make 9-inch bracelets,
ribbon will be left over = 130/9
= \(14 \frac{4}{9}\)
In the end, Selena will have \(14 \frac{4}{9}\) a ribbon left with her.
Learn more about division, Here:
https://brainly.com/question/21416852
#SPJ2
The remains of an ancient ball court include a rectangular playing alley with a perimeter of about 24m. The length of the alley is three times the width. Find the length and the width of the playing alley.The width is ? m and the length is ? m
Answers
ANSWER
Length of the playing alley = 9m
Width of the playing alley = 3m
STEP-BY-STEP EXPLANATION:
Given information
The perimeter of a rectangular playing alley = 24 m
The length of the alley is three times the width
Let l represents the length of the alley
Let w represents the width of the alley
Step 1: Write the formula for calculating the perimeter of a rectangle
\(\text{Perimeter of a rectangle = 2(l + w)}\)Where l is the length and w is the width of the rectangle
Recall, length = 3 times the width of the alley
Mathematically,
\(\begin{gathered} l\text{ = 3 }\times\text{ w} \\ l\text{ = 3w} \end{gathered}\)Step 2: Substitute the value of l = 3w into the above formula
\(\begin{gathered} P\text{ = 2(l + w)} \\ p\text{ = 24m} \\ l\text{ = 3w} \\ 24\text{ = 2(3w + w)} \end{gathered}\)Step 3: Solve for w
\(\begin{gathered} 24\text{ = 2(4w)} \\ 24\text{ = 8w} \\ \text{Divide both sides by 8} \\ \frac{24}{8}\text{ = }\frac{8w}{8} \\ w\text{ = 3 m} \end{gathered}\)From the calculations above, you will see that the width of the playing alley is 3m
Step 4: Solve for l
\(\begin{gathered} \text{Recall, l = 3w} \\ w\text{ = 3} \\ l\text{ = 3 }\times3 \\ l\text{ = 9m} \end{gathered}\)Hence, the length of the playing alley is 9m
Which expression is equivalent to (4.3x + 4)(−1.8x)?
Answers
The expression which is equivalent to the given expression is -7.74x² - 7.2x.
The given expression is (4.3x + 4)(−1.8x).
What is an equivalent expression?Equivalent expressions are expressions that work the same even though they look different. If two algebraic expressions are equivalent, then the two expressions have the same value when we plug in the same value for the variable.
Now, the given expression can be solved as follows:
(4.3x + 4)(−1.8x)
Using distributive property
4.3x × (−1.8x) + 4 × (−1.8x)
= -7.74x² - 7.2x
Therefore, the expression which is equivalent to the given expression is -7.74x² - 7.2x.
To learn more about the equivalent expression visit:
https://brainly.com/question/28170201.
#SPJ1
24 pennies to 60 pennies
Answers
Answer:
24 x 2.5 = 60...
Step-by-step explanation:
sorry if this is wrong...
have a good day
Pls help with this answer

Answers
When b is 3, the value of the expression \(2b^3 + 5\) is 59.
To evaluate the expression\(2b^3 + 5\) when b is 3, we substitute the value of b into the expression and perform the necessary calculations.
Given that b = 3, we substitute this value into the expression:
\(2(3)^3 + 5\)
First, we evaluate the exponent, which is 3 raised to the power of 3:
2(27) + 5
Next, we perform the multiplication:
54 + 5
Finally, we add the two terms:
59
Therefore, when b is 3, the value of the expression \(2b^3 + 5\) is 59.
In summary, by substituting b = 3 into the expression \(2b^3 + 5\), we find that the value of the expression is 59.
It's important to note that the provided equation has multiple possible solutions for x, but when b is specifically given as 3, the value of x is approximately 3.78.
It's important to note that in this equation, we substituted the value of b and solved for x, resulting in a specific value for x. However, if we wanted to solve for b given a specific value of x, we would follow the same steps but rearrange the equation accordingly.
For more such question on expression visit:
https://brainly.com/question/1859113
#SPJ8
Compute the tolerance interval for capturing at least 90% of the values in a normal distribution with the confidence level of 95%. Round your answers to two decimal places (e.g. 98.76).
Answers
Thus, with 95% confidence that at least 90% of the values in a normal distribution fall within the tolerance interval of mean +/- 0.10.
We can use a standard normal distribution table to find the critical values, which is the z-score that corresponds to the given confidence level. For a 95% confidence level, the critical value is 1.96.
Next, we need to find the standard deviation of the normal distribution. We can use the formula:
tolerance interval = mean +/- z * (standard deviation / sqrt(n))
where mean is the mean of the distribution, z is the critical value, standard deviation is the standard deviation of the distribution, and n is the sample size. Since we don't have a sample size, we can assume a large sample size and use the population standard deviation instead.
Assuming a population standard deviation of 1, the tolerance interval is:
tolerance interval = mean +/- 1.96 * (1 / √(n))
To capture at least 90% of the values, we need to set the tolerance interval to be equal to 90%.
0.90 = 1.96 * (1 / √(n))
Solving for n, we get:
n = (1.96 / 0.10)^2
n = 384.16
Since we assumed a large sample size, we can round up to the nearest integer, which gives us a sample size of 385.
The tolerance interval for capturing at least 90% of the values in a normal distribution with a confidence level of 95% and a sample size of 385 is:
tolerance interval = mean +/- 1.96 * (1 / √t(385))
This can be simplified to:
tolerance interval = mean +/- 0.10
Therefore, we can say with 95% confidence that at least 90% of the values in a normal distribution fall within the tolerance interval of mean +/- 0.10.
Know more about the standard normal distribution
https://brainly.com/question/4079902
#SPJ11
which is the equivalent of 145.12° written in DMS form?
Answers
Answer:
145° 7' 12"
Step-by-step explanation:
145.12° written in DMS form
145°
0.12 *60 (1 degree = 60 minutes)=7.2 minutes
0.2*60 ( 1 minute=60 sec)=0.2*60=12"
These data sets show the ages of students in two college classes. Class #1: 28,19,21,23,19,24,19,20 Class #2: 18,23,20,18,49,21,25,19 Which class would you expect to have the larger standard deviation in its ages? Explain why. (You may use Excel to calculate the standard deviation, but you still need to use the meaning of standard deviation to explain why the standard deviation of ages in one class is larger than that in the other.)
Answers
The standard deviation measures the spread or dispersion of a dataset. By calculating the standard deviation for both Class #1 and Class #2, it is determined that Class #2 has a larger standard deviation than Class #1.
We must calculate the standard deviation for both classes and compare the results to determine which class would likely have the larger age standard deviation. The spread or dispersion of a dataset is measured by the standard deviation.
Using Excel, let's determine the standard deviation for the two classes:
Class #1: 28, 19, 21, 23, 19, 24, 19, 20
Step 1: Determine the ages' mean (average):
Step 2: The mean is equal to 22.5 (28 - 19 - 21 - 23 - 19 - 24 - 19 - 20). For each age, calculate the squared difference from the mean:
(28 - 22.5)^2 = 30.25
(19 - 22.5)^2 = 12.25
(21 - 22.5)^2 = 2.25
(23 - 22.5)^2 = 0.25
(19 - 22.5)^2 = 12.25
(24 - 22.5)^2 = 2.25
(19 - 22.5)^2 = 12.25
(20 - 22.5)^2 = 6.25
Step 3: Sum the squared differences and divide by the number of ages to determine the variance:
The variance is equal to 10.9375 times 8 (32.25 times 12.25 times 2.25 times 12.25 times 6.25). To get the standard deviation, take the square root of the variance:
The standard deviation for Class #2 can be calculated as follows: Standard Deviation = (10.9375) 3.307 18, 23, 20, 18, 49, 21, 25, 19
Step 1: Determine the ages' mean (average):
Mean = (23.875) / 8 = (18 + 23 + 20 + 18 + 49 + 21 + 25 + 19) Step 2: For each age, calculate the squared difference from the mean:
(18 - 23.875)^2 ≈ 34.816
(23 - 23.875)^2 ≈ 0.756
(20 - 23.875)^2 ≈ 14.616
(18 - 23.875)^2 ≈ 34.816
(49 - 23.875)^2 ≈ 640.641
(21 - 23.875)^2 ≈ 8.316
(25 - 23.875)^2 ≈ 1.316
(19 - 23.875)^2 ≈ 22.816
Step 3: Sum the squared differences and divide by the number of ages to determine the variance:
Variance is equal to (34.816, 0.756, 14.616, 34.816, 640.641, 8.316, 1.316, and 22.816) / 8 99.084. To get the standard deviation, take the square root of the variance:
According to the calculations, Class #2 has a standard deviation that is approximately 9.953 higher than that of Class #1 (approximately 3.307).
The standard deviation estimates how much the ages in each class go amiss from the mean. When compared to Class 1, a higher standard deviation indicates that the ages in Class #2 are more dispersed or varied. That is to say, whereas the ages in Class #1 are somewhat closer to the mean, those in Class #2 have a wider range and are more dispersed from the average age.
This could imply that Class #2 has a wider age range, possibly including outliers like the student who is 49 years old, which contributes to the higher standard deviation. On the other hand, Class #1 has ages that are more closely related to the mean and have a smaller standard deviation.
To know more about Standard deviation, visit
brainly.com/question/475676
#SPJ11
How can multiplying integers be used in the real world???
Answers
Answer:
Multiplying Integers can be used in the real world in a lot of ways because of their positive and negative. The Positive and Negative will be used as like what you have to owe in money/cash or what you have.
Step-by-step explanation:
Hopes This Helps
LOOK OMG :0
Jennifer is a wedding planner. She set up six chairs at each table for the reception. If t represents the number of tables, which of the following expressions represents the total number of chairs that she set up?
A. 6 + t
B. t + 6
C. 6t
D. t - 6 ( hurry fo meh)
Answers
For every table that is present there are 6 chairs at the table
Answer:
C is the correct answer
solve for x and y pls and thank u

Answers
Answer:
fourth
Step-by-step explanation:
Angle X is the inscribed angle of the two arcs that measure 122 and 64 so
\(x = \frac{1}{2} (122 + 64)\)
\(x = \frac{1}{2} (186) = 93\)
A cyclic quadrilateral states that the opposite angles add up to 180
so
\(y = 18 0 - 83 = 97\)
The correct answer is the fourth option
Soccer ball profit
y=-6x^2 + 100x - 180
Suppose the store wants to earn a daily profit of $150 from the sale of soccer balls. To earn this profit, what price should the store charge for each soccer ball? Explain how to solve this problem.
Answers
Answer:
$8.33 per soccer ball.
Step-by-step explanation:
Y max is =236.67 is the max profit from the soccer balls. This goes on when you charge 8.33 a ball
Answer:
need to solve the equation 150 = -6x2 + 100x - 180. I can subtract 150 from both sides and use the quadratic formula to find x = 4.53 and 12.13. This means that if the store sells soccer balls for $4.53 or $12.13, it will earn a daily profit of $150.
Evaluate the function: f(x)=x2+2x, find f(−1)
Answers
Answer:
\(f( - 1) = - 1\)
Step-by-step explanation:
\(f(x) = {x}^{2} + 2x\)
Substitute x = -1 in the equation.
\(f( - 1) = {( - 1)}^{2} + 2( - 1) \\ f( - 1) = 1 - 2 \\ f( - 1) = - 1\)
One cantaloupe costs $2. How many
cantaloupes can you buy for $6?
Answers
Answer:
3
Step-by-step explanation:
ignore this i need more letters lol have a good day
Answer:
You could buy 3 cantaloupes.
Step-by-step explanation:
So, you have $6. Now, what we would do is (O is 1 cantaloupe):
If O cost $2, do the following:
O O O O O
2 2 2 2 2
Now, lets count up til we get 6:
2 + 2 = 4; 4 + 2 = 6;
After you have done that step, count how many 2's you see in that equation. I see 3.
Therefore, you could buy 3 cantaloupes.
Evaluate : (12.5)³
find the answer
Answers
Answer:
1953.125
Step-by-step explanation:
(12.5)³
= 12.5 × 12.5 × 12.5
= 1953.125
Answer: 1953.125
(12.5)³
so 12.5 multiplied to itself thrice
12.5x12.5x12.5
which is 1953.125
What is the least common
multiple of 15a² and 3a2?
1.3a2
2.3a3
3.15a2
4.15a3
Answers
Answer:
1. 3a2
Step-by-step explanation:
20. Mercury 203 has a decay rate of 1.481% per day. Given the exponential model representing the amount of Mercury 203 remaining after days, find how long it will take 300 grams of the Mercury 203 to
Answers
According to the model, it will take 0 days for 300 grams of Mercury 203 to completely decay.
The natural logarithm, often denoted as ln(x), is a mathematical function that represents the logarithm to the base e, where e is the mathematical constant approximately equal to 2.71828.
To find out how long it will take for 300 grams of Mercury 203 to decay, we can use the exponential decay model.
The general formula for exponential decay is given by:
A(t) = A₀ * e^(-rt),
where A(t) represents the amount of the substance at time t, A₀ is the initial amount, r is the decay rate, and e is the base of the natural logarithm.
In this case, we have the initial amount A₀ = 300 grams and the decay rate r = 0.01481 (1.481% written as a decimal).
We want to find the time t when the amount A(t) is equal to zero. Substituting these values into the formula, we have:
0 = 300 * e^(-0.01481t).
To solve for t, we can divide both sides of the equation by 300 and take the natural logarithm of both sides:
ln(0) = ln(e^(-0.01481t)),
0 = -0.01481t.
To isolate t, we divide both sides by -0.01481:
0 / -0.01481 = t,
t = 0.
Therefore, according to the model, it will take 0 days for 300 grams of Mercury 203 to completely decay.
To know more about exponential decay, visit:
https://brainly.com/question/2311769
#SPJ11
Can anyone help with this? I'm having some trouble.

Answers
70x = 360
X = 5.14
Question 10 of 25
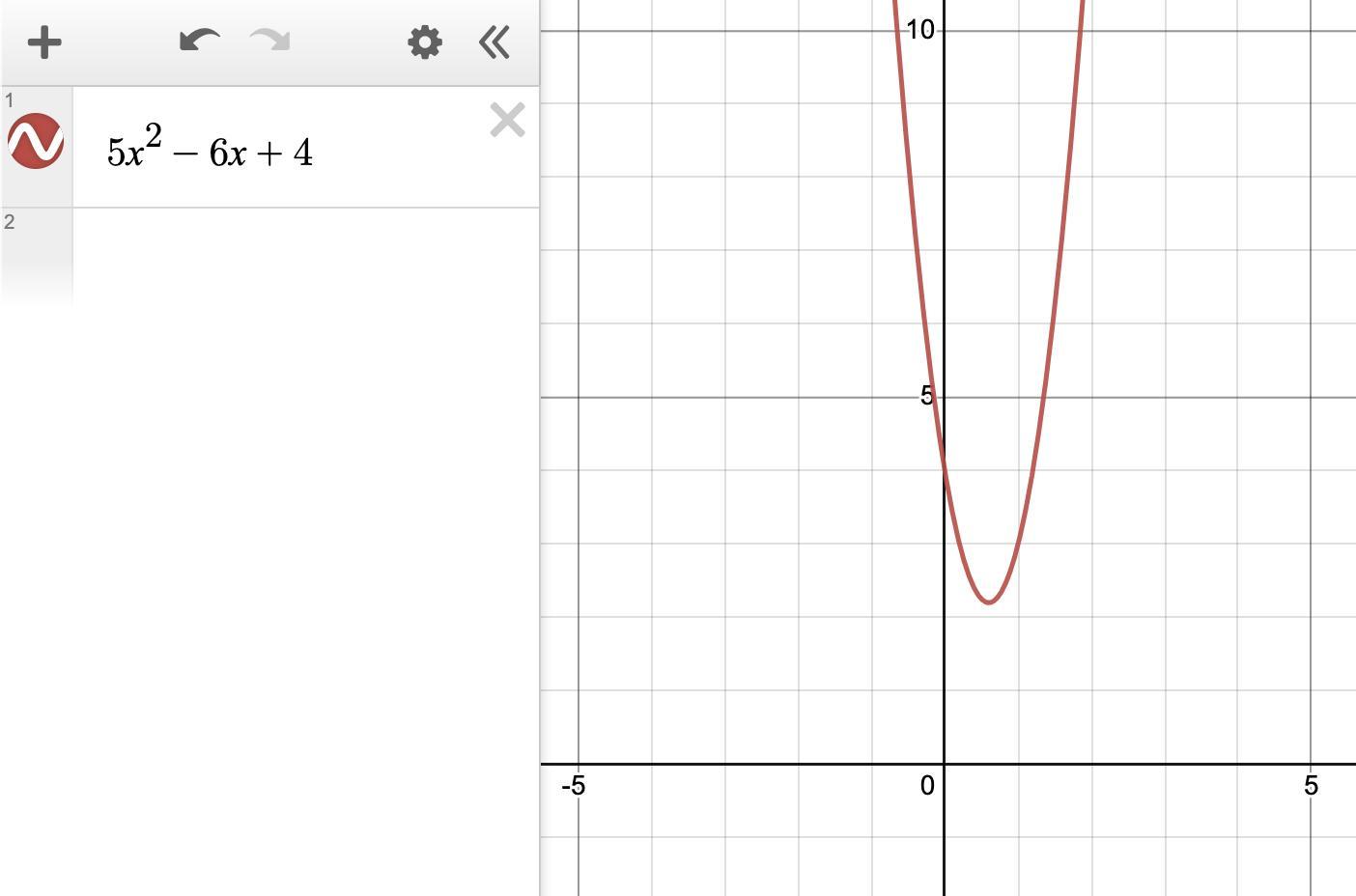
The polynomial (x-2) is a factor of the polynomial 5x² - 6x +4.
O A. True
OB. False
Answers
Answer:
B. False
Step-by-step explanation:
5x² - 6x + 4 | 5 × 4 = 20
Can't factor it normally
√b² - 4ac
-b ± ---------------
2a
√(-6)² - 4(5)(4)
-(-6) ± ---------------
2(5)
√36 - 80
6 ± ---------------
10
6 ± √-44
---------------
10
6 ± √-4 × 11
---------------
10
6 ± 2i√11
---------------
10
The answer is actually
3 ± i√11
---------------
5
I hope this helps!
Answer:
B. False
Step-by-step explanation:
You want to know if (x -2) is a factor of 5x² -6x +4.
RemainderThere are a couple of ways you can determine whether (x -2) is a factor. One is to look at the polynomial value at x=2:
5x² -6x +4 = (5x -6)x +4 = (5(2) -6)(2) +4 = 4(2) +4 = 12
The value is not 0, so (x -2) is not a factor.
Other factorAnother way to tell is to determine what the other factor would be.
The product of roots is the ratio c/a = 4/5 in the polynomial. If 2 is a root, then (4/5)/2 = 2/5 is the other root. That would mean the factorization of the polynomial is ...
(5x -2)(x -2) = 5x² -12x +4 . . . . . . not the same polynomial
The polynomial 5x² -6x +4 does not have a factor (x -2).
GraphThe graph of the polynomial has no x-intercepts, so (x -2) cannot be a factor.
which is true about the sampling distribution? group of answer choices the sampling distribution is the distribution of values that we observe in the sample we have taken from the population the sampling distribution of a statistic is for a hypothetical scenario, we don't actually observe it in practice---we only observe one sample in practice. the sampling distribution of every statistic (mean, median, variance, difference between two means, etc.) has the same shape. the sampling distribution of a statistic is a distribution that we should approximate in practice by taking many small samples.
Answers
The true statement about the sampling distribution is "the sampling distribution of a statistic is a distribution that we should approximate in exercise by taking many small samples."
The sampling distribution is the theoretical distribution of a statistic (including the imply, median, or variance) based totally on all viable samples of a given size that could be taken from a population. it is a beneficial idea in statistics as it allows us to make inferences approximately the populace based on records gathered from a pattern.
In practice, we can not examine the whole sampling distribution, as it's far based totally on all viable samples, which isn't always feasible to gain. but, we will approximate the sampling distribution by taking many small samples from the population and calculating the applicable statistic for every sample.
Because the variety of samples increases, the distribution of these data will converge to the sampling distribution, allowing us to make more accurate inferences approximately the population.
Learn more about Sampling distribution:-
https://brainly.com/question/30331609
#SPJ4
On the coordinate plane below, quadrilateral 1 has been transformed to form quadrilateral 2 which if these could be the transformation choose all that are correct
Answers
Answer:
I think the answer is A reflection across the line y=1 and A reflection across the y-axis and then a translation 2 units to the right
Step-by-step explanation:
I’m not sure if this is the answer but I want to help out as much as possible
Answer:b
Step-by-step explanation: