Let S={[8 -2 6+ ]: ab oed} a, (a) Prove that S is a subspace of Mus(R) by verifying that S is closed under addition and closed under scalar multiplication (b) Find a basis fo?
Answers
(a) To prove that S is a subspace of M₃(R), we need to verify that S is closed under addition and closed under scalar multiplication.
Closure under addition:
Let A, B be two matrices in S. We have A = [8 -2 6] and B = [a b c]. To show closure under addition, we need to prove that A + B is also in S.
A + B = [8 -2 6] + [a b c] = [8 + a -2 + b 6 + c]
Since a, b, c are arbitrary real numbers, the sum of the corresponding entries 8 + a, -2 + b, and 6 + c can be any real number. Therefore, A + B is of the form [8 + a' -2 + b' 6 + c'], where a', b', c' are real numbers.
Thus, A + B is an element of S. Therefore, S is closed under addition.
Closure under scalar multiplication:
Let A be a matrix in S and k be a scalar. We have A = [8 -2 6]. To show closure under scalar multiplication, we need to prove that kA is also in S.
kA = k[8 -2 6] = [k(8) k(-2) k(6)] = [8k -2k 6k]
Since k is a scalar, 8k, -2k, and 6k are real numbers. Therefore, kA is of the form [8k -2k 6k], where k' is a real number.
Thus, kA is an element of S. Therefore, S is closed under scalar multiplication.
Since S satisfies both closure under addition and closure under scalar multiplication, we can conclude that S is a subspace of M₃(R).
(b) To find a basis for S, we need to find a set of linearly independent vectors that span S.
The matrix A = [8 -2 6] is already an element of S. We can observe that this matrix has no zero entries, which implies linear independence.
Therefore, the set {A} = {[8 -2 6]} forms a basis for S.
To know more about subspaces and basis, refer here:
https://brainly.com/question/31971747#
#SPJ11
Related Questions
in 2021, the national highway traffic administration said that, based on survey data, 84% of drivers use seat belts regularly. if four drivers are randomly selected, what is the probability that at least one of them is not wearing a seatbelt?
Answers
The probability that at least one of them is not wearing a seatbelt is 0.5021.
What is meant by probability?Potential is described by probability. The value's range is 0 to 1. Probability has been applied into mathematics to predict the likelihood of events. Probability is a branch of mathematics that deals with numerical representations of the likelihood of an event occurring or of a proposition being true.
These concepts now have an axiomatic mathematical formalization thanks to probability theory, which is widely employed in disciplines including statistics, mathematics, science, finance, gambling, artificial intelligence, machine learning, computer science, and philosophy.
Let X be the proportion of drivers who do not use a seat belt. It has a binomial distribution, as shown by,
n=4, p=1-0.84
p=0.16
The likelihood that at least one of them is not wearing seatbelt is:
P(X≥1)=1-P(X<1)
=1-P(X=0)
=1-{(4₀)(0.16)⁰(1-0.16)⁴⁻⁰
=1-0.4979
=0.5021.
Therefore, the probability that at least one of them is not wearing a seatbelt is 0.5021.
To know more about probability, visit:
https://brainly.com/question/15124899
#SPJ1
When an ice cream shop was founded, it made 22 different flavors of ice cream. If you had a choice of having a single flavor of ice cream in a cone, a cup, or a sundae, how many different desserts could you have
Answers
There are 275 different desserts at this ice cream shop.
If the ice cream shop made 22 different flavors of ice cream, you would have 22 choices for a single flavor in a cone or a cup. For a sundae, you could choose a combination of two or more flavors. Let's assume you choose two flavors for your sundae.
You would have 22 options for the first flavor and 21 options for the second flavor since you can't repeat the same flavor.
So, the total number of different desserts you could have is:
22 (single flavor in a cone) + 22 (single flavor in a cup) +\(22 (\frac{21}{2} )\) (two flavors in a sundae)
= 22 + 22 + 231
= 275
Therefore, you could have 275 different desserts at this ice cream shop.
To know more about "Combination" refer here:
https://brainly.com/question/20211959#
#SPJ11
Consider a clock with an hour hand and minute hand. What is the measure of the angle the minute hand traces in 20 minutes?
Answers
The measure of the angle the minute hand traces in 20 minutes is 120 degrees.
In a clock, the minute hand completes a full revolution every 60 minutes, which is 360 degrees. Therefore, in 1 minute, the minute hand covers 360 degrees / 60 minutes = 6 degrees.
To find the measure of the angle the minute hand traces in 20 minutes, we can multiply the rate per minute (6 degrees) by the number of minutes:
Angle traced by minute hand = Rate per minute × Number of minutes
Angle traced by minute hand = 6 degrees/minute × 20 minutes
Angle traced by minute hand = 120 degrees
Therefore, the measure of the angle the minute hand traces in 20 minutes is 120 degrees.
For more details about clock
https://brainly.com/question/29144726
#SPJ4
AC and BE intersect at point P. If m∠APE = 70°, then what is the measure of m∠EPD?

Answers
The angles m∠APE and m∠EPD are complementary angles and so the measure of angle m∠EPD is equal to 20° which makes option D correct.
What are complementary anglesIn geometry, if two angles are said to be complementary, then the total of their sum is equal to 90°.
The angles m∠APE and m∠EPD are complementary angles so we evaluate for the angle m∠EPD as follows:
m∠APE + m∠EPD = 90°
70° + m∠EPD = 90°
m∠EPD = 90° - 70° {subtract 70° from both sides}
m∠EPD = 20°.
Therefore, the measure of angle m∠EPD is equal to 20°.
Know more about complementary angles here:https://brainly.com/question/98924
#SPJ1
What is the solution to the equation 9(x − 2) = 27? (1 point) x = 2.5 x = 0.5 x = −0.5 x = 3.5
Answers
Answer:
x = 5
Step-by-step explanation:
9(x - 2) = 27
9x - 18 = 27
+18 +18
9x = 45
/9 /9
x = 5
Urgent!!! PLease answer and help me!! 50 Points!!!

Answers
Answer:
11.6 is right
Step-by-step explanation:
which number comes next in this series 8, 4, 2, 1=5 25
Answers
The next number in the series is 125.
The given series appears to follow a pattern of dividing each number by 2 and then subtracting 1 to obtain the next number. Let's analyze the pattern step by step:
Starting with 8, when we divide it by 2, we get 4. Then subtracting 1 from 4 gives us 3, which is not part of the given series. However, if we continue the pattern, dividing 4 by 2 gives us 2, and subtracting 1 from 2 gives us 1, which matches the next number in the series.
Moving forward, if we divide 2 by 2, we get 1, and subtracting 1 from 1 gives us 0. However, 0 is not part of the given series. If we continue the pattern, dividing 1 by 2 gives us 0.5, and subtracting 1 from 0.5 gives us -0.5. Again, -0.5 is not part of the series.
Therefore, it seems reasonable to consider that the pattern is only valid when the result of the division is a whole number. Following this pattern, if we divide 1 by 2, we obtain 0.5, and subtracting 1 from 0.5 gives us -0.5. However, if we divide 0.5 by 2, we get 0.25, and subtracting 1 from 0.25 gives us -0.75. Therefore, we conclude that the pattern breaks down after reaching 1.
Taking into account the valid results of the pattern, the next number in the series would be obtained by dividing 1 by 2, which gives us 0.5, and then subtracting 1 from 0.5, resulting in -0.5. However, since negative numbers are not part of the given series, we disregard this result.
Considering that the pattern breaks down after reaching 1, we cannot determine the next number based on the given pattern. Therefore, the given series does not follow a consistent pattern, making it impossible to identify the next number accurately.
Learn more about series here:
https://brainly.com/question/30457228
#SPJ11
can someone please help with this geometry

Answers
Answer:
∠ABD = 19.5°
∠ABE = 160.5°
Step-by-step explanation:
Given angle ABC = 39° and its bisector BD, you want the measures of angle ABD and ABE, its supplement.
Angle bisectorAn angle bisector divides an angle into two equal parts, each with half the measure of the whole.
∠ABD = 1/2∠ABC
∠ABD = 1/2(39°)
∠ABD = 19.5°
Linear pairThe angles of a linear pair are supplementary: they total 180°. Angles ABD and ABE form a linear pair.
∠ABE = 180° -∠ABD
∠ABE = 180° -19.5°
∠ABE = 160.5°
Given f(x), which function is the inverse?
f(x) = 3x - 5
A) g(y) = 3y + 5
B) g(y) = // +5
C) g(y) = 3+5 3
D) g(y) = 5y 3
Answers
Answer:
g(y) = 1/3y + 5/3
Step-by-step Explanation:
We know that f(x) is synonymous with y so we can rewrite f(x) as y = 3x -5
To find the inverse of the function, we can switch y with x and x with y:
x = 3y - 5
Now we can isolate y to find the inverse of f(x):
(x = 3y - 5) + 5
(x + 5 = 3y) / 3
x/3 + 5/3 = y
1/3x + 5/3 = y
Thus, the inverse of f(x) is f^-1(x) = 1/3x + 5/3. Since we want to write the inverse in terms of y, we get g(y) = 1/3y + 5/3.
If this answer doesn't match your answer choices (some of the answer choices you provided are unclear), please attach a pic and I can help you figure out which answer choice is correct)
1.)Combine like terms: 3(7n+6)-5n
Answers
Hey there!
3(7n + 6) - 5n
= 3(7n) + 3(6) - 5n
= 21n + 18 - 5n
= 16n + 18
Therefore, your answer should be:
16n + 18
Good luck on your assignment & enjoy your day!
~Amphitrite1040:)
here is my question

Answers
Answer:
It represents a linear function because there is a constant rate of change.
Step-by-step explanation:
A linear function is arranged in or extending along a straight or nearly straight line.
So if the numbers keeps increasing, which it is, it will be rising in an almost complete straight line on a graph. That means it is a linear function because the numbers keep increasing.
Find the measure of each angle

Answers
Answer:
1 = 44° (Opposite angles>
2 = 77° (By Angle sum property of a triangle)
3 = 82° ('' '' ' '' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ''')
a number from 100 to 999 incluese is chosen at random what is the probability that it contains no 0's
Answers
The probability that it contains no 0's is 0.19%
What is Probability?
The area of mathematics known as probability deals with numerical representations of the likelihood that an event will occur or that a statement is true. An event's probability is a number between 0 and 1, where, roughly speaking, 0 denotes the event's impossibility and 1 denotes certainty. The chances that an event will occur increases with its probability.
Total number of integer from 100 to 999 where both are included = 900
Now, from 100- 999 inclusive there are 19 numbers containing at least zero
(100,101,102,103,104,105,106,107,108,109,110,120,130,140,150,160,170,180,
190)
and we have the same number in each hundred from x00 to x99 where x ranges from 1 to 9
so, the total number of integer from 100 - 999 inclusive that have zero = 9 (19) = 171
Hence, the probability that we select a digit that contain zero
= 171/900
= 19/100
=0.19%
The probability that it contains no 0's randomly is 0.19%
To learn more about Probability visit:
brainly.com/question/29381779
#SPJ4
Mr. Carandang sold a total of 1,790 prints of one of his drawings. Out of all 1,273 unframed prints that he sold, 152 were small and 544 were medium-sized. Out of all of the framed prints that he sold, 23 were small and 42 were extra large. Of the large prints that he sold, 188 were framed and 496 were unframed.
Small Medium Large Extra Large Total
Framed 23 264 188 42 ?
Unframed 152 544 496 81 1,273
Total 175 808 684 123 1,790
How many framed prints did Mr. Carandang sell?
329
475
517
1,034
Answers
Answer:
Total framed print = 517
Step-by-step explanation:
Framed print:
Small = 23
Medium = 264
Large = 188
Extra large = 42
Total framed print = Small + Medium + Large + extra large
= 23 + 264 + 188 + 42
= 517
Total framed print = 517
Unframed print:
Small = 152
Medium = 544
Large = 496
Extra large = 81
Total unframed print= Small + Medium + Large + extra large
= 152 + 544 + 496 + 81
= 1,273
Answer:
C- 517
Step-by-step explanation:
In a survey of 1,400 people who owned a certain type of car, 900 said they would buy that type of car again. What percent of the people surveyed were satisfied with the car?
Answers
Answer:
about 64.29%
Step-by-step explanation:
900/1400= 0.64285...
=about 64.29%
Subtract the sum of -4/7 and -5/7 from the sum of 1/2 and -21/22
Answers
The value of the fraction -5/7 and -4/7 added and subtracted from the fraction -21/2 added to 1/22 is 64/77.
The sum of 1/2 and -21/22 can be found by finding a common denominator,
1/2 = 11/22 (since 11 x 2 = 22)
-21/22 = -21/22
Therefore, the sum of 1/2 and -21/22 is,
= 11/22 - 21/22
= -10/22 = -5/11
The sum of -4/7 and -5/7 is,
-4/7 - 5/7 = -9/7
Now, subtracting as asked in the question.
= (-5/11)-(-9/7)
= (-5/11)+(9/7)
Finding common denominator to add the fractions,
7 x 11 = 77
(-5x7)/(11x7)+(9x11)/(7x11)
= -35/77 + 99/77
Now, we can combine the numerators,
-35/77 + 99/77 = 64/77
Therefore, the final answer is 64/77.
To know more about common denominator, visit,
https://brainly.com/question/19249494
#SPJ4
suppose you get a cash prize of $100 if you win a game. the probability of winning the game is 0.7. what is the probability of winning $600 or less if you play the game 10 times, assuming that each game is independent?
Answers
The probability of winning $600 or less if you play the game 10 times, assuming that each game is independent IS 0.5630.
Define binomial distribution.A popular probability distribution known as the binomial distribution simulates the likelihood of getting one of two outcomes given a set of parameters. It totals the number of trials when each trial has an equal chance of producing a particular result. The probability of success raised to the power of the number of successes and the probability of failure raised to the power of the difference between the number of successes and the number of trials are multiplied to create the binomial distribution.
Given,
Cash prize = $100
Probability of winning the game = 0.7
Using binomial distribution,
P(4 ≤X≤ 6) = P( X = 4) + P( X = 5) + P( X = 6)
P( 4 ≤ X ≤ 6)
= 1/4(0.6)⁴(0.4)⁴ + 10/5 (0.6)⁵(0.4)⁵ + 10/6 (0.6)⁶(0.4)⁶
= 0.1115 + 0.2007 + 0.2508
= 0.5630
The probability of winning $600 or less if you play the game 10 times, assuming that each game is independent IS 0.5630.
To learn more about binomial distribution, visit:
https://brainly.com/question/16759552
#SPJ4
A cylinder was removed from the inside of another cylinder to form the solid below.
Which is the closest to the volume of the solid that remained?
2286 cubic inches
3266 cubic inches
10,864 cubic inches
13,062 cubic inches

Answers
Please answer fast!!!!!
Explain the steps you would use to solve the equation. Find the solution.
8^2x=4096
Answers
Answer:
x = 2
Step-by-step explanation:
note that 4096 = \(8^{4}\) , then
\(8^{2x}\) = \(8^{4}\)
Since bases on both sides are equal, both 8 , then equate the exponents
2x = 4 ( divide both sides by 2 )
x = 2
Answer:
x = 2
Step-by-step explanation:
\(8^{2x} = 4096\)
Step 1 :- Write 4096 in the exponential form with the base of 8.
\(8^{2x} = 8^4 \)
Step 2 :- Since the base of both equation is same , set the exponents equal.
2x = 4
Step 3 :- Divide both side by 2
\({2x}{2} = \frac{4 }{2}\)
x = 2
The question I have is y=3bx-7x. It says to solve the literal equation for x.
Answers
Answer:
y/( 3b-7)=x
Step-by-step explanation:
y=3bx-7x
Factor out x
y=(3b-7)x
Divide each side by (3b-7)
y/( 3b-7)=(3b-7)x/ ( 3b-7)
y/( 3b-7)=x
Answer:
\(\huge \boxed{x= \frac{y}{3b-7} }\)
Step-by-step explanation:
\(\sf y=3bx-7x\)
Factor out x from the expression.
\(\sf y=x(3b-7)\)
Divide both sides by (3b - 7).
\(\sf \displaystyle \frac{y}{3b-7} =x\)
Find the values of the variables for the parallelogram.
mZ1 = 5y – 20
X=
Y=
Z=
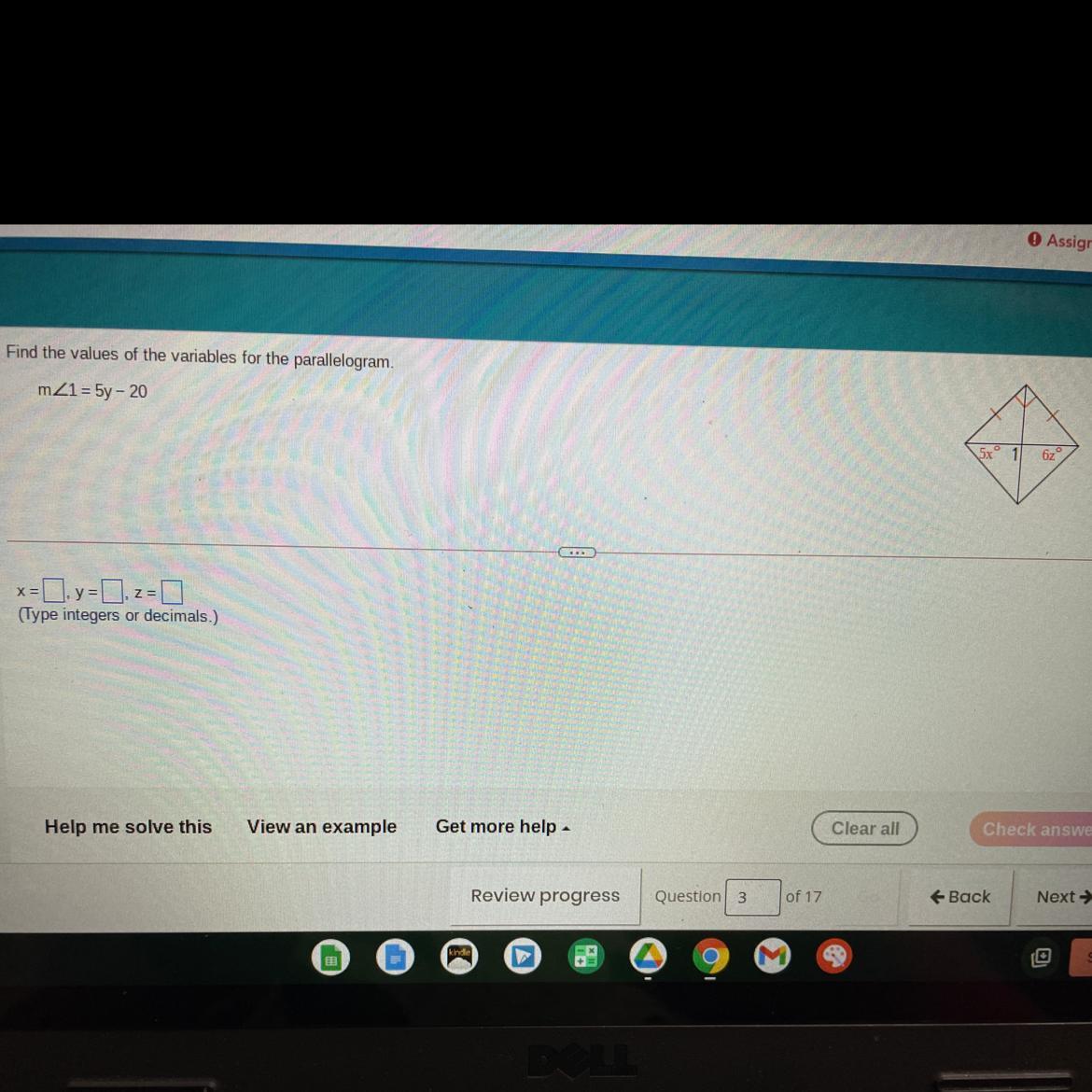
Answers
Answer:
Step-by-step explanation:

G = {(1, 1), (1, 2), (1, 3), (1, 4)} Is G a function and why?
Answers
Answer:
\(G\) is not function. The reason is that it is not one-to-one.
Step-by-step explanation:
A function is a mapping that is also one-to-one.
\(G\) is indeed a mapping; it takes an input and relates it to one or more outputs.
Input: \(1\), output: Input: \(1\), output: \(2\).Input: \(1\), output: \(3\).Input: \(1\), output: \(4\).A mapping is one-to-one if and only if each input is mapped to only one output. \(G\) is not one-to-one because it maps the input \(1\) to four different outputs. Hence, \(G\) isn't a function.
please help me answer

Answers
Answer:
9
Step-by-step explanation:
Because x = 2 we can re arrange this too 3x2^2 - 2x2 + 1
after doing this we can simplify it too 12-4+1 which when we do it is just 9.
2 [x² + 2x + 1] - x²-4x+4 = x²-3x
Answers
The solution for the equation given would be x = 2 and x = -1.
How to find the solution to the equation?To solve the equation 2[x² + 2x + 1] - x² - 4x + 4 = x² - 3x, we can simplify and rearrange the terms as follows:
2x² + 4x + 2 - x² - 4x + 4 = x² - 3x
x² - 3x + 6 = x² - 3x
2x² - 2x - 6 = 0
Dividing both sides by 2, we get:
x² - x - 3 = 0
We can then solve for x by factoring or using the quadratic formula. Factoring gives:
(x - 2)(x + 1) = 0
So, the solutions are x = 2 and x = -1.
Find out more on equations at https://brainly.com/question/30164833
#SPJ1
1252
Which expression is equivalent to
?
3
125
25
O
10
10
O 10
O 25

Answers
The solution is, the value of the given expression is equivalent to 25.
What is an exponent in math?An exponent refers to the number of times a number is multiplied by itself. For example, 2 to the 3rd (written like this: 23) means: 2 x 2 x 2 = 8. 23 is not the same as 2 x 3 = 6. Remember that a number raised to the power of 1 is itself.
here, we have,
given that,
the given expression is
125^2/ 125^(4/3)
=125^2/ 5^4
=125*125/5*5*5*5
=25*5*25*5/5*5*5*5
=25*25/ 5*5
=5*5
=25
so, we get the value of the given expression is equivalent to 25.
To learn more on exponent number click:
brainly.com/question/19467739
#SPJ7
according to a previous study, the average height of kennesaw state university students was 68 inches in fall 2005. we are curious about whether the average height of ksu students has changed since 2005. we measure the heights of 50 randomly selected students and find a sample mean of 69.1 inches and sample standard deviation of 3.5 inches. conduct a hypothesis test at a significance level of 0.05 to determine if the height of ksu students has changed since 2005. what is the p-value of the test?
Answers
Based on the calculated test statistic and the degrees of freedom, you can find the p-value associated with the test statistic.
To determine if the average height of Kennesaw State University (KSU) students has changed since 2005, we can conduct a hypothesis test.
Here are the steps to perform the test:
1. Set up the null and alternative hypotheses:
- Null hypothesis (H0): The average height of KSU students has not changed since 2005.
- Alternative hypothesis (Ha): The average height of KSU students has changed since 2005.
2. Determine the test statistic:
- We will use a t-test since we have a sample mean and standard deviation.
3. Calculate the test statistic:
- Test statistic = (sample mean - population mean) / (sample standard deviation / √sample size)
- In this case, the sample mean is 69.1 inches, the population mean (from 2005) is 68 inches, the sample standard deviation is 3.5 inches, and the sample size is 50.
4. Determine the p-value:
- The p-value is the probability of obtaining a test statistic as extreme as the one calculated, assuming the null hypothesis is true.
- Using the t-distribution and the degrees of freedom (n-1), we can calculate the p-value associated with the test statistic.
5. Compare the p-value to the significance level:
- In this case, the significance level is 0.05 (or 5%).
- If the p-value is less than 0.05, we reject the null hypothesis and conclude that the average height of KSU students has changed since 2005. Otherwise, we fail to reject the null hypothesis.
Learn more about p-value from the link:
https://brainly.com/question/13786078
#SPJ11
Has the marrying age of a man changed over the years? The United States Bureau of the Census takes a formal count of everyone in the U.S. every 10 years and has provided the following data that gives the median age of an American man at the time of his first marriage.
Year
1910
1920
1930
1940
1950
1960
1970
1980
1990
2000
Median Age
25.1
24.6
24.3
24.3
22.8
22.8
23.2
24.7
26.1
26.8
Determine the average rate of change in median age per year from 1930 to 1960.
a.
-0.5 years of age per year
b.
20 years of age per year
c.
-0.05 years of age per year
d.
+0.05 years of age per year
Answers
-0.05 is the average rate of change in median age per year from 1930 to 1960.
What is ratio?The ratio can be defined as the number that can be used to represent one quantity as a percentage of another. Only when the two numbers in a ratio have the same unit can they be compared. Ratios are used to compare two objects.
Given, a data set that gives the median age of an American man at the time of his first marriage.
Year Median age
1910 25.1
1920 24.6
1930 24.3
1940 24.3
1950 22.8
1960 22.8
1970 23.2
1980 24.7
1990 26.1
2000 26.8
The average rate of change from 1930 to 1960 = (-24.3 + 22.8) / (1960-1930)
The average rate of change from 1930 to 1960 = -0.05
Therefore, the average rate of change in median age per year from 1930 to 1960 is -0.05.
Learn more about ratios here:
https://brainly.com/question/13419413
#SPJ1
Express the formula d=rt in terms of the time,t. Use your formula to find the time when the distance is 40 and the rate is 8.
Answers
The expression for d=rt in terms of the time is t = d/r; t = 5.
What is time? Time can be defined as a continuous and ongoing sequence of events that occur consecutively from the past to the present to the future. Time is used to measure, measure or compare the duration of events or the intervals between them, and even the sequence of events. Time is a useful concept that we use in our daily life. We have to watch when we cook, play, study, go to school, meet someone, etc. So knowing the right time is very important. Time is usually the answer to when an event happens or happened. The concept of time determines when a certain event occurs, has occurred or will occur. Time is a measurable quantity and is also infinite. The time is calculated in seconds, minutes, hours, days, months and years.Therefore,
In the equation d=rt
t = d/r
when distance is 40 and the rate is 8
t = d/r
Replace d with 40 and rate with 8
t = 40/8
t = 5
To learn more about time, refer;
https://brainly.com/question/28050940
#SPJ1
Please help me I am really confused and need help with this.

Answers
Answer:
Step-by-step explanation:
y=10
the list shows the weight in pounds of 6 puppies at birth. 3, 1.6, 2.8, 2.5, 1.7, 2.8 what is the mean absolute deviation of these numbers?
Answers
Step 1: Find the mean (average) of the numbers.
Mean = (3 + 1.6 + 2.8 + 2.5 + 1.7 + 2.8) / 6 = 2.3667 (rounded to 4 decimal places)
Step 2: Find the absolute deviation of each number by subtracting the mean from each number and taking the absolute value.
|3 - 2.3667| = 0.6333
|1.6 - 2.3667| = 0.7667
|2.8 - 2.3667| = 0.4333
|2.5 - 2.3667| = 0.1333
|1.7 - 2.3667| = 0.6667
|2.8 - 2.3667| = 0.4333
Step 3: Find the mean of the absolute deviations.
MAD = (0.6333 + 0.7667 + 0.4333 + 0.1333 + 0.6667 + 0.4333) / 6
MAD = 0.5 (rounded to 1 decimal place)
Therefore, the mean absolute deviation of the given set of numbers is 0.5.