Listed below are the numbers of cricket chirps in 1 minute and the corresponding temperatures in F. Find the regression equation, letting chirps in 1 minute be the independent (x) variable. Find the best predicted temperature at a time when a cricket chirps times in 1 minute, using the regression equation. What is wrong with this predicted temperature?
Chirps in 1 Min: 834, 1041, 904, 948, 1100, 1174, 1201, 1000
Temperature in Degree F: 70.5, 80.8, 76.1, 76.7, 85.6, 84.4, 89.9, 76.9
Answers
The predicted temperature at a given number of cricket chirps per minute is 82.03 degrees F, assuming a linear relationship.
The predicted temperature at a given number of cricket chirps per minute using the regression equation is 82.03 degrees F.
The problem with this predicted temperature is that it assumes a linear relationship between the number of chirps and temperature, which may not be accurate or valid in this case.
To find the regression equation, we can use linear regression analysis. Using the given data, we can calculate the regression line that best fits the relationship between chirps and temperature. The regression equation has the form:
Temperature = a + b * Chirps
By performing the regression analysis, we can find the values of the regression coefficients 'a' and 'b'. The regression equation for this data set is:
Temperature = 22.85 + 0.079 * Chirps
Using this equation, we can estimate the temperature at a given number of chirps per minute.
However, it is important to note that the predicted temperature may not be accurate if the relationship between chirps and temperature is not truly linear or if there are other factors influencing the temperature.
Therefore, the predicted temperature should be interpreted with caution and additional analysis may be needed to validate the relationship between chirps and temperature.
To learn more about linear relationship click here
brainly.com/question/29066440
#SPJ11
Related Questions
the hexagonal prism below has a height of 4 units and a volume of 98 units^3 . find the area of one of its bases.
Answers
The area of one of the bases of the hexagonal prism is approximately 7.39 units^2.
To solve this problem, we can use the formula for the volume of a hexagonal prism:
V = (3√3/2) * a^2 * h
where V is the volume, a is the length of one side of the hexagonal base, and h is the height of the prism.
We are given that the height of the prism is 4 units and the volume is 98 units^3. Plugging these values into the formula, we can solve for the length of one side of the base:
98 = (3√3/2) * a^2 * 4
a^2 = 98 / (12√3)
a ≈ 2.95
Now that we know the length of one side of the base, we can find the area of the hexagon by using the formula:
A = (3√3/2) * a^2
where A is the area of one of the bases. Plugging in the value we found for a, we get:
A = (3√3/2) * (2.95)^2
A ≈ 7.39
Therefore, the area of one of the bases of the hexagonal prism is approximately 7.39 units^2.
To know more about hexagonal prism visit:
https://brainly.com/question/10726499
#SPJ11
10x + 8 = 3(x - 2)
10x + 8 = 3x
Answers
Answer:
1) -2
2) 8/7
Step-by-step explanation:
1) 10x+8=3(x-2)
10x+8=3x-6
10x-3x=-6-8
7x=-14
x=-2
2) 10x+8=3x
10x-3x=8
7x=8
x=8/7
Hope it helps
Please answer quickly
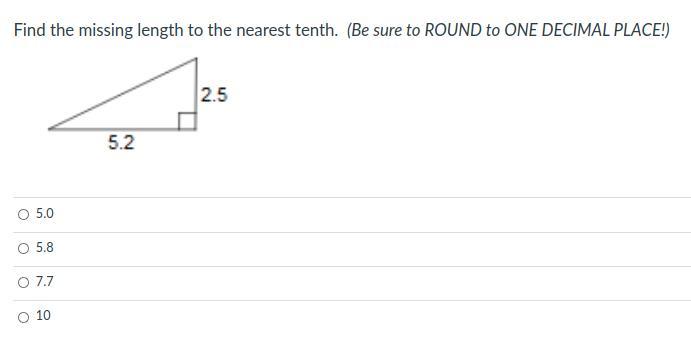
Answers
Answer:
5.8
Step-by-step explanation:
2.5² + 5.2² = c² ≈ 5.8 units
Answer:
5.8
Step-by-step explanation:
√(2.5^2 + 5.2^2) = 5.77
5.77 to the nearest ones decimal point is 5.8
if you multiply 5 and then blank and it equals 565 what the missing number?
Answers
PLEASE HELP ME OUT I DONT UNDERSTAND

Answers
Answer:
(b) and (c)
Step-by-step explanation:
When the equation of a line is given in slope-intercept form (\(y=mx+b\)), m represents the slope of the line and b represents the y-intercept. As we can see, the two lines given have the same slope (-3), but different y-intercepts (the first line has a y-intercept of 4 and the second line has a y-intercept of -11).
Since the slopes of the two lines are the same, they will be parallel, and since their y-intercepts are different, they will not be the same line. Therefore, the two lines will not intersect (a solution to the system is any point where the two lines do intersect), and there is no solution to the system.
As a general rule:
If two lines have different slopes, there will be exactly one solution to the system (the lines will not be parallel and will intersect at exactly one place)If two lines have the same slope, and the same y-intercept, there will be infinitely many solutions (the two lines will be the same, and any point on the line will be a solution)If two lines have the same slope, but different y-intercepts, they will be parallel and will never intersect, so there will be no solution.
Write equation and solve for value of X
(2 questions)
Fairly simple I just can’t seem to remember for finals thank you!

Answers
31) x = 25 degrees
Equation: (2x+15) + x + 90 = 180 degrees
--> 3x+105 = 180
-------> 3x = 75
-------------> x = 25 degrees
32) x = 17 degrees
Equation: (x+52) + (3x+21) + 39 = 180 degrees
--> 4x+112 = 180
-------> 4x = 68
-------------> x = 17 degrees
use a table of laplace transforms to find the laplace transform of the given function. h(t) = 3 sinh(2t) 8 cosh(2t) 6 sin(3t), for t > 0
Answers
The Laplace transform of h(t) is \(L{h(t)} = (6 + 8s)/(s^2 - 4) + 18/(s^2 + 9)\)
To use the table of Laplace transforms, we need to express the given function in terms of functions whose Laplace transforms are known. Recall that:
The Laplace transform of sinh(at) is \(a/(s^2 - a^2)\)
The Laplace transform of cosh(at) is \(s/(s^2 - a^2)\)
The Laplace transform of sin(bt) is \(b/(s^2 + b^2)\)
Using these formulas, we can write:
\(h(t) = 3 sinh(2t) + 8 cosh(2t) + 6 sin(3t)\\= 3(2/s^2 - 2^2) + 8(s/s^2 - 2^2) + 6(3/(s^2 + 3^2))\)
To find the Laplace transform of h(t), we need to take the Laplace transform of each term separately, using the table of Laplace transforms. We get:
\(L{h(t)} = 3 L{sinh(2t)} + 8 L{cosh(2t)} + 6 L{sin(3t)}\\= 3(2/(s^2 - 2^2)) + 8(s/(s^2 - 2^2)) + 6(3/(s^2 + 3^2))\\= 6/(s^2 - 4) + 8s/(s^2 - 4) + 18/(s^2 + 9)\\= (6 + 8s)/(s^2 - 4) + 18/(s^2 + 9)\)
Therefore, the Laplace transform of h(t) is:
\(L{h(t)} = (6 + 8s)/(s^2 - 4) + 18/(s^2 + 9)\)
for such more question on Laplace transform
https://brainly.com/question/30401252
#SPJ11
To find the Laplace transform of h(t) = 3 sinh(2t) 8 cosh(2t) 6 sin(3t), for t > 0, we can use the table of Laplace transforms. The Laplace transform of the given function h(t) is: L{h(t)} = (6/(s^2 - 4)) + (8s/(s^2 - 4)) + (18/(s^2 + 9))
First, we need to use the following formulas from the table:
- Laplace transform of sinh(at) = a/(s^2 - a^2)
- Laplace transform of cosh(at) = s/(s^2 - a^2)
- Laplace transform of sin(bt) = b/(s^2 + b^2)
Using these formulas, we can find the Laplace transform of each term in h(t):
- Laplace transform of 3 sinh(2t) = 3/(s^2 - 4)
- Laplace transform of 8 cosh(2t) = 8s/(s^2 - 4)
- Laplace transform of 6 sin(3t) = 6/(s^2 + 9)
To find the Laplace transform of h(t), we can add these three terms together:
L{h(t)} = L{3 sinh(2t)} + L{8 cosh(2t)} + L{6 sin(3t)}
= 3/(s^2 - 4) + 8s/(s^2 - 4) + 6/(s^2 + 9)
= (3 + 8s)/(s^2 - 4) + 6/(s^2 + 9)
Therefore, the Laplace transform of h(t) is (3 + 8s)/(s^2 - 4) + 6/(s^2 + 9).
To use a table of Laplace transforms to find the Laplace transform of the given function h(t) = 3 sinh(2t) + 8 cosh(2t) + 6 sin(3t) for t > 0, we'll break down the function into its components and use the standard Laplace transform formulas.
1. Laplace transform of 3 sinh(2t): L{3 sinh(2t)} = 3 * L{sinh(2t)} = 3 * (2/(s^2 - 4))
2. Laplace transform of 8 cosh(2t): L{8 cosh(2t)} = 8 * L{cosh(2t)} = 8 * (s/(s^2 - 4))
3. Laplace transform of 6 sin(3t): L{6 sin(3t)} = 6 * L{sin(3t)} = 6 * (3/(s^2 + 9))
Now, we can add the results of the individual Laplace transforms:
L{h(t)} = 3 * (2/(s^2 - 4)) + 8 * (s/(s^2 - 4)) + 6 * (3/(s^2 + 9))
So, the Laplace transform of the given function h(t) is:
L{h(t)} = (6/(s^2 - 4)) + (8s/(s^2 - 4)) + (18/(s^2 + 9))
Learn more about Laplace at: brainly.com/question/31481915
#SPJ11
Find the value of x with angles t=88 degrees a=145 degrees c=137 degrees s=130 degrees r=125degrees and m= x degrees
Answers
To find the value of x, we can use the fact that the sum of angles in a triangle is 180 degrees. Therefore, we can add up the given angles and subtract the sum from 180 degrees to find the value of x.
Sum of angles = t + a + c + s + r + m
180 degrees = 88 degrees + 145 degrees + 137 degrees + 130 degrees + 125 degrees + x degrees
Simplifying the equation:
180 degrees = 625 degrees + x degrees
To isolate x, we can subtract 625 degrees from both sides of the equation:
x degrees = 180 degrees - 625 degrees
x degrees = -445 degrees
Therefore, the value of x is -445 degrees.
Learn more about angles here: brainly.com/question/13954458
#SPJ11
Alex wants to fence in an area for a dog park. He has plotted three sides of the fenced area at the points E (3, 5), F (6, 5), and G (9, 1). He has 22 units of fencing. Where could Alex place point H so that he does not have to buy more fencing?.
Answers
Alex could place point H very close to one of the existing points (E, F, or G) such that the sum of lengths of EH, HF, and FG, should not exceed 22 - 15.21 = 6.79 units.
We have,
Given points:
E (3, 5)
F (6, 5)
G (9, 1)
We'll calculate the distances between these points to determine the perimeter of the fenced area:
\(Distance~ EF: \sqr((x_F - x_E)^2 + (y_F - y_E)^2)\\Distance ~FG: \sqrt((x_G - x_F)^2 + (y_G - y_F)^2)\\Distance ~GE: \sqrt((x_E - x_G)^2 + (y_E - y_G)^2)\)
Calculate the distances:
Distance EF: √((6 - 3)² + (5 - 5)²) = 3 units
Distance FG: √((9 - 6)² + (1 - 5)²) = √(9 + 16) = 5 units
Distance GE: √((3 - 9)² + (5 - 1)²) = √(36 + 16) = 2√13 units
Now, the total perimeter of the current fenced area is:
Perimeter = EF + FG + GE = 3 + 5 + 2√13 ≈ 8 + 7.21 ≈ 15.21 units.
Now, since you have 22 units of fencing available, the maximum additional length for the fourth side, which is the sum of lengths of EH, HF, and FG, should not exceed 22 - 15.21 = 6.79 units.
Thus,
Alex could place point H very close to one of the existing points (E, F, or G) such that the sum of lengths of EH, HF, and FG, should not exceed 22 - 15.21 = 6.79 units.
Learn more about the distance of a line here:
https://brainly.com/question/14645718
#SPJ12
Alex has used 8 units of fencing to enclose his plot from E to F to G, leaving him with 14 units to return from G to the final corner point H. Any point H must be within 14 units of G. H could be (9, -13) which is 14 units below G.
Explanation:Alex can use the distance formula to calculate the distance between the points and see how much fencing he has already used. The distance between points E and F is 3 units (6 - 3 = 3). The distance between points F and G is 5 units (Square root of ((6 - 9)^2 + (5 - 1)^2)). This equates to 8 units of fencing already used. Therefore, Alex has 14 units of fencing left (22 - 8 = 14). To not require any additional fencing, any point H he chooses must be within 14 units of point G. Corner point H could be (9, -13), for example, which is exactly 14 units below G, so it would work perfectly. Alex cannot, however, return to point E (3, 5), because that's farther than 14 units.
Learn more about Distance formula here:https://brainly.com/question/11231122
#SPJ12
I need help
9/2 x 1/4
Answers
Answer:
1 1/8
Step-by-step explanation:
Answer:
1 1/8
Step-by-step explanation:
Consider the following regression model: Y₁ =B₁ + B₂X₂1+ B3X31 + B₂X41 +14₁ Using the model above show that the maximum likelihood estimator for the variance, var (uiX21-X31-B4X4), is biased (be sure to comment of the nature of the bias).
Answers
The maximum likelihood estimator for the variance, (ui|\(X_{2i}\), \(X_{3i}\), β₄\(X_{4i}\)), is unbiased.
To analyze the bias of the maximum likelihood estimator (MLE) for the variance, we need to consider the assumptions and properties of the regression model.
In the given regression model:
\(Y_i\) = β₁ + β₂\(X_{2i}\) + β₃\(X_{3i}\) + β₄\(X_{4i}\) + U\(_{i}\)
Here, \(Y_i\) represents the dependent variable, \(X_{2i}, X_{3i},\) and \(X_{4i}\) are the independent variables, β₁, β₂, β₃, and β₄ are the coefficients, U\(_{i}\) is the error term, and i represents the observation index.
The assumption of the classical linear regression model states that the error term, U\(_{i}\), follows a normal distribution with zero mean and constant variance (σ²).
Let's denote the variance as Var(U\(_{i}\)) = σ².
The maximum likelihood estimator (MLE) for the variance, σ², in a simple linear regression model is given by:
σ² = (1 / n) × Σ[( \(Y_i\) - β₁ - β₂\(X_{2i}\) - β₃\(X_{3i}\) - β₄\(X_{4i}\))²]
To determine the bias of this estimator, we need to compare its expected value (E[σ²]) to the true value of the variance (σ²). If E[σ²] ≠ σ², then the estimator is biased.
Taking the expectation (E) of the MLE for the variance:
E[σ²] = E[ (1 / n) × Σ[( \(Y_i\) - β₁ - β₂\(X_{2i}\) - β₃\(X_{3i}\) - β₄\(X_{4i}\))²]
Now, let's break down the expression inside the expectation:
[( \(Y_i\) - β₁ - β₂\(X_{2i}\) - β₃\(X_{3i}\) - β₄\(X_{4i}\))²]
= [ (β₁ - β₁) + (β₂\(X_{2i}\) - β₂\(X_{2i}\)) + (β₃\(X_{3i}\) - β₃\(X_{3i}\)) + (β₄\(X_{4i}\) - β₄\(X_{4i}\)) + \(U_{i}\)]²
= \(U_{i}\)²
Since the error term, \(U_{i}\), follows a normal distribution with zero mean and constant variance (σ²), the squared error term \(U_{i}\)² follows a chi-squared distribution with one degree of freedom (χ²(1)).
Therefore, we can rewrite the expectation as:
E[σ²] = E[ (1 / n) × Σ[\(U_{i}\)²] ]
= (1 / n) × Σ[ E[\(U_{i}\)²] ]
= (1 / n) × Σ[ Var( \(U_{i}\)) + E[\(U_{i}\)²] ]
= (1 / n) × Σ[ σ² + 0 ] (since E[ \(U_{i}\)] = 0)
Simplifying further:
E[σ²] = (1 / n) × n × σ²
= σ²
From the above derivation, we see that the expected value of the MLE for the variance, E[σ²], is equal to the true value of the variance, σ². Hence, the MLE for the variance in this regression model is unbiased.
Therefore, the maximum likelihood estimator for the variance, (ui|\(X_{2i}\), \(X_{3i}\), β₄\(X_{4i}\)), is unbiased.
Learn more about maximum likelihood estimator click;
https://brainly.com/question/32608862
#SPJ4
Lisa is checking out at the bookstore. Each book (b) costs $1.50 and she has a $5 off coupon she can use. She wants to spend $25 or less in the bookstore. How many books can Lisa buy?
Answers
Answer:
20
Step-by-step explanation:
Given:
Lisa is checking out at the bookstore.
Each book (b) costs $1.50 and she has a $5 off coupon she can use.
She wants to spend $25 or less in the bookstore.
Solve:
Since there is a $5 off coupon..
$1.5b - $5.00<=$25.00
$1.5b<= $30.00
$1.5b/1.5 = $30.00/1.5
b=20
Lisa can buy 20 book.
~lenvy~
Please help with the question below
Answers
If a = 3, then 5a = 15. If a = 11⁄2, then a
3.
Answers
The value of the expression a^3 is 3 3/8
How to evaluate the expression?The given parameters can be represented as
If a = 3, then 5a = 15.
Also, we have the value of the variable a to be
a = 1 1/2
Express the value of the variable a as an improper fraction
So, we have
a = 3/2
When a = 1 1/2 or a = 3/2, the value of a³ is calculated using the following formula
a³ = (1 1/2)³ = (3/2)³
Rewrite the formula as
a³ = (3/2)³
Evaluate the exponent in the above equation
So, we have
a³ = (27/8)³
Evaluate the quotient in the above equation
So, we have
a³ = 3 3/8
Hence, the value of the expression a³ is 3 3/8
Read more about expressions at
https://brainly.com/question/723406
#SPJ1
use the venn diagram to compare and contrast the definitions of the linnaean class answers
Answers
The Linnaean class system provides a framework for understanding the diversity of life on Earth by grouping similar organisms together based on shared characteristics.
By comparing and contrasting the definitions of each class, we can see how different groups of animals are related to each other and how they differ in terms of their biological traits.
The Linnaean class system is a way of organizing living things based on shared characteristics. Let's compare and contrast the definitions of the Linnaean classes using a Venn diagram.
First, we have the class Mammalia, which includes all animals that have hair or fur, produce milk to feed their young, and have specialized teeth. This class overlaps with the class Aves, which includes all birds, because some birds have specialized beaks and feathers that are similar to mammalian hair and teeth. However, birds do not produce milk.
Next, we have the class Reptilia, which includes animals that are cold-blooded, lay eggs, and have scales or plates on their skin. This class overlaps with both Mammalia and Aves in terms of species that lay eggs, such as monotremes (platypus and echidnas) and some birds (ostriches and emus). However, reptiles lack specialized teeth and do not produce milk.
Finally, we have the class Amphibia, which includes animals that are cold-blooded, breathe through their skin, and undergo metamorphosis from a water-dwelling larval stage to a land-dwelling adult stage. This class overlaps with Reptilia in terms of some shared characteristics, but Amphibia also lacks specialized teeth and does not lay eggs with hard shells like reptiles.
More on Linnaean class system: https://brainly.com/question/2548027
#SPJ11
Help! My teacher never taught me this and gave it to me for what ever reason. Questions 6-11. (Middle school)

Answers
Answer:
6. 12cm
7. 11.2 cm
8. 92 degrees
9. 53 degrees
10. 37.5 cm
11. $ 693.12
Step-by-step explanation:
For questions 6-9 the triangle is congurent which means both their angles will be equal.
For the sides you can see that the second triangle is 1.5 times smaller than the first one as taking one of the sides 21/14= 1.5
So for Q. 6 we can multiply side PQ by 1.5.
For Q.7 divide CA by 1.5.
For Q. 10 we can do cross multiplication:
5/4 = x/30
= 150= 4x
= 37.5=x
For Q 11 we can see the size of the paper is 1.9 times bigger than the original one (38/20)
So the shorter side is 30.4 cm.
Then we have to find the area of the paper to multiply the two dimensions and we get 1155.2 square inches.
Then to figure out the money we multiply again and we get $693.12.
for x = 3 and y = 4: b. x2 + y
Answers
Answer:
10
Step-by-step explanation:
substitute the variables with their numbers
X2+Y
(3)2 +(4)
3x2=6
6+4
10
Which of the following equations is equivalent to 5 / 8 = 22 / x - 6?
5x – 30 = 176
5x – 3 = 176
40 = 30x – 132
100 = 8x – 48
Answers
Answer:
5x – 30 = 176
Step-by-step explanation:
Help with problem in photo!

Answers
Check the picture below.
\(4+10x=\cfrac{(9x+20)+10x}{2}\implies 8+20x=19x+20\implies x=12 \\\\[-0.35em] ~\dotfill\\\\ 4+10x\implies 4+10(12)\implies \stackrel{ \measuredangle DEC }{124^o}\)

Consider the following data drawn independently from normally distributed populations: (You may find it useful to appropriate table: z table or t table)
xˉ1 = −17.1
s1^2 = 8.4
n1=22
xˉ2 = −16.0
s2^2 = 8.7
n2 = 24
a. Construct the 90% confidence interval for the difference between the population means. Assume the population va unknown but equal. (Round final answers to 2 decimal places.)
confidence interval is __ to __
Answers
The 90% confidence interval for the difference in the population means is -2.51 to 0.31
Calculating the 90% confidence interval for the population mean differenceFrom the question, we have the following parameters that can be used in our computation:
xˉ₁ = −17.1
s₁² = 8.4
n₁ = 22
xˉ₂ = −16.0
s₂² = 8.7
n₂ = 24
Calculate the pooled variance using
P = (df₁ * s₁² + df₂ * s₂²)/df
Where
df₁ = 22 - 1 = 21
df₂ = 24 - 1 = 23
df = 22 + 24 - 2 = 44
So, we have
P = (21 * 8.4 + 23 * 8.7)/44
P = 8.56
Also, we have the standard error to be
SE = √(P/n₁ + P/n₂)
So, we have
SE = √(8.56/22 + 8.56/24)
SE = 0.86
The z score at 90% CI is 1.645, and the CI is calculated as
CI = (x₁ - x₂) ± z * SE
So, we have
CI = (-17.1 + 16.0) ± 1.645 * 0.86
This gives
CI = -1.1 ± 1.41
Expand and evaluate
CI = (-2.51, 0.31)
Hence, the confidence interval is -2.51 to 0.31
Read more about confidence interval at
https://brainly.com/question/15712887
#SPJ1
A regular polygon has 16 sides. If one of its angles measures (5h − 29)°, what is the value of h?
PLEASE I NEED HELP!!
Answers
Each angle in a regular polygon is 180(n-2)/n
We know n = 16 so each angle is 180 x 14 / 16
5h - 29 = 180 x 14 / 16
Multiplying both sides by 16 gives
80h - 464 = 2520
80h = 2056
h = 2056 / 80 =25.7
I don’t get it honestly

Answers
Answer:
C
Step-by-step explanation:
Work out the size of angle x.

Answers
Answer:
x = 46°
Step-by-step explanation:
Angles on a straight line sum to 180°.
Therefore, the interior angle of the triangle that forms a linear pair with the exterior angle marked 130° is:
⇒ 180° - 130° = 50°
The interior angle of the triangle that forms a linear pair with the exterior angle marked 96° is:
⇒ 180° - 96° = 84°
The interior angles of a triangle sum to 180°. Therefore:
⇒ 50° + 84° + x = 180°
⇒ 134° + x = 180°
⇒ 134° + x - 134° = 180° - 134°
⇒ x = 46°
Therefore, the size of angle x is 46°.

for what values of x does 5x^2+4x-4=0
Answers
Answer: See explanation
Step-by-step explanation:
x=-(2-2*the square root of 6)/5, about 0.58
or
x=-(2+2*the square root of 6)/5, about -1.38
The values of the x from equation \(5x^2+4x-4=0\) are x = 0.5798 and -1.38.
Given that:
Equation: \(5x^2+4x-4=0\)
To find the values of x that satisfy the equation \(5x^2+4x-4=0\), use the quadratic formula:
\(x = \dfrac{ -b \± \sqrt{b^2 - 4ac}}{ 2a}\)
Compare the equation with \(ax^2 + bx + c = 0\).
Here, a = 5, b = 4, and c = -4.
Plugging in the values to get,
\(x = \dfrac{-4 \± \sqrt{4^2 - 4 \times 5 \times (-4)}}{2 \times 5} \\x = \dfrac{-4 \± \sqrt{16 +80}}{10} \\x = \dfrac{-4 \± \sqrt{96}}{10}\\x = \dfrac{-4 \± {4\sqrt6}}{10}\)
So the solutions for x are calculates as:
Taking positive sign,
\(x = \dfrac{-4 + {4\sqrt6}}{10}\\x = \dfrac{-4 + {9.798}}{10}\\\)
x = 5.798/10
x = 0.5798
Taking negative sign,
\(x = \dfrac{-4 - {4\sqrt6}}{10}\\x = \dfrac{-4 - {9.798}}{10}\\\)
x = -13.798/10
x = -1.38
Hence, the exact solutions for the equation \(5x^2 + 4x - 4 = 0\) are x = 0.5798 and -1.38.
Learn more about Quadratic formula here:
https://brainly.com/question/22364785
#SPJ4
A number decreased by 9 is 12. Which equation represents this situation?
Answers
Answer:
x - 9 = 12
Step-by-step explanation:
We can use x as "a number"
So the equation so far is just "a number", or x.
Decreased by 9 can also be said as subtracted by 9, so that makes the equation x - 9.
"is 12" can also be said as equals 12, which makes the equation x - 9 = 12
Answer:
_ - 9 = 12
Step-by-step explanation:
You can identify the starting number by adding 9 and 12 together to get 21. The completed equation would be 21 - 9 = 12.
a class has 12 boys and 4 girls. if three students are selected at random from the class, the probability that they are all boys is
Answers
The probability that all three selected students are boys is approximately 0.3929 or 39.29%.
To calculate the probability that all three selected students are boys, we need to consider the total number of possible outcomes and the number of favorable outcomes.
In this case, there are 12 boys and 4 girls in the class, making a total of 16 students. We want to select three students, and we want all three of them to be boys.
The total number of ways to select three students from the class is given by the combination formula, which can be represented as:
Total Possible Outcomes = nCr(16, 3) = (16!)/((16-3)! * 3!) = 560
Now, let's consider the number of favorable outcomes where all three selected students are boys. Since there are 12 boys, we can choose three of them using the combination formula:
Favorable Outcomes = nCr(12, 3) = (12!)/((12-3)! * 3!) = 220
Therefore, the probability that all three selected students are boys is:
Probability = Favorable Outcomes / Total Possible Outcomes = 220 / 560 ≈ 0.3929, or approximately 39.29%.
Hence, the probability that all three selected students are boys is approximately 0.3929 or 39.29%.
learn more about probability here
https://brainly.com/question/32117953
#SPJ11
Jeremiah created a game where he flips a fair coin 3 times. Jeremiah wins the game if he flips heads at least 2 times. What are all the possible outcomes to win, based on the first two flips? What is the probability of winning, based on the first two flips? Move words and fractions to the table to answer the questions.

Answers
The Probability of winning based on the first two flips is:P(win) = P(X = 2) + P(X = 1) = 1/4 + 1/2 = 3/4The probability of winning is 3/4.
Jeremiah created a game where he flips a fair coin 3 times. Jeremiah wins the game if he flips heads at least 2 times. What are all the possible outcomes to win, based on the first two flips
The possible outcomes to win the game, based on the first two flips, are:
Head, Head (HH)Head, Tail (HT)Tail, Head (TH)The only possible outcome that does not lead to a win is Tail, Tail (TT).
What is the probability of winning, based on the first two flips
The probability of winning, based on the first two flips, can be calculated using the binomial distribution formula:P(X = k) = nCk * pk * (1-p)n-k
Where :n = 2 (since we are considering the first two flips)k = 2 or 1 (since we need at least 2 heads to win)P(head) = p = 1/2P(tail) = 1 - p = 1/2
Substituting the values in the formula:
P(X = 2) = 2C2 * (1/2)2 * (1/2)0 = 1 * 1/4 * 1 = 1/4P(X = 1) = 2C1 * (1/2)1 * (1/2)1 = 2 * 1/2 * 1/2 = 1/2
Therefore, the probability of winning based on the first two flips is:P(win) = P(X = 2) + P(X = 1) = 1/4 + 1/2 = 3/4The probability of winning is 3/4.
For more questions on Probability .
https://brainly.com/question/30390037
#SPJ8
PLEASE help
Allen mixes 1 cup of water that is 150°F and 1 cup of cold chicken broth that is 50°F. The end temperature of the mixture would be about___________
. Chris combines 2 cups of soup that is 50°F with 1 cup of water that is 150°F. The end temperature of the mixture would be ______
Answers
Answer:
1) 100 degrees F
2) 50 degrees F
Step-by-step explanation:
its just simple subtraction
Please help due in 20 mins

Answers
Answer:
1. -.005
2.-1/2
3. 0
4. 2
Step-by-step explanation:
if it is negative put positive and if it is positive put negative. for 0 it will always stay the same
7j+8s=455 what do j and s equal?
Answers
Answer:
\( \sf \: j= \frac{−8}{7}s+ \frac{445}{7} , \sf \: s= \frac{−7}{8}j+ \frac{445}{8} \)
Step-by-step explanation:
\( \sf \: Let's solve for j. \\ \sf \: 7j+8s=445 \\ \sf \: Step 1: \: Add \: -8s \: to \: both \: s ides. \\ \sf \: 7j+8s+−8s=445+−8s \\ \sf \: 7j=−8s+445 \\ \sf \: Step \: 2: \: Divide \: both \: sides \: by \:7. \\ \sf \frac{7j}{7}= \frac{−8s+445}{7} \\ \sf \: j= \frac{−8}{7}s+ \frac{445}{7} \\\)